Efecto motivo y dimensionalidad

En la sección dedicada a la cadena monoatómica resolvíamos la ecuación de los modos normales de vibraciones en un sólido,

(428)\[K_k\vec{\epsilon}= M\omega_k^2 \vec{\epsilon}.\]

de forma muy sencilla, ya que tan sólo había un grado de libertad en la celda unidad (había un átomo que se podía mover a lo largo de un único eje). En esta sección vamos a discutir que ocurre cuando el sólido tiene más grados de libertad. Estos pueden provenir de dos fuentes bien diferenciadas; por un lado el cristal puede tener más de un átomo de motivo y, por otro, los átomos pueden moverse en más de una dimensión. Trabajaremos cada uno de estos casos por separado en las próximas secciones.

A partir de este momento es muy importante tener en cuenta el número de grados de libertad del sistema que coincide con el tamaño del vector \(\vec{\varepsilon}\), que describe las amplitudes de los diferentes modos y cuya dimensión es es \(N_{uc}\times D\), donde \(N_{uc}\) es el número de átomos en la celda unidad y D es la dimensión del sistema. Este valor, como veremos más abajo, es también el número de bandas vibracionales que tiene el sistema.

¿Celda primitiva o celda convencional?

Si se considera un sistema donde la celda convencional no coincide con la primitiva debemos recordar que la celda primitiva es la más pequeña que contiene toda la información del sistema y que, por tanto, debemos utilizar la misma para no repetir información. Es decir, si estudiamos el silicio, que tiene una celda de tipo F que contiene 8 átomos, deberemos buscar la celda primitiva que contiene, tan sólo 2 átomos y, por tanto, el tamaño del vector \(\vec{\varepsilon}\) será 6, el producto de 2 átomos en la celda unidad y 3, que son las direcciones en las que se pueden mover los átomos.

Motivo

Veamos primero que ocurre si nuestro cristal tiene más de un átomo de motivo. Observando la ecuación que describe los modos, Ec. (428), tenemos que el vector que describe las amplitudes de las vibraciones, \(\vec{\varepsilon}\), no será un escalar, si no que, ahora que consideramos una cadena lineal diatómica (ver Fig. 242), donde hay 2 átomos por celda unidad, la dimensión del vector es 2 ya que estos átomos sólo se pueden mover sobre el eje z.

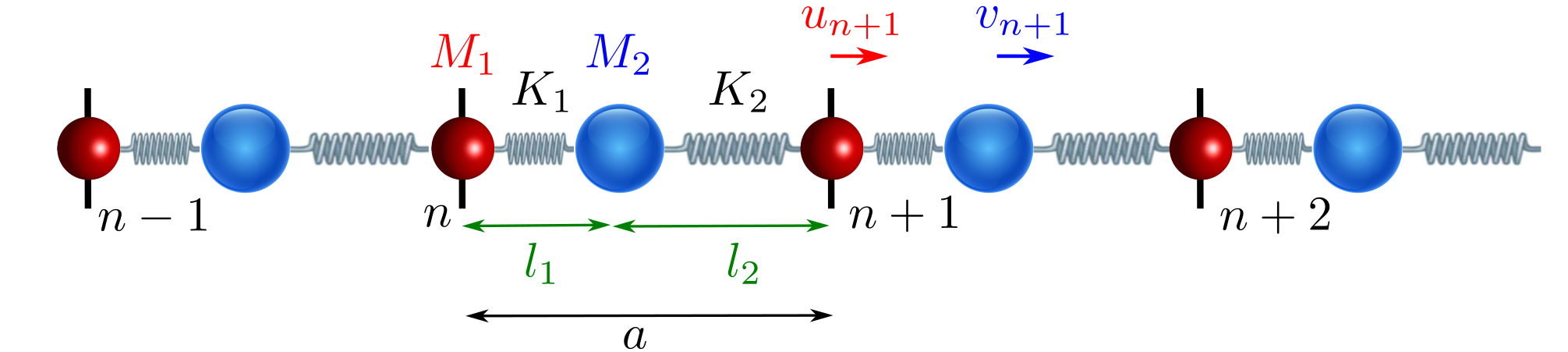
Fig. 242 Ilustración de una cadena diatómica, donde el primer átomo se representa por una esfera roja y el otro por una azul. La masa y el desplazamiento del átomo rojo se representan, respectivamente, por \(M_1\) y \(u_n\), mientras que las del azul son, \(M_2\) y \(v_n\). Nótese que ahora hay 2 enlaces bien diferenciados (y dos valores de las constantes de fuerza a primeros vecinos) que se corresponden con la interacción de un átomo rojo con uno azul a su izquierda y a su derecha, respectivamente.

Podemos concentrar el movimiento de los dos átomos en un único vector, \(\vec{u}\),

(429)\[\begin{split} \vec{u}=\begin{pmatrix} u_n\\v_n \end{pmatrix}\end{split}\]

donde al desplazamiento del primer átomo de la celda n, por claridad, lo llamamos \(u_n\) y al del segundo \(v_n\) (ver Fig. 242. Supondremos que los dos átomos de la celda tienen masas diferentes, \(M_1\) (átomo rojo) y \(M_2\) (átomo azul). Dado que el origen de la celda es arbitrario podemos situarlo, por ejemplo, sobre el átomo rojo. Es importante darse cuenta que el átomo azul puede situarse en cualquier punto de la celda, no necesariamente en su centro, lo que crea interesantes situaciones físicas que se discutirán a continuación.

Energía elástica

Utilizando la Fig. 242 podemos ahora calcular la energía elástica del sólido. Para ello sumaremos las interacciones elásticas que hay en cada celda, indicada por un índice n. En particular, vemos que dentro de la celda n tenemos dos muelles diferentes. El primero, moviéndonos de izquierda a derecha, une un átomo rojo con uno azul, y tiene una rigidez dada por la constante de fuerza \(K_1\). El segundo, también moviéndonos de izquierda a derecha une al átomo azul en la celda n con el átomo rojo en la celda n+1. En este caso la constante de fuerza es \(K_2\). Por tanto, la energía elástica del sólido es,

(430)\[ U=\sum_n \left[ \frac{1}{2}K_1 \left(v_n-u_n\right)^2+ \frac{1}{2}K_2 \left(u_{n+1}-v_n\right)^2 \right]\]

Aunque estos dos muelles representen enlaces entre un átomo rojo y otro azul pueden ser diferentes ya que debido a las posiciones de estos átomos dentro de la celda las distancias relativas asociadas al primer y segundo muelle pueden ser diferentes. Por ejemplo, en la Fig. 242 la distancia entre el átomo rojo y azul a través del primer muelle, \(l_1\), es más pequeña que a través del segundo, \(l_2\). Esto sugiere que \(K_1>K_2\).

Ecuación del movimiento

Ahora escribimos las ecuaciones del movimiento para cada uno de los átomos, teniendo cuidado de tener en cuenta todos los muelles en los que participa cada uno de los átomos. El resultado es el siguiente,

(431)\[M_1 \frac{d^2 u_n}{dt^2} = -\frac{\partial U}{\partial u_n} = -K_1 v_n -K_2 v_{n-1} + (K_1+K_2) u_n\]

(432)\[M_2 \frac{d^2 v_n}{dt^2} = -\frac{\partial U}{\partial v_n} = -K_1 u_n -K_2 u_{n+1} + (K_1+K_2) v_n\]

Solución de la ecuación del movimiento

Para encontrar la solución de las Ecs. (431)-(432) recordamos el teorema de Bloch y escribimos, teniendo en cuenta que, claramente, la amplitud del átomo 1 y del 2 no son, en general, las mismas,

(433)\[\begin{split}\begin{pmatrix} u_n\\v_n \end{pmatrix}=\begin{pmatrix}\epsilon_u\\ \epsilon_v\end{pmatrix} e^{i(kna-\omega_kt)}=\vec{\epsilon}e^{i(kna-\omega_kt)}\end{split}\]

Ahora sustituímos la Ec. (433) en las Ecs. (431)-(432),

(434)\[\begin{split}\begin{pmatrix} u_n\\v_n \end{pmatrix}=\begin{pmatrix} \epsilon_u\\\epsilon_v \end{pmatrix}e^{i(kna-\omega_kt)}\rightarrow \begin{cases} M_1 \frac{d^2 u_n}{dt^2} &= -K_1 v_n -K_2 v_{n-1} + (K_1+K_2) u_n\\ M_2 \frac{d^2 v_n}{dt^2} &= -K_1 u_n -K_2 u_{n+1} + (K_1+K_2) v_n \end{cases}\end{split}\]

Operando encontramos las siguientes ecuaciones,

(435)\[\begin{split}-M_1 \omega_k^2 \epsilon_u &= -K_1 \epsilon_v -K_2e^{-ika} \epsilon_v + (K_1+K_2) \epsilon_u\\ -M_2 \omega_k^2 \epsilon_v & = -K_1 \epsilon_u -K_2e^{ika} \epsilon_u + (K_1+K_2) \epsilon_v\end{split}\]

Si ahora escribimos la Ec. (435) en forma matricial, resulta sencillo identificar que se trata de la Ec. (428).

(436)\[\begin{split}\begin{pmatrix} M_1 & 0\\ 0 & M_2 \end{pmatrix} \omega_k^2 \begin{pmatrix} \epsilon_u\\\epsilon_v \end{pmatrix} = \begin{pmatrix} -(K_1+K_2) & K_1+K_2e^{-ika} \\ K_1+K_2e^{ika} & -(K_1+K_2) \end{pmatrix} \begin{pmatrix} \epsilon_u\\\epsilon_v \end{pmatrix} \rightarrow M\omega_k^2 \vec{\epsilon}=K_k\vec{\epsilon}\end{split}\]

Para resolverla movemos todos los térmicos a la izquierda,

(437)\[\begin{split} \left[\begin{pmatrix} -(K_1+K_2) & K_1+K_2e^{-ika} \\ K_1+K_2e^{ika} & -(K_1+K_2) \end{pmatrix}+ \begin{pmatrix} M_1 & 0\\ 0 & M_2 \end{pmatrix}\omega_k^2 \right]\vec{\epsilon}=\begin{pmatrix} 0\\ 0 \end{pmatrix}\end{split}\]

y observamos que, para encontrar \(\varepsilon_u\) y \(\varepsilon_v\), debemos resolver un sistema de ecuaciones homogeneo. Este tiene una solución no trivial sólo si el determinante secular es cero,

(438)\[\begin{split}\left\vert K_k+M\omega_k^2\right\vert = 0 \rightarrow \begin{vmatrix} -(K_1+K_2)+M_1\omega_k^2 & K_1+K_2e^{-ika} \\ K_1+K_2e^{ika} & -(K_1+K_2)+M_2\omega_k^2 \end{vmatrix}=0\end{split}\]

Por lo que, resolviendo el determinante, obtenemos una ecuación bicuadrática en \(\omega_k\),

(439)\[M_1 M_2 \omega_k^4-(K_1+K_2)(M_1+M_1)\omega_k^2+2K_1 K_2 (1-\cos ka) =0\]

cuya solución es:

(440)\[\omega_k^2 = \frac{(K_1+K_2)(M_1+M_1)\pm\sqrt{(K_1+K_2)^2(M_1+M_1)^2-8M_1 M_2 K_1 K_2 (1-\cos ka)}}{2M_1 M_2}\]

Representando estas curvas en la primera zona de Brillouin obtenemos el diagrama que se muestra el Fig. 243. Aquí tenemos una curva inferior que se denomina banda acústica y otra superior que se denomina banda óptica por motivos que se describirán seguidamente.

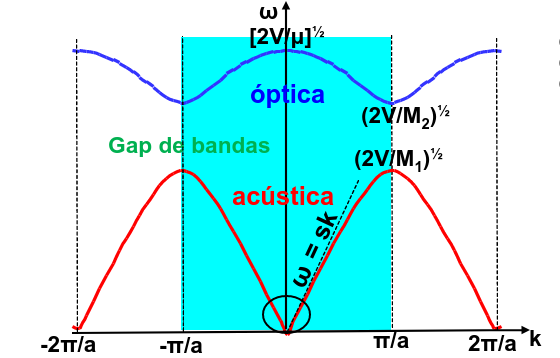
Fig. 243 Representación de las bandas vibracionales en la cadena diatómica dentro de la primera zona de Brillouin (mostrada por un fondo oscuro). La banda inferior, en rojo, se denomina acúsitica y la superior, en azul, es óptica.

Interpretación de la ecuación de movimento

Tal y como hacíamos en la cadena monoatómica, para interpretar los diferentes modos debemos hacer uso del teorema de Bloch,

(441)\[ T_a u(n)=u(n+1)=\epsilon e^{i(k(n+1)a+\omega_kt)} = e^{ika}\epsilon e^{i(kna+\omega_kt)}=e^{ika} u(n)\]

donde vemos que para \(k=0\) el movimiento en todas las celdas es el mismo mientras que en el borde de zona, \(k=\pi/a\), el movimiento es en contra fase.

El problema surge observando que en la cadena diatómica hay dos átomos en la celda unidad, por lo que va a haber dos bandas vibracionales por punto de la red recíproca y dos modos, que son los autovectores de la Ec. (436).

• Modos en \(k=0\): Tomando la Ec. (436) y haciendo \(k=0\) y \(\omega_k=0\) (una de las soluciones que vemos en la Fig. 243. Obtenemos que,

(442)\[\begin{split}\begin{pmatrix} -(K_1+K_2) & K_1+K_2 \\ K_1+K_2 & -(K_1+K_2) \end{pmatrix} \begin{pmatrix} \epsilon_u\\\epsilon_v \end{pmatrix} =0\end{split}\]

de donde es sencillo ver que la solución es que \(\varepsilon_u=\varepsilon_v\), es decir, que el primer átomo y el segundo se mueven en fase lo mismo (ver Fig. 244. Como ya conocemos un desplazamiento rígido de la red da no cambia la energía elástica y, por tanto, la frecuencia asociado al mismo es nula.

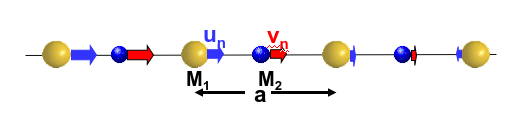
Fig. 244 Representación del modo acústico cercano a \(k=0\) en una cadena diatómica. Los átomos se mueven prácticamente en fase por lo que sus frecuencias son bajas.

Por otro lado, el segundo autovector tiene que ser ortogonal al primero, por lo que en el movimiento resultante es de los átomos de la celda unidad se mueven en oposición de fase (ver Fig. 245). Este modo es, claramente, el de más alta energía dado que contrae y expande los enlaces de forma máxima. Esto es, precisamente, lo que vemos en el diagrama de bandas (Fig. 243).

Fig. 245 Representación del modo acústico óptico cercano a \(k=0\) en una cadena diatómica. Los átomos se mueven prácticamente en contrafase por lo que sus frecuencias son altas.

En el diagrama de bandas, Fig. 243, podemos observar que la dispersión de las bandas en la parte inferior es lineal, lo que permite definir la velocidad del sonido, \(s=d\omega_k/d k\), como la velocidad de grupo de la onda. Por ello, las bandas que tienden a frecuencia nula, \(\omega_k\rightarrow 0\), alrededor de k=0 se denominan bandas acústicas. Por otro lado, las bandas que no son acústicas suelen tener frecuencias más altas, a veces llegando al óptico, y se denominan bandas ópticas.

Todos los sistemas tienen un número de bandas acústicas igual al número de dimensiones en las que se pueden mover los átomos. Esto es lógico ya que podemos mover la red de forma rígida a lo largo de esas dimensiones y no cambiar su energía. Por otro lado, el número de bandas ópticas es el resto, es decir, \(N_{uc}\times D - D = D (N_{uc}-1)\).

• Modos en \(k=\pi/a\): Si ahora se encuentran los autovectores asociados al borde de zona tenemos que los movimientos se corresponden con desplazamientos del átomo 1 y del átomo 2 por separado (ver Fig. 246, y Fig. 247).

Fig. 246 Representación del modo acústico de la cadena diatómica cerca del borde de zona, \(k\approx \pm \pi/a\),. Los movimientos son, principalmente los del átomo más pesado.

Fig. 247 Representación del modo óptico de la cadena diatómica cerca del borde de zona, \(k\approx\pm \pi/a\),. Los movimientos son, principalmente, los del átomo más ligero.

Dimensionalidad

Veamos que ocurre ahora cuando los átomos pueden vibrar en diferentes direcciones. Si, por ejemplo, nos imaginamos la cadena monoatómica pero los átomos ahora pueden moverse, también, en direcciones perpendiculares a la cadena tenemos que el vector, \(\vec{\varepsilon}\), tendrá 3 posibles direcciones,

(443)\[\begin{split} \vec{\varepsilon}=\begin{pmatrix} \varepsilon_x\\\varepsilon_y\\\varepsilon_z \end{pmatrix}\end{split}\]

por lo que, al diagonalizar y resolver la Ec. (428) encontraremos 3 autovalores diferentes, es decir, encontraremos 3 bandas vibracionales. Esto es lo que está representado en la Fig. 248.

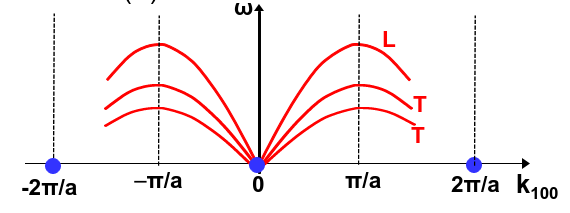
Fig. 248 Ilustración de las bandas vibracionales de la cadena monoatómica donde los átomos pueden moverse en 3 dimensiones. En vez de obtener una única banda longitudinal se obtienen 3, una longitudinal (L) y dos transversales (T).

¿Qué características tienen ahora estas bandas? Como sabemos, las ondas se propagarán en la dirección indicada por su vector de ondas \(\vec{k}\), que en este caso estará sobre el eje z (la única dirección posible en la red recíproca). Ahora el vector \(\vec{\varepsilon}\) tiene dos posibilidades; la primera es que \(\vec{\varepsilon}\) sea paralelo a \(\vec{k}\),

(444)\[\vec{k} \parallel \vec{\epsilon}\]

es decir, vibraciones con los átomos moviéndose en el eje z, como ocurría en la sección anterior. Esto es lo que denominamos una onda longitudinal que se denota en el Fig. 248 con una L.

También es posible que los átomos se muevan en perpendicular a vector de ondas (y la cadena),

(445)\[\vec{k} \perp \vec{\epsilon}\]

esto es lo que llamamos ondas transversales. Dado que la cadena se encuentra a lo largo del eje z estos movimientos tienen 2 posibilidades, el eje x o el eje y (o cualquier combinación lineal de las mismas). Eso significa que habrá 2 bandas transversales en el sistema, tal y como está indicado en el diagrama de bandas, Fig. 248, con una T.

Normalmente esperamos que los modos longitudinales, que tienen que ver con la compresión/elongación de los enlaces sean más energéticas que las transversales, que tienen que ver con movientos perpendiculares a los enlaces y que modifican de forma más débil los mismos. `

Combinación de motivo y dimensionalidad

En caso de trabajar con sistemas con varios átomos de motivo y moviento en 2 o 3 dimensiones todo lo anterior sigue siendo válido. Por ejemplo, el diagrama de bandas, Fig. 249, muestra que ocurre cuando los átomos de la cadena diatómica pueden moverse en 3 dimensiones.

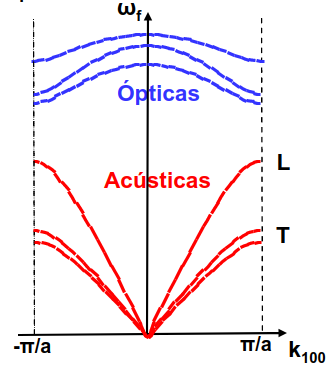
Fig. 249 Ilustración de las bandas vibracionales de la cadena diatómica con vibraciones en 3 dimensiones. Vemos que tanto la banda óptica como la acústica se dividen en una longitudinal y 2 bandas transversales.

Podemos ver que, de un total de 6 bandas (2 átomos por celda unidad y 3 dimensiones de movimiento), hay 3 bandas acústicas, que se corresponden con los desplazamientos a lo largo de los ejes x, y y z, y 3 ópticas.

Si ahora quisieramos describir la red mostrada en la Fig. 250 donde los átomos pueden moverse en el plano de la figura tendríamos que el sistema tiene 2 átomos de motivo (uno azul y otro rojo) y cada uno puede moverse en dos dimensiones (x,y). Por lo tanto, el sistema tiene 4 bandas vibracionales. De estas 2 serán acústicas (2 dimensiones de movimiento posible) y 2 (4 totales - 2 acústicas) serán ópticas.

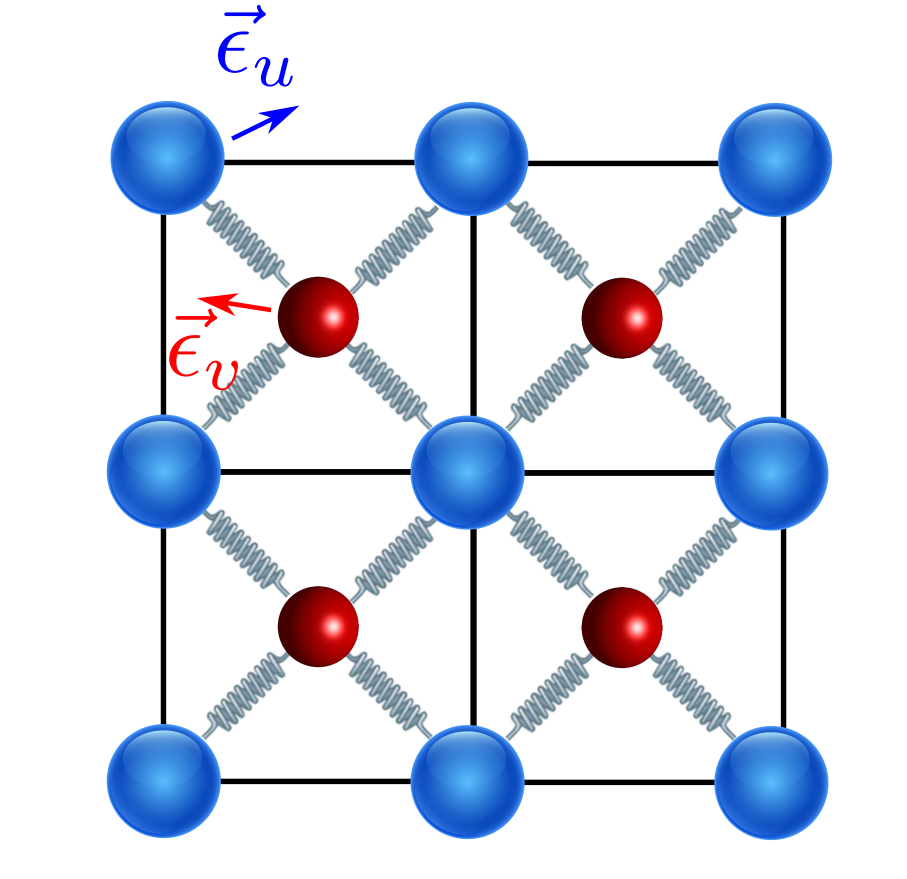
Fig. 250 Ilustración de un sistema sencillo en 2 dimensiones que tiene 2 átomos de motivo. Uno se representa por una esfera azul y otro por una esfera roja. La celda unidad se representa mediante una línea sólida negra.

Si quisieramos definir matemáticamente el vector \(\vec{\varepsilon}\) tendríamos que tener en cuenta que el átomo azul se puede mover a lo largo del eje x e y,

(446)\[\begin{split}\vec{u}_n=\begin{pmatrix} u_n^x\\u_n^y \end{pmatrix}\end{split}\]

y, lo mismo, el átomo rojo,

(447)\[\begin{split}\vec{v}_n=\begin{pmatrix} v_n^x\\v_n^y \end{pmatrix}.\end{split}\]

Por lo tanto, los modos de vibración tendrían la forma,

(448)\[\begin{split}\begin{pmatrix} u_n\\v_n \end{pmatrix}=\begin{pmatrix} \epsilon_u\\\epsilon_v \end{pmatrix}e^{i(kna-\omega_kt)}\rightarrow \begin{pmatrix} \vec{u}_n\\\vec{v}_n \end{pmatrix}=\begin{pmatrix} \epsilon_u^x\\\epsilon_u^y\\\epsilon_v^x\\\epsilon_v^y \end{pmatrix}e^{i(kna-\omega_kt)}.\end{split}\]

Finalmente, en la Fig. 251 se ilustran los movimientos longitudinales y transversales en una red monoatómica al igual que los modos longitudinales y transversales ópticos en una red con dos átomos de motivo.

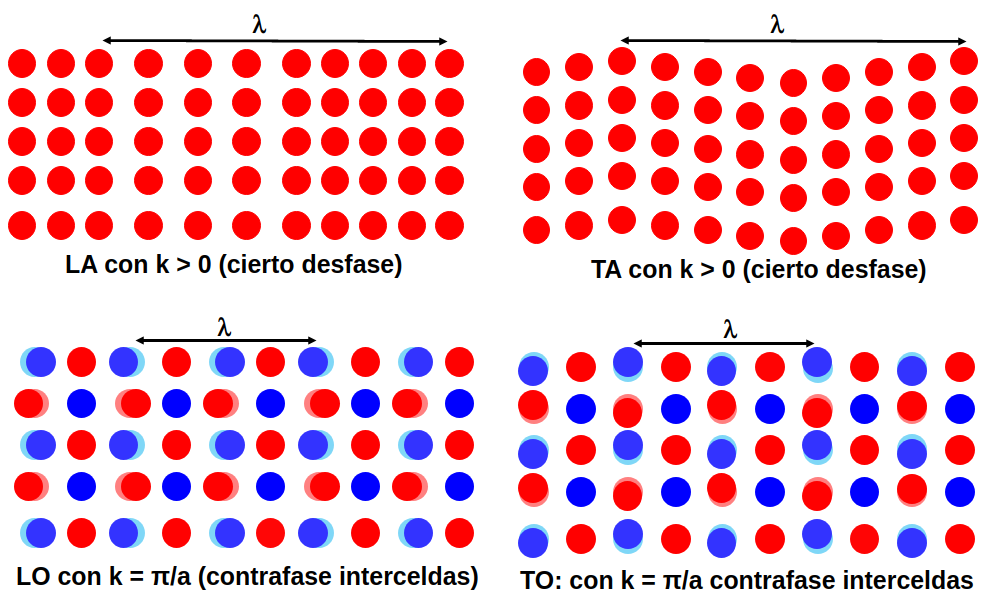
Fig. 251 Ilustración de varios tipos de ondas en sólidos sencillos bidimensionales. En la parte superior se muestran ondas longitudinales (a la izquierda) y transversales (a la derecha) de un sólido con un único átomo de motivo. En la parte inferior se muestra una onda longitudinal óptica, a la izquierda, y otra transversal óptica en un sólido con 2 átomos de motivo (mostrados como círculos de diferente color).

Problems and solution examples