Base de la red recíproca

Base de la red recíproca#

En este apartado vamos a dar las definiciones que necesitaremos para trabajar en el espacio de las frecuencias (realmente momentos o vectores de onda), que es lo que llamamos el espacio recíproco. Vamos a empezar con una definición geométrica, que resultará de gran ayuda cuando intentemos entender las técnicas experimentales de difracción de rayos-X, que son clave para caracterizar los materiales cristalinos. Seguidamente daremos una definición más abstracta que, aún siendo completamente equivalente a la anterior, es muy útil cuando queramos utilizar ondas en cristales. Finalmente, discutiremos la manera en que denotamos coordenadas, tanto en el espacio directo como en el recíproco.

Planos red directa#

Imaginemos que queremos encontrar todos los planos que pasan por los puntos de la red directa. Para definir un plano necesitamos tres puntos de la red o, equivalentemente, dos vectores de la misma (que unen, cada uno, dos puntos de la red) y un punto donde se apoya el plano. Si nos centramos, en un principio, tan sólo en las direcciones que pueden tener estos planos podemos partir de dos vectores no colineales de la red directa,

(51)#\[\vec{R}_1 = u_1 \vec{a}_1 + v_1 \vec{a}_2 + w_1 \vec{a}_3 \]

(52)#\[\vec{R}_2 = u_2 \vec{a}_1 + v_2 \vec{a}_2 + w_2 \vec{a}_3 \]

donde \(u_1\), \(u_2\), \(v_1\), \(v_2\), \(w_1\) y \(w_2\) son número enteros. Tal y como se ilustra en la Fig. 62 el vector director de un plano que contiene a los vectores \(\vec{R}_1\) y \(\vec{R}_2\) es perpendicular a ambos.

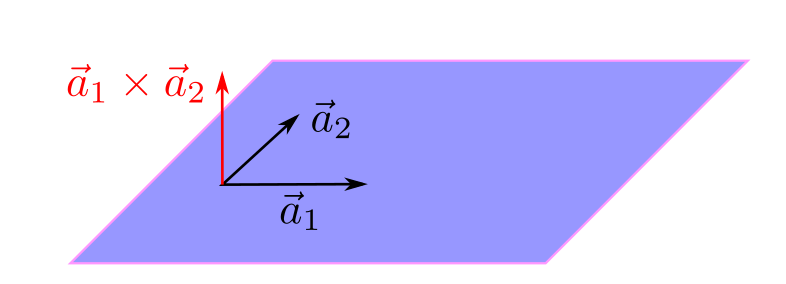
../_images/perpendicular.png — Fig. 62 Dados los vectores \(\vec{a}_1\) y \(\vec{a}_2\), contenidos en el plno, se puede encontrar el vector director del mismo, que es perpendicular a la superficie, mediante el producto vectorial de estos dos vectores.#

Dado que el producto vectorial de dos vectores es perpendicular a ambos, el vector director del plano es paralelo al producto vectorial de \(\vec{R}_1\) y \(\vec{R}_2\). Por ello, podemos expresar, de forma general, que el vector director de un plano que contiene a dos vectores de la red es,

(53)#\[ \vec{R}_1\times \vec{R}_2 = \left(u_1 v_2 - u_2 v_1\right) \vec{a}_1\times\vec{a}_2+ \left(v_1 w_2 - v_2 w_1\right) \vec{a}_2\times\vec{a}_3+ \left(w_1 u_2 - w_2 u_1\right) \vec{a}_3\times\vec{a}_1 \]

En esta última expresión se puede observar que el vector resultante es una combinación lineal de tres vectores, que son las diferentes maneras de combinar los vectores de la base del espacio directo mediante productos vectoriales. El resultado del producto vectorial también es una red de Bravais dado dado que, como podemos observar en la Ec. (53), los coeficientes de los productos de las bases son enteros y que si \(\vec{a}_1\), \(\vec{a}_2\) y \(\vec{a}_3\) forman una base, \(\vec{a}_1\times\vec{a}_2\), \(\vec{a}_2\times\vec{a}_3\) y \(\vec{a}_3\times\vec{a}_1\) también lo son. En la Fig. 63 podemos observar como estos últimos vectores son perpendiculares a cada una de las caras formadas por pares de vectores de red.

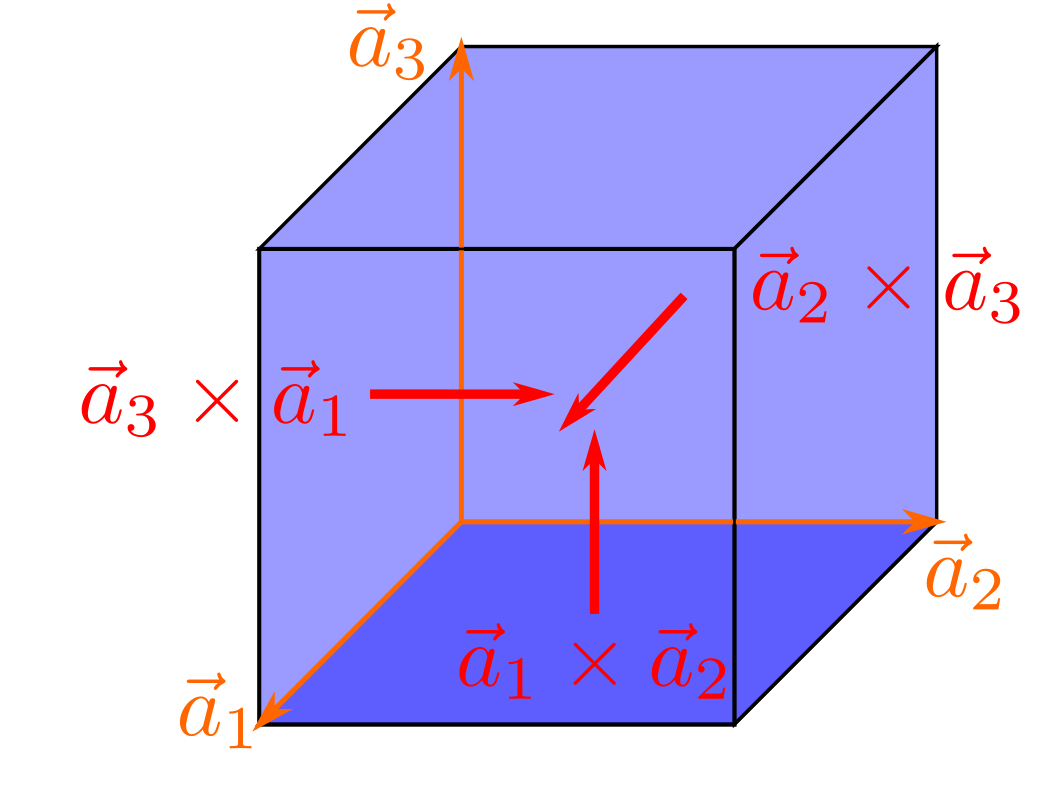
../_images/base_planos.png — Fig. 63 Si \(\vec{a}_1\), \(\vec{a}_2\) y \(\vec{a}_3\) son la base en que expresamos los vectores de red, se puede observar que los productos vectoriales \(\vec{a}_i\times\vec{a}_j\) son perpendiculares a los vectores \(\vec{a}_i\) y \(\vec{a}_j\).#

Precisamente, la red recíproca va a ser la red definida en la Ec. (53) salvo por un factor de normalización. Por tanto, geométricamente esta red va a estar directamente relacionada con los planos de red.

Definición de la red recíproca#

Definición: La red recíproca es la red (primitiva),

(54)#\[\vec{G}=n_1\vec{a}_1^\star+n_2\vec{a}_2^\star+n_3\vec{a}_3^\star,~~~n_i\in\mathbb{Z}\]

donde los vectores de base son,

(55)#\[\vec{a}_1^\star = \frac{2\pi}{V} \vec{a}_2\times\vec{a}_3 \]

(56)#\[\vec{a}_2^\star = \frac{2\pi}{V} \vec{a}_3\times\vec{a}_1\]

(57)#\[\vec{a}_3^\star = \frac{2\pi}{V} \vec{a}_1\times\vec{a}_2\]

y \(V\) es el volumen de la celda primitiva del espacio directo, lo que se puede calcular con un producto mixto de la siguiente manera,

(58)#\[V(\vec{a}_1,\vec{a}_2,\vec{a}_3)=\vert \vec{a}_1\cdot (\vec{a}_2\times\vec{a}_3) \vert.\]

Es importante darse cuenta que para calcular todos los puntos de la red recíproca (o para que la red recíproca tenga algún sentido físico) es importante calcular los puntos de la misma usando la red directa primitiva. Como veremos más abajo también es importante calcular los vectores de la red recíproca convencional, pero tan sólo para dar las coordenadas de los puntos del espacio recíproco en un formato estandarizado.

Relaciones de ortonormalidad#

Es fácil comprobar que los vectores de base de la red recíproca cumplen las siguientes normas de ortonormalidad con los vectores de la red directa,

(59)#\[\vec{a}_i^\star\cdot\vec{a}_j = 2\pi\delta_{ij}\]

donde \(\delta_{ij}\) es la delta de Kronecker. En particular podemos ver que multiplicando dos vectores con el mismo índice obtenemos,

(60)#\[\vec{a}_1^\star \cdot\vec{a}_1 = \frac{2\pi}{V}\left(\vec{a}_2\times\vec{a}_3\right)\cdot\vec{a}_1 = 2\pi,\]

mientras que, si los índices son distintos, tenemos que,

(61)#\[\vec{a}_1^\star \cdot\vec{a}_2 = \frac{2\pi}{V}\left(\vec{a}_2\times\vec{a}_3\right)\cdot\vec{a}_2 = 0\]

En base a estas relaciones podemos probar que el producto escalar de un vector de la red directa con un vector de la red recíproca es un número entero de veces \(2\pi\),

(62)#\[\vec{G}\cdot\vec{R}=\left(n_1\vec{a}_1^\star+n_2\vec{a}_2^\star+n_3\vec{a}_3^\star\right)\cdot\left(m_1\vec{a}_1+m_2\vec{a}_2+m_3\vec{a}_3\right)=2\pi \sum_i n_i m_i = 2\pi N, N\in \mathbb{Z}.\]

Dada la gran utilidad de esta fórmula a la hora de trabajar con ondas en sólidos, en algunos libros[3], se utiliza esta última expresión como la definición de la red recíproca.

Coordenadas#

Cuando se trabaja en sólidos es importante nombrar tanto puntos como familias de puntos en la red directa y en la recíproca. Es por ello que se utilizan diferentes tipos de paréntesis, corchetes y llaves para denotar diferentes objetos. Así, si se desea dar las coordenadas de un punto de la red directa se usan corchetes,

(63)#\[\vec{R}_{111}=[111]=\vec{a}+\vec{b}+\vec{c}\]

donde, como podemos observar, la notación hace referencia a la red convencional, que es la que siempre se usa para dar coordenadas. Por otro lado, si se desea hacer referencia a las coordenadas de la familia de puntos de la red directa equivalentes a uno en particular se utiliza la notación bra-ket[4]. En una red cuadrada, por ejemplo,

(64)#\[\left\langle 11\right\rangle=\{\vec{a}+\vec{b},\vec{a}-\vec{b},-\vec{a}+\vec{b},-\vec{a}-\vec{b}\}.\]

Por otro lado, si se quiere expresar un vector particular de la red recíproca usaremos paréntesis,

(65)#\[\vec{G}_{111}=(111)=\vec{a}^*+\vec{b}^*+\vec{c}^*\]

donde, de nuevo, observamos que el paréntesis denota el uso de la base recíproca convencional. Si, en cambio, usamos llaves la notación se referirá al vector mencionado y todos los equivalentes por simetría. En una red cuadrada, tendríamos,

(66)#\[\left\{ 11\right\}=\{\vec{a}^*+\vec{b}^*,\vec{a}^*-\vec{b}^*,-\vec{a}^*+\vec{b}^*,-\vec{a}^*-\vec{b}^*\}.\]

Ejemplo

En la red representada en la figura inferior tenemos un sólido bidimensional que pertenece al sistema rectangular y su red es rectangular centrada. Los puntos negros representan los puntos de red. Si queremos definir el sistema diremos que es una red rectangular centrada con un átomo en la posición \([0,0]\). También podemos decir que los átomos que están dentro de la primera celda convencional tienen posiciones \([0,0]\) y \([1/2,1/2]\).

En la siguiente sección discutiremos varios ejemplos del cálculo de la red recíproca cuando la periodicidad del sistema es en 1, 2 o 3 dimensiones.