Red recíproca#
La red recíproca y el espacio recíproco son conceptos claves en la física del estado sólido dado, de otro modo, es muy difícil expresar las ondas dentro de los cristales. Son conceptos directamente ligados a las matemáticas de los sistemas periódicos y, al principio, resulta confuso por qué podemos querer utilizar este espacio distinto del espacio real. Es por ello que es muy importante trabajar sobre estos conceptos abstractos y desarrollar una intuición sobre por qué y cómo debemos usarlos.
Alternativas a la descripción de una red periódica#
Imaginemos una red sencilla, con un átomo de motivo y unidimensional, como la que se muestra en la Fig. 60.

Fig. 60 Red unidimensional con n átomos de motivo con posición x=0. El parámetro de malla representa la periodicidad del sistema (T sería el periodo espacial).#
Durante el tema sobre la estructura de moléculas y sólidos discutimos el concepto de Red de Bravais y de parámetro de malla, que en un sólido unidimensional, es equivalente al de periodo. Es decir, que la definición de la red de Bravais,
nos indica que, cada vez que avanzamos una distancia T nos encontramos con un punto de la red. De hecho, no sólo nos encontramos con un punto cuando avanzamos una distancia T si no que también lo hacemos cuando avanzamos 2T, 3T,…, NT.
Es evidente que, si existe un periodo, también debe existir una (o varias) frecuencias,
aunque, dado que el periodo en una red cristalina es una distancia, resulta más adecuado hablar del número de ondas, k.
La red recíproca no va a tratarse de otra cosa que una red de frecuencias,
donde m es un número entero. En algunos casos[3] se suele dar una definición más abstracta, definiendo la red recíproca como los vectores que verifican,
pero es claro que esta última expresión es consecuencia de las Ecs. (44) y (46).
Series de Fourier#
En una estructura periódica, como un cristal, no es sorprendente que, cuando vayamos a describir ondas que se mueven sobre él, como los electrones o las vibraciones cristalinas, las ecuaciones de estas ondas deban (como veremos más adelante mediante el teorema de Bloch) respetar esta simetría (la periodicidad). Es natural, por tanto, que busquemos maneras de describir funciones periódicas como la ilustrada en la Fig. 61. En matemáticas el análisis de estas funciones se conoce como análisis de Fourier y una manera de aproximar las funciones de este tipo es mediante las series de Fourier donde utilizamos funciones oscilantes (senos y cosenos) de cada vez mayor frecuencia (como las de la ecuación Ec. (44)) para incrementar el detalle con el que describimos la función.
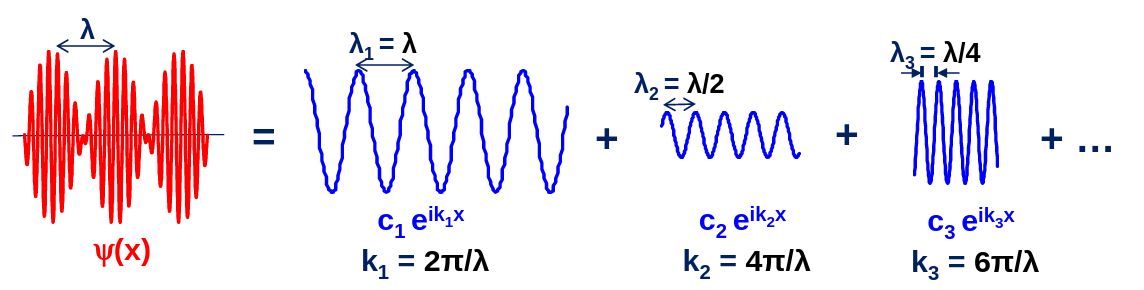
Fig. 61 Esquema de la descomposición de una onda periódica, \(\psi(n)\), a la izquierda y en rojo, en varias de sus componentes de Fourier (en azul). Notar como las frecuencias de la serie coinciden con la red de la Ec. (47).#
Desde un punto de vista físico cada una de las componentes de Fourier representa una onda plana con un momento bien definido,
Podemos comprobar que la función de una onda escrita como una serie de Fourier, es decir, como superposición de ondas planas cuyo vector de ondas viene dado por un vector como el de la Ec. (44),
no varía cuando la trasladamos un vector de la red directa, \(\vec{R}_{lmn}\),
es decir, la función de la onda, \(\psi\) es periódica con la misma periodicidad que la red directa.
Este último resultado apunta a la enorme importancia que tendrá más adelante la red recíproca para escribir las ondas de un sólido.
