Grupos espaciales#
En esta sección vamos a mostrar como los sólidos pueden clasificarse, como las moléculas, de acuerdo con el grupo de las operaciones de simetría que deja el Hamiltoniano electrónico invariante. Vamos a tener dos diferencias importantes, una de fundamento y otra de notación.
En el caso de las moléculas decíamos que se utilizaba el grupo de las operaciones de simetría puntuales, es decir, que fijaban al menos un punto del espacio. En el caso de los sólidos esto no va a ser posible ya que hay un grupo de operaciones de simetría que definen este tipo de material, las traslaciones, que desplazan todo el sistema. Es por ello que en los sólidos usaremos grupos espaciales que contienen traslaciones además de las operaciones puntuales de simetría.
Por otro lado en las moléculas y los grupos puntuales de simetría lo más común es usar la notación de Schönflies (por ejemplo, \(D_{3h}\) o \(O_h\)). En cambio la notación estándar en sólidos es la de Hermann-Mauguin, que describiremos a continuación. Ambos tipos de notación nos van a permitir identificar que simetría tiene el sólido y se trata tan sólo un cambio similar a utilizar un sistema de unidades u otro.
Notación de Hermann-Mauguin#
Los símbolos del grupo de espacio en la notación de Hermann-Mauguin son del tipo
donde \(R\) y los subíndices \(o_a\), \(o_b\) y \(o_c\) (puede haber 1 (\(o_a\)), 2 (\(o_a\),\(o_b\)) o 3 (\(o_a\), \(o_b\), \(o_c\)) son símbolos cuyo significamos damos en las siguientes secciones.
Tres ejemplos de grupos espaciales, junto con el sistema cristalográfico al que pertenecen, son:
Tipo de red (R)#
La letra en mayúscula del símbolo de grupo de Hermann-Mauguin denota el tipo de red de Bravais del cristal, tal y como se indicaba en la Fig. 43. Así puede ser \(P\), \(I\), \(F\) o \(C\).
Subíndices#
Los subíndices (o) que acompañan al tipo de red son símbolos que representan una combinación de operaciones de simetría que es única al grupo de espacio y que, por lo tanto, lo identifican perfectamente. Es importante notar que estas operaciones se han elegido por convenio. Aunque hay otras combinaciones posibles hay unas pocas que se utilizan para facilitar la comunicación de la estructura de los cristales.
De forma similar a las moléculas, en la notación de Hermann-Mauguin es necesario escoger los ejes de coordenadas, dados por los vectores de la red convencional \(\vec{a}\), \(\vec{b}\) y \(\vec{c}\), en direcciones bien definidas por los convenios. Estos convenios vienen resumidos en la tabla de direcciones, Fig. 48, que es clave para poder identificar el grupo de un cristal. La tabla nos indica en que dirección puede presentarse una operación de simetría, ver el ejemplo para más detalles.
Es importante ver que para cada sistema cristalino hay una operación que es clave para identificarlo. Así, todos los grupos hexagonales cuentan con un eje de orden 6 en la primera posición, que representa el eje \(\vec{c}=[0,0,1]\), mientras que los cúbicos tienen un eje de orden 3 en la segunda posición, que representa las direcciones \([1,1,1]\) y equivalentes.
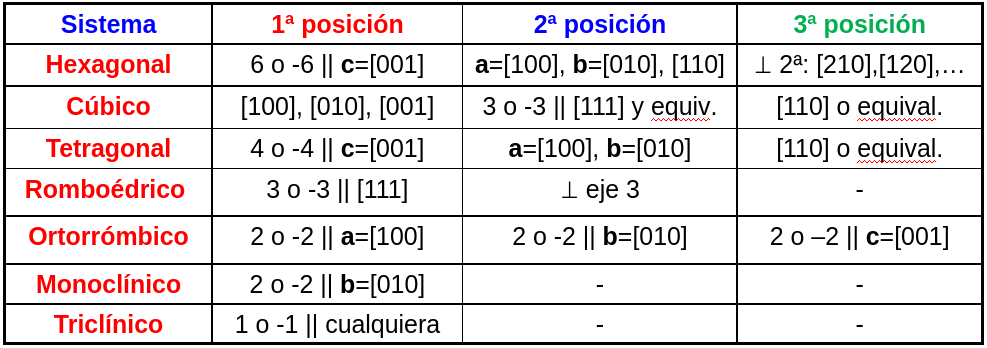
Fig. 48 Tabla que permite identificar la dirección de las operaciones de simetría que identifican un grupo en la notación de Hermann-Mauguin de acuerdo con su sistema cristalográfico. Notar que cada casilla de la tabla contiene tanto la dirección de la operación como si el tipo de operación clave del sistema se encuentra en una dirección particular.#
Ejemplo
Veamos ahora como analizar una estructura cristalina. Para ello tomaremos el ejemplo del cobre metálico, ilustrado en la Fig. 49, que pertenece al grupo \(F_{m-3m}\).
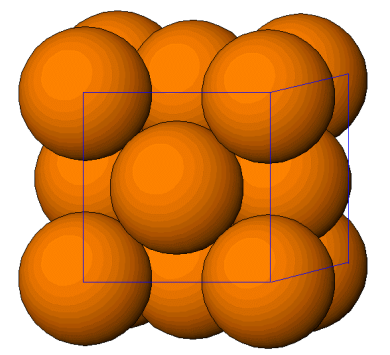
Fig. 49 Ilustración de la estructura tridimensional del cobre metálico donde los átomos se representan por esferas naranjas. Es una estructura denominada cúbica compacta, donde los átomos se colocan de forma que aprovechan óptimamente el espacio. Las líneas representan los bordes de la celda convencional.#
En general nunca vamos a representar las estructuras mediante dibujos en 3 dimensiones como la Fig. 49. Lo que haremos será proyectar las posiciones atómicas de la celda convencional sobre un plano y representar cada uno de los átomos por un círculo. La altura de los diferentes átomos sobre el plano se indicará mediante un número en el interior de círculo. Esta proyección se ilustra en la Fig. 50 donde se muestra la celda convencional proyectada sobre el plano de los ejes \(a\) y \(b\).

Fig. 50 Ilustración de la celda convencional del cobre metálico sobre el plano \(a\)/\(b\). Los números sobre los átomos representan la altura a la que se encuentran del plano \(z=0\), que es perpendicular al eje z.#
En el símbolo del grupo \(F_{m-3m}\) podemos observar:
La letra F representa la red centrada en las caras. Mediante inspección dela Fig. 49 podemos observar que el motivo es un átomo de cobre colocado en la posición [0,0,0].
El primer símbolo del subíndice, \(m\), se corresponde con un plano de reflexión en la dirección \([100]\) (y equivalentes) según la tabla de direcciones, Fig. 48. Este se representa mediante una línea magenta vertical en la Fig. 50 (el plano es perpendicular a \([100]\)).
El segundo símbolo del subíndice, \(-3\), es un eje impropio de rotación en la dirección \([111]\) (y equivalentes) según la tabla de direcciones, Fig. 48. Estos ejes de rotación son característicos de la simetría cúbica y recorren las diagonales principales del cubo que forman los vectores de red (\(\vec{a}\), \(\vec{b}\), \(\vec{c}\)) representado en la Fig. 49.
El tercer y último símbolo del súbindice, \(m\), es un plano de reflexión en la dirección \([110]\) (y equivalentes) según la tabla de direcciones, Fig. 48. Este se representa mediante una línea verde diagonal en la Fig. 50 (el plano es perpendicular a \([110]\) y habría otro equivalente perpendicular a \([-110]\)).
Operaciones de simetría#
Como se ha indicado más arriba las operaciones de simetría de los sólidos pueden ser puntuales, como en las moléculas pero también contienen traslaciones. Además existen operaciones de simetría que combinan ambos tipos de simetría.
Operaciones puntuales de simetría#
Las operaciones puntuales de simetría dejan fijo, al menos, un punto del espacio.
Planos de reflexión e inversión#
Estos elementos son los mismos que en las moléculas. En la notación de Hermann-Mauguin no distinguimos entre planos verticales u horizontales y a todos los denotamos con la letra \(m\).
Cuando vemos un plano \(m\) en un símbolo de grupo de espacio viene definido por una dirección que es perpendicular al plano de reflexión (recordemos que un plano siempre se caracteriza por un vector director que es el que tendremos que buscar en la tabla de direcciones, Fig. 48).
En Hermann-Mauguin una inversión se identifica por el número \(-1\) por motivos que veremos a continuación.
Rotaciones#
Como en el caso de la notación de Schönflies los cristales pueden quedar invariantes cuando los rotamos, de forma propia o impropia, alrededor de un eje hasta n veces. El orden de la rotación, n, hace que el sólido permanezca invariante cuando el ángulo de rotación es \(2\pi/n\).
Rotaciones propias#
Las rotaciones propias son equivalentes a las rotaciones propias en moléculas. Se rota al sólido un ángulo medido en sentido contrario a la agujas del reloj a lo largo de un eje que viene dado por una de las direcciones principales del sólido, Fig. 48. Por ejemplo, en la Fig. 51 se muestra un eje de orden 3.

Fig. 51 Esquema sencillo que muestra una figura con un eje de orden 3.#
La notación de las rotaciones propias en sólidos es un número que representa el orden de la rotación. Es decir, que una rotación \(C_4\) en Schönflies se denota \(4\) en Hermann-Mauguin.
Rotaciones impropias#
Las rotaciones impropias en sólidos son similares a las de las moléculas con la diferencia de que, en vez de combinar una rotación y una reflexión, combinan una rotación y una inversión. En Hermann-Mauguin se denotan mediante un número negativo que indica el orden de la rotación impropia. En la Fig. 52 se muestra una rotación impropia de segundo orden (\(-2\)), a lo largo de la línea roja en el dibujo central.

Fig. 52 Esquema sencillo que muestra el efecto de una rotación impropia de orden 2, consistente en una rotación de orden 2 a lo largo de la línea roja seguida de una inversión.#
Es sencillo ver que, como en las moléculas, la inversión y el plano de reflexión son casos particulares de las rotaciones impropias. En particular la inversión es la operación \(-1\) mientras que el plano de reflexión es \(-2\), como puede observarse en la Fig. 52.
Límites a las rotaciones#
A diferencia de las moléculas, en los sólidos no podemos tener cualquier tipo de eje de rotación si no que tan sólo pueden existir ciertos tipos (1, 2, 3 ,4, 6). Veamos como surge esta propiedad considerando la Fig. 53.

Fig. 53 Esquema de la demostración de que sólo algunos tipos de rotaciones son posibles en sólidos.#
Supongamos que \(A\) y \(B\) son puntos de una red de Bravais y que están separados por una distancia a,
Ahora aplicamos una rotación de un ángulo \(\alpha\) alrededor de \(A\). Eso significa que \(B\) pasaría a una posición \(B^\prime\). Del mismo modo, si tenemos la operación sobre \(A\) y, dado que todos los puntos de una red de Bravais son equivalentes, podemos aplicar sobre \(B\) la operación inversa a la rotación \(\alpha\) (una rotación \(-\alpha\)) lo que transporta \(A\) sobre \(A^\prime\).
Si la operación de rotación es de simetría tiene que transportar, necesariamente, un punto de red sobre otro punto de red. Por tanto, el segmento \(\bar{A^\prime B^\prime}\), que es paralelo a \(\bar{AB}\), tiene que estar separado por un número entero de veces la distancia a,
Imponiendo esta condición y con ayuda de un poco de trigonometría (ver Fig. 53) vemos que los valores de \(\alpha\) están limitados según indica la Tabla de ángulos, Fig. 54.

Fig. 54 Ángulos de rotación permitidos en un sólido.#
Combinaciones de operaciones puntuales#
En algunos casos en los símbolos de grupo se pueden observar subíndices que denotan, al mismo tiempo, la presencia de una rotación y un plano de reflexión perpendicular a la misma en cierta dirección. Estos símbolos son “n/m” donde n es el orden de la rotación (\(2/m\), \(3/m\), \(4/m\), \(6/m\)) y \(m\) representa el plano de reflexión.
Grupos puntuales#
A diferencia de las moléculas donde puede haber infinitos grupos puntuales debido a la falta de restricciones sobre el orden de las rotaciones en el caso de un sólido el número de grupos puntuales es, tan sólo, 32 (en el caso de periodicidad en 3 dimensiones). En la Tabla grupos puntuales, Fig. 55, pueden encontrarse los 32 grupos en notación de Hermann-Mauguin (y Schönflies entre paréntesis) catalogados de acuerdo con su sistema cristalino.
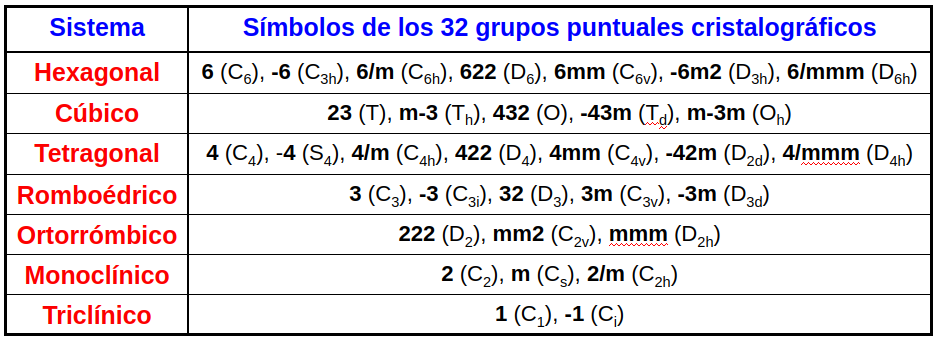
Fig. 55 Grupos puntuales de los sólidos clasificadso según su sistema cristalino junto tanto en notación de Hermann-Mauguin como de Schönflies.#
Traslaciones#
Por su definición, está claro que todas las traslaciones de los vectores de red de una celda convencional son operaciones de simetría. A estas traslaciones las denominamos traslaciones enteras. En aquellos casos en los que la celda primitiva no sea igual a la convencional las traslaciones de los vectores de red primitivos también serán operaciones de simetría diferentes a las traslaciones enteras que implican traslaciones de fracciones de vectores de red convencionales.
Realmente, todas estas operaciones de simetría se encuentran ya recogidas en el símbolo de la red de Bravais del grupo de espacio.
Operaciones mixtas puntual/traslación#
Hay un tercer tipo de operación de simetría en los grupos espaciales que combina una operación de simetría puntual y una traslación fraccionaria. Estos son los ejes helicoidales y los planos/líneas de deslizamiento que introducimos a continuación.
Ejes helicoidales#
Un eje helicoidal combina un eje propio de rotación de orden n con una traslación fraccionaria a lo largo del eje. Estas operaciones se denotan con un símbolo \(n_m\) que significa que se debe hacer una rotación de orden n seguida de una traslación \(m/n\) a lo largo de la dirección del eje de rotación. Varios de estos ejes helicoidales vienen ilustrados en la Fig. 56.
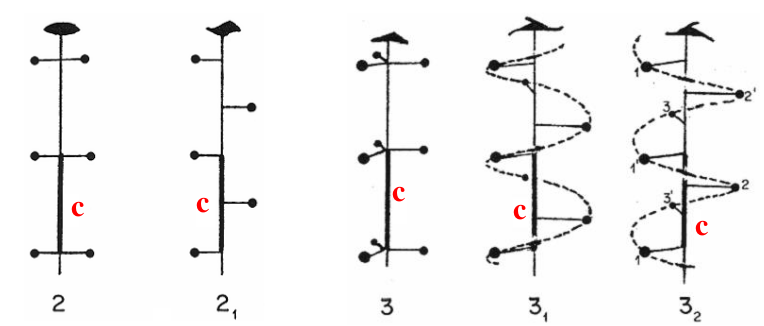
Fig. 56 Ilustración de varios ejes helicoidales, todos a lo largo de la dirección \(\vec{c}\) de un cristal. La figura muestra, para cada caso, la rotación pura (\(2\), \(3\)) y los ejes helicoidales asociados a ese tipo de eje con traslaciones para las diferentes posibles fracciones del orden de rotación.#
En la Fig. 57 se muestra la notación de la Unión Internacional de Cristalografía para todos los tipos de eje helicoidales posibles.

Fig. 57 Notación de la Unión Internacional de Cristalografía para todos los tipos de ejes helicoidales posibles en cristales.#
Planos de deslizamiento#
Los planos (y líneas para sólidos periódicos en 2 dimensiones) de deslizamiento consisten en un plano de reflexión combinado con una traslación paralela al plano.
Ejemplo
Esto viene ilustrado en la Fig. 58. Esta estructura bidimensional tiene una celda rectangular de vectores convencionales \(\vec{a}\) y \(\vec{b}\).
Ahí puede observarse que, aunque cada fila vertical de perros es claramente equivalente a las otras, un plano de reflexión sencillo no permite transformar una fila en otra.
Podemos verlo haciendo una reflexión a lo largo de la línea de deslizamiento g, donde encontramos que los perros a la izquierda de la línea, que miran hacia la derecha, pasan a la derecha de la misma mirando a la izquierda. Pero la imagen especular no está alineada verticalmente respecto a los perros originales.
Para alinearlos tenemos que desplazar la imagen especular medio vector \(\vec{b}\) que es lo que completa la línea de deslizamiento de tipo g.
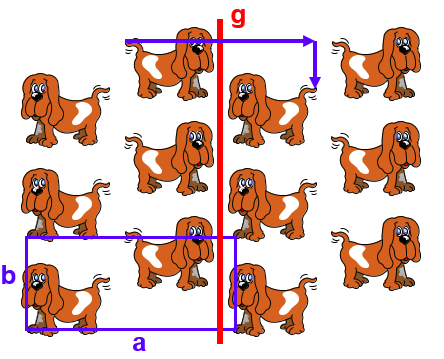
Fig. 58 Planos deslizamiento perros#
La notación de los planos de deslizamiento viene resumida en la Tabla Fig. 59 donde se observa que se denotan por las letras \(a\), \(b\) \(c\), \(n\) y \(d\). El plano de un plano de deslizamiento siempre será perpendicular a la dirección característica del índice donde aparezca (ver Tabla de direcciones, Fig. 48) y el símbolo que lo represente vendrá dado por el tipo de desplazamiento que tenga asociado.
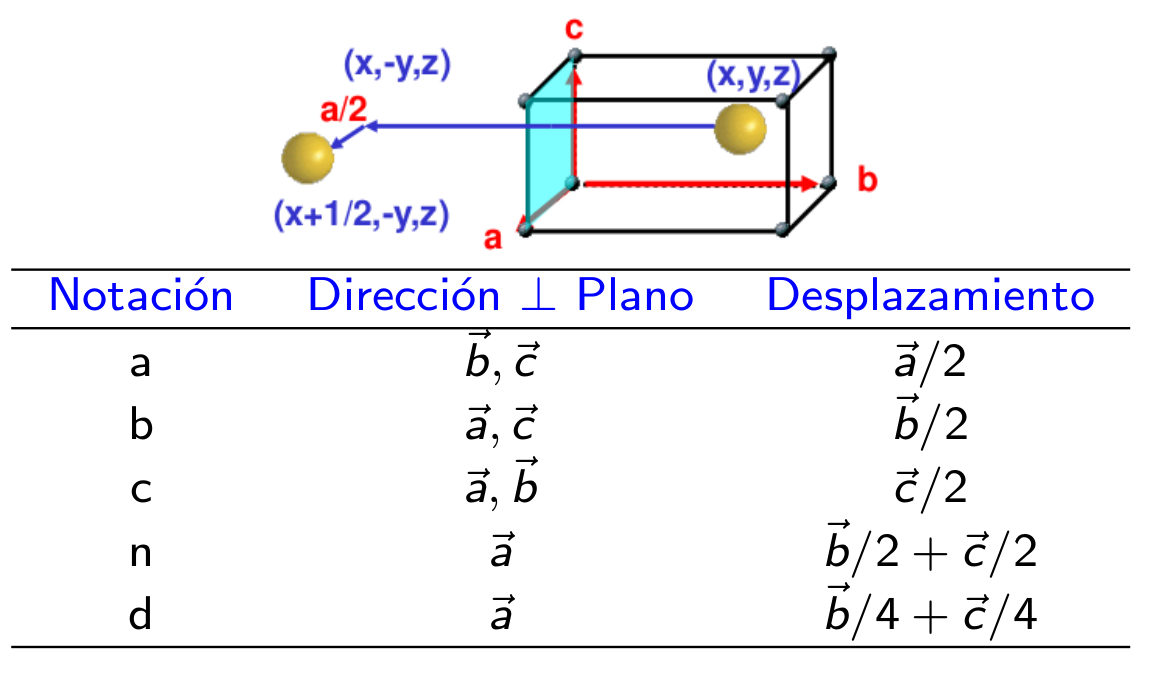
Fig. 59 Tabla enumerando los diferentes tipos de plano de deslizamiento. La dirección del plano viene dada por su posición dentro del símbolo, de acuerdo con la Tabla de direcciones, Fig. 48, (por ejemplo un plano en la tercera posición de un sistema cúbico sería perpendicular a \([110]\) y planos equivalentes). La dirección del desplazamiento viene dada por la notación indicada en esta tabla. Por ejemplo, los planos de tipo a siempre desplazan el sistema medio vector de red a lo largo de \(\vec{a}\).#
Así (ver Tabla de los planos de deslizamiento, Fig. 59) \(a\), \(b\) o \(c\) siempre son desplazamientos de medio vector de red en la dirección indicada por la letra, es decir desplazamientos \(\vec{a}/2\), \(\vec{b}/2\) o \(\vec{c}/2\), respectivamente.
En cambio un desplazamiento \(n\) representa un desplazamiento de medio vector de red en las dos direcciones perpendiculares al plano. Así un plano \(n\) que sea perpendicular a \(\vec{a}\) (por ejemplo que esté en la primera posición de un sistema ortorrómbico, Fig. 48) tendrá asociado una traslación de medio vector a lo largo de \(b\) y \(c\), es decir, \(\vec{b}/2+\vec{c}/2\).
Finalmente un desplazamiento tipo \(d\) es equivalente a un \(n\) salvo que los desplazamientos son de 1/4 de vector de red en vez de 1/2.
Tablas e información en la web#
En cristalografía es muy importante usar las tablas y los diagramas que nos provee la Unión Internacional de Cristalografía Tablas internacionales de cristalografía. De forma gratuita se pueden encontrar en el Bilbao Crystallographic Server, una serie de utilidades en la web que nos pueden permitir utilizar toda la potencia de la cristalografía.
