Representaciones irreducibles

En la sección anterior se ha tratado como expresar los operadores en una base, formada por algunos orbitales atómicos importantes para el problema, y como esto lleva, de forma natural, a expresarlos como una matriz. En esta sección se va a discutir como utilizar el álgebra de matrices, en particular el cambio de base o representación, para encontrar métodos que nos ayuden a resolver el problema electrónico asociado a las ecuaciones de Hartree-Fock.

Representaciones reducibles

Si nuestra base de orbitales atómicos, la representación de nuestros operadores, está formada por los orbitales \(\{\chi\}\) en álgebra se llama cambio de base a una transformación lineal del tipo,

(210)\[\left\vert \chi_a^\prime \right\rangle = \sum_b U_{ab} \left\vert \chi_b \right\rangle \]

donde las funciones \(\{\chi^\prime\}\) definen una base diferente a \(\{\chi\}\) y la matriz \(U_{ab}\) relaciona la primera y la segunda base.

Para que \(\{\chi^\prime\}\) sea realmente una base sus vectores tienen que expandir un espacio de dimensión N, donde N es el número de funciones en la base. Si \(\{\chi\}\) lo cumple, la condición para que \(\{\chi^\prime\}\) sea una base es que el determinante de la transformación, \(detU\), sea no nulo.

Definición: Se dice que la representación \(\Gamma =\{D(R), R\in G\}\) del grupo \(G\) es reducible si, con un cambio de base, la representación matricial pasa a ser diagonal por cajas. Es decir, en la nueva base todas las operaciones de simetría tienen la misma estructura por cajas (ver ejemplo más abajo).

Físicamente esto va a significar que hay funciones de la base que están relacionadas por simetría, y que caerán en la misma caja, que son diferentes de otras, que estarán en cajas diferentes.

Ejemplo: funciones N(2p) en el Amoníaco

Estudiemos la representación de las operaciones de simetría del amoníaco en la base de las tres funciones 2p del átomo de nitrógeno, que se encuentra en el centro de la molécula. Esta representación, ya discutida en la sección sobre elementos de matriz, se discute en las figuras siguientes.

Fig. 133 En la representación de los orbitales 2p del nitrógeno la operación \(C_3^-\) aparece por cajas. Una asociada a los orbitales 2\(p_x\) y 2\(p_y\) (en amarillo) y otro al orbital 2\(p_z\) (en verde).

Fig. 134 En la representación de los orbitales 2p del nitrógeno la operación \(C_3^+\) aparece por cajas. Una asociada a los orbitales 2\(p_x\) y 2\(p_y\) (en amarillo) y otro al orbital 2\(p_z\) (en verde).

Fig. 135 En la representación de los orbitales 2p del nitrógeno la identidad aparece por cajas. Aunque la hacemos más grande para que sea igual que en otras operaciones, una asociada a los orbitales 2\(p_x\) y 2\(p_y\) (en amarillo) y otra al orbital 2\(p_z\) (en verde).

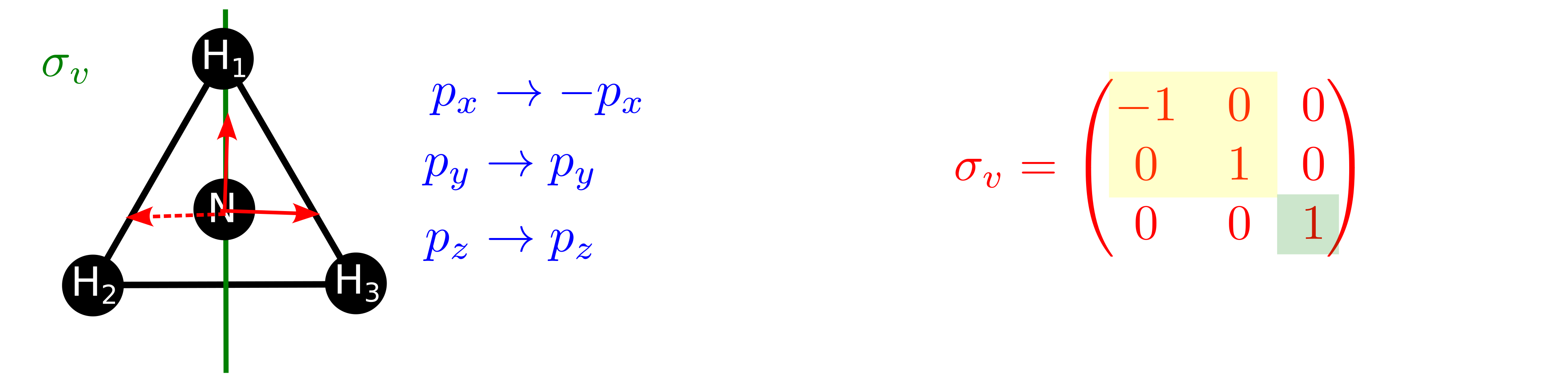
Fig. 136 En la representación de los orbitales 2p del nitrógeno la operación \(\sigma_v\) aparece por cajas. Aunque la hacemos más grande para que sea igual que en otras operaciones, una asociada a los orbitales 2\(p_x\) y 2\(p_y\) (en amarillo) y otra al orbital 2\(p_z\) (en verde).

Fig. 137 En la representación de los orbitales 2p del nitrógeno la operación \(\sigma_v^\prime\) aparece por cajas. Una asociada a los orbitales 2\(p_x\) y 2\(p_y\) (en amarillo) y otro al orbital 2\(p_z\) (en verde).

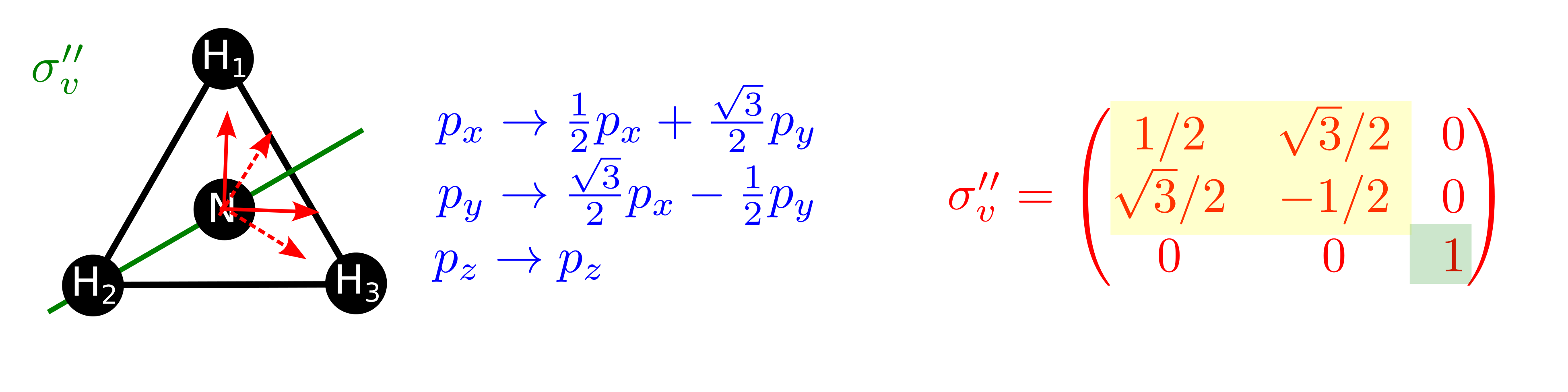
Fig. 138 En la representación de los orbitales 2p del nitrógeno la operación \(\sigma_v^{\prime\prime}\) aparece por cajas. Una asociada a los orbitales 2\(p_x\) y 2\(p_y\) (en amarillo) y otro al orbital 2\(p_z\) (en verde).

Podemos ver que en la representación \(2p_x\), \(2p_y\), \(2p_z\) las matrices que simbolizan las operaciones de simetría ya aparecen por cajas, indicado por un sombreado amarillo y otro verde en las figuras anteriores. En particular, podemos ver que hay una caja que se corresponde con los orbitales \(2p_x\) y \(2p_y\) y una caja diferente para el orbital \(2p_z\).

Dado que una representación reducible puede separarse en cajas independientes, cada una con su propia representación podemos decir que la representación inicial puede expresarse como suma directa de las representaciones más pequeñas,

(211)\[D(R)=a_1 D_1(R)\oplus a_2 D_2(R) \oplus \cdots\]

donde los coeficientes \(a_i\) indican el número de veces que aparece esa representación en la reducción.

La pregunta más directa que podemos hacernos es, ¿hay un límite a la reducción de representaciones? que responderemos en la próxima sección.

Representaciones irreducibles

Definición: Una representación irreducible es aquella que no puede reducirse más. En general llamamos irrep a las representaciones irreducibles.

Se pueden probar las siguientes propiedades de las irreps:

• Las representaciones de dimensión \(d=1\) son irreducibles. Esta propiedad es trivial ya que no es posible reducir por cajas una matriz 1x1. No todas las irreps tienen dimensión 1, en física y química molecular las hay, también, con dimensión 2, 3, 4 o 5.

• Los tipos de irreps de cada grupo son conocidos y están tabuladas en las tablas de caracteres. En física y química se utilizan las tablas para los grupos puntuales. Las tablas más usadas en formato imprimible son las de Atkins.

• Cualquier matrices pueden reducirse a una suma directa de matrices de las diferentes irreps. En la Fig. 139 se muestra una matriz por cajas donde hay 2 irreps, una representada por el área rojo y otra por el área amarilla.

Fig. 139 Matriz expresada en una base simetrizada donde cada función pertenece a una irrep. La matriz se divide en cajas aislada, cada una asociada a una irrep.

Definición: Decimos que una función \(\psi_i^\ell\) pertenece a la irrep \(\Gamma_\ell\) si cumple que, para toda operación de simetría R del grupo,

(212)\[R\psi_i^\ell \in \Gamma_\ell\]

Teniendo en cuenta la forma que tienen las matrices de las operaciones de simetría por irreps (Fig. 139) es fácil darse cuenta que la función de la irrep está expandida por las funciones de base que representan esa irrep en particular:

(213)\[\psi_i^\ell=\sum_a c_{ia} \left\vert \chi_a \right\rangle~ /~\chi_a \in \Gamma_\ell\]

es decir, que al multiplicar por las matrices de la Fig. 139 el resultado va a permanecer dentro de las funciones que generan la caja (una combinación lineal de estas funciones).

Esta expresión es una generalización de la definición del carácter de una función (Ec. (209)). Si la irrep tiene dimensión 1 tenemos que la Ec. (212) se convierte en,

(214)\[R\psi_i^\ell=r_\ell \psi_i^\ell\]

es decir, en las irreps de dimensión 1 las funciones de onda coinciden con autovectores de las operaciones de simetría.

Tabla de caracteres

Como se ha indicado anteriormente, las irreps de cada grupo puntual se encuentran clasificadas en tablas. En la Fig. tabla se presenta la tabla correspondiente al grupo \(D_{\infty h}\) para las moléculas lineales con centro de inversión.

Fig. 140 Tabla de caracteres del grupo \(D_{\infty h}\) (Atkins).

En esta tabla es importante apreciar como:

• La fila superior representa las clases de las operaciones de simetría del sistema.

• El resto de las filas comienzan con una etiqueta que se asocia con la irrep.

• Para cada irrep y por columnas podemos ver el carácter, es decir, la traza de su submatriz, asociado a cada clase de operaciones.

• Cada irrep se caracteriza por un conjunto único de caracteres.

Es decir, las irreps representan un código único (una etiqueta), que identifica como se transforman ciertas combinaciones lineales de orbitales atómicos. Si a esto unimos la Ec. (214) que asociamos a los números cuánticos tenemos que la irrep representa el conjunto de números cuánticos que determinan el estado de un sistema (ver la sección Funciones atómicas más abajo donde se discute un ejemplo de gran importancia).

Notación de Mulliken

La notación usada para describir las irreps en moléculas se debe a Robert S. Mulliken, una figura clave en el desarrollo de la física química.

En la notación de Mulliken las irreps contienen un símbolo principal, que puede ser:

• A o B tienen dimensión 1. Las irreps A son simétricas respecto al eje principal (su aplicación da la misma función de onda) y las B son antisimétricas (cuando aplicamos la rotación del eje principal la función de onda cambia de signo).

• E tienen dimensión 2. Se requiere, al menos, un eje de orden 3.

• T tienen dimensión 3. Sólo aparecen en los grupos cúbicos \(O\), \(O_h\) y en los icosaédricos \(I\), \(I_h\).

• G, H tienen dimensión 4 y 5, respectivamente. Sólo aparecen en los grupos icosaédricos \(I\) e \(I_h\).

Y, además, pueden tener subíndices:

• Subíndice 1 o 2 indica que son simétricas/antisimétricas respecto a una rotación \(C_2\) perpendicular al eje principal (si no hay \(C_2\), respecto a \(\sigma_v\)).

• Subíndice g o u indica que son simétricas/antisimétricas respecto a la inversión (i), si la hubiera.

y superíndices,

• Superíndice \(\prime\), \(\prime\prime\) indican funciones simétricas/antisimétricas respecto a \(\sigma_h\), si lo hubiera.

En grupos lineales, por motivos históricos la notación es algo diferente.

• \(\Sigma\)(s) es una irrep de dimensión 1, que representa una función de momento angular \(m_l=0\) y tiene simetría cilíndrica alrededor del eje z.

• \(\Pi\)(p) es una irrep de dimensión 2, que representan funciones de momento angular \(m_l=\pm 1\)

• \(\Delta\)(d) es una irrep de dimensión 2, que representan funciones de momento angular \(m_l=\pm 2\)

• Subíndices +/- indican que son simétricas/antisimétricas respecto a los planos \(\sigma_v\).

Ejemplo: Tabla de caracteres del amoníaco

En la figura siguiente se presenta la tabla de caracteres del grupo \(C_{3v}\) al que pertenece la molécula de amoníaco con etiquetas explicativas.

Fig. 141 Tabla de caracteres del grupo \(C_{3v}\) al que pertenece el amoníaco. Se indican las diferentes partes de la Tabla con colores. En azul se muestran las clases de operaciones de simetría, en rojo las diferentes irreps y los caracteres, en magenta como se transforman las funciones lineales (x, y, z) y cuadráticas (\(x^2+y^2\),…) según su irrep.

Podemos ver (primera fila) que hay 3 clases de operaciones, la identidad (\(E\)) la clase de las rotaciones de orden 3 que contiene dos operaciones (\(C_3^+\) y \(C_3^-\)). También vemos que (primera columna) hay 3 irreps, \(A_1\), \(A_2\) y \(E\) que, de acuerdo a la notación de Mulliken tienen, respectivamente, dimensión 1, 1 y 2. Esta dimensión coincide con el carácter de la identidad.

Los números en la tabla son los caracteres que, como decíamos, son los número cuánticos que identifican a los estados. Por ejemplo, un orbital s del nitrógeno,

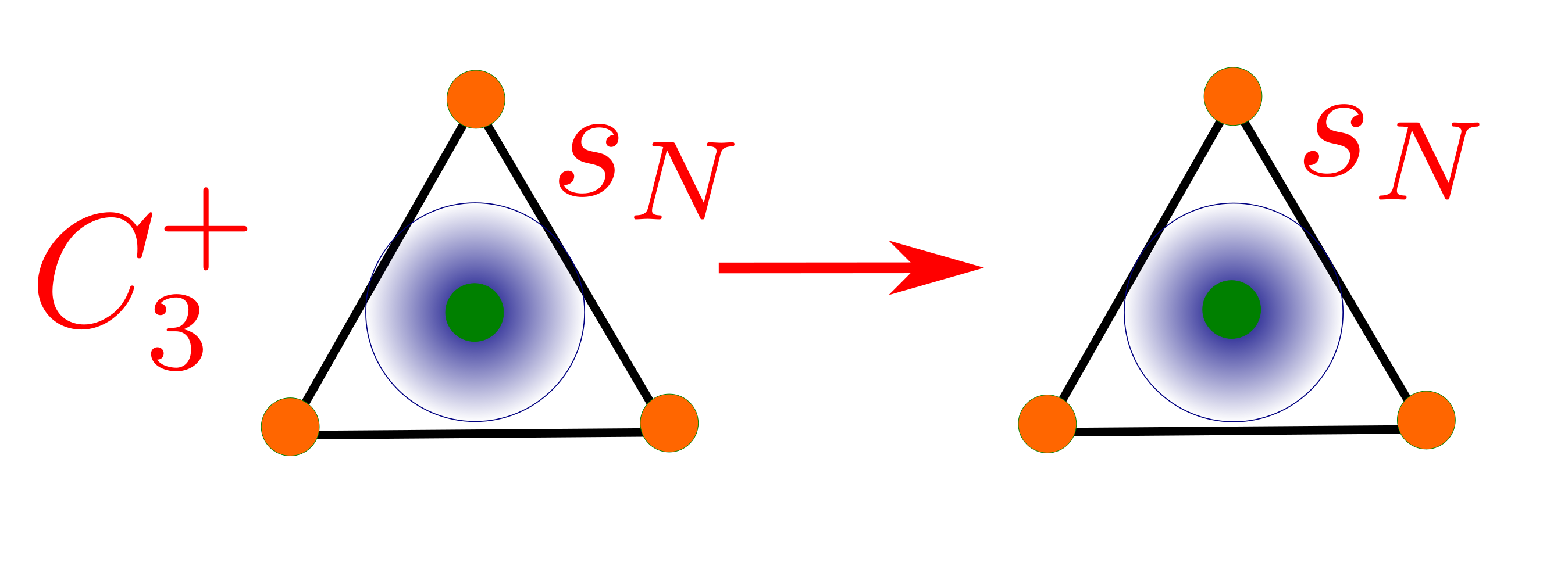
Fig. 142 Transformación del orbital 2s de nitrógeno bajo la operación \(C_3⁺\). El orbital queda invariante por lo que su carácter es 1.

es invariante bajo cualquier operación de simetría (al aplicar la operación de simetría siempre obtenemos el orbital inicial) por ejemplo,

\(C_3^+ \left\vert N(2s) \right\rangle = 1 \cdot \left\vert N(2s) \right\rangle \) por lo que, comparando con la Ec. (214) vemos que todos los caracteres son 1. Es por ello que la irrep de un orbital N(2s) en el amoníaco es \(A_1\) (ver Fig. 141 ).

Por otro lado, cuando aplicamos operaciones de simetría sobre \(p_x\) y \(p_y\) tenemos que se interconvierten unas en otras (ver Fig. 143). Estas dos funciones están relacionadas por simetría y, cuando vemos la traza de su caja (el carácter) para cada operación de simetría vemos que el resultado coincide con la etiqueta \(E\). Es decir, \(p_x\) y \(p_y\) generan una irrep de dimensión 2.

Fig. 143 Tranformación de los orbitales 2\(p_x\) y 2\(p_y\) del nitrógeno en el amoníaco bajo rotaciones del eje \(C_3\).

Finalmente, en la parte derecha de la tabla aparece que funciones sencillas se transforman de acuerdo como una irrep. Esto es importante ya que las funciones p se transforman como x, y o z y las funciones d como productos cuadráticos tipo \(xy\), \(xz\), etc. Los símbolos \(R_x\), \(R_y\) o \(R_z\) son rotaciones rígidas que serán útiles más adelante.

Funciones atómicas y moleculares

La notación de Mulliken puede resultar nueva a este curso pero el concepto de irrep como etiqueta que define números cuánticos debe resultar ya conocido. Cuando en física atómica hablamos de funciones s, p, d,… sabemos que nos referimos a orbitales con cierto momento angular (\(\ell=0, 1, 2,...\)). Además sabemos que hay una función s, 3 funciones p, 5 funciones d, etc. Desde el punto de vista de las irreps \(s\) es un orbital que se transforma siempre en sí mismo (\(a_1\)), \(p\) cambia de signo cuando lo rotamos 180\(^o\) a lo largo de dos ejes pero no el tercero o cuando aplicamos la inversión, etc. Es decir, que las etiquetas \(s\), \(p\) o \(d\) se refieren a irreps de dimensión 1, 3 y 5 respectivamente.

En las moléculas lineales, cuya tabla de caracteres está en la Fig. 140 podemos ver que las irreps son \(\Sigma\), \(\Pi\), \(\Delta\) que son las letras griegas para s, p y d y que, además, representan funciones de momento angular orbital \(m_l=0\), \(m_l=1\) y \(m_l=2\), respectivamente. Esto es debido a que en estos sistemas hay, al menos, un eje de rotación que no cambia el sistema independientemente del ángulo rotado lo que lleva a la conservación del momento angular.

Reducción de representaciones

Finalmente llegamos a la parte más práctica para el uso de la teoría de grupos en física. Si podemos encontrar una manera sistemática de reducir la representación del sistema eso puede implicar que, cuando diagonalicemos el Hamiltoniano, podamos separarlo en pequeñas cajas que sean más sencillas de diagonalizar. A esta técnica se le denomina la reducción de representaciones.

Para ello, como indicábamos al principio de la sección, lo que se va a hacer es un cambio de representación (base) \(\{\chi\}\rightarrow\{\chi^\prime\}\) que diagonalice por cajas las operaciones de simetría Ec. (210).

Al hacer un cambio de base, Ec. (210), las operaciones se van a transformar del siguiente modo,

(215)\[R^\prime=U^{-1}RU.\]

Lo primero que se probará es que el carácter de una matriz no cambia con su representación. En particular,

(216)\[\chi(R^\prime)=\sum_i R^\prime_{ii} = \sum_i \sum_{jk} U^{-1}_{ij} R_{jk} U_{ki} = \sum_{jk} R_{jk} \left(\sum_i U_{ki} U^{-1}_{ij}\right) = \sum_{jk} R_{jk} \delta_{jk} = \sum_j R_{jj}=\chi(R)\]

Por lo tanto, podemos afirmar que el carácter de una operación, dado que es reducible es la suma de los caracteres de cada una de las irreps que lo forma,

(217)\[D(R)=a_1 D_1(R)\oplus a_2 D_2(R) \oplus \cdots \rightarrow \chi(R)=\sum_{\ell} a_\ell \chi_\ell\]

Ahora podemos encontrar los coeficientes \(a_\ell\) aplicando el gran teorema de ortogonalización tal y como se discute en el capítulo 7 de la Ref.[11].

(218)\[a_{\ell} = \frac{1}{h}\sum_R \chi^{\ell}(R)^\star \chi(R) = \frac{1}{h} \sum_c g(c) \chi^{\ell}(c)^\star \chi(c)\]

En esta fórmula h es el número total de operaciones (la suma de la primera fila de la tabla de caracteres), \(d_\ell\) es la dimensión de la irrep \(\ell\) y g(c) es el número de operaciones en la clase c (el número que aparece en la primera fila de la tabla de caracteres, ver Fig. 141).

(219)\[\psi=\sum_{i\ell} \psi_i^{\ell} ~ \mid ~ R\psi_i^{\ell}\in \Gamma_\ell\]

Cualquier función dentro del espacio de la base \(\{\chi\}\) la podemos escribir como la suma de componentes por irreps. Es decir, cualquier función de onda \(\psi\) cumple que,

(220)\[p^{\ell}\psi=\sum_{i}\psi^\ell_i\]

Para encontrar cada una de las partes de la función que se transforma como una irrep particular, \(\psi_i^\ell\), podemos utilizar los proyectores,

(221)\[p^{\ell}=\frac{d_\ell}{h}\sum_R\chi^\ell(R)^\star R \]

donde \(d_\ell\) es la dimensión de la irrep \(\ell\).

Cuando aplicamos un proyector sobre una función \(\psi\), \(p^{\ell}\psi\),

• Nos da la parte de la función de onda correspondiente a la irrep \(\Gamma_\ell\)

(222)\[p^{\ell}\psi=\sum_{i}\psi^\ell_i\]

• El resultado no está normalizado, de hecho puede ser cero si la función \(\psi\) no contiene ninguna parte que se transforme como \(\Gamma_\ell\).

• Dada una base, aplicando el proyector a cada uno de los elementos de la misma podemos encontrar una nueva base pero simetrizada, es decir, donde cada uno de los elementos se transforma de acuerdo a una irrep.

Ejemplo

Apliquemos ahora el procedimiento de reducción al ejemplo de los orbitales H(1s) y N(2s) dentro de la molécula de amoníaco. El objetivo es, partiendo de la base \(\{N(2s),H_1(1s),H_2(1s),H_3(1s)\}\), hacer una transformación de base cuyos vectores se transformen de acuerdo a una irrep determinada. Los orbitales y la tabla de caracteres del grupo \(C_{3v}\) se encuentran en la Fig. 144.

Fig. 144 Ilustración de los orbitals 1s del hidrógeno (\(s_1\), \(s_2\), \(s_3\)) y el 2s del nitrógeno (\(s_4\)) en el amoníaco. Se muestra también la tabla de caracteres del grupo \(C_{3v}\) al que pertenece el amoníaco.

El primer paso consiste en encontrar la representación de las operaciones del grupo en esta base y calcular el carácter de cada una mediante la traza de la matriz. Siguiendo el procedimiento descrito anteriormente obtenemos, para cada operación:

(223)\[\begin{split}I= \begin{pmatrix} 1 & 0 & 0 & 0\\ 0& 1& 0 & 0\\0&0&1&0\\0&0&0&1\end{pmatrix} \rightarrow \chi(I)=4\end{split}\]

(224)\[\begin{split}C_3^+= \begin{pmatrix} 0 & 0 & 1 & 0 \\ 1& 0& 0 &0\\0&1&0 & 0\\0&0&0&1\end{pmatrix} \rightarrow \chi(I)=1 \end{split}\]

(225)\[\begin{split}C_3^-= \begin{pmatrix} 0 & 1 & 0 & 0\\ 0& 0& 1 &0 \\1&0&0 & 0\\0&0&0&1\end{pmatrix} \rightarrow \chi(I)=1 \end{split}\]

(226)\[\begin{split}\sigma_v= \begin{pmatrix} 1 & 0 & 0 &0 \\ 0& 0& 1 &0 \\0&1&0 & 0\\0&0&0&1\end{pmatrix} \rightarrow \chi(I)=2 \end{split}\]

(227)\[\begin{split}\sigma_v^\prime= \begin{pmatrix} 0 & 1 & 0 &0 \\ 1& 0& 0 &0 \\0&0&1 & 0\\0&0&0&1\end{pmatrix} \rightarrow \chi(I)=2 \end{split}\]

(228)\[\begin{split}\sigma_v^{\prime\prime}= \begin{pmatrix} 0 & 0 & 1 &0 \\ 0& 1& 0 &0 \\1&0&0 & 0\\0&0&0&1\end{pmatrix} \rightarrow \chi(I)=2 \end{split}\]

Podemos observar como el carácter de las operaciones de la misma clase (rotaciones entre sí y planos de reflexión entre sí) es siempre el mismo.

Utilizaremos ahora la Ec. (218) para saber cuantas funciones de onda de cada irrep expande nuestra base (\(a_{\ell}\)). En esta fórmula h es el número de operaciones del grupo que, como hemos mostrado arriba, son 6. Además tenemos que sumar sobre las clases (c) que son, respectivamente, la de la identidad, la de las rotaciones y la de los planos.

Veamos cuantas funciones de tipo \(A_1\) expande nuestra base. Teniendo en cuenta que el número de operaciones por clase (\(g(c)\)) son 1 (identidad), 2 (rotaciones) y 3 (planos), que el carácter de las clases de operaciones (\(\chi^\ell(c)\)) para la irrep \(A_1\) (las entradas de la tabla de caracteres para \(A_1\)) son 1 (identidad), 1 (rotaciones) y 1 (planos) y que el carácter de las operaciones (\(\chi(c)\)) son 4 (identidad), 1 (rotaciones) y 2 (planos) se obtiene:

(229)\[ A_1 \rightarrow a_{A_1}=\frac{1}{6} \left(1 \times 1 \times 4 + 2 \times 1 \times 1 + 3 \times 1 \times 2\right) = 2\]

Es decir, de la base \(\{N(2s),H_1(1s),H_2(1s),H_3(1s)\}\) podemos extraer 2 funciones que pertenece a la irrep \(A_1\).

Si aplicamos los mismos principios a las irreps \(A_2\) y \(E\), aplicando la misma fórmula pero cambiando tan sólo los caracteres de cada clase para la irrep (las entradas en la tabla del grupo), se obtiene

(230)\[\begin{split} A_2 \rightarrow a_{A_2}=\frac{1}{6} \left(1 \times 1 \times 4 + 2 \times 1 \times 1 + 3 \times -1 \times 2\right) = 0\\ E \rightarrow a_{E}=\frac{1}{6} \left(1 \times 2 \times 4 + 2 \times -1 \times 1 + 3 \times 0 \times 2\right) = 1 \end{split}\]

Es decir, que la representación se puede descomponer en una suma de las siguientes irreps:

(231)\[D(R)=2A_1 + E \]

Para encontrar cada una de las combinaciones lineales de nuestra funciones de base que generan las irreps tendríamos que construir los proyectores dados por la Ec. (221), cuyo resultado son 3 matrices 4x4 y aplicarlos sobre los vectores de la base (ejercicio).

Simetría del Hamiltoniano

Después de todo el trabajo llevado a cabo anteriormente llegamos al punto clave del tema desde el punto de vista físico. Vamos a estudiar como que forma toma la matriz Hamiltoniana,

(232)\[h_{\alpha\beta}=\left\langle \psi_\alpha \right\vert \hat{h}\left\vert \psi_{\gamma}\right\rangle \]

cuando la evaluamos con orbitales simetrizados, es decir, cuando \(\psi_\alpha\) y \(\psi_\beta\) pertenecen a una irrep.

Primero observamos como se transforma el operador Hamiltoniano cuando le aplicamos una operación de simetría,

(233)\[\hat{O}\hat{h}=1\cdot\hat{h}\]

Independientemente de la operación de simetría que utilicemos, el operador de simetría por el Hamiltoniano es el propio Hamiltoniano por lo que todos los caracteres del Hamiltoniano son 1, es decir, el Hamiltoniano pertenece a la irrep totalmente simétrica (\(A_1\)).

Veamos ahora como se transforma la matriz Hamiltoniana, Ec. (232). Cuando apliquemos el operador de simetría este actuará, simultáneamente, sobre el Hamiltoniano y las funciones de onda,

(234)\[\begin{matrix} \hat{O} h_{\alpha\beta} =\left\langle \hat{O}\psi_\alpha \right\vert \hat{O}\hat{h}\left\vert \hat{O}\psi_{\gamma}\right\rangle \end{matrix}\]

Por simplicidad vamos a suponer que si las funciones de onda pertenecen a una irrep \(\gamma\) verifican,

(235)\[\hat{O}\psi_\gamma=o_\gamma \psi_\gamma\]

lo que sólo es válido en grupos abelianos (sin degeneración) donde los caracteres de todas las irreps son 1 o -1. Cuando se discuta que integrales se anulan por simetría probaremos este resultado desde un punto de vista más general.

Dado que el Hamiltoniano no cambia bajo las operaciones de simetría su matriz tampoco debiera hacerlo, por lo que obtenemos,

(236)\[\begin{matrix} \hat{O} h_{\alpha\beta} = h_{\alpha\beta} = o_\alpha^* o_\beta \left\langle \psi_\alpha \right\vert \hat{O}\hat{h}\left\vert \psi_{\gamma}\right\rangle = o_\alpha^* o_\beta \left\langle \psi_\alpha \right\vert \hat{h}\left\vert \psi_{\gamma}\right\rangle=o_\alpha^* o_\beta h_{\alpha\beta} \end{matrix}\]

La anterior ecuación tiene dos soluciones,

(237)\[\begin{split}\begin{matrix} \text{si} &h_{\alpha\beta}\neq 0 \rightarrow &o_\alpha^* o_\beta=1 \\ \text{si} & h_{\alpha\beta}= 0 \rightarrow & o_\alpha^* o_\beta~~ \text{no definido} \end{matrix}\end{split}\]

Es decir, que para que el elemento de matriz \(h_{\alpha\beta}\) sea no nulo el producto de los caracteres de las irreps de \(\psi_\alpha\) y \(\psi_\beta\) tienen que ser 1. Dado que la condición anterior se tiene que verificar para todas las operaciones de simetría eso quiere decir que los caracteres \(o_\alpha\) y o \(o_\beta\) tienen que ser siempre iguales y, por tanto, (dado que sólo pueden ser 1 o -1) que pertenecen a la misma irrep.

Es decir, que si se utilizan funciones simetrizadas para evaluar la matriz hamiltoniana esta tiene la forma por cajas mostrada en la Fig. 145, donde cada caja pertenece a una irrep.

Fig. 145 Forma del Hamiltoniano (matriz por cajas) cuando se expresa en una base simetrizada donde cada función de base pertenece a una irrep.

Hamiltonianos de la forma mostrada más arriba permiten reducir la dimensión de las matrices a diagonalizar el Hamiltoniano, lo que nos permitirá resolver analíticamente algunos problemas en moléculas sencillas y ayudan a comprender los procesos físicos que ocurren en moléculas más complejas.

Problemas y ejemplos