Estructura molecular

En esta sección empezaremos indicando como dar la geometría de una molécula (esto será algo muy sencillo) y procederemos a introducir las operaciones de simetría como una importante característica asociada a la forma de la molécula.

Geometría molecular

Para dar la geometría de la molécula se suelen utilizar coordenadas cartesianas en unidades adecuadas (normalmente angstrom (Å) o bohr). Así por ejemplo en la Fig. 14 se muestra la geometría del benceno y sus coordenadas en un formato muy usual llamado xyz. Existen otras maneras de dar la geometría de una molécula como la Z-matrix pero no van a ser importantes en este curso.

Fig. 14 (Derecha) Estructura del benceno obtenida mediante una simulación de primeros principios. Consiste en dos hexágonos colocados concéntricamente, el más interno formado de átomos de carbono y el segundo de átomos de hidrógeno. (Izquierda) Coordenadas de los 12 átomos utilizando coordenadas cartesianas y angstrom (10\(^{-10}\)m) como unidades de distancia.

Usualmente hay algunas convenciones que se utilizan para dar la geometría de una molécula. La más importante es que el eje z debe de coincidir con el eje de rotación de mayor orden de la molécula. También se suele hacer coincidir los ejes de la representación con los ejes principales del tensor de inercia de la molécula.

Operaciones de simetría

Vamos ahora a introducir las operaciones de simetría, que tendrán un papel central cuando queramos resolver el Hamiltoniano electrónico en una molécula (ver Simetría). La definición que se da más abajo no es la más general que puede haber (hay otras basadas en permutaciones que son muy potentes) pero, para trabajar bajo la aproximación adiabática, es la más práctica.

Definición: Una operación de simetría es un cambio en la geometría de la molécula que deja invariante su Hamiltoniano electrónico.

Es decir, si \(\hat{O}\) es un operador que cambia la geometría de una molécula de las coordenadas \(\vec{R}\) a las \(\vec{R}^\prime\) se dice que es de simetría si,

(33)\[\hat{O}\hat{H}_{el}(\vec{R})=\hat{H}_{el}(\vec{R}^\prime)=\hat{H}_{el}(\vec{R}).\]

Aunque la definición parezca un poco abstracta en la práctica es sencilla de aplicar. Dado que los únicos operadores del Hamiltoniano electrónico que dependen de las coordenadas nucleares son los operadores de energía potencial electrón-núcleo y núcleo-núcleo lo que dice la definición es que estos no pueden cambiar cuando cambiemos las posiciones de los mismos. Está claro que si cambiamos la forma de la molécula estas energías serán diferentes por lo que la única posibilidad de que el Hamiltoniano no cambie es intercambiar las posiciones de núcleos equivalentes. Esto se ve claramente en la Fig. 15 de una molécula hexagonal. Si intercambiamos cualquier par de átomos verdes entre sí la geometría habrá cambiado (los núcleos, que tratamos como partículas distinguibles, se han movido) pero el Hamiltoniano sigue siendo el mismo.

Fig. 15 Una estructura molecular hexagonal, similar al benceno pero aún más sencilla.

En lo que sigue daremos una clasificación estándar de las operaciones de simetría en moléculas (también se utilizan en sólidos) y, para ilustrar su efecto, utilizaremos una sencilla molécula ilustrada en la Fig. 16, donde hemos identificado la geometría inicial de la molécula etiquetando cada uno los átomos con un número. Es importante darse cuenta de que no todas las moléculas tienen todas las operaciones de simetría y que la presencia (o ausencia) de una de ellas puede tener importantes repercusiones en las propiedades de un compuesto.

Fig. 16 Una molécula idealizada sencilla con la forma de un cuadrado. Se han añadido etiquetas numéricas a los átomos para seguir como se introducen las operaciones de simetría.

Warning

La notación que vamos a seguir para las operaciones de simetría en moléculas es la de Schönflies, que es la más utilizada en este campo (y en la química). Existen otras notaciones posibles, como la de Hermann-Mauguin que es la dominante para los sólidos y que utilizaremos para trabajar con cristales.

¡Es muy importante saber utilizar ambas, cada una en su ámbito!

Inversión

La inversión, denotada mediante el símbolo \(i\), consiste en una operación que toma la posición de un átomo y le cambia el signo a todas sus componentes:

(34)\[\vec{R}_\alpha \rightarrow -\vec{R}_\alpha\]

Si nos fijamos en la Fig. 17 el centro de inversión está en medio del cuadrado. Su efecto es cambiar las posiciones de la siguiente manera:

\[\begin{split}1 \rightarrow 3\\2 \rightarrow 4\\ 3 \rightarrow 1\\ 4 \rightarrow 2\end{split}\]

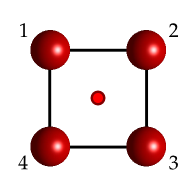
Fig. 17 Una molécula idealizada sencilla con la forma de un cuadrado mostrando el centro de inversión en su centro mediante un punto rojo.

Rotaciones

Una rotación de orden n, denotada mediante el símbolo \(C_n\), consiste en un giro alrededor de un cierto eje de un ángulo \(2\pi/n\) que hace que la molécula rotada coincida con la inicial. El sentido del giro es que viene dado por la regla de la mano derecha(Fig. 18), es decir, ángulos positivos son antihorarios.

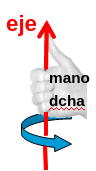
Fig. 18 Cuando se giran las moléculas, para determinar el sentido de giro se debe utilizar la regla de la mano derecha que indica que los ángulos positivos giran en sentido contrario a las agujas del reloj.

Volviendo al ejemplo de la molécula cuadrada la Fig. 19 ilustra un giro negativo asociado al eje de orden 4 (\(C_4\)) que pasa por el centro de la molécula. Los giros de \(\pm 2\pi/4\) tendría los siguientes efectos en la molécula:

\[\begin{split} \begin{matrix}-2\pi/4 &~~~~& +2\pi/4 \\ 1 \rightarrow 2 &~~~~& 1 \rightarrow 4 \\2 \rightarrow 3 &~~~~& 2 \rightarrow 1\\ 3 \rightarrow 4 &~~~~& 3 \rightarrow 2\\ 4 \rightarrow 1 &~~~~& 4 \rightarrow 3\end{matrix}\end{split}\]

Fig. 19 Una molécula idealizada sencilla con la forma de un cuadrado mostrando su eje de orden 4 central (el giro ilustrado sería negativo).

Esta molécula tiene otros ejes de rotación, como por ejemplo de orden 2 que unen los centros de aristas opuestas o los vértices. Aunque hay varios de estos ejes ninguno de ellos es el principal, que es el eje \(C_4\) (único) que es perpendicular al plano de la molécula y que pasa por su centro.

Convenio de ejes

El eje de rotación de mayor orden de una molécula se denomina eje principal de simetría y, por convenio, siempre se sitúa sobre el eje z.

Además se suele situar al eje x de una molécula siguiendo las siguientes reglas:

• Si la molécula es plana con z en el plano: El eje x será perpendicular al plano

• Si la molécula es plana con z perpendicular al plano: El eje x estará en el plano y se escogerá de modo que contenga al mayor número de átomos posible.

Planos de reflexión

Un plano de reflexión actúa como un espejo, intercambiando las posiciones de átomos que están en lados opuestos del mismo.

Si los planos de reflexión contienen al eje principal se dice que son verticales y se denotan como \(\sigma_v\), mientras que si son perpendiculares al mismo se dice que son horizontales y se denotan como \(\sigma_h\). Si un plano vertical además bisecta dos ejes \(C_2\) se dice que es diédrico. Estos conceptos se encuentran ilustrados en la Fig. 20.

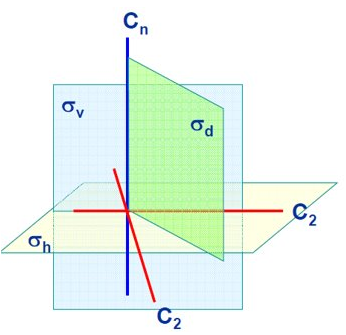
Fig. 20 Ilustración de los diferentes tipos de planos de reflexión en una molécula: verticales, horizontales y diédricos.

Veamos ahora el efecto de los diferentes planos en la molécula cuadrada. En las Fig. 21 y Fig. 22 las líneas verdes muestran dos planos de reflexión.

\[\begin{split}\begin{matrix}1 \rightarrow 2\\2 \rightarrow 1\\ 3 \rightarrow 4\\ 4 \rightarrow 3\end{matrix}\end{split}\]

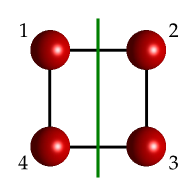
Fig. 21 Una molécula idealizada sencilla con la forma de un cuadrado mostrando un plano de reflexión (línea verde) que la parte a lo largo de la vertical. Dado que contiene al eje principal este eje es vertical.

\[\begin{split}\begin{matrix} 1 \rightarrow 1\\2 \rightarrow 4\\ 3 \rightarrow 3\\ 4 \rightarrow 2 \end{matrix}\end{split}\]

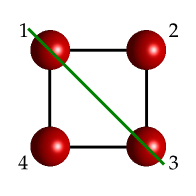
Fig. 22 Una molécula idealizada sencilla con la forma de un cuadrado mostrando un plano de reflexión (línea verde) que la parte a lo largo de la diagonal. Dado que contiene al eje principal este eje es vertical.

Ambos casos ilustrados en las figuras superiores son planos verticales (\(\sigma_v\)), dado que contienen al eje \(C_4\) que pasa por el centro de la molécula. Aún es más, ambos planos son diédricos ya que bisectan un par de ejes \(C_2\). Normalmente se suele decir que el primero es un plano vertical (también lo sería con el plano equivalente, que recorrería el eje x de la figura) mientras que el segundo es diédrico, de modo que se los pueda distinguir.

En cualquiera de las figuras podríamos también observar un plano horizontal (\(\sigma_h\)) que sería el plano del papel cuya transformación asociada sería,

\[\begin{split}1 \rightarrow 1\\2 \rightarrow 2\\ 3 \rightarrow 3\\ 4 \rightarrow 4\end{split}\]

Ejes impropios

Un eje impropio, denotado \(S_n\), es, en una molécula (en los sólidos la definición es ligeramente diferente), una combinación de una rotación de orden n con un plano de reflexión perpendicular al eje de rotación. Individualmente, ninguna de estas operaciones tiene por qué ser operación de simetría de la molécula pero, si el eje impropio está presente, su combinación sí lo será.

Este tipo de ejes está ilustrado para la molécula de etano en la Fig. 23. Aunque el eje impropio es de sexto orden (\(S_6\)) es claro que la molécula no tiene un eje de rotación (sencillo) de orden 6, tan sólo de orden 3. Tampoco tiene un plano de reflexión horizontal, que sería el plano turquesa ilustrado en la figura. Aún así, si giramos la molécula a lo largo de su eje principal \(2\pi/6\) y luego hacemos una reflexión tenemos que el giro alinea los átomos de hidrógeno a ambos lados de la molécula con los que la reflexión completa la operación de simetría.

Fig. 23 Eje impropio (roto-reflexión) S6 en la molécula de etano. Se muestra tanto el eje de rotación de orden 6 como una línea roja como el plano de reflexión que se aplica después en color turquesa.

Aunque esto será de más utilidad en los sólidos, es importante mencionar que la inversión es completamente equivalente a un eje \(S_2\), como puede apreciarse en la Fig. 24, mientras que una reflexión (trivialmente), es equivalente a una operación \(S_1\), como está ilustrado en la Fig. Fig. 25.

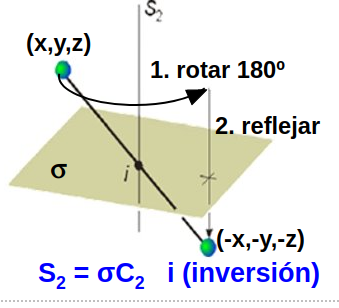
Fig. 24 Efecto de un eje de rotación S\(_2\), equivalente a la inversión.

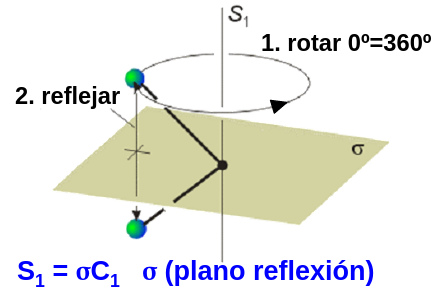
Fig. 25 Efecto de un eje de rotación S\(_1\), equivalente a la reflexión.

Problemas y ejemplos