Combinación Lineal de Orbitales Atómicos

Al discutir el método de Hartree-Fock decíamos que era un método variacional, donde la función de onda era un determinante de Slater, y variábamos la forma de los orbitales a un electrón que utilizábamos para construirlo. Este desarrollo, muy abstracto, no clarificaba (usábamos cálculo funcional) como podíamos variar la forma de los orbitales. En esta sección vamos a clarificar un método, el más usado y que más información física aporta, para ver como el principio variacional determina la forma de los orbitales moleculares (también se podría aplicar a un cristal) y da lugar al modelo de enlace fuerte o tight-binding.

En las ecuaciones de Hartree-Fock,

(145)\[\hat{h}\psi_i(\vec{r}) = \varepsilon_i \psi_i(\vec{r}).\]

que eran ecuaciones de Schrödinger para cada uno de los electrones en una molécula, aparecen unos autovectores, \(\psi_i\), que llamamos orbitales moleculares y que tienen unas energías, \(\varepsilon_i\) que vamos a denominar niveles moleculares.

Como ya indicábamos en la sección sobre Hartree-Fock, los orbitales moleculares se pueden escribir como el producto de una parte espacial, \(\phi_i(\vec{r})\), y otra de espín, \(\sigma_i\).

(146)\[\psi_i(\vec{r})=\phi_i(\vec{r})\sigma_i\]

La variación de la forma del orbital molecular se encierra en la parte espacial, \(\phi_i\). En un principio no sabemos que forma tiene esta función pero, parece lógico, que cuando nos encontremos cerca de un átomo esta función se parezca bastante al orbital atómico de ese átomo. Una manera sencilla de generar este comportamiento es escribir los orbitales moleculares como una combinación lineal de orbitales atómicos que denominaremos con sus siglas en inglés, LCAO (Linear Combination of Atomic Orbitals). Si denominamos al orbital atómico j con la letra \(\chi_j\) podemos escribir el orbital molecular i del siguiente modo,

(147)\[\phi_i(\vec{r}) = \sum_j c_{ij}\chi_j(\vec{r})\]

donde \(c_{ij}\) son los coeficientes numéricos que determinan exactamente la combinación lineal y que, por tanto, modifican la forma del orbital. Es decir, en Hartree-Fock cuando minimizamos la energía cambiando la forma de los orbitales, realmente lo que hacemos es variar la energía en función de los coeficientes \(c_{ij}\) que relacionan la composición del orbital molecular i con el orbital atómico j.

La Ec. (147) puede entenderse como la expansión de una función en una base, que pueden ser orbitales atómicos o de cualquier otro tipo. Si esa base es completa, es decir, permite expresar de forma exacta cualquier función, tendríamos el mínimo de energía posible para Hartree-Fock. Esto sólo es posible si incluimos todos los orbitales atómicos (en realidad esa base estaría sobredeterminada, ya que el espacio de Gilbert está definido por todas las soluciones de uno sólo de los átomos) lo que, en la práctica no es posible. En general, vamos a truncar el número de funciones que tenemos en cuenta en la Ec. (147) a una base mínima que nos permita entender el comportamiento de los enlaces entre átomos, aunque debemos saber que, numéricamente, esa solución no va a ser muy precisa.

La molécula más sencilla

La molécula más sencilla es el ión \(H_2^+\) que cuenta con dos núcleos de hidrógeno y un sólo electrón.

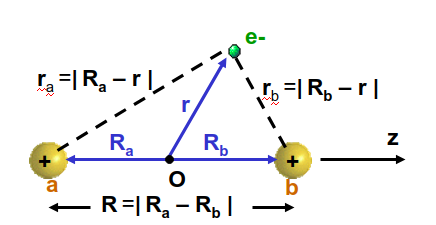
Fig. 104 Diagrama de las distancias importantes para resolver la ecuación de Schrödinger electrónica para el ión H\(_2^+\).

Su Hamiltoniano es,

(148)\[H_e = -\frac{1}{2}\vec{\nabla}^2-\frac{1}{\vert \vec{R}_a -\vec{r}\vert}-\frac{1}{\vert \vec{R}_b -\vec{r}\vert}+\frac{1}{\vert \vec{R}_a -\vec{R}_b\vert}\]

Dado que esta ecuación electrónica tan sólo implica un electrón es posible resolverla analíticamente. Incluso en esta sencilla molécula, donde el momento angular se conserva en el eje principal de la molécula, es complejo encontrar esta solución, que se encuentra, por ejemplo, en el libro de Slater [7]. El mensaje principal es que este tipo de resolución de la ecuación diferencial general no se puede realizar en problemas más complejos que contienen 2 o más electrones o con geometrías más complejas (3 o más núcleos). Eso implica que, si queremos encontrar un método general de describir la estructura electrónica de las moléculas tendremos que abandonar estas técnicas directas.

Orbitales atómicos

Los orbitales atómicos que vamos a tomar son las soluciones de la ecuación de Schrödinger para el átomo de hidrógeno. Estas se pueden escribir,

(149)\[\chi_{nlm}(\vec{r}) = R_{nl}(r) Y_{l}^{m}(\theta,\phi)\]

como el producto de una parte radial, \(R_{nl}\), que depende del número cuántico principal, \(n\), y del módulo del momento angular, \(l\), multiplicada por otra parte angular, \(Y_{l}^{m}\), dada por un armónico esférico, dependiente del módulo del momento angular, \(l\), y su proyección sobre el eje z, \(m\).

Parte radial

La parte radial de una función de onda hidrogenoide es[4] [11],

(150)\[R_{nl}(r) =C r^l L_{n-l-1}^{2l+1} e^{-\alpha r}\]

donde C es una constante de normalización, \(L_{n-l-1}^{2l+1}\) es el polinomio generalizado de Laguerre y \(\alpha\) es una constante de decaimiento que, en el átomo de hidrógeno, tiene el valor \(\alpha=2/na_0^\star\) donde \(a_0^\star\) es el radio de Bohr reducido, \(a_0^\star=4\pi\varepsilon_0 \hbar^2/\mu e^2\) y \(\mu\) es la masa reducida.

Las dos propiedades más importantes de la función atómica radial son:

• Decaimiento exponencial: La distribución de probabilidad radial en un átomo decae rápidamente y hace que los electrones estén localizados cerca del átomo. Cuanto mayor sea el número cuántico principal más pequeño será \(\alpha\) y más lento decaerá la densidad electrónica. En el átomo de hidrógeno el máximo de probabilidad radial depende exclusivamente del número cuántico principal, \(n\).

• Nodos: La distribución de probabilidad asociada a una función radial tiene \(n-l-1\) nodos. El número de nodos de la función atómica representa la energía cinética de los electrones, dado que este operador (ver Ec. (131)) mide la curvatura de la función de onda y, a mayor número de nodos, mayor curvatura y energía cinética.

En la Fig. 105 se muestran algunas funciones radiales y la densidad electrónica asociada a los mismos. Nótese el número de nodos dependiendo de \(n\) y \(l\).

Fig. 105 Diagrama mostrando el decaimiento de la parte radial de los orbitales atómicos para diferentes valores de \(n\) y \(l\) (izquierda) y la densidad radial de carga(derecha).

Parte angular

La parte angular de la función de onda atómica es un armónico esférico, \(Y_{l}^{m}\). Estas funciones representan el momento angular orbital que tiene el electrón en este orbital. Estas funciones de onda son, en general, complejas y se representan gráficamente en la Fig. 106.

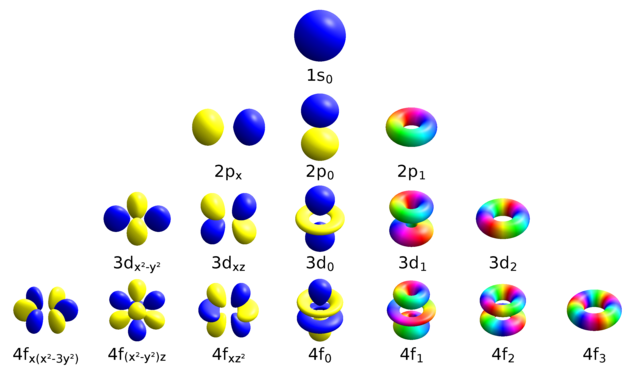
Fig. 106 Diagrama ilustrando la parte angular de los orbitales atómicos hidrogenoides. Se muestran tanto como orbitales reales como imaginarios. En los reales los colores azul y amarillo denotan, respectivamente, fases positivas y negativas de las funciones de onda. En los imaginarios la fase cambia de forma continua y esto se muestra con un mapa de color (C) Wikipedia.

Dado que la energía de los niveles atómicos depende sólo de \(n\) y \(l\), cuando se cambia el valor de \(m\) (desde \(m=-l\) hasta \(m=l\)) la energía no varía, es decir, hay \(2l+1\) niveles degenerados. Dado que si dos niveles están degenerados la combinación lineal de ambos también es solución de la ecuación de Schrödinger podemos escribir armónicos esféricos reales que son combinación lineal de los armónicos esféricos.

Por ejemplo, los orbitales p reales son,

(151)\[p_z=p_0 ~~~~ p_x=R_{21}\sqrt{\frac{1}{2}}(Y_1^{-1})-Y_1^1) ~~~~ d_{yz}=R_{32}i\sqrt{\frac{1}{2}}(Y_2^{-1})+Y_2^1)\]

mientras que los d son,

(152)\[d_{xy}=i\sqrt{\frac{1}{2}}\left(Y_{1}^{-2}-Y_{1}^{2}\right)=\frac{1}{2r^2}\sqrt{\frac{15}{\pi}}xy ~~~ d_{yz}=i\sqrt{\frac{1}{2}}\left(Y_{1}^{-1}+Y_{1}^{1}\right)=\frac{1}{2r^2}\sqrt{\frac{15}{\pi}}yz ~~~ d_{z^2}=Y_{2}^{0}=\frac{1}{4r^2}\sqrt{\frac{5}{\pi}}\left( 3z^2-r^2 \right) ~~~ d_{xz}=i\sqrt{\frac{1}{2}}\left(Y_{2}^{-1}-Y_{2}^{1}\right)=\frac{1}{2r^2}\sqrt{\frac{15}{\pi}}zx ~~~ d_{x^2-y^2}=\sqrt{\frac{1}{2}}\left(Y_{1}^{-2}+Y_{1}^{2}\right)=\frac{1}{4r^2}\sqrt{\frac{15}{\pi}}\left(x^2-y^2\right)\]

Es decir, podemos ver que el orbital \(p_x\) es proporcional a \(x\), mientras que el \(xy\) es proporcional, precisamente, a este producto de coordenadas (es decir, \(xy\)). En la Fig. 107 se muestra la forma de la distribución de probabilidad de algunos orbitales esféricos reales. Es importante darse cuenta que, al igual que en los orbitales radiales, los orbitales vienen caracterizados por un número de nodos que depende del momento angular, \(l\), un mayor número de nodos se corresponde con un mayor momento angular.

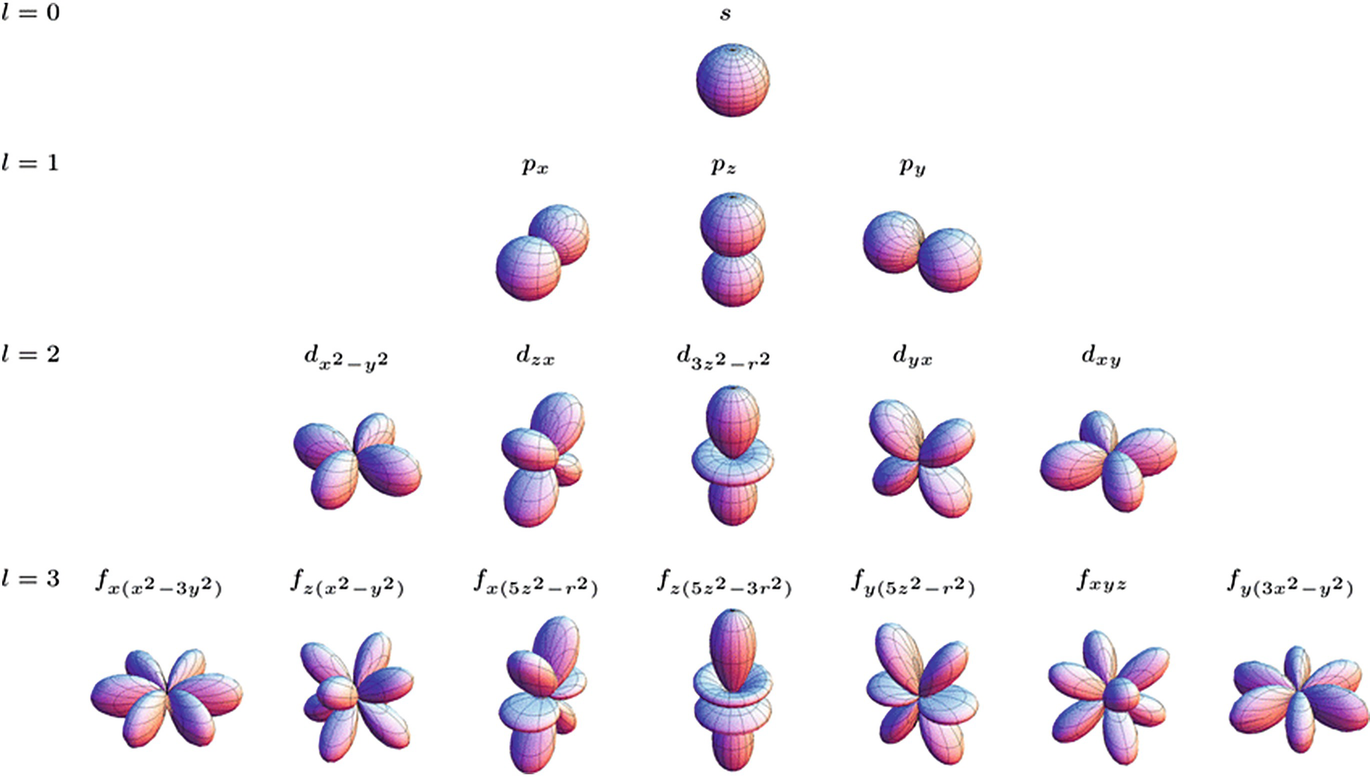
Fig. 107 Diagrama ilustrando la parte angular de los orbitales atómicos hidrogenoides en forma real. (C) Wikipedia.

Además de la densidad electrónica, es importante tener en cuenta la fase de los lóbulos de los orbitales atómicos y como están orientados con respecto a los ejes (ver Fig. 108). Esto será crucial cuando intentemos explicar el enlace entre átomos.

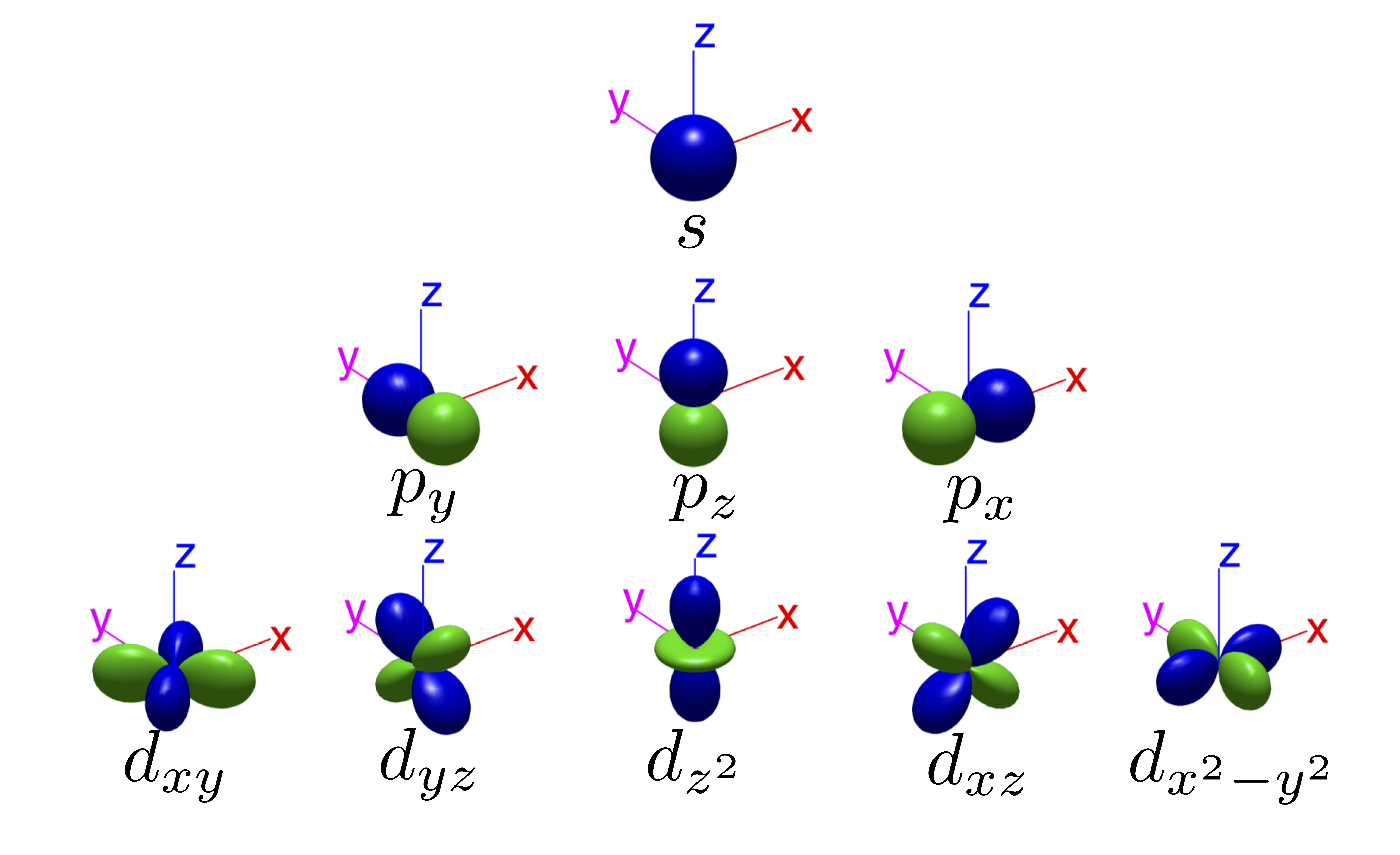
Fig. 108 Diagrama mostrando los orbitales atómicos reales y como se alinean con los ejes.

Resolución del problema de los orbitales moleculares

En Hartree-Fock discutimos como, al minimizar la energía asociada a un determinante de Slater con respecto a la forma de los orbitales moleculares \(\psi_i\) (o su parte espacial \(\phi_i\)), llegábamos a las ecuaciones de Hartree-Fock,

(153)\[\hat{h}\left\vert\psi_i\right\rangle=\varepsilon_i\left\vert\psi_i\right\rangle\]

Veamos, ahora, como resolverlas con ayuda de las LCAO Ec. (147). Para ello escribimos el ket asociado a un orbital molecular como una combinación de orbitales atómicos,

(154)\[\left\vert\psi_i\right\rangle=\sum_a c_{ia}\left\vert\chi_a\right\rangle.\]

Ahora sustituimos la Ec. (154) en la ecuación de Hartree-Fock, Ec. (153) y multiplicamos por la derecha por el bra, \(\left\langle \chi_b \right\vert\),

(155)\[\left\langle \chi_b \right\vert \hat{h} \sum_a c_{ia}\left\vert\chi_a\right\rangle = \varepsilon_i \left\langle \chi_b \right\vert \sum_a c_{ia} \left\vert \chi_a \right\rangle \longrightarrow \sum_a c_{ia} \left\langle \chi_b \right\vert \hat{h} \left\vert\chi_a\right\rangle = \varepsilon_i \sum_a c_{ia} \left\langle \chi_b \right. \left\vert \chi_a \right\rangle\]

Podemos identificar ahora la matriz hamiltoniana,

(156)\[h_{ab}=\left\langle \chi_a \right\vert \hat{h} \left\vert \chi_b \right\rangle\]

y la matriz de solape entre dos orbitales atómicos,

(157)\[S_{ab}= \left\langle \chi_b \right. \left\vert \chi_a \right\rangle\]

que mide cuanto se superponen ambos orbitales en el espacio y es una medida tanto de la ortogonalidad de los orbitales atómicos (el solape es 0 si los orbitales son ortogonales) además de como de fuerte será su interacción.

Con ello llegamos a una ecuación matricial, llamada de Roothan- Hartree-Fock,

(158)\[\sum_a c_{ia} h_{ab} = \varepsilon_i \sum_a c_{ia} S_{ab}\]

que puede identificarse como un problema de autovalores generalizado,

(159)\[\hat{h}\vec{c}_i = \varepsilon_i \hat{S} \vec{c}_i.\]

Es decir, que para encontrar los niveles moleculares y sus funciones de onda lo que debemos hacer es diagonalizar la matriz hamiltoniana, teniendo cierto cuidado con la matriz de solape.

La matriz hamiltoniana

En la base de los orbitales atómicos el operador hamiltoniano a un electrón viene representado por la matriz de la Ec. (156). En este Hamiltoniano hay dos tipos de elementos bien diferenciados:

• Elementos diagonales: Tiene la siguiente expresión,

(160)\[h_{aa}=\left\langle \chi_a \right\vert \hat{h} \left\vert \chi_a \right\rangle = \varepsilon_a\]

y miden la energía que tendría el orbital atómico dentro de la molécula. Hay que tener en cuenta que el hamiltoniano electrónico dado por las ecuaciones de Hartree-Fock tiene más componentes que el Hamiltoniano del átomo al que pertenece el orbital \(a\) y, por tanto, esta energía no es, tan sólo, la energía atómica si no que esta se ve corregida, por ejemplo, por la presencia del resto de los núcleos (y electrones) de la molécula.

• Elementos no diagonales: A veces conocidos como elementos de hopping (salto),

(161)\[h_{ab}=\left\langle \chi_a \right\vert \hat{h} \left\vert \chi_b \right\rangle = \gamma_{ab}\]

dado que indican la facilidad que tiene un electrón que está en el orbital \(\chi_a\) para viajar al orbital \(\chi_b\). Como se verá en el ejemplo de la molécula del \(H_2\) más abajo, los elementos de hopping son, en una aproximación grosera, proporcionales a la integral de solape. Dado que la densidad radial de los orbitales atómicos decae exponencialmente esto nos permite deducir que, en general, los elementos de hopping serán de corto alcance, pudiendo despreciarse cuando los átomos están muy separados.

Ejemplo: La molécula de \(H_2\)

Veamos aquí la aplicación más sencilla de la teoría LCAO presentada más arriba, en la molécula de \(H_2\). Vamos a considerar una molécula de hidrógeno donde los átomos están separados por la distancia experimental de equilibrio, \(R=1.07Å\). Como base para escribir la LCAO vamos a tomar un orbital 1s de hidrógeno sobre cada uno de los átomos (es decir, dos orbitales 1s en total, representados por esferas azules en la Fig. 109) que denominaremos \(\chi_a\) y \(\chi_b\).

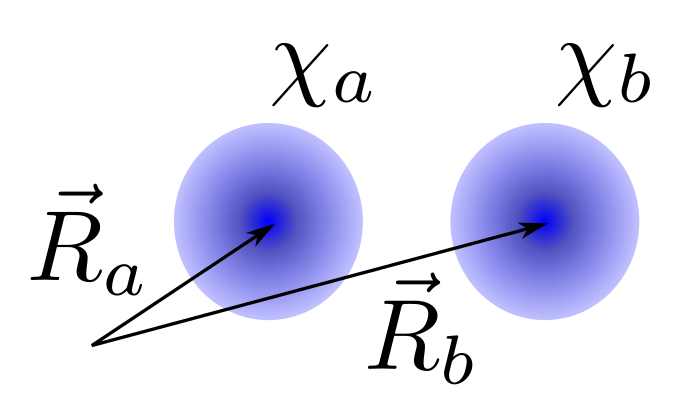
Fig. 109 Posiciones de los orbitales 1s en la molécula de H\(_2\) centrado, cada uno, alrededor de un núcleo (a y b) de la molécula.

Los orbitales atómicos del hidrogeno están normalizados, por lo que,

(162)\[S_{aa}=S_{bb}=1\]

Utilizando la expresión Ec. (150) de los orbitales atómicos 1s se llega al solape entre las funciones \(\chi_a\) y \(\chi_b\),

(163)\[S=S_{ab}=S_{ba}=e^{-R}\left(1+R+\frac{R^2}{3}\right)\]

Dado que los dos átomos de hidrógeno son equivalentes, podemos evaluar los elementos diagonales,

(164)\[\varepsilon_H=h_{aa}=h_{bb}=E_H+\frac{1}{R}-J\]

y los no diagonales del Hamiltoniano,

(165)\[\gamma=h_{ab}=h_{ba}=E_HS+\frac{1}{R}S-K\]

En las expresiones anteriores \(E_H\) es la energía atómica del orbital 1s del hidrógeno (-13.6 eV) mientras que,

(166)\[J=\left\langle \chi_a \right\vert \frac{1}{\vert \vec{r}-\vec{R}_b\vert}\left\vert\chi_a\right\rangle = -E_H\frac{2}{R}\left[1-e^{-2R}(1+R)\right]>0\]

es la interacción electrón-nucleo sobre el mismo átomo y,

(167)\[K=\left\langle \chi_a \right\vert \frac{1}{\vert \vec{r}-\vec{R}_a\vert}\left\vert\chi_b\right\rangle = -E_H\frac{2}{R}\left[1-e^{-2R}(1+R)\right]>0.\]

es la interacción electrón nucleo que afecta al hopping. Podemos observar que los elementos diagonales tienen, lógicamente, el mismo valor, dado que los dos orbitales son completamente equivalentes. Del mismo modo los elementos no diagonales son también iguales, dado que el operador Hamiltoniano es hermítico (es decir, que si es real es simétrico).

Podemos ahora tomar la ecuación de Roothan-Hartree-Fock (Ec. (158)) y escribirla del siguiente modo,

(168)\[\hat{h}\vec{c}_i = \varepsilon_i \vec{S}\vec{c}_i \rightarrow \left(\hat{h}-\varepsilon_i \hat{S}\right)\vec{c}_i=0\]

Escribiendo explícitamente la ecuación matricial y sustituyendo los elementos diagonales por la energía modificada del orbital 1s del hidrógeno, \(\varepsilon_H\), y el hopping por \(\gamma\), se obtiene,

(169)\[\begin{split}\begin{pmatrix} h_{aa}-\varepsilon_i S_{aa} & h_{ab}-\varepsilon_i S_{ab}\\ h_{ba}-\varepsilon_i S_{ba} & h_{bb}-\varepsilon_i S_{bb} \end{pmatrix} \begin{pmatrix} c_{ia}\\ c_{ib} \end{pmatrix}=0 \Longrightarrow \begin{pmatrix} \varepsilon_H-\varepsilon_i & \gamma-\varepsilon_i S\\ \gamma-\varepsilon_i S & \varepsilon_H-\varepsilon_i \end{pmatrix} \begin{pmatrix} c_{ia}\\ c_{ib} \end{pmatrix}=0\end{split}\]

que tiene solución no trivial tan sólo si el determinante secular es no nulo, lo que permite encontrar los niveles de energía,

(170)\[\begin{split}\begin{vmatrix} \varepsilon_H-\varepsilon_i & \gamma-\varepsilon_i S\\ \gamma-\varepsilon_i S & \varepsilon_H-\varepsilon_i \end{vmatrix}=0 \Rightarrow \varepsilon_H-\varepsilon_i = \pm \left(\gamma-\varepsilon_iS\right)\end{split}\]

Por tanto, podemos ver que las energías del nivel más profundo es,

(171)\[\varepsilon_0=\frac{\varepsilon_H +\gamma}{1+S}=E_H-\frac{J+K}{1+S}+\frac{1}{R}\]

mientras que el superior es,

(172)\[\varepsilon_1=\frac{\varepsilon_H -\gamma}{1-S}=E_H-\frac{J-K}{1-S}+\frac{1}{R}\]

donde vemos que los niveles moleculares tienen como energía base la energía del orbital atómico en el átomo aislado, \(E_H\), que se ve corregido por la integrales de interacción electrón nucleo J y K y la separación entre los átomos, R. Una representación gráfica de como se colocan los niveles moleculares respecto a los atómicos se muestra en la Fig. 110.

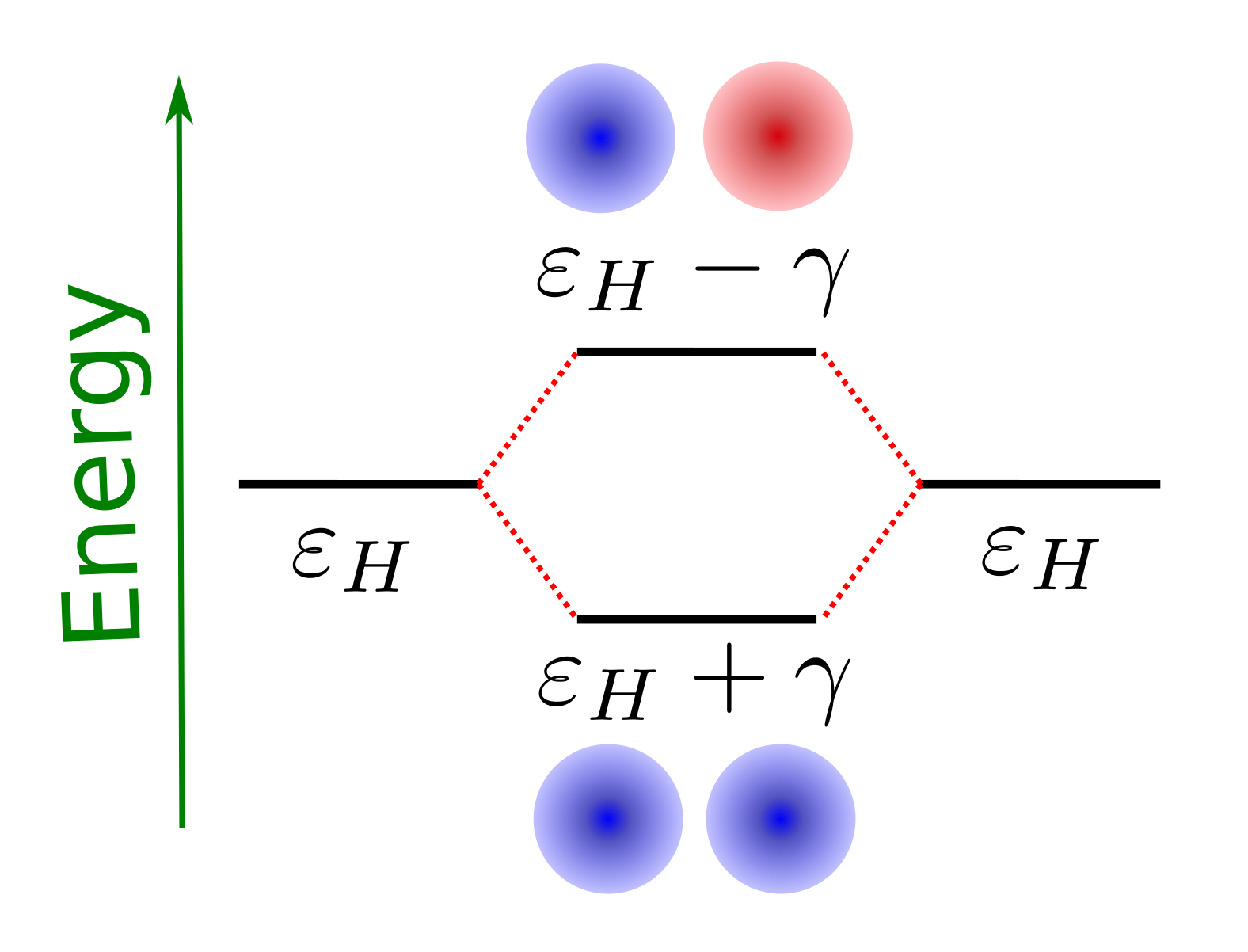
Fig. 110 El diagrama de niveles de la molécula de H\(_2\) neutra.

Estos niveles se discutirán en mayor detalle en el tema de las moléculas diatómicas.

Tan sólo queda mencionar que los niveles moleculares se deben poblar con los electrones contenidos en los átomos que forman la molécula. Es decir, que si sólo hubiera un electrón (el ión H\(_2^+\)), se colocaría en el nivel inferior \(\varepsilon_0\). En la molécula de hidrógeno (ver Fig. 111) donde cada átomo de hidrógeno aporta un electrón, colocaremos los dos electrones con espines apareados (es decir, uno hacia arriba y otro hacia abajo) en el nivel inferior.

Fig. 111 El diagrama de niveles, con sus ocupaciones, de la molécula de H\(_2\) neutra.

Cuando haya más electrones en el sistema, como en la molécula de He\(_2\) (ver {numref}`EE_he2_ground´) habrá que ir colocando electrones empezando por el nivel de más baja energía y llenando hacia los niveles de más alta energía.

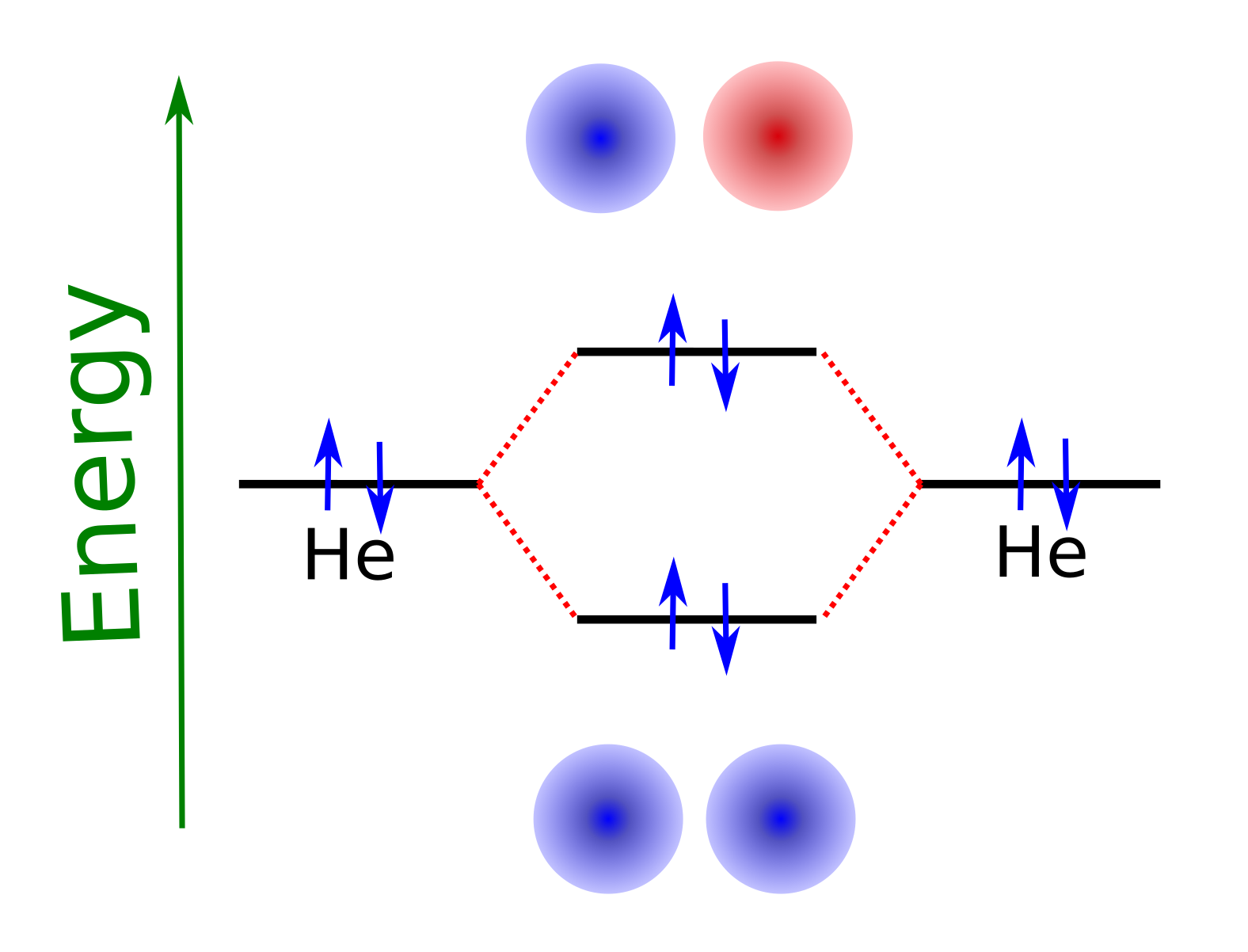
Fig. 112 El diagrama de niveles, con sus ocupaciones, de la molécula de He\(_2\) neutra.

Moléculas magnéticas

En un principio, siguiendo el principio de llenado dado en el ejemplo anterior las moléculas tenderán a tener espín \(S=0\) si tienen un número par de electrones y \(S=1\) si lo tuvieran impar. En realidad, esto no es así. Si consideramos un sistema con dos niveles, como el representado en la Fig. 113, que están separados por una energía \(\delta\) y dos electrones, estos se colocaran con sus espines apareados en un estado singlete de espín (\(S=0\)) o con sus espines desapareados en un estado triplete (\(S=1\)) dependiendo de la interacción entre ambos electrones.

Fig. 113 Esquema de niveles (izquierda) donde se muestran dos niveles separados por una energía \(\delta\). Energéticamente el estado no magnético con \(S=0\) (centro) es diferente al magnético con \(S=1\) (derecha).

Si los electrones no interaccionaran entre sí el estado fundamental sería el singlete. Aún así los electrones interaccionan entre sí y cambia dependiendo que se coloquen apareados o desapareados. En particular, cuando los electrones tienen el mismo espín (como en el estado triplete) el intercambio reduce su energía. Así, podemos ver que en el estado singlete la energía HF es,

(173)\[E_{HF}= 2 h_1 + J_{11}\]

donde \(h_1\) es la energía a un electrón (cinética más electrón núcleo) del orbital inferior, mientras que \(J_{11}\) es la interacción directa entre electrones situados en ese nivel. En cambio, la energía del estado triplete es,

(174)\[E_{HF}= h_1+h_2+J_{12}-K_{12}\]

donde \(h_2\), \(J_{12}\) y \(K_{12}\) son, respectivamente, la energía a un electrón del segundo nivel, la interacción directa entre un electrón en el nivel 1 y otro en el nivel 2 y la correspondiente interacción de intercambio. Si \(\delta\approx h_2-h_1\) es pequeño frente a las interacciones electrón-electrón es posible que el estado triplete sea el estado fundamental. Esto es típico en metales de transición donde las interacciones electrón-electrón son más importantes debido a que los orbitales 3d son internos y, por lo tanto, compactos.

Realmente, como la energía depende de como se colocan los electrones, las ecuaciones de Hartree-Fock hay que resolverlas de forma autoconsistente y eso hace que no sólo las energías electrón-electrón sean importantes. Precisos cálculos de primeros principios muestran como la energía electrón-núcleo estabiliza, de forma más importante que el intercambio, el estado triplete en átomos y moléculas.

Ejemplo: Estados singlete y triplete en \(H_2\)

En la molécula de hidrógeno la separación de los dos niveles inferiores es del orden de una decena de eV (ver Fig. 114). Esta separación es muy grande y mayor que las interacciones electrón-electrón (típicamente \(<\)1eV) que pudieran favorecer al triplete.

Fig. 114 El diagrama de niveles de la molécula de H\(_2\) donde no se ha tenido en cuenta la población de los niveles. Hay un orbital de baja energía donde ambos orbitales de hidrógeno están en fase y otro a más alta energía donde la combinación de los orbitales de hidrógeno es en contra fase.

Por tanto, el estado fundamental de la molécula de hidrógeno es el estado singlete (derecha) frente al estado triplete (izquierda).

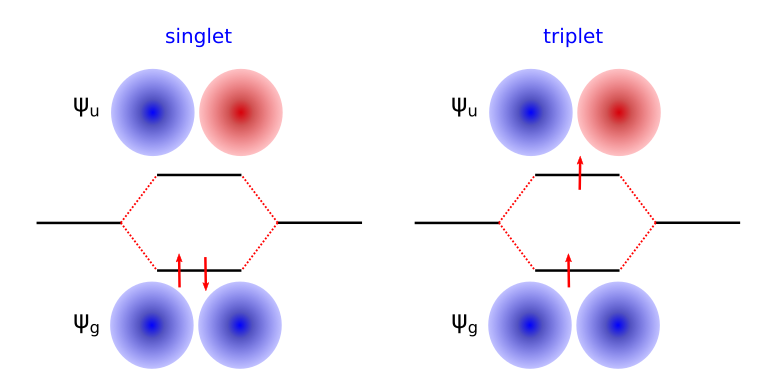
Fig. 115 Esquema de niveles para H\(_2\) neutro en sus configuraciones singlete (izquierda) y triplete (derecha).

Problemas y ejemplos