Primera zona de Brillouin#
En el apartado de estructuras cristalinas definimos la celda primitiva como aquella que contenía un único punto de red. De forma práctica hemos visualizado esta celda primitiva como el volumen interior del paralelepípedo que forman los vectores \(\vec{a}_1\), \(\vec{a}_2\) y \(\vec{a}_3\). Es importante notar que esta manera de tomar la celda primitiva no es única y hay otras maneras de encontrar la celda primitiva en el espacio real como, por ejemplo, la de Wigner-Seitz.
La primera zona de Brillouin, un concepto clave para desarrollar la física de los materiales cristalinos, va a ser, precisamente, el mismo concepto que el de la celda de Wigner-Seitz pero en el espacio recíproco.
Definición#
Definimos la celda de Brillouin o primera zona de Brillouin como aquella parte del espacio recíproco que se encuentra más cerca de un punto de la red recíproca (primitiva) que de cualquier otro.
Por definición esta estructura puede contener tan sólo 1 punto de red por lo que es primitiva. Por otro lado esta estructura puede tener una forma que no es sencilla (frente al paralelepípedo usual de la celda primitiva usual) pero, como ventaja, su forma será representativa de la simetría del sistema, en particular el sistema cristalográfico.
Matemáticamente este concepto está asociado a la aplicación de los diagramas de Voronoi al problema de las redes cristalinas.
Construcción#
El objetivo de la construcción de la primera zona de Brillouin es conseguir la región del espacio que está más cerca de un punto de la red recíproca que de cualquier otro. Partamos, por ejemplo, de la red periódica en dos dimensiones representada en la Fig. 75.

Fig. 75 Ejemplo de red bidimensional oblicua sencilla. Los puntos representan los puntos de la red recíproca del sistema y las líneas bordean las celdas “convencionales” de este sistema.#
Debemos seguir los siguientes pasos:
-1. Tomamos un punto de la red recíproca y trazamos líneas a todos sus vecinos cercanos.
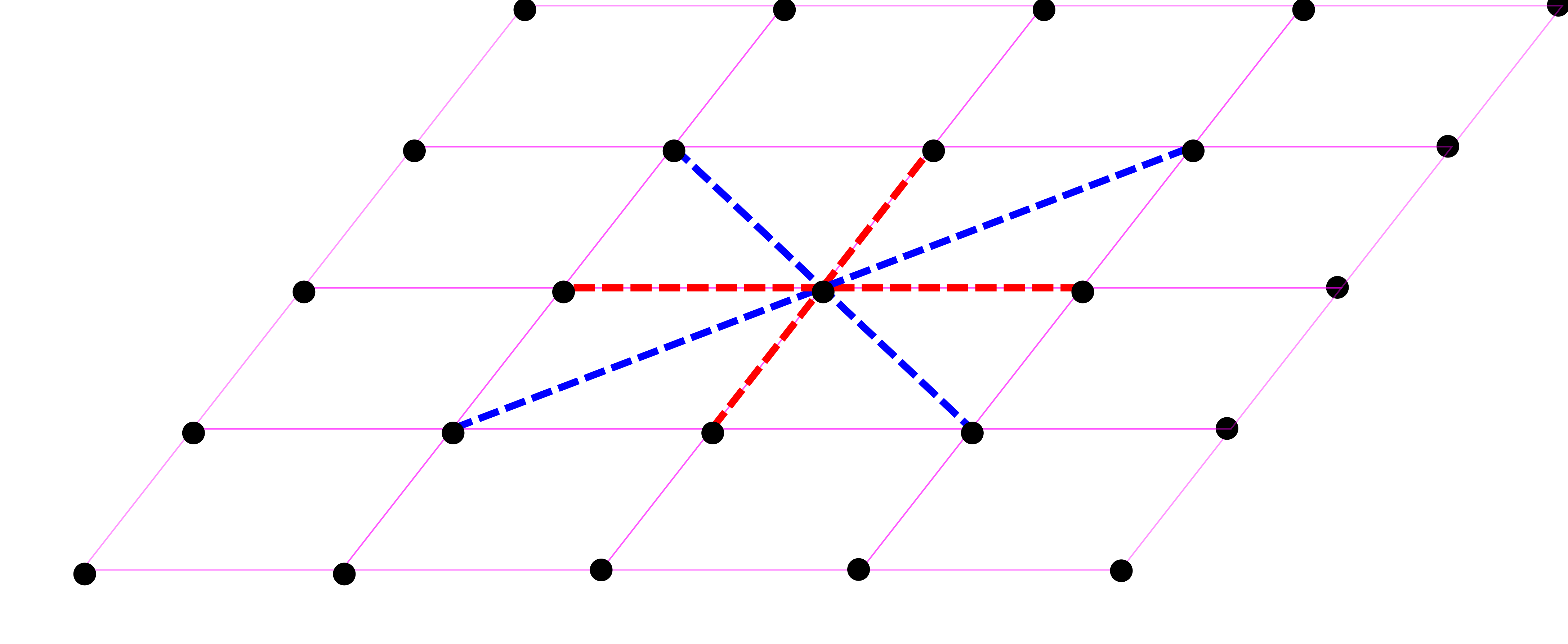
Fig. 76 El primer paso para representar la primera zona de Brillouin es unir un punto con sus vecinos más cercanos. En este caso estamos usando primeros vecinos en \(\vec{a}_1^\star\) y \vec{a}_2^\star$ (líneas rojas) y segundos (líneas azules)#
-2. Dibujamos la mediatriz de cada uno de estos segmentos. Esta línea separa la región del espacio que está más cerca del punto central del que está más cerca de sus vecinos.

Fig. 77 Las líneas verdes representan las mediatrices que separan las regiones más cercanas al punto central que a sus vecinos.#
-3. La primera zona de Brillouin es la región del espacio más cercana al punto central y limitada por varias de las mediatrices que se han representado.

Fig. 78 La figura central sombreada en verde y limitada por líneas negras es la primera zona de Brillouin. Nótese como si se traslada a cualquier otro punto de red se puede generar todo el espacio, por lo que se trata de una celda que puede usarse para describir el motivo de la red.#
Ejemplo
La utilidad de la primera zona de Brillouin se hará más clara en el tema de las vibraciones cristalinas. Veamos un caso sencillo para tener en mente lo importante de esta estructura en la descripción de los sólidos.
Imaginémosnos un sólido unidimensional con un átomo por motivo, tal y como se representa en la Fig. 79. Las interacciones entre los átomos, aunque tengan una naturaleza cuántica complicada, pueden imaginarse como si de muelles se trataran, ya que el movimiento de los átomos se realiza alrededor de su punto de equilibrio (aproximación armónica).
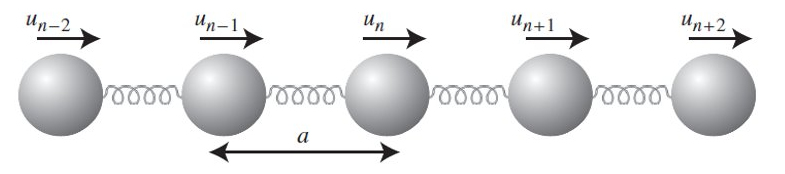
Fig. 79 Cadena lineal muelles#
El problema tiene N grados de libertad, donde N son los átomos del sólido. Evidentemente este número es muy grande y resolver el problema es complejo. Normalmente la manera de tratarlo es imaginarse que el sólido es infinito y periódico. Usando estas propiedades podemos representar (como se muestra en la Fig. 80) la variación de la energía con el vector de ondas de las vibraciones que, precisamente, se corresponde con vectores de la red recíproca en la primera zona de Brillouin.
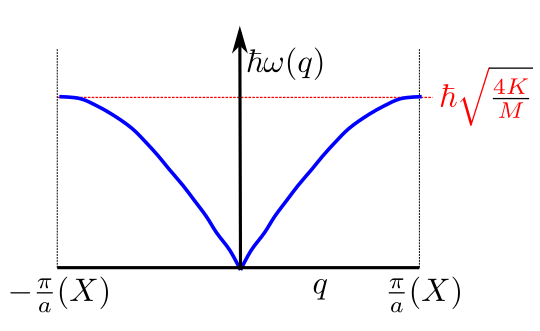
Fig. 80 Curvas de dispersión de las vibraciones en un sólido unidimensional con un átomo de motivo. Nótese que los puntos del eje X coinciden con los límites impuestos por la 1ª zona de Brillouin.#
Precisamente no es difícil ver como la primera zona de Brillouin en un sistema unidimensional va desde \(k=-\pi/a\) a \(\pi/a\) (es decir, que tiene la misma longitud que un vector de red de la red recíproca \(2\pi/a\), ver Fig. 81).
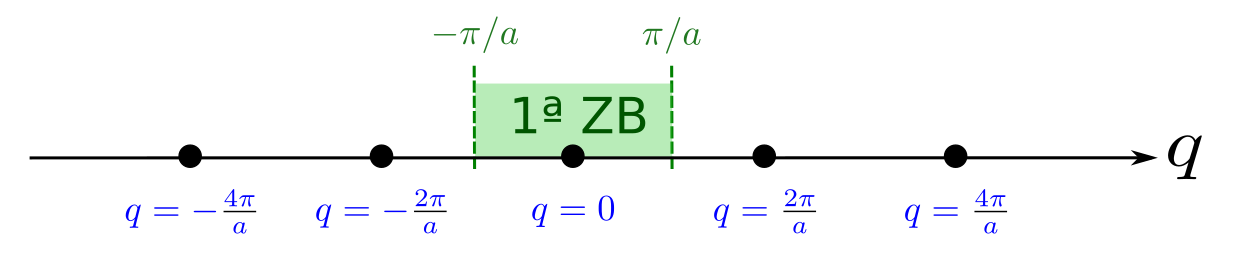
Fig. 81 Ilustración de la primera zona de Brillouin en un sistema unidimensional comparada con la popia red recíproca.#
Puntos especiales de la primera zona de Brillouin#
Cuando se estudien las propiedades físicas de un sólido cristalino, tanto en el caso de sus vibraciones como de sus bandas electrónicas (que se verán en el curso de física del estado sólido), es importante fijarse en algunos puntos especiales (que normalmente tienen alta simetría) de la primera zona de Brillouin. Por ejemplo en el caso del esquema Fig. 80 de dispersión de las bandas vibracionales de un sólido unidimensional, los puntos más importante son el central, que llamamos \(\Gamma\) (\(k=0\)) y el borde de zona, que llamamos \(X\) (\(k=\pm \pi/a\)).
Es importante ser capaz de dar las coordenadas de estos puntos. Para ello siempre usaremos la red recíproca convencional.
Ejemplo
La red recíproca de una celda cúbica F es una red cúbica I de parámetro de malla \(4\pi/a\). En la {numref}`rr_cubicF_points´ mostramos la primera zona de Brillouin de la misma junto con los puntos \(\Gamma\), L, X, W y K que son de alta simetría y, en muchos casos, importantes para describir la física de problemas con estas celdas.

Fig. 82 Ilustración de la primera zona de Brillouin de una red directa cúbica F (que es una red I en el espacio recíproco). Se muestran, mediante círculos rojos, puntos especiales de la 1ª zona de Brillouin. Para calcular las coordenadas de estos puntos es muy importante tener en cuenta el módulo de la red convencional recíproca, \(4\pi/a\) mostrado en la figura. En verde se muetra un plano ecuatorial que usaremos para dar las coordenadas de X, W y K.#
Deseamos conocer las coordenadas de estos puntos. Para ello recordamos que los vectores de red de la convencional son:
Usando la notación adecuada para puntos de la red recíproca (paréntesis) vemos que, en esta base, el punto \(\Gamma\) es el (0,0,0) que tiene simetría cúbica (\(O_h\)). El punto L es (\(\frac{1}{2}\),\(\frac{1}{2}\),\(\frac{1}{2}\)) y tiene simetría hexagonal (\(D_{6h}\)) ya que se encuentra en el centro de una cara hexagonal de la primera zona de Brillouin.
Para encontrar las coordenadas del resto de los puntos representamos el corte de la celda de Brillouin con el plano A en la Fig. 83.
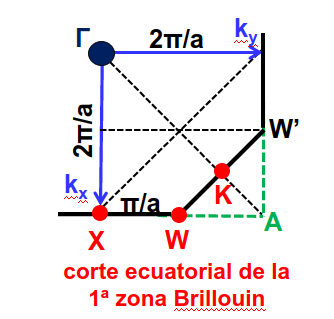
Fig. 83 Corte de la 1ª zona de Brillouin de una red directa cúbia F por el plano \(k_z=0\).#
Con ello es sencillo observar que las coordenadas son:
