Elementos de matriz

En este apartado empezaremos a conectar la resolución de las ecuaciones de Hartree-Fock y la teoría LCAO con la simetría. En particular, vamos a observar como, usando una base de orbitales atómicos, podemos expresar las operaciones de simetría. Esto nos va a llevar a representar los operadores mediantes matrices lo que nos va a permitir usar toda la potencia del álgebra de grupos en la siguiente sección. Es importante incidir también en el hecho que expresar los operadores como matrices es ideal para poder trabajar con ellos con ordenadores y es el principio para poder usar técnicas computacionales para resolver problemas de mecánica cuántica.

Grupo de las operaciones de simetría

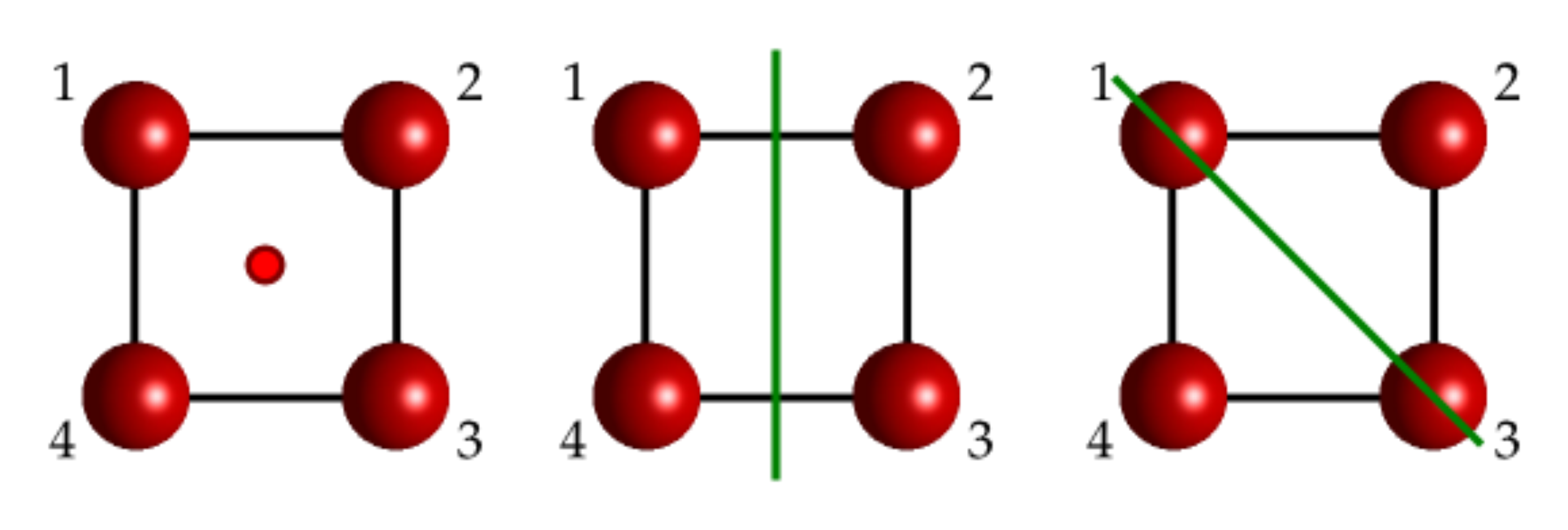
Fig. 121 Ilustración de algunas operaciones de simetría del grupo D\(_{4h}\) aplicadas sobre una molécula de 4 átomos cuadrada.

Tal y como se introducía en el apartado de grupos puntuales de moléculas, las operaciones de simetría forman un grupo. Es decir, cuando consideramos todas las operaciones de simetría de una molécula y su producto, que consistía en observar el efecto de aplicar una operación de simetría y luego otra sobre el resultado, se verificaban las siguientes propiedades:

• Conjunto cerrado: El producto de operaciones de simetría es una operación de simetría.

• Propiedad asociativa: Dadas tres operaciones \(A\), \(B\) y \(C\) se cumple que \(A\times(B\times C)=(A\times B)\times C\).

• Elemento neutro: La rotación de orden 1 no cambia el sistema y lo deja como al principio.

• Elemento inverso: Para toda operación siempre existe otra que devuelve el sistema a su configuración original

El objetivo de esta sección, y todo este capítulo, va a ser aplicar las propiedades de la teoría de grupos para ayudarnos en la resolución de la ecuaciones de Hartree-Fock.

Operaciones conjugadas y clases

Observando todas las operaciones de un sistema resulta evidente que hay operaciones de simetría que están muy relacionadas con otras. Por ejemplo, el plano de reflexión dibujado por una línea vertical en la Fig. 121 es completamente equivalente a dibujar la línea en horizontal. ¿Cómo lo sabemos? Por que si giramos 90\(^o\) el dibujo, otra de las operaciones de simetría del sistema, pasamos de un plano al otro.

Precisamente, la descripción dada más arriba coincide exactamente con la definición de operaciones conjugadas. Dos operaciones \(R_1\) y \(R_2\) se dicen conjugadas si existe una operación \(R_3\) tal que:

(195)\[R_3 R_2 R_3^{-1} = R_1\]

Para comprender la definición anterior es importante recordar que, al cambiar de sistema de referencia, una matriz \(A\) pasa a una \(A^\prime\) siguiendo el producto \(A^\prime=T A T^{-1}\), donde \(T\) es la matriz de transformación del sistema de coordenadas.

Todas las operaciones de simetría conjugadas entre sí forman una clase.

Ejemplo: Amoníaco

En el amoníaco (grupo D\(_{3h}\)) los planos de reflexión verticales están relacionados entre sí mediante las rotaciones del eje principal, de orden 3 (ver Fig. 122). Dado que no hay más operaciones conjugadas a estos 3 planos su conjunto forma una clase.

Fig. 122 Los planos de reflexión en el amoníaco están relacionados entre sí mediante el eje \(C_3\). Por ello, los planos se dice que están conjugados.

Representación matricial de funciones

Supongamos que queremos resolver las ecuaciones de Hartree Fock en una base de orbitales atómicos \(\{\chi\}\) compuesta por N funciones atómicas que llamaremos representación D. La parte espacial del orbital molecular \(\phi\) tiene la forma de una LCAO, que puede caracterizarse por el vector de los coeficientes atómicos,

(196)\[\begin{split}\vert \phi \rangle=c_1 \vert \chi_1 \rangle + c_2 \vert \chi_2 \rangle + \cdots c_N \vert \chi_N \rangle \rightarrow \vert \phi \rangle = \begin{pmatrix} c_1 \\ c_2 \\ \cdots \\ c_N\end{pmatrix}\end{split}\]

sabiendo que la base de orbitales atómicos es \(\{\vert \chi_1 \rangle, \vert \chi_2 \rangle, \cdots \vert \chi_N \rangle\}\).

Utilizando esta base también podemos representar cualquier operador, como hacíamos con el Hamiltoniano en el tema anterior, del siguiente modo,

(197)\[O_{ab}=\left\langle\chi_a\right\vert \hat{O} \left\vert \chi_b \right\rangle\]

La matriz anterior debe entenderse como:

• 1: Aplicamos el operador \(\hat{O}\) sobre el orbital \(\vert\chi_b\rangle\). Normalmente, esto cambiará de posición el orbital y lo rotará/reflejará.

• 2: Seguidamente realizaremos el solape entre la función \(\langle \chi_a \vert\) sobre el resultado de aplicar \(\hat{O}\) sobre \(\vert \chi_b \rangle\).

Gráficamente esto es sencillo de comprender, ver los ejemplos siguientes.

Ejemplo: funciones H(1s) en el Amoníaco

En este ejemplo vamos a suponer que tenemos las 3 funciones 1s que están centradas en los átomos de hidrógeno en el amoníaco. Nuestra base atómica es:

(198)\[\{s_1,s_2,s_3\}\]

Estas funciones están representadas por círculos negros, etiquetados adecuadamente, en la Fig. 123.

Fig. 123 Posición de los orbitales 1s de los hidrógenos del amoníaco marcados por las etiquetas \(s_1\), \(s_2\) y \(s_3\)

Si aplicamos la operación de simetría \(C_3^-\) (giramos en sentido horario), podemos ver que el orbital \(s_1\) pasa al \(s_3\) que, a su vez, pasa al \(s_2\) que se mueve donde estaba el \(s_1\) inicialmente (Fig. 124). En la figura podemos ver como el vector inicial \((c_1,c_2,c_3)\) después de la rotación pasa a ser el \((c_2,c_3,c_1)\)

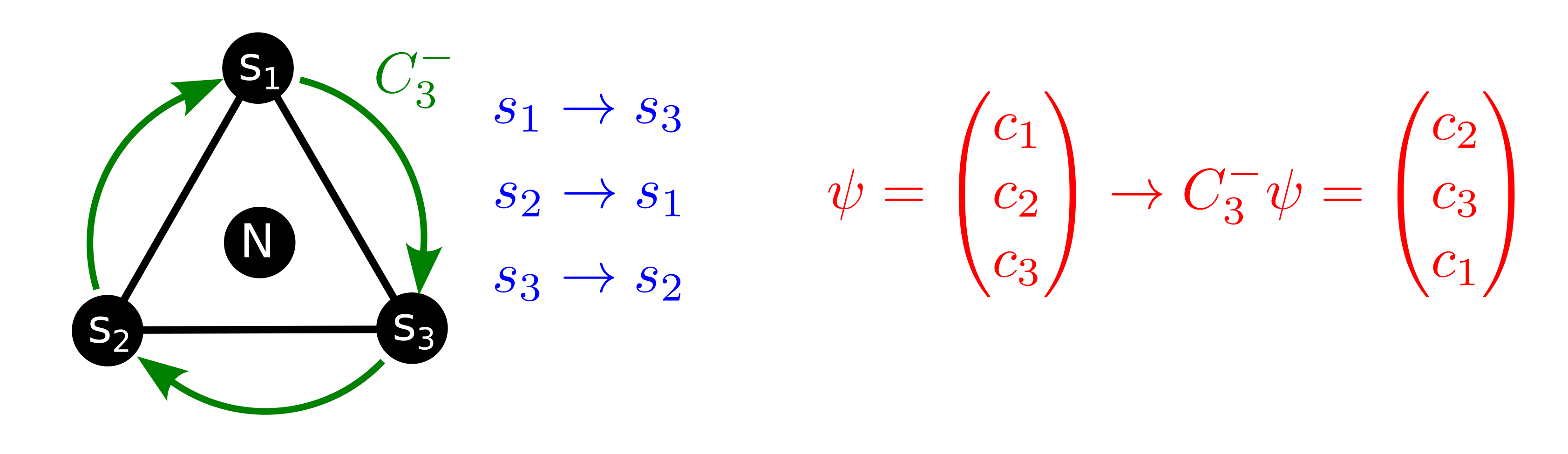
Fig. 124 Ejemplo del efecto de la operación \(C_3^-\) sobre la base de orbitales 1s del hidrógeno en el amoníaco y su representación con vectores.

Dado que al aplicar la operación \(C_3^-\) sobre la función \(s_1\), que representamos por el vector \((1,0,0)\) es la función \(s_3\), representada por el vector \((0,0,1)\), tenemos que:

(199)\[\begin{split}C_3^-\begin{pmatrix} 1 \\ 0 \\0 \end{pmatrix}=\begin{pmatrix} 0 \\ 0 \\1 \end{pmatrix}\end{split}\]

Si \(C_3^-\) es una matriz 3x3, la ecuación anterior define su primera fila.

(200)\[\begin{split}C_3^-=\begin{pmatrix} 0 & 0 & 1 \\c_{21} & c_{22} & c_{23} \\c_{31} & c_{32} &c_{33} \end{pmatrix}\end{split}\]

Si tomamos el efecto sobre \(s_2=(0,1,0)\) y \(s_3=(0,0,1)\) podemos encontrar que la matriz \(C_3^-\) en la representación de las funciones 1s del hidrógeno es,

(201)\[\begin{split}C_3^-=\begin{pmatrix} 0 & 0 & 1 \\1 & 0 & 0 \\0 & 1 &0 \end{pmatrix}\end{split}\]

Podemos operar de forma similar para obtener el efecto de la operación \(C_3^+\).

Fig. 125 Efecto de la operación \(C_3^+\) sobre la base de orbitales 1s del hidrógeno en el amoníaco y su representación vectorial.

y obtener la matriz,

(202)\[\begin{split}C_3^+=\begin{pmatrix} 0 & 1 & 0 \\0 & 0 & 1 \\1 & 0 &0 \end{pmatrix}\end{split}\]

Se puede comprobar que estas matrices cumplen todas las propiedades esperables de los operadores \(C_3^+\) y \(C_3^-\). Por ejemplo, podemos comprobar que \(C_3^+\) es la inversa de \(C_3^-\).

(203)\[\begin{split}C_3^+ C_3^- = I \rightarrow \begin{pmatrix} 0 & 0 & 1 \\ 1& 0& 0\\0&1&0\end{pmatrix} \begin{pmatrix} 0 & 1 & 0 \\ 0& 0& 1\\1&0&0\end{pmatrix} = \begin{pmatrix} 1 & 0 & 0 \\ 0& 1& 0\\0&0&1\end{pmatrix} \end{split}\]

Ejemplo: funciones N(2p) en el Amoníaco

Un ejemplo ligeramente más complejo es ver que le ocurre a las funciones 2p del átomo central (nitrógeno) en el amoníaco. La base es:

(204)\[\{N(p_x),N(p_y),N(p_z)\}\]

En las Fig. 126 y Fig. 127 representamos los orbitales \(N(p_x)\) y \(N(p_y)\) usando flechas rojas (la cabeza de la flecha apunta hacia el lóbulo positivo del orbital).

Cuando aplicamos una rotación de 120\(^o\) las flechas cambian de dirección lo que significa que los orbitales rotados pueden ser expresados por una combinación lineal de los orbitales originales (líneas continuas). Utilizando estas transformaciones podemos escribir las matrices en la base de los orbitales N(2p).

Fig. 126 Ilustración del efecto de la operación \(C_3^-\) sobre los orbitales 2p del nitrógeno (átomo central) en el amoníaco y cual es la representación de esta operación en esta base.

De forma similar podemos encontrar también la matriz de la operación \(C_3^+\),

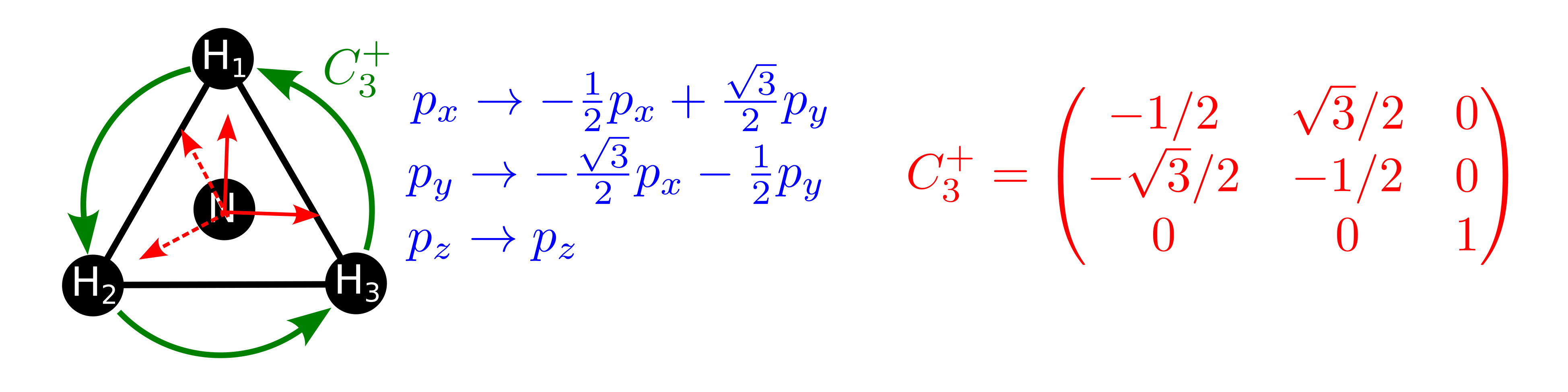
Fig. 127 Ilustración del efecto de la operación \(C_3^+\) sobre los orbitales 2p del nitrógeno (átomo central) en el amoníaco y cual es la representación de esta operación en esta base.

de la identidad,

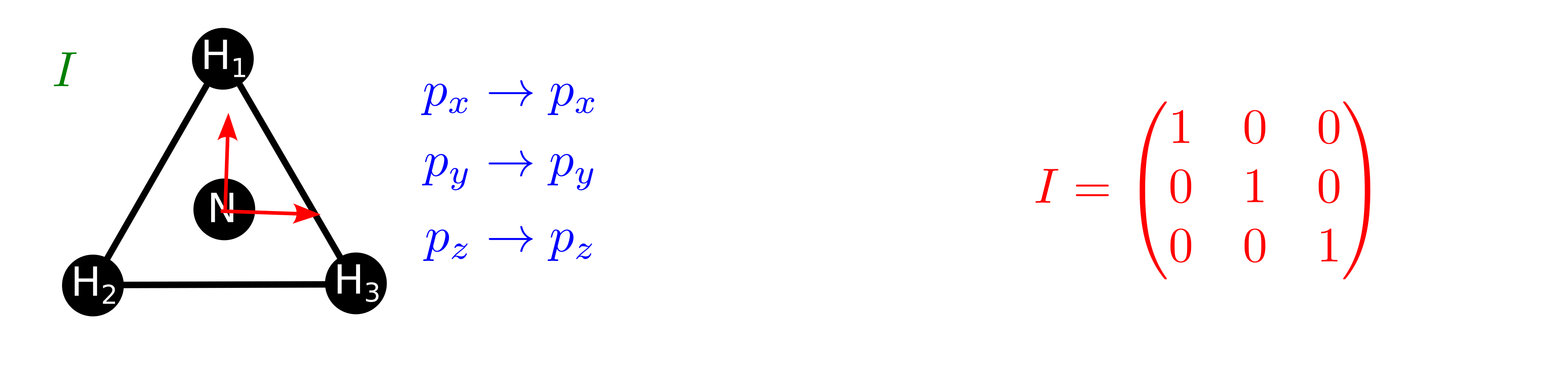
Fig. 128 Ilustración del efecto de la identidad \(I\) sobre los orbitales 2p del nitrógeno (átomo central) en el amoníaco y cual es la representación de esta operación en esta base.

o de los 3 planos de reflexión verticales,

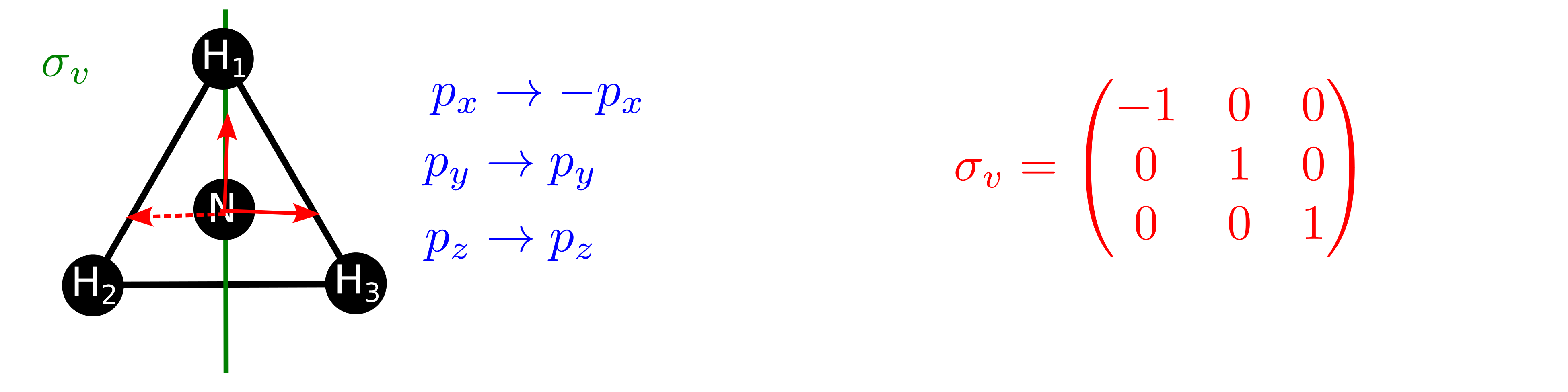
Fig. 129 Ilustración del efecto de la operación \(\sigma_v\) sobre los orbitales 2p del nitrógeno (átomo central) en el amoníaco y cual es la representación de esta operación en esta base.

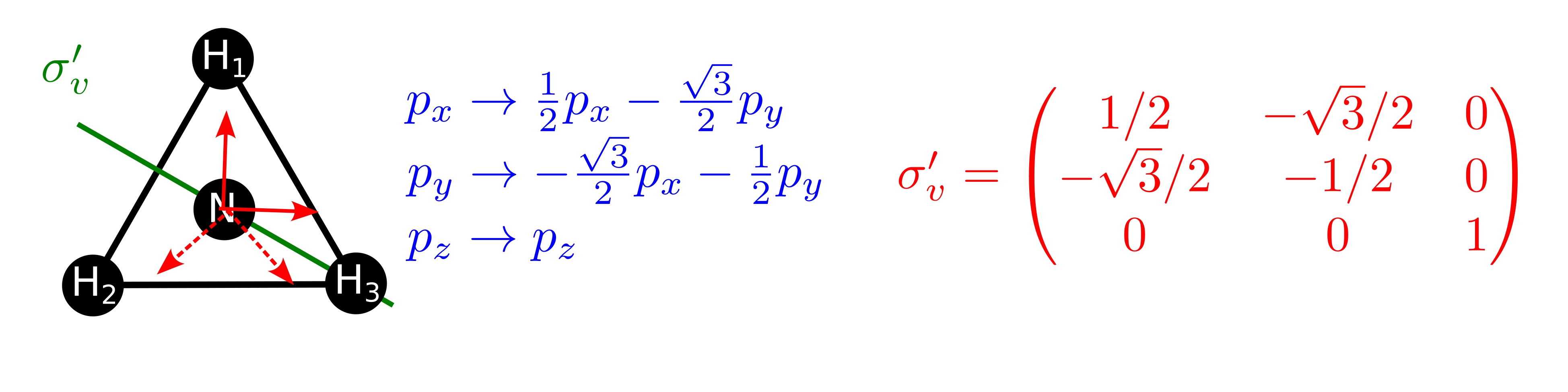
Fig. 130 Ilustración del efecto de la operación \(\sigma_v^\prime\) sobre los orbitales 2p del nitrógeno (átomo central) en el amoníaco y cual es la representación de esta operación en esta base.

Fig. 131 Ilustración del efecto de la operación \(\sigma_v^{\prime\prime}\) sobre los orbitales 2p del nitrógeno (átomo central) en el amoníaco y cual es la representación de esta operación en esta base.

Carácter de una operación

Llamamos carácter de una operación R en su representación D \(\chi(D(R))\), a la traza de la matriz que representa ese operador,

(205)\[\chi(D(R))=Tr(\vec{R})=\sum_a R_{aa}=\sum_a \left\langle\chi_a\right\vert \hat{R} \left\vert \chi_a \right\rangle\]

Los caracteres tienen las siguientes propiedades:

• El carácter de la identidad es igual a la dimensión de la base

• Las operaciones conjugadas tienen matrices diferentes pero el mismo carácter (ver las matrices más arriba y calcular el carácter de las operaciones conjugadas)

Efecto de la simetría en una función de onda

Cuando aplicamos una operación de simetría a un orbital molecular, que representamos mediante un vector, tenemos,

(206)\[\vert\psi^\prime\rangle = \hat{R}\vert\psi\rangle \rightarrow {c}^\prime_a = \sum_b R_{ab}c_b\]

si este orbital molecular es un autoestado del Hamiltoniano habíamos indicado que esperamos que este orbital sea un autovector del operador de simetría,

(207)\[\hat{R}\vert\psi_i\rangle = r_i \vert\psi_i\rangle \]

Interpretemos físicamente, ahora, este resultado. Supongamos que tenemos una molécula, con cierta forma, como la mostrada en la Fig. 132. Si aplicamos una operación de simetría sobre la molécula, dado que el resultado es físicamente indistinguible de la situación inicial, hará que todas las propiedades observables de la molécula no cambien.

Fig. 132 Ilustración de una molécula sencilla con simetría \(D_{4h}\) que, por ejemplo, puede ser rotada 90\(^o\) y quedar invariante.

Si consideramos, por ejemplo, la densidad electrónica, \(\rho(\vec{r})\), tenemos que, al aplicarle una operación de simetría,

(208)\[\hat{R}\rho(\vec{r})=\rho(\vec{r}) \]

la densidad no puede cambiar ya que el potencial de los núcleos que la generan es igual al inicial. Dado que la densidad es el módulo al cuadrado de la función de onda eso significa que, cuando aplicamos una operación de simetría la función de onda tan sólo cambia en una fase,

(209)\[\hat{R}\Psi(\vec{r},\vec{R})=e^{i\varphi}\Psi(\vec{r},\vec{R}^\prime)\]

Warning

El razonamiento que hemos seguido aquí no es del todo general y discutiremos el resultado exacto cuando se discutan las irreps

Es importante notar que los caracteres tienen mucho que ver con los elementos diagonales de la matriz y que la ecuación (209) está indicando que, precisamente, estos elementos diagonales son los autovalores de las operaciones de simetría.

Problemas y ejemplos

• Prueba que los tres planos de reflexión del NH\(_3\) son operaciones conjugadas utilizando las matrices de la representación N(2p) obtenidas en el ejemplo superior.