Molécula de amoníaco

Molécula de amoníaco#

Introducción#

Trabajemos ahora en la molécula de amoníaco (\(NH_3\)) que tiene una forma piramidal y está formada por átomo de nitrógeno y tres de hidrógeno (ver Fig. 180). Su estructura pertenece al grupo \(C_{3v}\) donde el eje principal pasa por el átomo de nitrógeno y el baricentro del triángulo equilátero que forman los átomos de hidrógeno.

../_images/ammonia.jpeg — Fig. 180 Ilustración de la superficie de amoníaco donde se presenta el nitrógeno como una esfera azul y los hidrógenos como esferas pequeñas blancas.#

La tabla de caracteres del grupo \(C_{3v}\) se presenta en la Fig. 181.

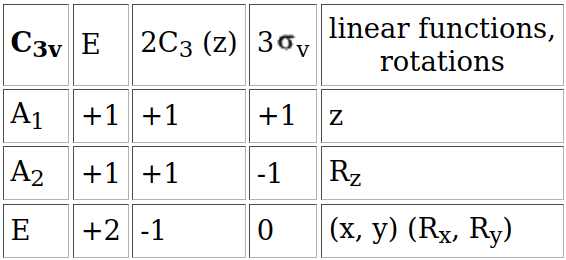
../_images/c3v_table.png — Fig. 181 Tabla de caracteres del grupo puntual \(C_{3v}\) al que pertenece la molécula de amoníaco en su mínimo de energía.#

Construcción de la base#

Seguidamente buscamos los orbitales de valencia de la molécula. Cada átomo de hidrógeno contribuye con un orbital 1s mientras que el átomo de nitrógeno tiene como orbitales de valencia el 2s y los 2p (\(p_x\), \(p_y\) y \(p_z\)). La descomposición de esta base en irreps se hizo en detalle en el tema de simetría. Veamos aquí como podemos simetrizarla de forma más rápida explotando todo lo posible la tabla de caracteres.

Simetrización#

Dado que el átomo de nitrógeno se encuentra en el centro de la molécula, usando la Tabla, Fig. 181, podemos identificar que:

El orbital 2s es totalmente simétrico (no cambia bajo ninguna operación de simetría) y, por tanto, pertenece a \(a_1\).
Tal y como se indica en la columna de la derecha el orbital \(2p_z\) pertenece, también, a \(a_1\).
Los orbitales \(2p_x\) y \(2p_y\) forman, conjuntamente, una irrep \(e\) doblemente degenerada.

Queda identificar cuales son las irreps a las que pertenecen los orbitales H(1s) del hidrógeno. Es claro que los orbitales del hidrógeno solapan con el orbital 2s del nitrógeno y con el \(2p_x\)/\(2p_y\) por lo que tienen que expandir una irrep \(a_1\) (solape con \(2s\)) y E (por el solape con \(2p_x\)/\(2p_y\)). Construir la irrep totalmente simétrica es lo más sencillo ya que debe ser un orbital que no cambie con las rotaciones, por lo que:

(308)#\[H_{a1}=\frac{1}{\sqrt{3}} \left(H_1(1s)+H_2(1s)+H_3(1s) \right) \]

Si ahora escogemos funciones que solapen máximamente con \(2p_x\) tenemos una función e,

(309)#\[H_{e,x}=\frac{1}{\sqrt{2}} \left(H_2(1s)-H_3(1s) \right) \]

y la función e que nos falta la podemos obtener del solape con \(2p_y\) haciendo que sea ortogonal a \(H_{a1}\) y \(H_{e,x}\),

(310)#\[H_{e,y}=\frac{1}{\sqrt{2}} \left(2H_1{1s}-H_2(1s)-H_3(1s) \right) \]

Hamiltoniano#

En la base inicial \(\{N(2s),N(2p_x),N(2p_y),N(2p_z),H_1(1s),H_2(1s),H_3(1s)\}\) y despreciando las interacciones entre los átomos de hidrógeno el Hamiltoniano es,

(311)#\[\begin{split}H= \begin{pmatrix} \varepsilon_{2s} & 0 & 0 & 0 & \gamma_{Hs} & \gamma_{Hs} & \gamma_{Hs}\\ 0 & \varepsilon_{2p} & 0 & 0 & 0 & \gamma_{Hxy} & -\gamma_{Hxy}\\ 0 & 0 & \varepsilon_{2p} & 0 & \sqrt{2}\gamma_{Hxy} & -\gamma_{Hxy} & -\gamma_{Hxy}\\ 0 & 0 & 0 & \varepsilon_{2p} & -\gamma_{Hz} & -\gamma_{Hz} & -\gamma_{Hz}\\ \gamma_{Hs} & 0 & \sqrt{2}\gamma_{Hxy} & -\gamma_{Hz} &\varepsilon_{H} & 0 & 0\\ \gamma_{Hs} & \gamma_{Hxy} & -\gamma_{Hxy} & -\gamma_{Hz} & 0 & \varepsilon_{H} & 0\\ \gamma_{Hs} &-\gamma_{Hxy} & -\gamma_{Hxy} & -\gamma_{Hz} & 0 & 0 & \varepsilon_{H}\\ \end{pmatrix} \end{split}\]

mientras que en la base simetrizada \(\{N(2s),N(2p_z),H_{a_1},N(2p_x),N(2p_y),H_{e,x},H_{e,y}\}\)

(312)#\[\begin{split}H= \begin{pmatrix} \varepsilon_{2s} & \sqrt{3}\gamma_{Hs} & -\sqrt{3}\gamma_{Hz} & 0 & 0 & 0 & 0\\ \sqrt{3}\gamma_{Hs} & \varepsilon_{2p} & 0 & 0 & 0 & 0 & 0\\ -\sqrt{3}\gamma_{Hz} & 0 & \varepsilon_{2p} & 0 & 0 & 0 & 0\\ 0 & 0 & 0 & \varepsilon_{2p} & 0 & \sqrt{2}\gamma_{Hxy} & 0\\ 0 & 0 & 0 & 0 &\varepsilon_{2p} & 0 & \sqrt{2}\gamma_{Hxy}\\ 0 & 0 & 0 & \sqrt{2}\gamma_{Hxy} & 0 & \varepsilon_{H} & 0\\ 0 &0 & 0 & 0 & \sqrt{2}\gamma_{Hxy} & 0 & \varepsilon_{H}\\ \end{pmatrix} \end{split}\]

Es claro que de los 3 orbitales \(a_1\) va a haber uno muy enlazante con carácter 2s mezclado, parcialmente con 2p\(_z\) y orbitales 1s del hidrógeno, otro poco enlazante, principalmente \(2p_z\) con hidrógeno y otro muy antienlazante de los hidrógenos, principalmente. Por otro lado los orbitales \(p_x,p_y\) forman una irrep e que interacciona con los E de los hidrógenos dando lugar a un orbital E enlazante (principalmente del 2p del nitrógeno) y otro antienlazante (principalmente de los 2p de los hidrógenos). El resultado se muestra en la Fig. 182.

../_images/nh3_molorb.png — Fig. 182 Orbitales moleculares del amoníaco.#

Otros problemas moleculares se realizan de forma similar.