Hamiltoniano nuclear

En la introducción describimos un método para la resolución del Hamiltoniano molecular total, incluyendo núcleos y electrones, donde se debían resolver 2 ecuaciones. Una aportaba el movimiento electrónico,

(316)\[\hat{H}_e(\{\vec{r}\},\{\vec{R}\})\Psi_e^{(i)} = E_i(\{\vec{R}\}) \Psi_e^{(i)}\]

y la otra el nuclear,

(317)\[\left(\hat{T}_n + E_i(\{\vec{R}\})\right)\Psi_n^{\alpha}=E_{i,\alpha}\Psi_n^{\alpha}.\]

Este último problema, la dinámica nuclear, tiene que ver con el cálculo de la función de onda nuclear en la superficie electrónica del estado \(\alpha\), \(\Psi_n^{\alpha}\), tal y como se ilustra en la Fig. 207. Esta sección estará dedicada al análisis de los diferentes grados de libertad y escalas de energía que caracterizan diferentes fenómenos típicos de la solución de la Ec. (317).

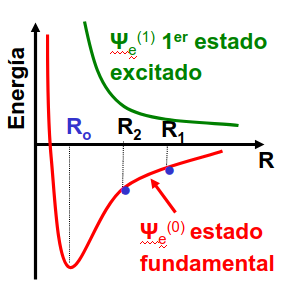
Fig. 207 Ejemplo de superficies de energía, autovalores de la ecuación (316), y que sirven de potencial para el movimiento nuclear, Ec. (317). En este caso podemos imaginarnos que R es una distancia interatómica en una molécula diatómica y las 2 superficies se corresponden con 2 estados electrónicos diferentes.

Grados de libertad nucleares en una molécula

Cuando imaginamos una molécula en fase gas, normalmente se encontrará cerca del mínimo absoluto de la energía del estado fundamental, \(E_i\). Esto da a la molécula una cierta forma que viene dada por la geometría del punto de equilibrio, \(\vec{R}_{\text{eq}}\). A partir de este punto podemos analizar los diferentes tipos de movimiento de los núcleos que pueden ocurrir, sobre todo si asumimos que la geometría no se alejará mucho de \(\vec{R}_{\text{eq}}\).

Si la molécula contiene N átomos, habrá 3N grados de libertad asociados a la molécula, dado que cada átomo se puede mover a lo largo de 3 ejes (x, y, z). Primero consideraremos movimientos que no deforman la molécula, es decir, que mantienen las posiciones relativas de los átomos fijas y que, por tanto, no alterarán la energía \(E_i\). Estas son:

• Traslaciones: Si desplazamos a la molécula rígidamente en la geometría \(\vec{R}_{\text{eq}}\) (ver Fig. 208), es decir, producimos una traslación, su energía electrónica, \(E_i\), no cambiará, aunque, dependiendo a que velocidad se desplace su centro de masa, la energía cinética de la molécula en conjunto cambiará de forma continua.

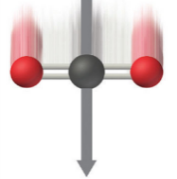
Fig. 208 Se ilustra una molécula de CO\(_2\) en su geometría de equilibrio, \(D_{\infty h}\), desplazándose rígidamente a lo largo de su vector velocidad, mostrado como una flecha gris. Cuanto mayor sea su velocidad, mayor energía cinética tendrá la molécula.

• Rotaciones: Por otro lado si rotamos la molécula rígidamente (ver Fig. 209), manteniendo la geometría \(\vec{R}_{\text{eq}}\), su energía electrónica, \(E_i\), tampoco cambiará. Este movimiento, equivalente a la rotación de un sólido rígido en mecánica clásica, en mecánica cuántica viene caracterizado por el rotor cuántico (ver rotaciones). El parámetro principal para obtener los niveles rotacionales es el tensor de inercia, que viene descrito por la geometría del estado fundamental, \(\vec{R}_{\text{eq}}\), y las masas de los núcleos de la molécula. En las moléculas no lineales hay 3 grados de libertad rotaciones correspondientes a la rotación alrededor de los ejes x, y y z. En las moléculas lineales la rotación alrededor del eje principal de la molécula (eje z) no cambia la geometría y, por tanto, sólo hay 2 grados de libertad rotacionales.

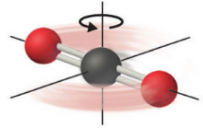
Fig. 209 Se ilustra una molécula de CO\(_2\) en su geometría de equilibrio, \(D_{\infty h}\), rotando a lo largo de un eje (x o y) perpendicular a su eje principal (ejez). Cuanto mayor momento angular tenga la molécula, más rápido girará la misma (\(J=I\omega\)) y más energía cinética tendrá.

• Vibraciones: Finalmente, podemos deformar la molécula alrededor de la posición de equilibrio (ver Fig. 210). Si este movimiento es lo suficientemente pequeño podemos considerar que la superficie de energía \(E_i\) alrededor de la geometría de equilibrio \(\vec{R}_{\text{eq}}\) es aproximadamente cuadrática. Esto dará lugar a 3N-6 (3N-5 en moléculas lineales) grados de libertad vibracionales que vendrán caracterizados por un oscilador cuántico, como se describe en la sección vibraciones).

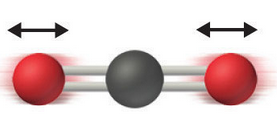
Fig. 210 Se ilustra una molécula de CO\(_2\) donde los átomos de oxígeno se mueven de forma simétrica acercándose y alejándose del átomo de carbono central. Este movimiento cambia \(E_i\) y puede resultar en diferentes frecuencias de vibración dependiendo de la forma en que se deforme la molécula (modo de vibración).

Niveles de energía y sus escalas

Los tipos de niveles descritos anteriormente no sólo tienen una entidad formal, asociada al movimiento rígido o deformación de la geometría de la molécula, si no que, además, tienen asociada una escala de energía caracterísitica dada en la Tabla escala de energía, Fig. 211. En particular, las traslaciones ocurren en un contínuo de energía y la separación de energía entre estos niveles es, esencialmente, cero. Por otro lado los niveles rotaciones tienen separaciones de 1-100 cm\(^{-1}\) y se pueden observar en la parte de microndas del espectro electromagnético. Por su parte, los niveles vibracionales tienen energías características de decimas de electronvoltio (centenares de cm\(^{-1}\)) y se observan en el infrarrojo (IR). Finalmente, las transiciones electrónicas entre niveles de valencia tienen energías típicas de algunos electronvoltios (decenas de miles de cm\(^{-1}\)) y se observan en el visible y el ultravioleta.

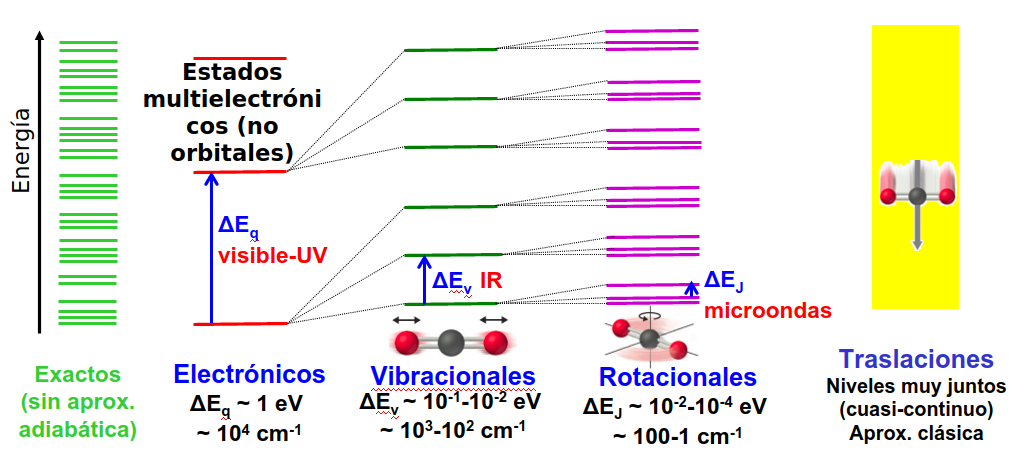
Fig. 211 Ilustración de las diferentes escalas energéticas a las que, normalmente, ocurren transiciones de niveles en una molécula. Como puede verse cada nivel electrónico tiene, a su vez, niveles vibracionales asociados y estos, a su vez, rotacionales, lo que produce una compleja estructura y hace qeu la observación experimental de los espectros sea una forma de obtener información muy detallada de las moléculas.

Por tanto, es muy importante conocer estas escalas para poder interpretar los datos experimentales disponibles para las moléculas y conocer sus propiedades.

Cambio de coordenadas

Para poder extraer los tipos de movimiento anteriores hay que hacer un cambio de coordenadas en las que expresamos el Hamiltoniano dado por Ec. (317). Hasta ahora hemos utilizado coordenadas cartesianas de cada átomo, \(\vec{R}_\alpha\), y deseamos pasar a coordenadas colectivas que involucran a todos los átomos de la molécula y que denotaremos por \(Q_\alpha\).

Las más sencillas de definir son las de las traslaciones, ya que tan sólo involucran el cálculo de las coordenadas del centro de masa de la molécula (que define su movimiento rígido),

(318)\[\vec{Q}_{\text{CM}}= \frac{\sum_\alpha M_\alpha \vec{R}_\alpha}{\sum_\alpha M_\alpha} \]

Las coordenadas asociadas a la rotación son los ángulos de Euler que permiten definir el giro de la molécula alrededor de 3 ejes independientes. Finalmente los movimientos vibracionales se expresarán en modos que serán combinaciones lineales de los desplazamientos atómicos del átomo \(\alpha\) en la dirección x, \(R_{\alpha,x}\),

(319)\[Q_{\gamma}= \sum_\alpha c_{\gamma,\alpha x} R_{\alpha,x} \]

Problems and solution examples