Grupos puntuales#
La definición de las operaciones de simetría nos permite ver que ocurre cuando las aplicamos una tras otra y como, cuando las consideramos todas juntas, adquieren una estructura matemática que, inicialmente, nos va a permitir clasificar las moléculas según su forma y, posteriormente, nos va a permitir simplificar la resolución de la ecuación de Schrödinger. Esta estructura matemática es el grupo y vamos a utilizar sus propiedades durante la mayor parte del curso.
¿Qué es un grupo?#
Para definir un grupo necesitamos:
(1) Un conjunto de elementos, que para nosotros va a tratarse de todas las operaciones de simetría asociadas a una geometría particular de una molécula y
(2) una operación, la multiplicación, entre dos elementos del grupo. Para nosotros va a tratarse de lo que le ocurre a la molécula cuando primero aplicamos una operación de simetría y luego aplicamos la segunda sobre el resultado de la primera operación.
Ejemplo
Supongamos que tenemos las operaciones inversión (\(i\)) y plano de reflexión perpedicular al eje x (\(\sigma_v^x\)) (ver Fig. 26).
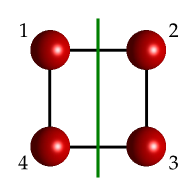
Fig. 26 Molécula cuadrada sencilla mostrando la numeración inicial de los átomos y un plano vertical. El centro de inversión estaría en el centro del cuadrado.#
Individualmente cada operación (\(i\), \(\sigma_v^x\)) produce los siguientes cambios:
El producto \(\sigma_v\times i\) (aplicamos primero la inversión y luego el plano) tiene el siguiente efecto:
Podemos observar que el resultado de multiplicar \(i\) por \(\sigma_v^x\) es un plano de reflexión equivalente a \(\sigma_v^x\) pero a lo largo del eje y (\(\sigma_v^y\)), es decir, otra de las operaciones de simetría del sistema.
Para que el conjunto de las operaciones de simetría y su multiplicación formen un grupo deben darse las siguientes condiciones:
Cerrado: La multiplicación de cualquier elemento del grupo por otro debe dar un elemento del conjunto inicial. Es decir, que el producto de dos operaciones de simetría debe dar otra operación de simetría. Dado que todas las operaciones de simetría mantienen la geometría de la molécula esta propiedad debe verificarse una vez que hemos encontrado todas las operaciones de simetría de un sistema.
Propiedad asociativa: Dadas tres operaciones \(A\), \(B\) y \(C\) se cumple que:
Elemento neutro: Dentro del grupo existe un elemento \(I\) tal que:
En nuestro caso podemos pensar siempre que una rotación de orden 1 (que rota \(2\pi/1=2\pi\), una vuelta completa) es el elemento neutro ya que al núcleo \(i\) le asigna siempre el núcleo \(i\). A esta operación la denotaremos con la letra \(E\).
Elemento inverso: Dentro del grupo debe existir siempre un elemento \(A^{-1}\) tal que:
Es sencillo ver que un plano de reflexión es siempre su propio inverso, o que una rotación negativa es el inverso de una positiva y viceversa.
El grupo de las operaciones puntuales de una molécula#
Para encontrar el grupo de una molécula lo que haremos será buscar todas las operaciones de simetría, tal y como se definieron anteriormente. Estas operaciones de simetría, a diferencia de las de los sólidos mantienen, siempre, al menos un punto del espacio fijo. Es por ello que se denominan operaciones puntuales de simetría y el grupo que obtengamos será un grupo puntual.
Para formar el grupo puntual de la molécula es necesario encontrar todas las operaciones de simetría. Por ejemplo, un eje de orden n (ver Fig. 27) no contiene una sola operación de rotación si no que contiene n de estas operaciones, cada una girando un ángulo \(2\pi i/n\) donde \(i=0,...,n-1\).
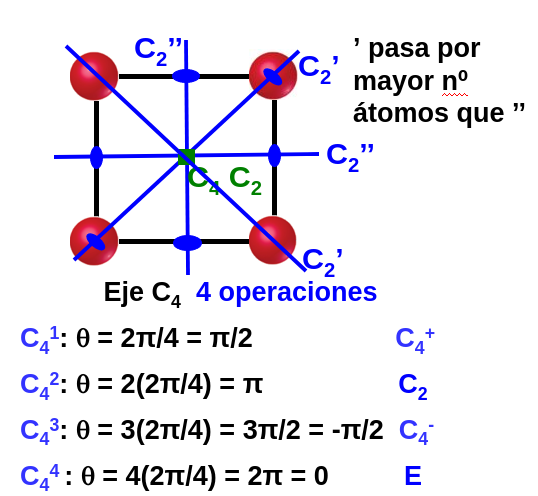
Fig. 27 Ilustración de las operaciones asociadas a un eje de rotación en una molécula cuadrada. Se muestran además varios de los planos de reflexión presentes en la molécula.#
Es fácil darse cuenta que este conjunto completo de operaciones verifica las condiciones para formar un grupo descritas arriba. Una manera interesante de escribir las operaciones del grupo (que tiene que ver con aplicaciones más avanzadas de la simetría que las que trataremos en este curso) es numerar los núcleos, como hemos hecho hasta ahora, y escribir todas las permutaciones posibles cambiando de posición núcleos equivalentes [2].
La notación más usual para los grupos puntuales en moléculas es la de Schönflies que suele constar de una letra mayúscula y un subíndice, \(X_y\). Aquí no entraremos en muchos detalles, bastará decir que la letra mayúscula viene asociada a la forma principal de la molécula donde, por ejemplo, los grupos con una \(O\) serán octaédricos, con una \(T\) tetraédricos, etc. mientras que el subíndice aporta información sobre algunas operaciones de simetría importantes como el eje de rotación de mayor orden o la presencia de un plano de reflexión horizontal. Puedes encontrar detalles sobre la notación aquí.
Clasificación de moléculas según su grupo puntual de simetría#
Aquí vamos a responder a la pregunta práctica de como encontramos el símbolo del grupo, lo que nos ayudará a consultar tablas de simetría más adelante, una vez conozcamos las operaciones de simetría de la molécula. La respuesta la encontramos siguiendo el diagrama de la Fig. 28 desde la parte superior y respondiendo a cada una de las preguntas que nos vamos encontrando. Obtendremos el símbolo del grupo una vez se haya llegado a un círculo (en algunos casos tendremos que substituir la n en el subíndice por el orden de la rotación más alto presente en la molécula).
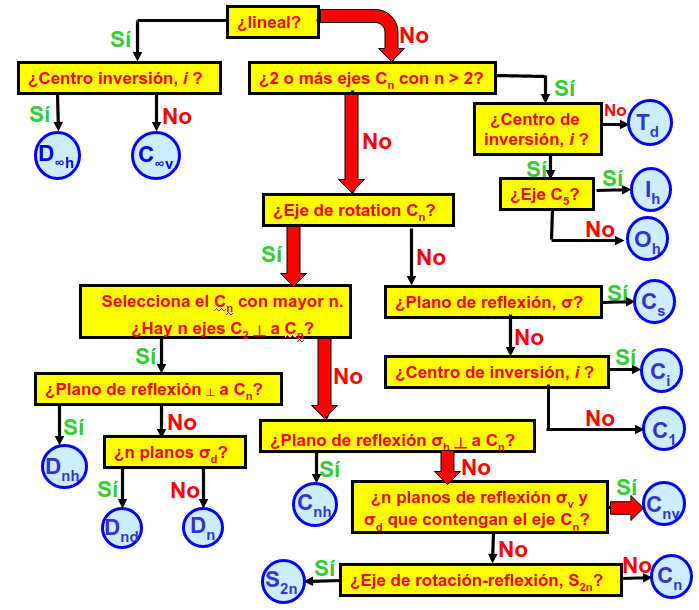
Fig. 28 Tabla de flujo utilizada para encontrar el grupo puntual de una molécula si se conocen todas las operaciones de simetría que contiene. Se debe empezar en la parte superior (¿lineal?) e ir respondiendo SI o NO a cada una de las preguntas hasta llegar a un círculo que indicará el grupo.#
Propiedades de las moléculas según su grupo#
En 1935 John von Neumann enunció su principio de relación simetría-propiedades. Lo que dice es lo siguiente:
Las propiedades macroscópicas de un sistema deben tener, al menos, la simetría del grupo puntual del sistema
Lo que quiere decir esto es que si un sistema es cuadrado, cuando midamos sus propiedades deben ser consistentes con esa forma, de modo que nunca podremos observar una simetría más baja (como la de un rectángulo) pero quizá si una más alta (como la de una esfera). Esto es relativamente sencillo de visualizar, si nos imaginamos un gas de molécula cuadradas y hacemos una medida en un tiempo macroscópico. Lo que probablemente ocurrirá es que, como las moléculas están girando en el espacio, observemos un promedio de todas las orientaciones que toman las moléculas que, en fase gas, sería algo isótropo (una esfera) en vez de algo cuadrado. En cualquier caso ninguna forma de promediado va a hacer que veamos una molécula cuadrada como una rectangular.
Además el grupo puntual impone restricciones importantes a que sistemas pueden poseer algunas propiedades importantes. Más abajo nos centramos en la polaridad de una molécula y la quiralidad, aunque reglas similares pueden encontrarse para otras propiedades.
Moléculas polares#
Si consideramos que el átomo \(\alpha\) dentro de una molécula tiene carga \(\vec{q}_\alpha\) el momento dipolar eléctrico de la misma se define,
Las moléculas polares poseen un momento dipolar eléctrico no nulo y las apolares nulo. Puede comprobarse que para que una molécula sea polar deben de darse las condiciones:
No puede haber centro de inversión (\(i\))
Sólo puede haber un eje de rotación \(C_n\) que estará en la dirección de \(\mu\).
No puede haber planos perpendiculares a \(C_n\)
Con estas restricciones los únicos grupos puntuales con las moléculas polares son \(C_s\), \(C_n\) y \(C_{nv}\). Ver algunos ejemplos en la Fig. 29.
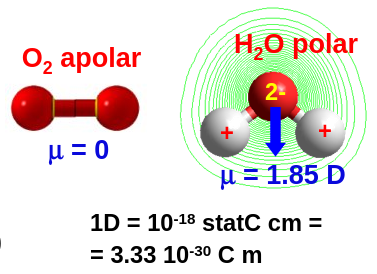
Fig. 29 La molécula de oxígeno pertenece al grupo \(D_{\infty h}\) por lo que no es polar al tener un plano \(\sigma_h\) perpendicular a su superficie de rotación \(C_{\infty}\). La molécula de agua es \(C_{2v}\) por lo que es polar.#
Moléculas quirales#
Las moléculas quirales no se pueden superponer con su imagen especular. Esto hace que, evidentemente, no puedan contener ningún plano de reflexión pero, además, no pueden contener ningún eje impropio de rotación por lo que los únicos grupos quirales son \(C_n\) y \(D_n\).
