Ejemplos

Dada la importancia de la red recíproca, en esta sección vamos a calcular, de forma detallada, varios ejemplos de su obtención, cuando el sistema es periódico en 1D, 2D o 3D.

Red recíproca en 1 dimensión

Supongamos una red directa con un parámetro de red (periodo) \(a\), tal y como se muestra en la Fig. 65.

Fig. 65 Ilustración de red directa en 1 dimensión con parámetro de malla \(a\). Los puntos se denotan \(\vec{R}_{n-1}\), \(\vec{R}_n\), \(\vec{R}_{n+1}\),…

Se puede utilizar ahora la definición de la red recíproca basada en el producto de vectores de la red directa con la recíproca tenemos,

(67)\[\vec{G}\cdot \vec{R}_n = 2\pi N, N\in\mathbb{Z}\]

Aunque el sistema sea en 1 dimensión podemos utilizar las expresiones usuales en varias dimensiones, imaginándonos que el parámetro de malla en las direcciones no periódicas es infinito. Sabemos que el vector \(\vec{a}^*\) va a ser perpendicular a \(\vec{a}_2\) que se encuentra en la dirección \(\vec{u}_y\) y a \(\vec{a}_3\) que se encuentra en la dirección \(\vec{u}_z\),

(68)\[\vec{a}_1^\star \cdot\vec{a}_2 = \frac{2\pi}{V}\left(\vec{a}_2\times\vec{a}_3\right)\cdot\vec{a}_2 = 0\]

Por tanto, el vector \(\vec{a}_1^\star\) debe venir en la dirección \(\vec{u}_x\) y, usando la Ec. (67) podemos determinar su módulo,

(69)\[\vec{G}_m = \frac{2\pi}{a} m \vec{u}_x \rightarrow \vec{a}^*=\frac{2\pi}{a} \vec{u}_x \]

Por tanto, podemos ver que la red recíproca de una red directa unidimensional es otra red unidimensional de parámetro de malla \(2\pi/a\).

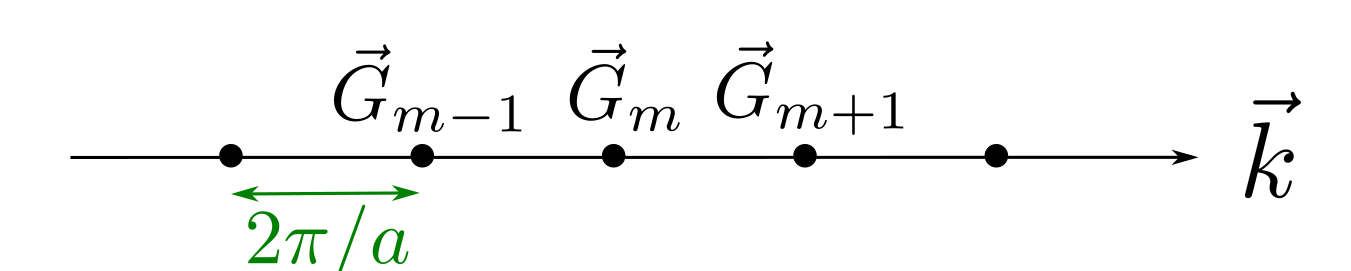
Fig. 66 Ilustración de la red recíproca asociada a la red directa unidimensional ilustrada en la Fig. 65. Puede observarse que el parámetro de malla es \(2\pi/a\).

Red recíproca en 2 dimensiones

Fig. 67 Ilustración de una red oblicua en 2 dimensiones de parámetros de malla \(a_1\) y \(a_2\) y \(\alpha\) (ángulo entre los vectores).

Para calcular un ejemplo de red recíproca en 2 dimensiones vamos a partir de una red directa oblicua (ver Fig. 67). Como en el caso anterior vamos a suponer que tenemos 3 vectores de red pero haremos que el parámetro de malla asociado a la dirección no periódica (c) sea muy grande (lo haremos tender a infinito).

(70)\[\vec{a}_1 = a \vec{u}_x ~~~~~ \vec{a}_2 = b (\cos\alpha\vec{u}_x + \sin\alpha \vec{u}_y) ~~~~~~ \vec{a}_3 = c\vec{u}_z\]

Los dos primeros vectores de la red recíproca, mediante su definición, son,

(71)\[ \vec{a}_1^\star = \frac{2\pi}{V} \vec{a}_2 \times \vec{a}_3 = \frac{2\pi}{ab\sin\alpha} b(\sin\alpha \vec{u}_x - \cos\alpha \vec{u}_y) = \frac{2\pi}{a}(\vec{u}_x-\frac{\cos\alpha}{\sin\alpha}\vec{u}_y)\]

(72)\[ \vec{a}_2^\star = \frac{2\pi}{V} \vec{a}_2 \times \vec{a}_3 = \frac{2\pi}{ab\sin\alpha} a\vec{u}_y = \frac{2\pi}{b} \frac{1}{\sin\alpha} \vec{u}_y\]

Al calcular el tercer vector podemos ver que depende en el denominador de c,

(73)\[ \vec{a}_3^\star = \frac{2\pi}{V} \vec{a}_1 \times \vec{a}_2 = \frac{2\pi}{c}\vec{u}_z\]

Dado que \(c\) es muy grande, el módulo de este vector tiende a cero y la red recíproca es periódica tan sólo en 2 dimensiones asociadas a los vectores \(\vec{a}_1^\star\) y \(\vec{a}_2^\star\). Cuando analizamos la solución de forma gráfica (Fig. 68) podemos observar que el vector \(\vec{a}_1^\star\) es perpendicular a \(\vec{a}_2\) y que \(\vec{a}_2^\star\) lo es, a su vez, de \(\vec{a}_1\). La red recíproca, por tanto, es una red bidimensional oblicua que está rotada \(90-\alpha\) grados respecto a la directa.

Fig. 68 Ilustración de la red recíproca bidimensional de la red oblícua 2D mostrada en la Fig. 67. Los vectores de la red directa, en rojo, se han superpuesto con las de la recíproca (en azul) para poder observar el angulo entre ellas. Notar que no tienen una escala común ya que los vectores de la red directa se miden en Å y lo de la recíproca en Å\(^{-1}\).

Red recíproca en 3 dimensiones

Seguidamente estudiaremos las redes recíprocas de las redes directas cúbicas.

Cúbica P

Los vectores de la red directa cúbica P son los siguientes,

(74)\[ \vec{a}_1 = a \vec{u}_x ~~~~~ \vec{a}_2 = a \vec{u}_y ~~~~~~ \vec{a}_3 = a\vec{u}_z \]

Fig. 69 Ilustración de una red directa cúbica P junto con sus vectores primitivos \(\vec{a}_1\), \(\vec{a}_2\) y \(\vec{a}_3\).

Calculamos ahora el volumen de la celda primitiva,

(75)\[\begin{split} V=\vec{a}_1 (\vec{a}_2\times \vec{a}_3 ) = a\vec{u}_x \begin{vmatrix} \vec{u}_x & \vec{u}_y & \vec{u}_z \\ 0 & a & 0 \\ 0 & 0 & a \end{vmatrix}=a\vec{u}_x a^2 \vec{u}_x = a^3\end{split}\]

Utilizamos la definición para calcular los vectores de base de la red recíproca primitiva,

(76)\[\begin{split} \vec{a}_1^\star = \frac{2\pi}{V} \vec{a}_2\times \vec{a}_3 = \frac{2\pi}{V} \begin{vmatrix} \vec{u}_x & \vec{u}_y & \vec{u}_z \\ 0 & a & 0 \\ 0 & 0 & a \end{vmatrix}=\frac{2\pi}{a^3}a^2\vec{u}_x = \frac{2\pi}{a}\vec{u}_x\end{split}\]

(77)\[ \vec{a}_2^\star =\frac{2\pi}{a}\vec{u}_y\]

(78)\[ \vec{a}_3^\star =\frac{2\pi}{a}\vec{u}_z \]

De este modo podemos observar que la red recíproca de una red cúbica P es, a su vez, una red cúbica P de parámetro \(2\pi/a\).

Fig. 70 Ilustración de la red recíproca de una red cúbica P. Podemos observar que también se trata de una red cúbica P.

Cúbica I

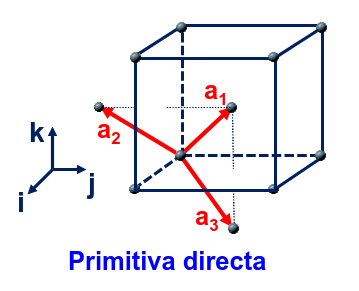
Fig. 71 Ilustración de una red directa cúbica I con sus vectores de red primitivos \(\vec{a}_1\), \(\vec{a}_2\) y \(\vec{a}_3\) en rojo.

Tomando como definición de los vectores de la red cúbica I lo que mostramos en la Fig. 71 podemos escribirlos algebraicamente tal y como los mostramos en la Ec. (79) y podemos encontrar la base primitiva de la red recíproca tal y como hemos hecho más arriba,

(79)\[\vec{a}_1 = \frac{a}{2} \left(\vec{u}_x + \vec{u}_y +\vec{u}_z\right) \leftrightarrow a_1^\star = \frac{2\pi}{a} \left(\vec{u}_y +\vec{u}_z\right) = \frac{4\pi}{a} \frac{1}{2}\left(\vec{u}_y +\vec{u}_z\right)\]

(80)\[\vec{a}_2 = \frac{a}{2} \left(\vec{u}_x - \vec{u}_y +\vec{u}_z\right) \leftrightarrow a_2^\star = \frac{2\pi}{a} \left(\vec{u}_x -\vec{u}_y\right) = \frac{4\pi}{a} \frac{1}{2}\left(\vec{u}_x -\vec{u}_y\right)\]

(81)\[\vec{a}_3 = \frac{a}{2} \left(\vec{u}_x + \vec{u}_y -\vec{u}_z\right) \leftrightarrow a_3^\star = \frac{2\pi}{a} \left(\vec{u}_x -\vec{u}_z\right) = \frac{4\pi}{a} \frac{1}{2}\left(\vec{u}_x -\vec{u}_z\right)\]

Representando los vectores de la red recíproca (ver Fig. 72) podemos observar que el resultado es una red de tipo F que también es cúbica y tiene un parámetro de malla \(4\pi/a\).

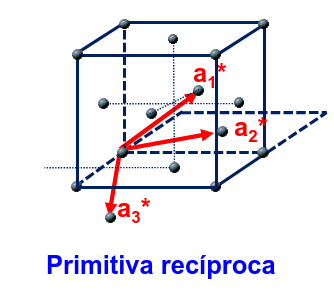
Fig. 72 Red recíproca cúbica en 3d

Cúbica F

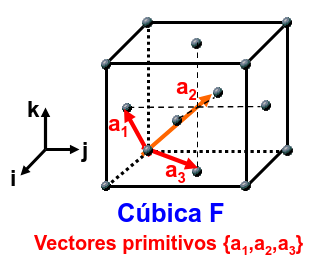
Fig. 73 Red directa cúbica F en 3d

Tomando como definición de los vectores de la red cúbica F, que se muestran en la Fig. 73, podemos escribirlos algebraicamente (Ec. (82)) y encontrar la base primitiva de la red recíproca tal y como hemos hecho más arriba,

(82)\[\vec{a}_1 = \frac{a}{2} \left(\vec{u}_y +\vec{u}_z\right) \leftrightarrow a_1^\star = \frac{4\pi}{a} \frac{1}{2}\left(\vec{u}_x + \vec{u}_y +\vec{u}_z\right)\]

(83)\[\vec{a}_2 = \frac{a}{2} \left(\vec{u}_x -\vec{u}_y\right) \leftrightarrow a_2^\star = \frac{4\pi}{a} \frac{1}{2}\left(\vec{u}_x - \vec{u}_y +\vec{u}_z\right)\]

(84)\[\vec{a}_3 = \frac{a}{2} \left(\vec{u}_x -\vec{u}_z\right) \leftrightarrow a_2^\star = \frac{4\pi}{a} \frac{1}{2}\left(\vec{u}_x + \vec{u}_y -\vec{u}_z\right)\]

Representando los vectores de la red recíproca (ver Fig. 74) podemos observar que el resultado es una red de tipo I que también es cúbica y tiene un parámetro de malla \(4\pi/a\).

Fig. 74 Ilustración de la red recíproca de una red directa cúbica F. Se puede apreciar que el resultado es una red cúbica I.

Es decir, cuando calculamos la red recíproca de una celda cúbica siempre encontramos otra celda cúbica. En particular la red recíproca de una red cúbica P es otra red cúbica P de parámetro \(2\pi/a\). En cambio cuando calculamos la red recíproca de una red cúbica I de parámetro \(a\) encontramos una red recíproca F de parámetro \(4\pi/a\) y cuando partimos de una red cúbica F de parámetro \(a\) encontramos una red I de parámetro \(4\pi/a\). Es decir, el sistema cristalino se mantiene constante ene la transformación pero no así la red de Bravais. Esto no es algo particular de las redes cúbicas si no algo general para todos los sistemas cristalinos.

Problemas y ejemplos