Hartree-Fock

Tal y como hemos indicado en el apartado anterior, nuestro objetivo es resolver el problema electrónico dado por la Ec. (115). Este problema de autovalores es muy difícil de resolver ya que, si tenemos \(N_e\) electrones, la función de onda tiene 3\(N_e\) dimensiones y no vamos a poder encontrar ninguna solución analítica a la misma.

Es, por tanto, necesario recurrir a aproximaciones para poder resolver la ecuación de Schrödinger asociada al Hamiltoniano electrónico. En mecánica cuántica hay dos métodos básicos para realizar aproximaciones (se recomienda leer los capítulos correspondientes en la Ref. [4]):

• En los métodos perturbativos se debe conocer la solución a un problema con una Hamiltoniano que describe la parte principal del problema y la aproximación permite encontrar correcciones asociadas a un Hamiltoniano más completo que no difiere mucho del inicial (Hamiltoniano perturbado).

• En los métodos variacionales se desconoce la solución a alguna parte del problema por lo que se propone una función de onda aproximada para el estado fundamental que depende de parámetros. El teorema variacional lo que nos indica es que, cuando se escoja esta función de onda, siempre tendrá una energía mayor a la del estado fundamental. Si variamos los parámetros para minimizar la energía nos podremos ir acercando a la energía del estado fundamental, que podremos alcanzar tan sólo si damos con la solución exacta.

Una vez introducido el problema veamos, exactamente, en qué consiste la aproximación de Hartree-Fock. Este apartado es, quizá, el que contiene más desarrollo matemático del curso y se recomienda utilizar alguno de los libros de apoyo como el Jensen[8] donde se realizan todas las demostraciones con detalle. La idea física principal es que vamos a pasar de una complicada ecuación de Schrödinger con \(N_e\) coordenadas, que no sabemos como resolver, a un problema más sencillo donde vamos a tener \(N_e\) ecuaciones de Schrödinger, una por cada electrón individual del sistema.

Definición del método

El método de Hartree-Fock tiene 2 características:

• 1. Es un método variacional, es decir, se va a proponer una función de onda para el estado fundamental, \(\Psi_e\), que dependerá de unos parámetros \(\{c\}\) y se obtendrá la energía del sistema evaluando el Hamiltoniano electrónico con esta función de onda y minimizando el resultado con respecto a los parámetros \(\{c\}\),

(122)\[\Psi_e(\{c\}) \Rightarrow E(\{c\})=\frac{\left\langle \Psi_e \right\vert \hat{H} \left\vert \Psi_e \right \rangle}{\left\langle \Psi_e \vert \Psi_e \right \rangle} \Rightarrow \frac{\delta E}{\delta c_i}=0,~\forall i\]

La cuestión clave es, ¿qué forma debe tomar la función de onda? Esta función es muy complicada ya que depende de 3\(N_e\) coordenadas. La idea que tuvo Hartree, en un artículo de 1928[9] (recién creada la mecánica cuántica, ¡el artículo de la ecuación de Schrödinger es de 1926[10]!) es proponer que esta función puede tratarse como un producto de las funciones de onda de cada uno de los electrones,

(123)\[\Psi_e(\vec{r}_1,\vec{r}_2,\vec{r}_3,...)\approx \psi_1(\vec{r}_1) \psi_2(\vec{r}_2) \cdots \psi_N(\vec{r}_N)\]

los parámetros \(\{c\}\) para Hartree tenían que ver con la forma espacial que tomaban los orbitales a un electrón \(\psi_i(\vec{r}_i)\). Por este motivo, la derivada con respecto a \(\{c\}\) en la Ec. (122) se utiliza para encontrar unas ecuaciones diferenciales que describen a los orbitales moleculares \(\psi_i\).

Aunque la manera en que Hartree ataca el problema es muy interesante, la función de onda que propone, Ec. (123), tiene muchas deficiencias. Como es bien conocido en mecánica cuántica los electrones deben:

-(i) ser partículas indistinguibles y en la función de onda de Hartree cada electrón tiene una función de onda (y por tanto una distribución espacial) bien definida

-(ii) son fermiones por lo que dos electrones no pueden tener el mismo número cuántico, expresado por el principio de exclusión de Pauli.

Es fácil comprobar que en la Ec. (123) no hay nada que impida tomar dos funciones de onda \(\psi_i\) y \(\psi_j\) exactamente iguales.

Fue V. Fock el que introdujo estos aspectos dentro de la función de onda de Hartree. Como veremos más abajo tener en cuenta la indistinguibilidad y el principio de exclusión da lugar a la aparición de un término de interacción, relativamente pequeño pero muy importante, que se denomina el intercambio. La persona que expresó esta función de onda en la forma moderna, que utilizamos hoy en día, fue John C. Slater.

• 2. La forma de la función de onda Hartree-Fock es el determinante de Slater, que mezcla, por filas y columnas, las coordenadas de los electrones (\(\vec{r}_i\)) con los índices de las funciones de onda (\(\psi_j\)),

(124)\[\begin{split}\Psi_e= \begin{vmatrix} \psi_1(\vec{r}_1) & \psi_2(\vec{r}_1) & \cdots &\psi_N(\vec{r}_1) \\ \psi_1(\vec{r}_2) & \psi_2(\vec{r}_2) & \cdots &\psi_N(\vec{r}_2) \\ \vdots & \vdots & \ddots &\vdots \\ \psi_1(\vec{r}_N) & \psi_2(\vec{r}_N) & \cdots &\psi_N(\vec{r}_N) \end{vmatrix}\end{split}\]

En esta forma, se verifica el principio de incertidumbre, dado que los electrones, que podemos identificar por sus coordenadas \(\vec{r}_i\) no están asignados a una función de onda particular \(\psi_j\). Del mismo modo, si eligiésemos dos funciones de ondas de los electrones con igual forma, \(\psi_i=\psi_j\), dos columnas del determinante serían linealmente dependientes y, como es bien conocido, el determinante sería nulo cumpliendo el principio de exclusión de Pauli.

En resumen, el método de Hartree-Fock tiene dos características, es variacional y la función de onda de prueba que se toma es un determinante de Slater.

Funciones de onda a un electrón y funciones de onda multielectrónicas

Es muy importante diferenciar los dos tipos de funciones de onda que aparecen en el método de Hartree-Fock. La primera es \(\Psi_e(\vec{r}_1,\vec{r}_2,\vec{r}_3,...)\), el determinante de Slater, que escribimos en mayúsculas y que representa el estado multielectrónico formado por los \(N_e\) electrones a la vez.

Por otro lado tenemos las funciones de onda monoelectrónicas o a un electrón que describen a los electrones de forma individual (nótese que esto es, claramente, una aproximación). En general consideramos que la función de onda a un electrón, \(\psi_i\) (en minúsculas), está formada por un producto de dos partes,

(125)\[\psi_i(\vec{r})=\phi_i(\vec{r})\sigma_i\]

la primera es la parte espacial \(\phi_i\) que depende de las coordenadas del electrón \(\vec{r}\). Su módulo al cuadrado caracteriza la distribución de carga (densidad espacial) del electrón e informa, por tanto, de la probabilidad de encontrar al electrón en alguna región del espacio,

(126)\[\rho_i(\vec{r})=\vert\psi_i(\vec{r})\vert^2=\vert \phi_i(\vec{r})\vert^2\]

la segunda parte es la función que describe el espín del electrón i, \(\sigma_i\), que se corresponde con el armónico esférico asociado a una función de momento angular \(s=1/2\) y proyección sobre el eje z positiva (\(s_z=+1/2\)) o negativa (\(s_z=-1/2\)),

(127)\[\begin{split}\left\vert \sigma_i\right\rangle= \left\vert s,~s_z\right\rangle =\begin{cases} \left\vert s=1/2, s_z=+1/2 \right\rangle &= \left\vert \alpha \right\rangle \\ \left\vert s=1/2, s_z=-1/2 \right\rangle &= \left\vert \beta \right\rangle \end{cases}\end{split}\]

Tal que,

(128)\[\begin{split}\hat{S}^2 \vert\alpha\rangle &= \hbar^2 \frac{1}{2}\left(\frac{1}{2}+1\right) \vert\alpha\rangle \\ \hat{S}_z \vert\alpha\rangle &= +\hbar \frac{1}{2} \vert\alpha\rangle \\ \hat{S}^2 \vert\beta\rangle &= \hbar^2 \frac{1}{2}\left(\frac{1}{2}+1\right) \vert\beta\rangle \\ \hat{S}_z \vert\beta\rangle &= -\hbar \frac{1}{2} \vert\beta\rangle \\\end{split}\]

Energía de un determinante de Slater

Para aplicar el método variacional debemos ahora calcular la energía de un determinante de Slater. El procedimiento matemático no es complicado, aunque sí algo tedioso, y se desarrolla por ejemplo en la página 59 de la Ref. [8]. Aquí nos centraremos en el resultado, que es el siguiente,

(129)\[E=\sum_i^N \left[ t_i + v_{en,i} + \sum_{j>i}^N \left(J_{ij}-K_{ij}\right) \right] + v_{nn}\]

En esta expresión tenemos, partiendo por lo más sencillo, la repulsión coulombiana entre dos núcleos,

(130)\[v_{nn}= \sum_\alpha \sum_{\beta>\alpha} \frac{Z_\alpha Z_\beta}{\vert\vec{R}_\alpha-\vec{R}_\beta\vert}\]

la suma de la energía cinética de los electrones, donde aparece la integral,

(131)\[t_i=\left\langle \psi_i \right\vert -\frac{1}{2}\vec{\nabla}_i^2 \left\vert\psi_i\right\rangle\]

que aporta la energía cinética del electrón en el orbital \(\psi_i\). Además contamos con el potencial atractivo entre el electrón en el orbital \(\psi_i\) con el núcleo \(\alpha\),

(132)\[v_{en,i}=\left\langle \psi_i \right\vert -\sum_\alpha \frac{Z_\alpha}{\vert\vec{R}_\alpha-\vec{r}_i\vert} \left\vert\psi_i\right\rangle.\]

Finalmente tenemos las energías de interacción entre electrones. Las hay de dos tipos, la directa,

(133)\[J_{ij}=\left\langle \psi_j (\vec{r}_2) \right\vert \left\langle \psi_i (\vec{r}_1) \right\vert \frac{1}{\vert\vec{r}_1 - \vec{r}_2\vert} \left\vert \psi_i(\vec{r}_1)\right\rangle\left\vert \psi_j(\vec{r}_2)\right\rangle=\int \int \frac{\vert \psi_i(\vec{r}_1)\vert^2\vert \psi_j(\vec{r}_2)\vert^2}{\vert\vec{r}_1 - \vec{r}_2\vert} d^3r_1 d^3r_2\]

y la de intercambio,

(134)\[K_{ij}=\left\langle \psi_{i} (\vec{r}_2) \right\vert \left\langle \psi_{j} (\vec{r}_1) \right\vert \frac{1}{\vert\vec{r}_1 - \vec{r}_2\vert} \left\vert \psi_i(\vec{r}_1)\right\rangle\left\vert \psi_j(\vec{r}_2)\right\rangle=\int \int \frac{ \psi_j^*(\vec{r}_1)\psi_i(\vec{r}_1) \psi_i^*(\vec{r}_2)\psi_j(\vec{r}_2)}{\vert\vec{r}_1 - \vec{r}_2\vert} d^3r_1 d^3r_2.\]

En el caso de la integral directa (J) podemos ver que se corresponde con la energía de interacción entre las densidades de carga \(\psi_i^2\) y \(\psi_j^2\), es decir, el potencial coulombiano repulsivo entre el electrón ocupando el orbital i y el j. Esta interacción aparece ya en el método de Hartree.

Mientras tanto la integral de intercambio, (K), que aparece con la introducción del principio de incertidumbre y el principio de exclusión, no tiene análogo clásico y es un efecto cuántico que tiene que ver con que las coordenadas de los electrones se intercambien en una de las integrales que aparecen en el potencial coulombiano directo.

Dado que la energía cinética y el potencial electrón núcleo dependen de, tan sólo, una coordenada electrónica se dice que son términos a un electrón mientras que las energías directa y de intercambio dependen de 2 coordenadas electrónicas y se llaman términos a dos electrones o bielectrónicos.

Ecuaciones de Hartree-Fock

Para aplicar el método variacional[4] debemos ahora derivar la energía con respecto a los parámetros en los que expresamos la función de onda. En el método de Hartree-Fock estos parámetros son la forma de las funciones de onda a un electrón, \(\psi_i\). Es decir, que consideramos a la energía como un funcional, es decir, una función de funciones y queremos hacer una derivada funcional,

(135)\[\delta E=\frac{\delta E}{\delta \psi_i}=0,~~ \forall i\]

para encontrar el mínimo de E, y por tanto, la forma de las funciones \(\psi_i\) que minimiza la energía de todo el sistema electrónico. Además la derivada, Ec. (135) debe hacerse manteniendo la norma de los orbitales \(\psi_i\) constante y haciendo que los orbitales \(\psi_i\) sean ortogonales entre sí (si fueran linealmente dependientes harían que el determinante de Slater fuese cero),

(136)\[\int \psi_i(\vec{r})\psi_j(\vec{r})d^3r= \delta_{ij}\]

Este desarrollo es, de nuevo, matemáticamente delicado[8] y nos centraremos en el resultado final que nos indica la condición que deben verificar las funciones \(\psi_i\) para cumplir con las Ecs. (135) y (136),

(137)\[\hat{h}(\vec{r})\psi_i(\vec{r}) = \varepsilon_i \psi_i(\vec{r}).\]

El conjunto de ecuaciones Ec. (137) (una por cada orbital \(\psi_i\)) se denominan ecuaciones de Hartree-Fock y describen el movimiento de cada uno de los electrones en una molécula o sólido. Como puede observarse las ecuaciones de Hartree-Fock son ecuaciones a un electrón, por lo que, a veces, esta técnica se denomina el método de los electrones independientes pero, como discutiremos más abajo este nombre es engañoso.

El Hamiltoniano a un electrón en las ecuaciones de Hartree-Fock tiene la siguiente forma,

(138)\[\hat{h}=\frac{1}{2}\vec{\nabla}^2 - \sum_\alpha \frac{Z_\alpha}{\vert\vec{r}-\vec{R}_\alpha\vert} + \sum_i \frac{\vert\psi_i\vert^2}{\vert \vec{r}-\vec{r_i}\vert} + v_{exc}\]

donde podemos reconocer el operador de energía cinética del electrón, seguido de su interacción coulombiana con todos los núcleos, la interacción coulombiana del electrón con la densidad de carga generada por todos los electrones y, finalmente, la interacción del electrón mediante el intercambio, con el resto de los electrones, que tiene la forma,

(139)\[v_{exc} \left\vert \psi_i (\vec{r}) \right\rangle = \sum_j \left\langle \psi_{j} (\vec{r}_2) \right\vert \frac{1}{\vert\vec{r} - \vec{r}_2\vert} \left\vert \psi_i(\vec{r}_2)\right\rangle \left\vert \psi_j(\vec{r})\right\rangle.\]

La energía de cada electrón individual, el autovalor \(\varepsilon_i\) en la Ec. (138), contiene también cada una de estas contribuciones,

(140)\[\varepsilon_i = t_i + v_{en,i} + \sum_{j}^N \left(J_{ij}-K_{ij}\right)\]

Es importante observar que la energía total no es la suma de la energía de cada uno de los electrones. De hecho la energía total del método Hartree-Fock puede expresarse en función de las energías de los electrones individuales del siguiente modo,

(141)\[E_{HF}= \sum_i \varepsilon_i -\frac{1}{2} \sum_{i,j}^N \left(J_{ij}-K_{ij}\right)+v_{nn}\]

El segundo sumando se llama la corrección por doble contaje (en inglés double counting) ya que la suma de energías a un electrón cuenta la interacción entre los electrones i y j dos veces, la primera cuando sumamos el término del electrón i, \(\varepsilon_i\), y después cuando sumamos la del electrón j, \(\varepsilon_j\) (ver Fig. 103). Es por ello que la corrección respecto a la suma de las energías de electrones individuales se debe a los términos a dos electrones y no a los términos a un electrón.

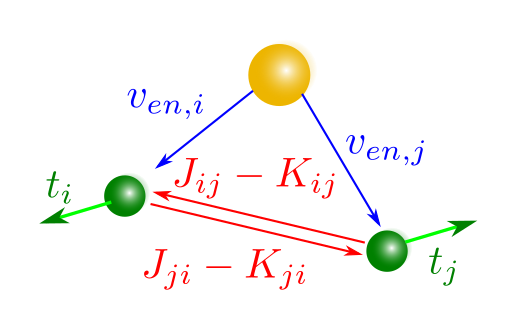
Fig. 103 Ilustración del doble contaje en las interacciones electrón-electrón, tanto directas \(J_{ij}\) como de intercambio \(K_{ij}\). Estas no aparecen en las interacciones a un electrón \(t_i\) o \(v_{en,i}\).

Algunas propiedades importantes

-1. Campo medio: El método de Hartree-Fock nos permite pasar de una ecuación de Schrödinger para \(N_e\) electrones a \(N_e\) ecuaciones para cada uno de los electrones del sistema. Es importante tener en cuenta que esto no quiere decir que los electrones no interaccionen entre sí. Si observamos el hamiltoniano de cada electrón,

(142)\[\begin{split}\hat{h}&=\frac{1}{2}\vec{\nabla}^2 - \sum_\alpha \frac{Z_\alpha}{\vert\vec{r}-\vec{R}_\alpha\vert} + \sum_i \frac{\vert\psi_i\vert^2}{\vert \vec{r}-\vec{r_i}\vert} + v_{exc}\\ v_{exc} \left\vert \psi_i (\vec{r}) \right\rangle &= \sum_j \left\langle \psi_{j} (\vec{r}_2) \right\vert \frac{1}{\vert\vec{r} - \vec{r}_2\vert} \left\vert \psi_i(\vec{r}_2)\right\rangle \left\vert \psi_j(\vec{r})\right\rangle\end{split}\]

podemos observar que un electrón interacciona con la suma de los potenciales creados por cada uno de los otros electrones, es decir, no ve a los electrones individuales pero sí lo hace a su campo medio (total).

-2. Autointeracción: Viendo las integrales a dos electrones Ec. (133) y (134) podemos observar que, evaluadas para el mismo orbital son iguales, es decir,

(143)\[J_{ii}=K_{ii}\]

por tanto, interacción coulombiana de un electrón consigo mismo, \(J_{ii}-K_{ii}\), es nula.

-3. Intercambio: La interacción de intercambio en la energía de Hartree-Fock reduce la energía (ver el signo negativo en la Ec. (129)). Aún así, podemos ver que la integral de intercambio, \(K_{ij}\), sólo es no nula cuando los electrones i y j tienen el mismo espín,

(144)\[\begin{split}K_{ij}&=\int \int \frac{ \phi_j^*(\vec{r}_1)\phi_i(\vec{r}_1) \phi_i^*(\vec{r}_2)\phi_j(\vec{r}_2)}{\vert\vec{r}_1 - \vec{r}_2\vert} d^3r_1 d^3r_2\int ds_1 \sigma_j^*(s_1) \sigma_i(s_1) \int ds_2 \sigma_i^*(s_2) \sigma_j(s_2)=\\ &=\delta_{\sigma_i \sigma_j} \int \int \frac{ \phi_j^*(\vec{r}_1)\phi_i(\vec{r}_1) \phi_i^*(\vec{r}_2)\phi_j(\vec{r}_2)}{\vert\vec{r}_1 - \vec{r}_2\vert} d^3r_1 d^3r_2\end{split}\]

Es decir, que el intercambio reduce las interacciones electrostáticas entre dos electrones que tienen ambos espín hacia arriba o ambos espín hacia abajo.

Problemas y ejemplos