Aproximación armónica y modos de vibración en un sólido

El caso de las vibraciones en un sólido es, sobre todo, una extensión de las vibraciones de una molécula, que se trataron en la Sec. vibraciones. Las bases son las mismas:

• A partir de la ecuación del movimiento de los núcleos:

(384)\[\left(\hat{T}_n + E_i(R)\right)\Psi_n^{\alpha}=E_{i,\alpha}\Psi_n^{\alpha}\]

• Se realiza una transformación a coordenadas pesadas por la masa, \(\tilde{R}_{\alpha,x}\):

(385)\[\tilde{R}_{\alpha,x} = \sqrt{M_\alpha} R_{\alpha,x}\]

• Se expande la superficie de energía del estado fundamental, \(E_i\), hasta segundo orden alrededor del mínimo de energía usando las coordenadas reducidas en masa,

(386)\[E_{i}(\{\tilde{R}\})\approx E_{i}(\tilde{R}_0)+\sum_{\alpha^\prime x} 0 \tilde{R}_{\alpha^\prime,x} + \frac{1}{2}\sum_{\alpha^\prime x,\beta^\prime y} \left.\frac{d^2 E_i}{d\tilde{R}_{\alpha^\prime,x} d\tilde{R}_{\beta^\prime,y}} \right\vert_{R=R_0}\tilde{R}_{\alpha^\prime,x} \tilde{R}_{\beta^\prime,y} + \cdots\]

obteniéndose la matriz Hessiana.

(387)\[\mathcal{H}=\frac{1}{2} \left. \frac{d^2 E_i}{d\tilde{R}_{\alpha^\prime,x} d\tilde{R}_{\beta^\prime,y}} \right\vert_{R=R_0} \]

• Diagonalizando esta matriz podemos obtener los autovalores, \(\omega_\alpha^2\), que son las frecuencias de vibración al cuadrado y los modos normales (autovectores),

(388)\[ Q_\alpha = \sum_{\alpha^\prime,x} c_{\alpha, \alpha^\prime x} \tilde{R}_{\alpha^\prime,x}\]

que nos permiten separar el Hamiltoniano nuclear en una suma de modos independientes,

(389)\[ \left(\hat{T}_n + E_i(\{\vec{R}\})\right)\Psi_n^{\gamma}\approx \sum_{\alpha} \left(\frac{\hbar^2}{2} \frac{d^2}{dQ_\alpha^2}+\frac{1}{2}\omega_\alpha^2 Q_\alpha^2\right)\Psi_n^{\gamma} = E_{i,\gamma}\Psi_n^{\gamma}\]

La pregunta clave en este proceso es, ¿qué forma tienen los modos normales de un sólido?. Una (importante) dificultad que no se ha tenido en cuenta en el procedimiento anterior es que los sólidos contienen un enorme número de átomos. Esto, claramente, es un impedimento para diagonalizar la matriz Hessiana. En la próxima sección veremos como podemos resolver esta pregunta.

Modos normales en un sólido

La manera de obtener los modos normales, diagonalizando la matriz Hessiana, difiere poco si lo tratamos clásica o cuánticamente. De hecho, el Hamiltoniano cuántico, dado por la Ec. (384), se podría escribir clásicamente a través de la energía mecánica de un sistema de bolas conectadas por muelles. En la siguiente sección nos vamos a fijar en como escribir la energía potencial elástica asociada a un sólido.

Energía elástica de un sólido

Para comenzar esta sección vamos a definir una configuración de referencia del sólido. Si suponemos que el sólido se encuentra en el mínimo de su energía potencial, los átomos ocupan su posición de equilibrio. Para calcular la energía elástica del sólido vamos a tomar esta geometría como referencia y añadir el incremento en la misma cuando los átomos se desvían de estas posiciones de equilibrio. Como podemos ver en la Fig. 233 a estas distorsiones las denotaremos por un vector \(\vec{u}\) que, como veremos más abajo, dependerá de la celda que ocupa el átomo (n en la figura) y un índice que indicará a que átomo de la celda unidad nos referimos (este índice no se incluye en la figura ya que se trata de una cadena con un único átomo de motivo).

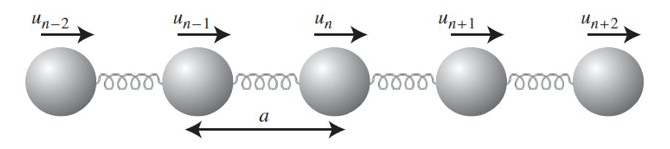
Fig. 233 Ilustración de un sólido periódico sencillo cuyos átomos se muestran como esferas grises, separadas por el parámetro de malla, \(a\). La energía elástica de este cristal se aproxima mediante interacciones de primeros vecinos representados aquí mediante muelles.

Por tanto, la posición de un átomo de la red la escribiremos como,

(390)\[\vec{r}_{\vec{R}_\alpha, \alpha} = \vec{R}_\alpha + \vec{\tau}_\alpha + \vec{u}_{\vec{R}_\alpha,\alpha} \]

donde \(\vec{R}_\alpha\) es el vector de la red de Bravais que caracteriza la celda donde se encuentra el átomo, \(\tau_\alpha\) es el vector que caracteriza la posición del átomo dentro de la celda unidad en la geometría de referencia y \(\vec{u}_{\vec{R}_\alpha,\alpha}\) es el vector que indica cuanto se ha movido ese átomo particular respecto al punto de equilibrio.

Ahora podemos definimos la matriz de constantes de fuerza como,

(391)\[K_{\alpha x,\beta y}= \left. \frac{d^2 E_i}{d u_{\alpha,x} du_{\beta,y}} \right\vert_{R=R_0} \]

podemos definir la energía potencial elástica de una molécula como,

(392)\[U_{\text{molécula}}= \frac{1}{2} \sum_{\alpha x, \beta y} K_{\alpha x,\beta y} u_{\alpha,x} u_{\alpha, y}.\]

Es sencillo darse cuenta que la matriz de constantes de fuerza, Ec. (391) está fuertemente relacionada con el Hessiano, Ec. (388) a través de un cambio a coordenadas reducidas.

Si estamos tratando un sólido, podemos imaginarnos, por ejemplo, una cadena infinita, como la mostrada en la Fig. 233. Como tratamos en el capítulo de estructura, en un sólido necesitamos 2 argumentos para definir la estructura, la red y el motivo. Por tanto, en vez de sumar sobre átomos \(\alpha\) en el sólido resulta más claro cambiar ese sumatorio en la Ec. (392) por uno sobre las posiciones de la red de Bravais y los átomos en la celda primitiva:

(393)\[U_{\text{sólido}}= \frac{1}{2} \sum_{\vec{R}_\alpha}\sum_{\alpha}^{\text{UC}} \sum_{x_\alpha}\sum_{\vec{R}_\beta} \sum_{\beta}^{\text{UC}} \sum_{x_\beta} K_{\alpha \vec{R}_\alpha x_\alpha, \beta \vec{R}_\beta x_\beta} R_{\alpha \vec{R}_\alpha x_\alpha} R_{\beta \vec{R}_\beta x_\beta}.\]

Ecuación de movimiento de Newton

Una vez que conocemos la energía elástica podemos, seguidamente, escribir la ecuación de Newton para cada uno de los átomos dentro de una celda. No vamos a repetir estas ecuaciones para cada celda ya que, claramente, el movimiento de un cierto átomo \(\alpha\) en una celda tiene que estar relacionado con como se mueve ese átomo en otra celda, ya que existe una simetría de traslación que los relaciona.

La ecuación de Newton para el átomo \(\alpha\) en la celda unidad es,

(394)\[M_\alpha \vec{a}_{\alpha} = \vec{F}_\alpha\]

Sabiendo que la aceleración es la segunda derivada de la posición con el tiempo y que la fuerza está relacionada con la energía elástica del siguiente modo,

(395)\[F_{\alpha,x} = - \frac{\partial U}{\partial u_{\alpha,x}}\]

tenemos que,

(396)\[M_\alpha \ddot{R}_{\alpha,x} = - \frac{\partial U}{\partial R_{\alpha,x}} = - \sum_{\vec{R}_\beta} \sum_{\beta}^{\text{UC}} \sum_{x_\beta} K_{\alpha \vec{R}_\alpha x_\alpha, \beta \vec{R}_\beta x_\beta} R_{\beta \vec{R}_\beta x_\beta}\]

donde \(\alpha\) son todos los átomos de la celda unidad. Esta ecuación puede expresarse de forma matricial como,

(397)\[\mathcal{M}\ddot{\vec{u}} = - \mathcal{K}\vec{u}\]

donde las matrices de masa, \(\mathcal{M}\) y de constantes de fuerza \(\mathcal{K}\) son matrices que tienen \(N_\alpha \times \) dimensión del problema filas y columnas mientras que \(\vec{u}\) es un vector con ese tamaño. En particular, la matriz de masas, \(\mathcal{M}\), es diagonal y sus valores contienen la masa de los átomos.

Solución de la ecuación de Newton

La solución de la Ec. (397) es,

(398)\[\vec{u}_{\vec{k},\vec{R}_\alpha}=\vec{\varepsilon} e^{i\vec{k}\cdot\vec{R}_\alpha - \omega t}\]

Para comprobarlo sustituímos la Ec. (398) en la ecuación de Newton, Ec. (397) y obtenemos,

(399)\[M\omega_k^2 \vec{\epsilon}_k=K_k\vec{\epsilon}_k\]

Podemos observar que tanto las frecuencias, \(\omega_k\), el vector del modo, \(\vec{\epsilon}_k\), como la matriz de constantes de fuerza que aparece en la solución, \(K_k\), dependen ahora del vector de onda \(\vec{k}\) que aparece en la Ec. (399). En particular, la matriz de constantes de fuerza dependiente del vector de ondas (como veremos en la siguiente sección realmente es una matriz en el espacio recíproco) es la tranformada de Fourier de la matriz de constantes de fuerza en el espacio directo (dependiente de un vector de la red de Bravais \(\Delta \vec{R}\)),

(400)\[K_{\vec{k}}=\sum_{\vec{\Delta \vec{R}} } K_{\Delta\vec{R}} e^{i\vec{k}\cdot \Delta\vec{R}} \rightarrow M^{-1} K_k \vec{\epsilon} = \omega_k^2 \vec{\epsilon} \longrightarrow \mathcal{D}_k \vec{\epsilon} = \omega_k^2 \vec{\epsilon}\]

Tomando ahora la Ec.(399) es sencillo relacionarla con la solución del problema vibracional en moléculas, Ec. (346),

(401)\[K_k\vec{\epsilon}_k=M\omega_k^2 \vec{\epsilon}_k \rightarrow M^{-1} K_k \vec{\epsilon} = \omega_k^2 \vec{\epsilon} \longrightarrow \mathcal{H}_k \vec{\epsilon} = \omega_k^2 \vec{\epsilon}\]

donde podemos observar que multiplicar por la inversa de la matriz de masas hace el efecto de la transformación a coordenadas reducidas por la masa y que \(\mathcal{H}_k\) es la matriz Hessiana en la Ec. (346).

Interpretación de las vibraciones

En la sección anterior hemos probado que la Ec. (398) era la solución de la ecuación de Newton para las vibraciones de un sólido. En esta sección lo que vamos a buscar es dar un significado a esta ecuación y, en particular, al vector \(\vec{k}\) que aparece en la misma y que, como veremos, está fuertemente relacionado con la red recíproca.

Teorema de Bloch

La forma de la solución de la ecuación de Newton tiene que ver con la simetría traslacional del sólido y es la consecuencia de un teorema fundamental para la mecánica cuántica de los sólidos que es el teorema de Bloch. Este teorema no es otra cosa que la Ec. (209), que representa el efecto de aplicar un operador de simetría \(\hat{R}\) sobre una función de onda del sistema,

(402)\[\hat{R}\Psi(\vec{r},\vec{R})=e^{i\varphi}\Psi(\vec{r},\vec{R}^\prime)\]

pero aplicada a las traslaciones de los sólidos, que son un tipo de simetría.

Veamos como cambia el vector \(\vec{u}\) cuando le aplicamos una traslación.

(403)\[\hat{T}\vec{u}_{\vec{k},\vec{R}_\alpha}=\vec{u}_{\vec{k},\vec{R}_\alpha+\vec{T}}=\vec{\varepsilon} e^{i\vec{k}\cdot(\vec{R}_\alpha+\vec{T}) - \omega t} = e^{i\vec{k}\cdot\vec{T}}\vec{u}_{\vec{k},\vec{R}_\alpha}\]

que es, precisamente, lo que dice la Ec. (402). Es decir, la solución escogida es válida porque tiene las propiedades necesarias para verificar la simetría traslacional del sólido.

Relación con la red recíproca

La siguiente pregunta que debemos hacernos es que valores puede tomar \(\vec{k}\). Este vector se encuentra como parte de la potencia de una exponencial compleja donde \(\vec{T}\) es una posible translación en un sólido, es decir, un vector de la red de Bravais. Vamos a intentar, ahora, revelar la periodicidad inherente a cualquier exponencial compleja. Para ello vamos a redefinir el vector de ondas como,

(404)\[\vec{k}=\vec{k}_{BZ}+\vec{G}\]

donde \(\vec{k}_{BZ}\) es el vector \(\vec{k}\) de la zona donde la solución está únicamente definida (como veremos será la zona de Brillouin (BZ)) y \(\vec{G}\) el vector que dicta la periodicidad. Sustituyendo la Ec. (404) en la exponencial de la Ec.(403) tenemos,

(405)\[ e^{i\vec{k}\cdot\vec{T}}=e^{i\left(\vec{k}_{BZ}+\vec{G}\right)\cdot\vec{T}}=e^{i\left(\vec{k}_{BZ}\vec{T}+\vec{G}\vec{T}\right)} =e^{i\vec{k}_{BZ}\vec{T}}e^{i\vec{G}\vec{T}}\]

dado que queremos que \(\vec{k}_{BZ}\) defina la solución única mientras que \(\vec{G}\) defina la periodicidad de esta solución imponemos que la última exponencial debe valer 1 por lo que tenemos,

(406)\[ \vec{G}\vec{T}=2\pi\]

Teniendo en cuenta que \(\vec{T}\) es un vector de la red de Bravais observamos que \(\vec{G}\) en la Ec.(406) es, precisamente, la definición de los vectores de la red recíproca. Por tanto, \(\vec{k}_{BZ}\) es un vector restringido a una celda unidad de la red recíproca que, normalmente, se toma como la primera zona de Brillouin.

Podemos comprobar como si a nuestra solución le sumamos un vector de la red recíproca, \(\vec{g}\), las frecuencias no varían,

(407)\[\begin{split}\omega^2(k+g)&=-\sum_{n} \mathcal{D}(n)e^{i(k+g)na}=\underbrace{-\sum_{n} \mathcal{D}(n)e^{ikna}e^{i2\pi mn}}_{g=\frac{2\pi}{a}m, m\in\mathcal{Z}}\\ &=-\sum_{n} \mathcal{D}(n)e^{ikna}=\omega^2(k).\end{split}\]

Condiciones periódicas de Born-von Karman

Imaginemos ahora que podemos obtener un sólido periódico, en una dimensión por simplicidad, a unir, en forma de círculo, el principio y final de una cadena finita (ver Fig. 234) que contiene N celdas de nuestro cristal. A este procedimiento se le denomina imponer las condiciones periódicas de Born-von Karman.

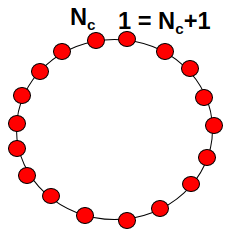
Fig. 234 Ilustración del uso de las condiciones periódicas de contorno de Born-von Karman en una cadena lineal que contiene N celdas unidad. El proceso une la primera (n=1) y la última celda (n=N) de modo que forman un círculo. Este proceso podría extenderse a dos dimensiones, lo que daría lugar a una cadena periódica con forma toroidal o en 3 dimensiones (con una extensión de una superficie toroidal tridimensional sumergida en un espacio de 4 dimensiones).

Cada una de las celdas tiene una longitud igual al parámetro de malla, \(a\), por lo que la longitud del cristal es \(L=Na\). Si ahora consideramos las vibraciones de los átomos en esta cadena periódica tenemos que las longitudes de onda no pueden tener un valor arbitrario. En particular, \(\lambda\) tiene que ser un divisor entero de la longitud total de la cadena, L (ver Fig. 235),

(408)\[L = n \lambda_n .\]

donde n puede valer entre cero y N-1 (o entre 1 y N, ver Fig. 234). Por lo que podemos escribir ahora el vector de ondas.

(409)\[k_n = \frac{2\pi}{\lambda_n} = \frac{2\pi}{L}n\]

Sustituyendo ahora el valor de L en función del parámetro de mallas tenemos,

(410)\[k_n = \frac{2\pi}{\lambda_n} = \frac{2\pi}{L}n = \frac{2\pi}{a} \frac{n}{N}.\]

En esta expresión podemos observar que \(2\pi/a\) es, precisamente, la longitud de la celda unidad en el espacio recíproco y n/N es un factor que toma valores entre 0 y N-1/N. Si ahora imaginamos que la cadena es muy grande el paso que mide ese factor se va haciendo más pequeño y vemos que el vector \(k_n\) define un continuo de valores entre 0 y \(2\pi/a\), es decir, nos indica claramente, como hemos encontrado antes que los vectores \(k_n\) toman valores dentro de una celda unidad del espacio recíproco. Si en vez de variar n entre 0 y N-1 lo hicieramos variar entre -N/2 y N/2 tendríamos que \(k_n\) se corresponde con un vector dentro de la primera zona de Brillouin (lo que es completamente equivalente a lo que indicabamos anteriormente).

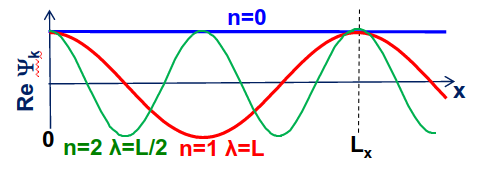
Fig. 235 Cuando consideramos una cadena con las condiciones de contorno de Born-von Karman las ondas deben volver a su valor inicial cuando llegan al final de la cadena. Esto da lugar a la aparición de ondas con longitud de onda bien definida que se suelen definir modos normales de vibración de la cadena.

Problems and solution examples