Molécula de agua

Molécula de agua#

Introducción#

La molécula de agua (\(H_2O\)) es muy sencilla, estando formada por un átomo de oxígeno y dos de hidrógeno (ver Fig. 173). Su estructura angular se caracteriza por un pertenecer al grupo \(C_{2v}\) donde el eje principal bisecta el ángulo H-O-H.

../_images/water_molecule.jpg — Fig. 173 Representación gráfica de la molécula de agua. El átomo de oxígeno está representado por una esfera roja y los de hidrógeno por esferas pequeñas blancas. El ángulo entre los hidrógenos y el oxígeno es, aproximadamente, 109\(^o\).#

La tabla de caracteres del grupo \(C_{2v}\) se presenta en la Fig. 174.

../_images/c2v_table.png — Fig. 174 Tabla de caracteres del grupo puntual \(C_{2v}\) al que pertenece la molécula de agua en su mínimo de energía.#

Construcción de la base#

Seguidamente buscamos los orbitales de valencia de la molécula. Cada átomo de hidrógeno contribuye con un orbital 1s mientras que el átomo de oxígeno tiene como orbitales de valencia el 2s y los 2p (\(p_x\), \(p_y\) y \(p_z\)). En la primera fila de la Fig. 175 se muestra una representación gráfica donde los lóbulos positivos se muestran en azul y los negativos en amarillo.

Simetrización de la base#

Lo siguiente que deseamos hacer es representar las diferentes operaciones del grupo \(C_{2v}\) (listadas en la tabla de caracteres, Fig. 174) usando la base dada anteriormente.

Empezamos por la rotación alrededor del eje principal (\(C_2\)). En la Fig. 175 se muestra como cambian los orbitales con este giro.

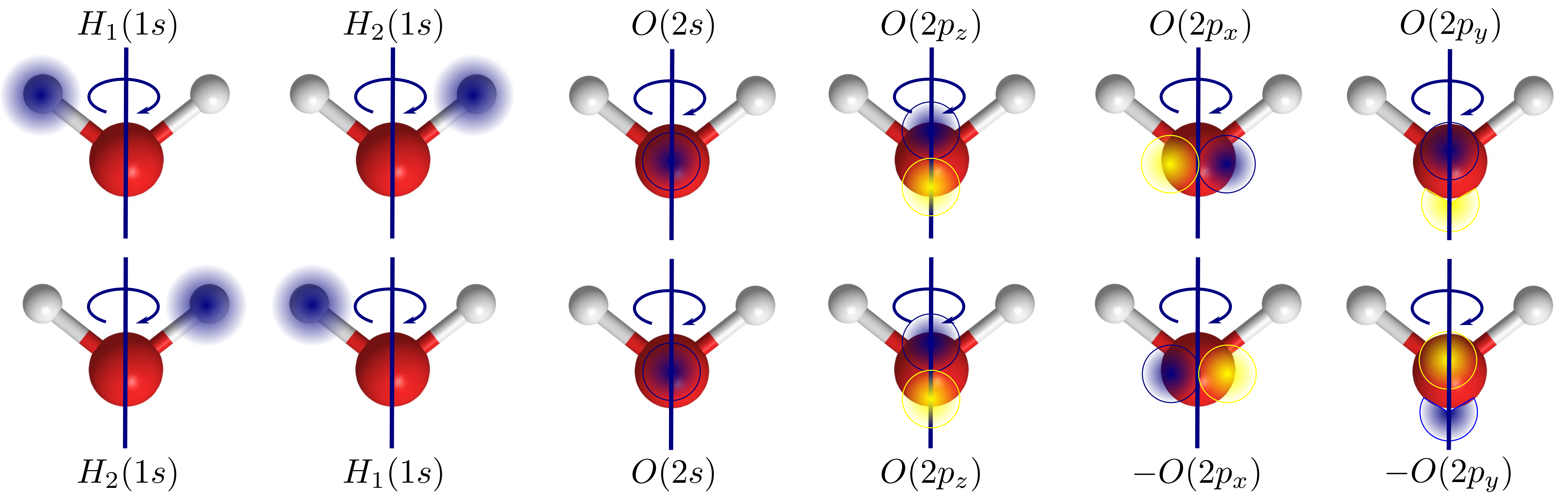
../_images/h2o_c2_symm_op.png — Fig. 175 Ilustración de las funciones de base iniciales del problema del agua (primera fila) y como cambian cuando les aplicamos una operación \(C_2\).#

Cuando escribimos la matriz asociada al \(C_2\) tenemos:

(300)#\[\begin{split}C_2= \begin{pmatrix} 0 & 1 & 0 & 0 & 0 & 0\\ 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & -1 & 0\\ 0 & 0 & 0 & 0 & 0 & -1\\\end{pmatrix} \rightarrow \chi(I)=0\end{split}\]

Se puede actuar de igual modo con las operaciones de simetría de reflexión en el plano de la molécula, Fig. 176.

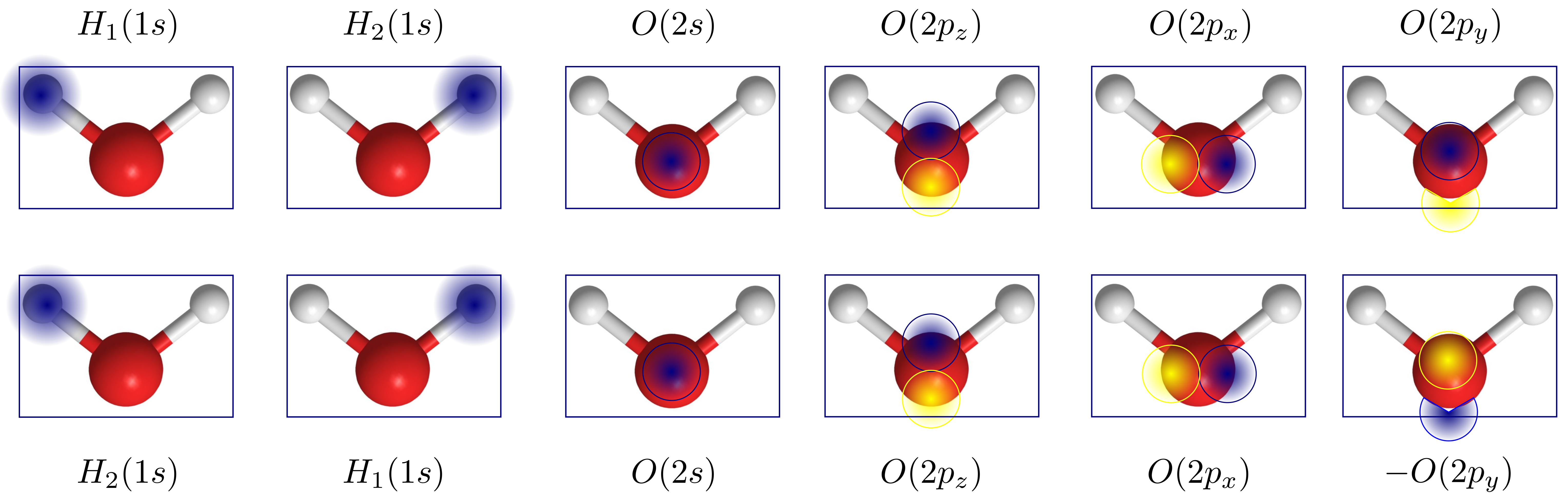
../_images/h2o_sigma_symm_op.png — Fig. 176 Ilustración de la superficie de energía de la molécula de hidrógeno y sus niveles cuánticos calculados según la aproximación armónica.#

(301)#\[\begin{split}\sigma_V= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & -1\\\end{pmatrix} \rightarrow \chi(I)=4\end{split}\]

y, trivialmente, se pueden obtener del plano perpendicular a la molécula,

(302)#\[\begin{split}\sigma_V= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & -1\\\end{pmatrix} \rightarrow \chi(I)=4\end{split}\]

y la identidad,

(303)#\[\begin{split}\sigma_V= \begin{pmatrix} 1 & 0 & 0 & 0 & 0 & 0\\ 0 & 1 & 0 & 0 & 0 & 0\\ 0 & 0 & 1 & 0 & 0 & 0\\ 0 & 0 & 0 & 1 & 0 & 0\\ 0 & 0 & 0 & 0 & 1 & 0\\ 0 & 0 & 0 & 0 & 0 & 1\\\end{pmatrix} \rightarrow \chi(I)=6\end{split}\]

Con estos operadores podemos observar que la parte de las matrices de los orbitales del oxígeno están automáticamente en cajas, por lo que podemos identificar la irrep a la que pertenecen, \(O(2s)\rightarrow a_1\), \(O(2p_z)\rightarrow a_1\), \(O(2p_x)\rightarrow b_1\), \(O(2p_y)\rightarrow b_2\) mientras que los orbitales del hidrógeno requieren un poco más de trabajo.

Aplicando las fórmulas que nos indican el número de irreps de cada tipo que generan las subcajas asociadas a los orbitales del hidrógeno tenemos que generan una irrep \(a_1\) y una irrep \(b_1\). Usando los proyectores obtenemos:

(304)#\[\phi(a_1)=H_+(1s)=\frac{1}{\sqrt{2}} \left(H_1(1s)+H_2(1s)\right)\]

(305)#\[\phi(b_1)=H_-(1s)=\frac{1}{\sqrt{2}} \left(H_1(1s)-H_2(1s)\right)\]

La representación gráfica de estas funciones se encuentra en la Fig. 177.

../_images/h2o_symm_basis.png — Fig. 177 Ilustración de la superficie de energía de la molécula de hidrógeno y sus niveles cuánticos calculados según la aproximación armónica.#

Es fácil comprobar que los nuevos orbitales son buenas funciones de la simetría (ver, por ejemplo, la Fig. 178).

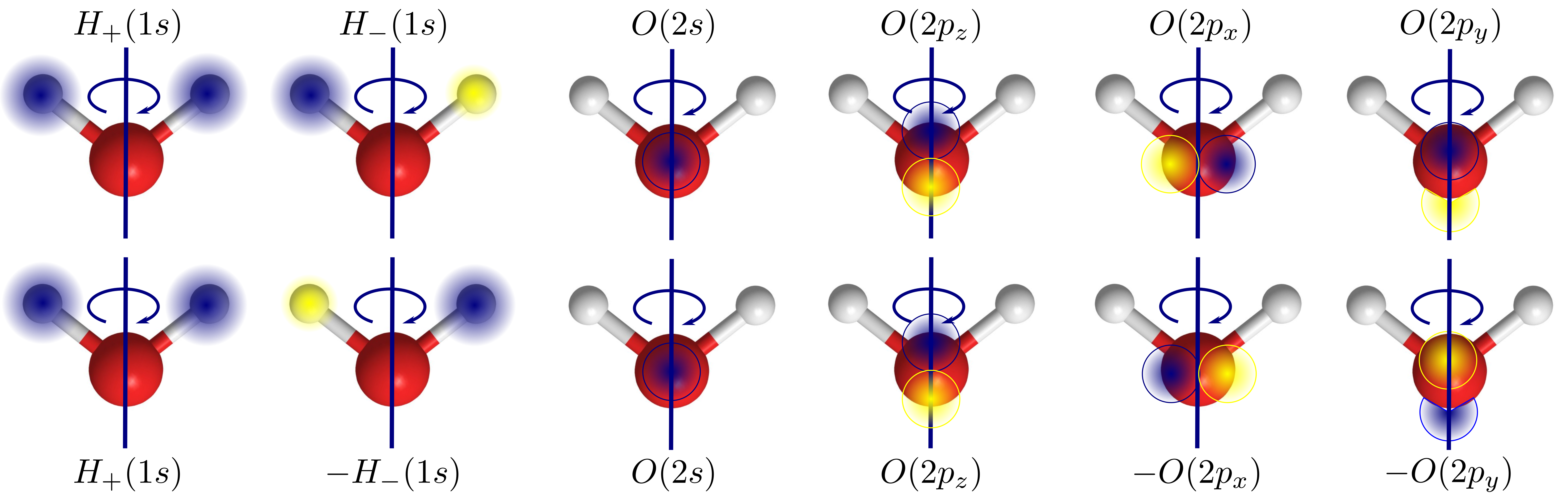
../_images/h2o_c2_symm_op_b.png — Fig. 178 Ilustración de la superficie de energía de la molécula de hidrógeno y sus niveles cuánticos calculados según la aproximación armónica.#

Hamiltoniano#

En la base inicial \(\{H_1(1s),H_2(1s),O(2s),O(2p_x),O(2p_y),O(2p_z)\}\) el Hamiltoniano tiene la forma,

(306)#\[\begin{split}H= \begin{pmatrix} \varepsilon_H & \gamma_{HH} & \gamma_{Hs} & 0 & -\gamma_{Hx} & \gamma_{Hz}\\ \gamma_{HH} & \varepsilon_H & \gamma_{Hs} & 0 & \gamma_{Hx} & \gamma_{Hz}\\ \gamma_{Hs} & \gamma_{Hs} & \varepsilon_{O(2s)} & 0 & 0 & 0\\ 0 & 0 & 0 & \varepsilon_{O(2p)} & 0 & 0\\ -\gamma_{Hx} & \gamma_{Hx} & 0 & 0 & \varepsilon_{O(2p)} & 0\\ \gamma_{Hz} & \gamma_{Hz} & 0 & 0 & 0 & \varepsilon_{O(2p)}\\\end{pmatrix} \end{split}\]

donde hemos diferenciado la interacción entre orbitales 1s del hidrógeno (\(\gamma_{HH}\)) y la interacción de estos últimos con los orbitales 2s (\(\gamma_{Hs}\)), 2p\(_x\) (\(\gamma_{Hx}\)) y 2p\(_z\) (\(\gamma_{Hz}\)) del oxígeno. La interacción entre el 2p\(_y\) y el 1s del hidrógeno es nula debido a que estos orbitales son ortogonales.

Cuando usamos la base simetrizada \(\{H_+(1s),O(2s),O(2p_z),O(2p_y),H_-(1s),O(2p_x)\}\) cambia a:

(307)#\[\begin{split}H= \begin{pmatrix} \varepsilon_H+\gamma_{HH} & \sqrt{2}\gamma_{Hs} & \sqrt{2}\gamma_{Hz} & 0 & 0 & 0\\ \sqrt{2}\gamma_{Hs} & \varepsilon_{O(2s)} & 0 & 0 & 0 & 0\\ \sqrt{2}\gamma_{Hz} & 0 & \varepsilon_{O(2p)} & 0 & 0 & 0\\ 0 & 0 & 0 & \varepsilon_{O(2p)} & 0 & 0\\ 0 & 0 & 0 & 0 & \varepsilon_H-\gamma_{HH} & \sqrt{2}\gamma_{Hx}\\ 0 & 0 & 0 & 0 & \sqrt{2}\gamma_{Hs} & \varepsilon_{O(2p)}\\\end{pmatrix} \end{split}\]

donde podemos observar que la función del hidrógeno \(a_1\) (\(H_+\)) puede interaccionar con los orbitales \(a_1(2s)\) y \(a_1(p_z)\) mientras que la \(b_1\) puede interaccionar con \(b_1(p_x)\)

Diagonalizando las cajas \(a_1\), \(b_1\) y \(b_2\) se obtiene el siguiente esquema de niveles moleculares:

../_images/h2o_molorb.png — Fig. 179 Esquema cualitativo de los orbitales moleculares del agua. Se puede observar que el nivel atómico del oxígeno 2s se encuentra mucho más profundo que los que los niveles 2p e H(1s). Los niveles \(a_1\) producen un nivel muy enlazante (principalmente oxígeno 2s) otro que es algo enlazante con una mezcla \(p_z\) - hidrógeno y otro muy antienlazante asociado a los orbitales H(1s) con mezclas de 2s y 2p\(_z\). El orbital con carácter \(b_1\) en el diagrama es no enlazante (correspondiente al orbital 2p\(_y\)) mientras que los orbitales en el plano \(H_-\) y 2p\(_x\) dan lugar en el diagrama a los orbitales b\(_2\) (uno enlazante y otro antienlazante). Notesé que en el dibujo se ha tomado el eje x y el eje y de forma diferente al desarrollo teórico. Esto sólo cambia las etiquetas x-y, b\(_1\)-b\(_2\) entre sí.#

Podemos observar que los orbitales ocupados \(2a_1\) y \(1b_2\) son claramente enlazantes, el \(3a_1\) es débilmente enlazante y el \(1b_1\) es no enlazante. Por tanto, el orden de enlace es, aproximadamente, 2, 1 por cada cada enlace sencillo hidrógeno-oxígeno.