Interacción luz-materia

La principal herramienta que tenemos para conocer el mundo microscópico es la luz, entendiendo el término en el sentido de radiación electromagnética, donde midiendo donde la materia absorbe (o emite) podemos extraer información sobre los niveles cuánticos. A pesar de la gran importancia de esta sección, nos vamos a limitar a entender los aspectos más generales de la interacción entre la luz y la materia desde el punto de vista cuántico. Para ello describiremos el campo de forma clásica (lo que es, claramente, una aproximación) y la materia de forma cuántica. Además usaremos una simplificación fundamental que es la llamada aproximación dipolar, donde, esencialmente, supondremos que la longitud de onda del campo es mucho mayor que el tamaño del sistema que observa esta radiación. Esto nos permitirá describir de forma relativamente sencilla los experimentos más básicos de espectroscopia, los de absorción.

Experimento de absorción

En un experimento de absorción, del que se muestra un esquema en la Fig. 222, se utiliza una fuente luminosa, representada por una esfera amarilla brillante. Para conocer la intensidad a la que la fuente emite en cada frecuencia utilizamos un monocromador. El monocromador más sencillo lo podemos visualizar como un prisma óptico que, a partir de un haz de luz blanca, hace que los rayos de diferente frecuencia (color) refracten a lo largo de direcciones diferentes (lo que visualizamos como un arco iris). Esto permite medir la intensidad de cada color de forma separada.

En la parte inferior de la figura se muestra como se mide un espectro de referencia, es decir, la intensidad propia de cada frecuencia de la luz que emite la fuente sin hacerlo pasar por la muestra. Si ahora medimos la intensidad de la luz, por canal de frecuencia, una vez que hemos hecho pasar el haz por la muestra y lo comparamos con nuestro espectro de referencia (restando este último del primero), obtendremos el espectro de absorción de la muestra. Si en vez de medir directamente el haz que atraviesa la muestra medimos en otra dirección podríamos obtener un espectro de emisión (aquí habría que tener cuidado con la luz difundida dentro de la muestra que no sería parte de este espectro).

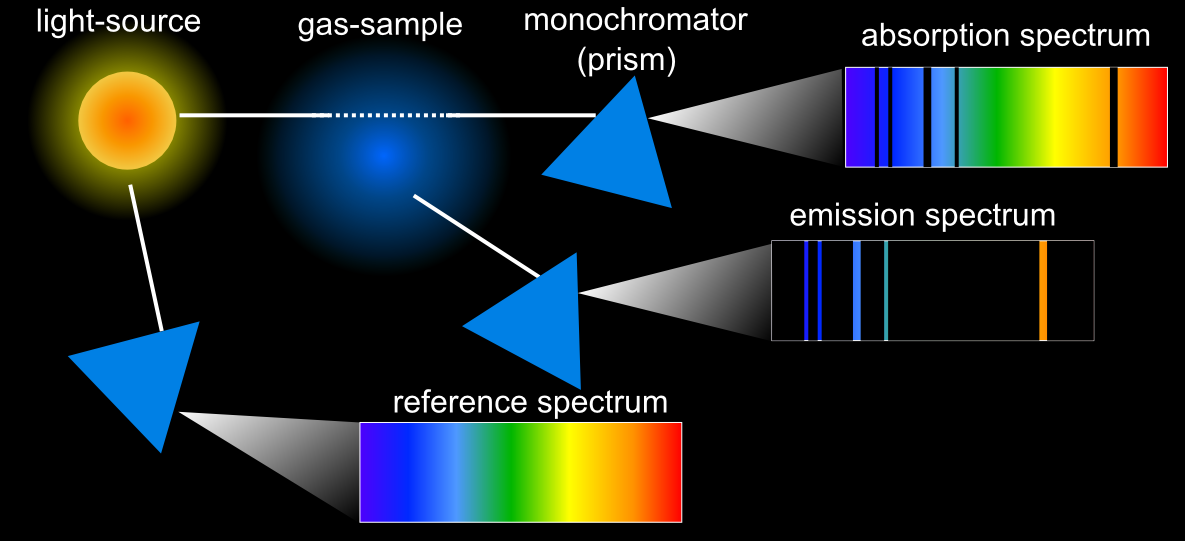
Fig. 222 Ilustración de un experimento de absorción. Si la luz se hace pasar por un moncromador (representado por un prisma triangular azul) se puede obtener un espectro de referencia que se compara con el que se obtiene al pasar la luz por una muestra (parte superior de la figura). El material absorbe (quite) intensidad de algunas de las líneas, dando lugar al espectro de absorción.

La pregunta principal que queremos responder en esta sección es, ¿qué frecuencias observaríamos en el espectro de absorción para una molécula y que intensidad tendrían los picos de ese espectro?.

Radiación electromagnética y la interacción con la materia

Veamos ahora como describir la radiación electromagnética. Aquí, como se ha indicado más arriba, nos vamos a limitar a una descripción clásica de la luz. A partir de las ecuaciones de Maxwell se pueden encontrar unas ecuaciones de onda para el campo eléctrico y el magnético,

(357)\[\begin{split}\mu_0\varepsilon_0 \frac{\partial^2 \vec{E}}{\partial t^2}-\vec{\nabla}^2\vec{E}=0\\ \mu_0\varepsilon_0 \frac{\partial^2 \vec{B}}{\partial t^2}-\vec{\nabla}^2\vec{B}=0.\end{split}\]

Cuyas soluciones son,

(358)\[\begin{split}\vec{E}=\vec{E}_0 e^{i(kz-\omega t)}\vec{u}_x\\ \vec{B}=\frac{\vec{E}_0}{c} e^{i(kz-\omega t)}\vec{u}_y\end{split}\]

donde podemos ver que la luz está formada por un campo eléctrico y otro magnético oscilando a cierta frecuencia angular \(\omega\) y una longitud de onda asociada \(\lambda\). Estos campos son perpendiculares entre sí y a la propagación de la onda (la radiación electromagnética forma una onda transversal), tal y como se muestra en la Fig. 223.

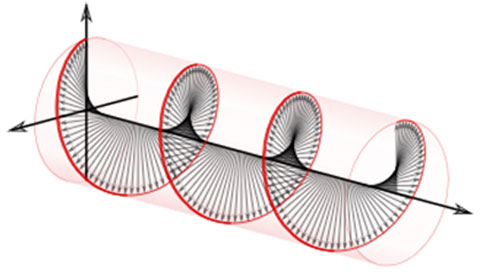
Fig. 223 Los campos eléctricos y magnéticos oscilan de forma perpendicular a la dirección de propagación, dando lugar a diferentes polarizaciones (Figura obtenida de la Wikipedia).

Cuando una molécula se expone a radiación electromagnética se ve sumergida en un campo eléctrico y otro magnético oscilantes, tanto espacial como temporalmente, y, para tener en cuenta su efecto, tendremos que resolver la ecuación de Schrödinger, tanto electrónica como nuclear, teniendo en cuenta estos campos.

Como es fácil de imaginar intentar esta resolución directamente no es posible y es necesario realizar aproximaciones.

• Primeramente observamos que el efecto del campo magnético es mucho más débil que el del campo eléctrico. Por ello, despreciaremos el efecto del magnetismo en esta aproximación. Es evidente que la influencia de los campos magnéticos en, por ejemplo, moléculas magnéticas puede ser muy importante, pero no será algo que trataremos en este curso.

• Seguidamente, notaremos que los campos eléctricos que genera un haz de luz de intensidades típicas en el laboratorio es mucho más débil que los campos generados por núcleos y electrones dentro de la molécula por lo que lo podremos tratar de forma perturbativa. Para ello nuestro hamiltoniano de referencia será el Hamiltoniano molecular, \(h_0\), que ya conocemos, al que le tendremos que añadir la interacción radiación-materia,

(359)\[\hat{h}=\hat{h}_0+\hat{h}_{\text{rad-mat}},\]

donde el hamiltoniano radiación-materia, \(\hat{h}_{\text{rad-mat}}\), es mucho más pequeño que \(\hat{h}_0\).

Antes de discutir con la descripción del Hamiltoniano de interacción radiación materia, se recomienda leer como, cualitativamente, la luz afecta a una molécula, en la caja más abajo, y estudiar que unidades y escalas son típicas en espectroscopia. Aunque breve, esta sección es muy importante.

Ilustración cualitativa del efecto campo eléctrico en molécula

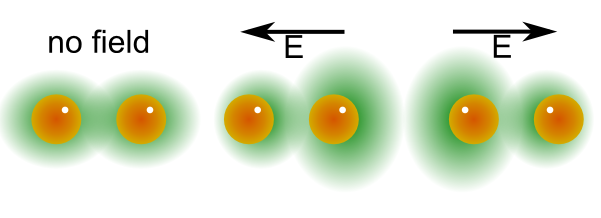
Fig. 224 Una molécula, antes de ser expuesta a radiación, se encuentra en un cierto estado que tiene asociado una distribución de carga determinada, como se muestra en el diagrama superior a la izquierda. Cuando se aplica un campo eléctrico, los electrones (con carga negativa) se moverán en dirección contraria a esta campo mientras que los núcleos lo harán en el mismo sentido del mismo. Dado que la atracción entre núcleos y electrones es mucho más fuerte que el campo aplicado estos movimientos de carga serán pequeños alrededor de la situación sin campo que es podemos considerar de “equilibrio”.

Dado que los campos eléctricos cambian con el tiempo con una frecuencia bien definida, podemos ver ahora los varios regímenes que ocurren, dependiendo de si la frecuencia del campo es menor, igual o menor a las frecuencias típicas de movimiento de los electrones/núcleos. Esta descripción tiene mucho que ver con el movimiento de un oscilador forzado.

Si la frecuencia del campo es pequeña comparada con la de oscilación de la nube electrónica, los electrones observarán un campo que es, aproximadamente, constante. Eso significa que lo seguirán y producirán una polarización que es constante (realmente varía siguiendo al campo), mostrado en la Fig. 225 por un dipolo constante con el tiempo. Este campo no aporta energía a los electrones ya que la amplitud de su oscilación, en promedio, no crece.

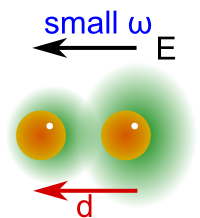
Fig. 225 Cuando la nube electrónica puede adaptarse instantaneamente y seguir al campo, su deformación produce un dipolo que podemos considerar constante para cada valor del campo.

Si la frecuencia del campo ahora es grande con respecto a la de la nube electrónica, los electrones no podrán seguir al campo y se quedarán en su posición inicial. Esto se muestra en la Fig. 226 mediante un dipolo nulo. De nuevo, este campo no aporta energía a los electrones ya que la amplitud de su oscilación no cambiará con el tiempo.

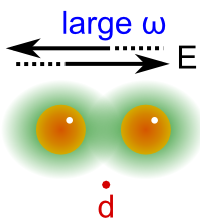
Fig. 226 Cuando la nube electrónica no puede seguir al cambio del campo con el tiempo esencialmente no sufre deformación alguna y se mantiene constante sin formar un dipolo que siga al campo.

Si la frecuencia del campo es la misma a la que la de la nube electrónica puede cambiar de forma, entonces los electrones se moverán acompasadamente con el campo (ver el cambio del dipolo en la Fig. 227), dando lugar al fenómeno de la resonancia. Dado que los electrones van a oscilar cada vez con mayor amplitud, están absorbiendo energía del campo y esto producirá una línea de absorción en el correspondiente espectro.

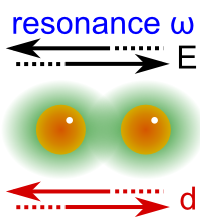
Fig. 227 Cuando el campo cambia con una frecuencia característica del movimiento de los electrones se forma un dipolo oscilante que sigue al campo y crece de amplitud con el tiempo.```

Unidades y escalas en espectroscopia

Tal y como queda claro en la caja anterior la frecuencia de la radiación es muy importante dado que la absorción va a revelar las escalas de los movimientos atómicos.

Lo que llamamos luz tiene que ver con una pequeña parte del espectro, Fig. 228, que es como llamamos el visible. La Fig. 228 muestra como a frecuencias más altas que el visible se encuentran los rangos del ultravioleta, los rayos-X y los rayos gamma, mientras que, para frecuencias menores, encontramos el infrarrojo, las microondas y las ondas de radio.

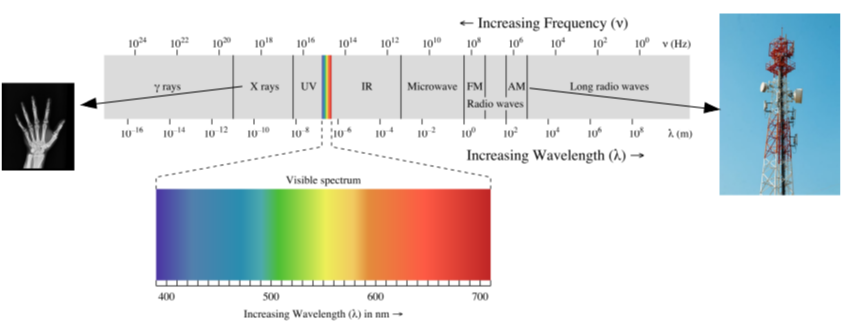
Fig. 228 El espectro electromagnético dividido en los diferentes rangos de frecuencia conocidos como rayos-\(\gamma\), rayos-X, ultravioleta (UV), visible (con sus colores), infrarrojo (IR) y radio. Es importante darse cuenta de la doble escala de frecuencia y longitud de onda con que podemos clasificar estas ondas.

Dependiendo que propiedad queramos observar va a ser importante discutir la frecuencia de la luz (como hemos hecho en la caja Ilustración cualitativa del efecto del campo) pero también puede ser importante la longitud de onda, como veremos en la sección sobre la aproximación dipolar, o su energía. La tabla inferior, Fig. 229, muestra las unidades típicas para diferentes tipos de radiación incluyendo longitud de onda, frecuencia y energía. Una característica de muchas medidas de espectroscopía es dar el módulo del vector de ondas, \(\tilde{k}\), medido en \(cm^{-1}\). Usando la velocidad de la luz podemos mostrar que este valor es proporcional a la energía y por tanto, en ocasiones, se suele intercambiar este valor por una energía de transición (¡aunque, de formar rigurosa, no son exactamente lo mismo!).

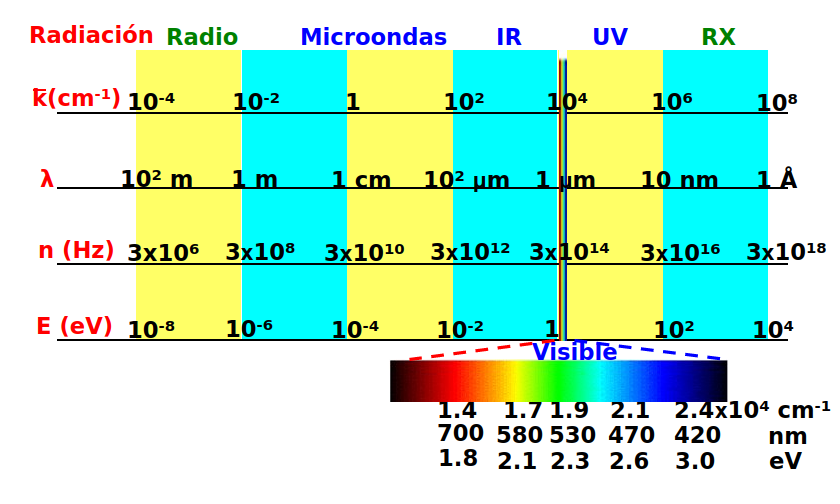
Fig. 229 Tabla en las escalas típicas de medidas espectroscópicas incluyendo el número de ondas (\(\tilde{k}\)), la longitud de onda (\(\lambda\)), la frecuencia (\(\nu\)) y las energías (E), cada una con sus unidades características.

Hamiltoniano de interacción y aproximación dipolar

Para describir el campo electromagnético uno puede usar el campo eléctrico y el magnético o, alternativamente, el potencial escalar, \(v\), y el vectorial, \(\vec{A}\). Cuando un campo electromagnético se aplica a una partícula de carga q, el potencial sobre esa partícula y su momento lineal cuántico cambian de la siguiente manera:

(360)\[v(\vec{r}) \rightarrow v_{\text{inicial}}(\vec{r})+qv_{\text{campo}}(\vec{r})\]

(361)\[\hat{\vec{p}} \rightarrow \hat{\vec{p}} -q \vec{A}\]

Sustituyendo estos valores en el Hamiltoniano molecular podemos obtener el efecto del campo. Aún así, los potenciales (sean escalares o vectores) no están definidos de forma inequívoca y, por tanto, es usual utilizar un gauge, una serie de condiciones extras, que podemos añadir de forma arbitraria para definir de forma completa estos potenciales.

Para el campo electromagnético es usual utilizar el gauge de Coulomb para obtener,

(362)\[\begin{split} \left. \begin{array}{l} \text{Coulomb gauge} \\ \vec{\nabla}\vec{A}=0, v=0 \end{array} \right\}\rightarrow\frac{1}{2m}\left[\vec{p}+e\vec{A}\right]^2= \frac{1}{2m}\vec{p}^2+\frac{e}{2m}\left[\vec{p}\vec{A}+\vec{A}\vec{p}\right]+e^2\vert\vec{A}\vert^2.\end{split}\]

Podemos observar que, con este gauge, el potencial no cambia pero que la energía cinética da lugar a tres términos. El primero es la energía cinética usual de un electrón (\(\vec{p}^2/2m\)). El último es un ´termino que tiene que ver con el cuadrado del potencial vector, \(\vert\vec{A}\vert^2\), y que está relacionado con la energía del campo. Finalmente, tenemos un término cruzado que expresa, precisamente, la interacción campo-materia,

(363)\[h_\text{int}=\frac{e}{2m}\left[\vec{p}\vec{A}+\vec{A}\vec{p}\right],\]

y que nosotros usaremos como perturbación para observar el efecto de la radiación sobre una molécula.

Interacción dipolar

Uno de los problemas que tenemos para resolver el problema de los campos es que una molécula experimenta una intensidad del campo diferente en diferentes puntos (diferentes átomos). Si observamos la longitud de onda de la luz normalmente disponible en un laboratorio (visible, infrarrojo, incluso ultravioleta) podemos observar que sus longitudes de onda van de las varias decenas de nanometros a los milímetros que son, en general, mucho más grandes que una molécula (cuyo tamaño típico puede ser un nanometro).

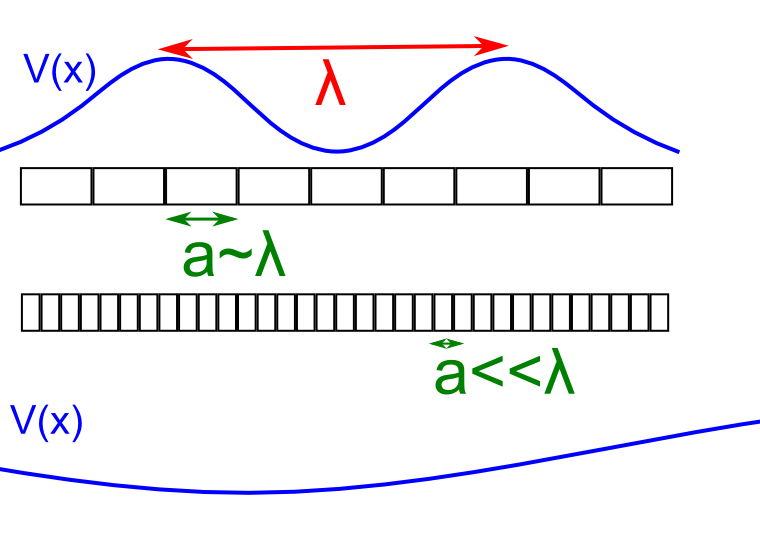
Fig. 230 Comparación entre el tamaño típico de una molécula (\(a\)), que representaremos como una caja en el dibujo, y la longitud de onda de la radiación (\(\lambda\)), representado por una curva oscilante. En el caso superior, el campo varía de forma notable a lo largo de una longitud \(a\). En cambio, en el caso inferior, con una mayor longitud de onda, el campo es prácticamente constante a lo largo de una molécula.

Si intentamos visualizar esta situación, como en la Fig. 230, podemos observar que si la molécula, de longitud \(a\), es mucho más pequeña que la longitud de onda (\(a\ll\lambda\)) el campo observado es, aproximadamente, constante en toda la molécula. Efectivamente, si tomamos el vector potentical y tomamos el vector de ondas como pequeño, \(q=2\pi/\lambda \rightarrow 0\), encontramos,

(364)\[\vec{A}(t,\vec{r})=\vec{A}_0 \left[e^{i\left(\vec{q}\vec{r}-\omega t\right)}-e^{-i\left(\vec{q}\vec{r}-\omega t\right)}\right]\approx \vec{A}_0 \left(e^{-i\omega t}-e^{i\omega t}\right)~~~~q=2\pi/\lambda\]

Si ahora observamos la relación del campo con el potencial vector,

(365)\[\vec{E}(t,\vec{r})=-\vec{\nabla}v-\frac{\partial \vec{A}}{\partial t}\]

podemos notar que, en la aproximación dipolar, el campo eléctrico es sencillamente un campo homogéneo que varía con el tiempo. Es decir, sería equivalente el aplicar un potencial escalar de la forma,

(366)\[\hat{h}_{\text{int}}(t)=e\vec{E}(t)\vec{r}.\]

Intensidad de las transiciones y reglas de selección

Una vez tenemos el Hamiltoniano de interacción bajo la aproximación adiabática, podemos usar teoría de perturbaciones dependiente del tiempo [11] para encontrar la probabilidad de transición de un estado inicial a uno final (equivalente a usar la regla de oro de Fermi) por unidad de tiempo,

(367)\[\mathcal{P}_{i\rightarrow f} = \frac{2\pi}{\hbar}\left\vert \left\langle \psi_i \right\vert \hat{H}_\text{int} \left\vert \psi_f \right\rangle \right\vert^2.\]

Si definimos el elemento de matriz de transición dipolar entre un estado inicial y uno final como el valor esperado del operador de posición,

(368)\[\vec{\mu}_{if}=\left\langle \psi_i \right\vert \vec{r} \left\vert \psi_f \right\rangle\]

tenemos que el valor de la probabilidad de transición, sustituyendo el valor del hamiltoniano de interacción, Ec. (366), es,

(369)\[\mathcal{P}_{i\rightarrow f}=\frac{2\pi}{\hbar}\left\vert \left\langle \psi_i \right\vert -e\vec{E}\cdot\vec{r} \left\vert \psi_f \right\rangle \right\vert^2 = \frac{2\pi e^2}{\hbar}\left\vert \vec{E}\cdot\vec{\mu}_{if} \right\vert^2.\]

Con esto podemos ver que para que exista transición el elemento dipolar de transición entre dos estados tiene que ser no nulo y que la absorción será más fuerte cuanto más grande sea este valor.

Reglas de selección

Desde el punto de vista general podemos estudiar mediante simetría cuando el elemento de matriz \(\vec{\mu}_{if}\) es nulo y cuando no (ver Sec. productos de irrep). Para ello debemos comprobar si el producto de la irrep asociada al estado inicial, la irrep asociada al estado final y la irrep asociada al operador posición, \(\vec{r}\), involucran la irrep totalmente simétrica o no. Si el producto expande la irrep totalmente simétrica el elemento de matriz puede ser no nulo y la transición podrá ser observada. En caso contrario será nulo y la transición no podrá observarse.

Por ejemplo, si el sistema posee simetría de inversión, lo que hace que las irreps puedan ser pares o impares con respecto a la inversión (indicado por un subíndice g (gerade) o u (ungerade) en el símbolo del estado). Además, podemos comprobar como el operador \(\vec{r}\) es siempre impar (cambia de signo al invertirse), por lo que tenemos que,

(370)\[\left\langle \psi_g \right\vert \vec{r} \left\vert \psi_u \right\rangle \neq0; ~~ \left\langle \psi_u \right\vert \vec{r} \left\vert \psi_g \right\rangle \neq 0; ~~ \left\langle \psi_g \right\vert \vec{r} \left\vert \psi_g \right\rangle = \left\langle \psi_u \right\vert \vec{r} \left\vert \psi_u \right\rangle=0\]

es decir, si los estados inicial y final tienen la misma paridad la transición no puede observarse mientras que si tienen paridades opuestas sí se observará.

En funciones de onda vibracionales, si un modo es par (g) todos sus estados (asociados al número cuántico del oscilador \(\nu\)) son pares, mientras que si es impar (u) su estado fundamental y todos los excitados con número cuántico \(\nu\) par son pares, mientras que \(\nu\) impar implica un estado ungerade. Por tanto, un modo caracterizado por ser par (gerade) no podrá observarse mediante espectroscopia, mientras que un modo de tipo ungerade podrá observarse.

Discutamos ahora las reglas de selección para cada tipo de fenómeno asociado al movimiento de los núcleos.

Transiciones rotacionales

El elemento de transición en las rotaciones es,

(371)\[\vec{\mu}_{ij}=\left\langle ev J^\prime M_{J^\prime} \right\vert \vec{\mu} \left\vert ev J M_{J} \right\rangle = \left\langle Y_{J^\prime}^{M_{J^\prime}} \right\vert \vec{\mu}_0 \left\vert Y_J^{M_{J}} \right\rangle\]

donde \(Y_J{M_{J}}\) son las autofunciones del operador momento angular, los armónicos esféricos, y los números cuánticos e y \(\nu\) representan, respectivamente, el estado electrónico fundamental y el estado vibracional. Para que una molécula interaccione con un campo eléctrico y este la haga rotar, la molécula debe de contar con un dipolo eléctrico en su geometría de equilibrio. Este es,

(372)\[\vec{\mu}_0=\left\langle ev \right\vert \vec{\mu} \left\vert ev\right\rangle\]

Es decir, el espectro rotacional (en el estado fundamental) sólo puede observarse en moléculas polares. Si ahora observamos con más detalle el elemento de transición, podemos ver,

(373)\[\begin{split}\left\langle Y_{J^\prime}^{M_{J^\prime}} \right\vert \vec{\mu}_0 \left\vert Y_J^{M_{J}} \right\rangle\neq 0 \rightarrow \vec{\mu}_0\rightarrow \begin{cases} J=1 \\ \text{paridad=-1} \end{cases} \Longrightarrow \Delta J = \pm 1 (+1 ~\text{absorción}, -1 ~\text{emisión})\end{split}\]

es decir, que para que una transición rotacional pueda observarse el número cuántico asociado al módulo del momento angular debe cambiar en 1,

(374)\[\Delta M_J =0, \pm 1.\]

Ejemplo

Supongamos ahora un rotor esférico. En estos sistemas la energía de los niveles rotacionales tan sólo dependía del módulo del momento angular, J,

(375)\[F(J)=B^\prime J(J+1)\]

donde \(B\prime\) es la constante rotacional \(B^\prime=\hbar^2/2I\). Dado que tan sólo podemos observar transiciones entre dos niveles cuyo número del momento angular difiere en 1 tenemos las energías de transición,

(376)\[J\rightarrow J+1: F(J+1)-F(J)=2B^\prime \left(J+1\right),\]

es decir, la energía observada depende del estado J del que parta la transición.

En el caso de las energías rotacionales los niveles están separados, tan sólo por algunas milésimas de eV. Eso significa que, dado que la población térmica de los niveles tiene que ver con la constante de Boltzmann (\(k_B=8.6\cdot 10^{-5} eV/K\)), a temperaturas usuales, \(T\approx 300K\) la energía térmica, \(k_B T \approx 20 meV\), permite poblar varios niveles excitados rotacionales. En particular, la población de los niveles será,

(377)\[P_i = \frac{N_i}{N} = \frac{d_i}{Z} e^{-E_i/KT}\]

donde la función de partición, \(Z\), es,

(378)\[Z = \sum_i d_i e^{-E_i/KT}.\]

Cuando calculamos la probabilidad de ocupación con la energía de los niveles rotaciones (J), obtenemos,

(379)\[P_{J}=(2J+1)e^{-\frac{hcB'J(J+1)}{kT}}\]

donde hemos tenido en cuenta que, aunque la energía tan sólo depende de J, para cada valor de J hay 2J+1 estados degenerados con la misma energía. La Ec. (379) es una función complicada pero que, claramente, posee un máximo. Este lo podemos calcular derivando con respecto a J,

(380)\[\frac{dP_J}{dJ}=0 \rightarrow J_{\text{max}}=\left(\frac{kT}{2hcB^\prime}\right)^{1/2}-\frac{1}{2}\]

Es decir, que para el valor de \(J_{\text{max}}\) esperamos encontrar un máximo en la intensidad de las transiciones rotacionales. Esto es de este modo dado que, si vemos la dependencia de la probabilidad de transición con J,

(381)\[\vert\vec{\mu}_{J,J+1}\vert^2=\vert\vec{\mu}_{0}\vert^2 \frac{J+1}{2J+1} \rightarrow \frac{\vert\vec{\mu}_{0}\vert^2}{2}~~ \text{para}~~ J\gg1\]

esta probabilidad es, aproximadamente, constante.

Efectivamente, cuando observamos un espectro rotacional, como el mostrado en la Fig. 231 observamos un número de líneas igualmente espaciadas (ver Ec. (376)) y cuya probabilidad de absorción crece hasta llegar a un máximo y luego vuelve a descender, como marca la Ec. (380).

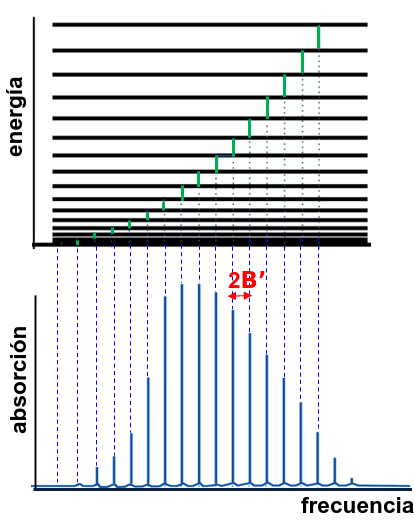
Fig. 231 Figura que muestra, en la parte inferior un espectro rotacional donde las lineas están separadas por el parámetro 2B. En la parte superior se muestran los niveles rotacionales y como la separación entre niveles crece linealmente. El máximo que se observa en el espectro se debe a la población que tienen los niveles rotacionales excitados a temperatura no nula.

Transiciones vibracionales

En una transición vibracional entre el estado \(A_a\) (inicial) y \(B_b\) (final) el elemento de matriz,

(382)\[\vec{\mu}_{ij}=\left\langle A_{\nu_a} \right\vert \vec{r} \left\vert B_{\nu_b} \right\rangle\]

debe ser no nulo. Observando la forma de las funciones del oscilador armónico, Ec. (341), podemos ver que este elemento puede ser no nulo tan sólo cuando el cambio en el número cuántico del oscilador, \(\nu_a \rightarrow \nu_b\) tan sólo cambia en una unidad,

(383)\[\Delta \nu = \pm 1.\]

Dado que la separación entre niveles vibracionales es, en la aproximación armónica, constante eso significa que tan sólo se podría observar una línea, a frecuencia \(\hbar \omega\), para modos impares y que no cambiaría con la temperatura. Si observamos el espectro experimental mostrado en la Fig. 232, podemos ver dos líneas de absorción. La más baja es el modo impar \(\pi_u\) asociado al doblado de la molécula, mientras que la que está a más alta energía es la correspondiente al modo de estiramiento \(\sigma_u\) que, necesariamente, es también de tipo \(u\).

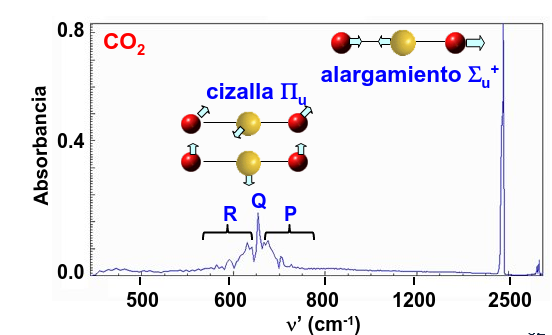
Fig. 232 Espectro infrarrojo del CO\(_2\) donde pueden observarse dos modos activos de absorción. Ambos tienen simetría impar (u), el primero, más ancho, pertence a la irrep \(\pi_u\) y es de cizalla, teniendo una frecuencia más baja que el modo de alargamiento, \(\sigma_u^+\).

Problems and solution examples