Familia de planos

Acabaremos esta lección volviendo a la descripción de los planos cristalinos, es decir, planos que contengan 3 puntos no colineales de la red. Estos serán muy importantes en el siguiente tema para poder entender la difracción de rayos-X en cristales.

En la Fig. 84 representamos varias familias de planos asociadas a una red rectangular sencilla. Como puede observarse, cada familia está definida por un número infinito de planos paralelos que están separados por una distancia interplanar, d, constante.

Fig. 84 Familias de planos (identificadas con un color) asociadas a una red rectangular sencilla con periodicidad bidimensional.

El principal trabajo de esta sección será, precisamente, encontrar la dirección de las familias de planos y la distancia interplanar en las mismas.

Índices de Miller

Vamos a identificar a las familias de planos mediante los llamados índices de Miller que son 3 enteros (h,k,l) que no contienen factores comunes. Estos índices son tales que el primer plano de la familia corta a los 3 ejes convencionales en las coordenadas u (\(\vec{a}\)), v (\(\vec{b}\)) y w (\(\vec{c}\)) de modo que:

(85)\[u=\frac{1}{h} ~~~~~ v=\frac{1}{k} ~~~~~ w=\frac{1}{l}\]

Seguidamente veremos que la dirección de la familia de planos que cumple lo anterior es:

(86)\[\vec{g}_{hkl}=h\vec{a}^\star+k\vec{b}^\star+l\vec{c}^\star\]

Para ello nos fijamos en el diagrama Fig. 85, donde se identifica los vectores de posición contenidos en el primer plano después del origen con el vector \(\vec{R}_1\).

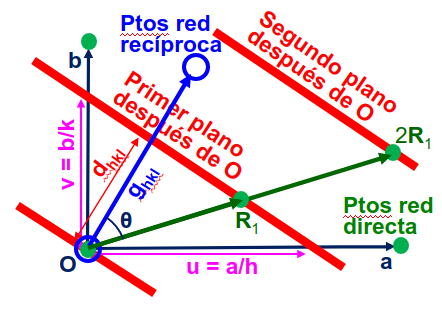
Fig. 85 Ilustración de la definción de los índices de Miller y el cálculo de la distancia interplanar. En el diagrama se muestran los puntos de la red directa (puntos verdes), de la recíproca (puntos azules) y los planos de red (línea rojas). Los índices de Miller tienen que ver con la coordenada fraccionaria en la que el primer plano (después del que pasa por el origen) corta a los ejes convencionales del cristal en los puntos \(u\vec{a}\) y \(v\vec{b}\) (en un sistema tridimensional habría que añadir el tercer eje y su corte en \(w\vec{c}\)).

Recordando que la ecuación de un plano puede escribirse del siguiente modo:

(87)\[\vec{n}\cdot\vec{R}=A\]

donde \(\vec{n}\) es un vector normal al plano y A un número real que determina lo lejos del origen que está el plano (A=0 hace pasar el plano por el origen).

Multiplicando ahora el vector \(\vec{g}_{hkl}\) por \(\vec{R}_1\), y evaluando el resultado para cada uno de los ejes, vemos que los cortes (u,v,w) verifican la definición de los índices de Miller,

(88)\[\begin{split}\vec{g}_{hkl}\cdot \vec{R}_1 = 2\pi N ~ (N=1) \begin{cases} \vec{g}_{hkl} \cdot u\vec{a} = 2\pi \rightarrow hu 2\pi = 2\pi \rightarrow u=\frac{1}{h}\\ \vec{g}_{hkl} \cdot v\vec{b} = 2\pi \rightarrow kv 2\pi = 2\pi \rightarrow v=\frac{1}{k}\\ \vec{g}_{hkl} \cdot w\vec{c} = 2\pi \rightarrow lw 2\pi = 2\pi \rightarrow w=\frac{1}{l} \end{cases} \end{split}\]

Por tanto, a partir de este momento, utilizaremos los vectores \(\vec{g}_{hkl}\)/los índices de Miller (h,k,l) para caracterizar la dirección de los planos.

Ejemplo

Es importante ser capaz de identificar los planos de red con sus índices de Miller. Seguidamente se representan una serie de planos y, en base a donde cortan los ejes de la red convencional, se puede deducir us índices de Miller usando la regla índicada en la Ec. (85).

Fig. 86 Plano (1,0,0)

Fig. 87 Plano (1,1,0)

Fig. 88 Plano (1,1,1)

Fig. 89 Plano (0,2,0)

¡Cuidado!

Es importante darse cuenta que en las celdas I o F el primer plano en la dirección x (o y o z) no es el (1,0,0) si no que, dado que hay puntos de red a media celda convencional, el primero es el (2,0,0) o equivalentes.

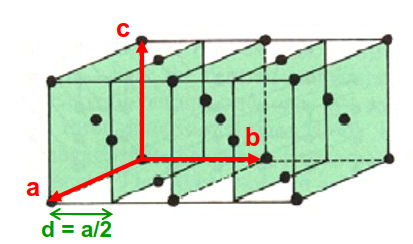
Fig. 90 Los primeros planos en cúbica F no son (0,1,0) si no que el (0,2,0) es el más cercano al origen.

Distancias entre planos

Siguiendo la Fig. 85 y la ecuación (88) vemos que el primer plano de la familia verifica,

(89)\[\vec{g}_{hkl}\cdot \vec{r} = 2\pi\]

Ahora se utilizará que \(\vec{g}_{hkl}\) es un vector perpendicular a la familia de planos y que, por tanto, la distancia entre ellos se mide a lo largo de la línea que marca este vector. En la ecuación anterior el producto \(\vec{g}_{hkl}\cdot\vec{r}\) precisamente tiene que ver con la proyección de \(\vec{r}\) a lo largo de la línea perpendicular al plano. Desarrollando el producto escalar tenemos que,

(90)\[\vec{g}_{hkl}\cdot \vec{r} = g_{hkl} r\cos\theta\]

donde \(r\cos\theta\) es precisamente la distancia entre planos (ver Fig. 85), por lo que,

(91)\[\vec{g}_{hkl}\cdot \vec{r} = \vert \vec{g}_{hkl}\vert r\cos\theta=g_{hkl} d_{hkl} =2\pi\]

Por tanto, la distancia interplanar tiene una relación sencilla con el módulo del vector \(\vec{g}_{hkl}\),

(92)\[d_{hkl}=\frac{2\pi}{\vert \vec{g}_{hkl}\vert} = \frac{2\pi}{g_{hkl}} \]

Fig. 91 Ilustración del vector \(\vec{g}_{hkl}\) y su relación con la distancia interplanar.

De forma práctica es mejor usar la inversa del cuadrado de la última expresión para encontrar la distancia interplanar.

(93)\[\frac{1}{d_{hkl}^2}=\frac{\left(h\vec{a}^\star+k\vec{b}^\star+l\vec{c}^\star\right)^2}{4\pi^2}\]

Ejemplo

Tomando los vectores de una red recíproca cúbica,

\[\vec{a}^\star=\frac{2\pi}{a} ~~~~~ \vec{c}^\star=\frac{2\pi}{a} ~~~~~ \vec{c}^\star=\frac{2\pi}{a} \]

y usando la Ec. (93) para encontrar las distancias interplanares tenemos que,

(94)\[\frac{1}{d_{hkl}^2}=\frac{h^2+k^2+l^2}{a^2} \]

Problemas y ejemplos