Reglas de selección

Hasta el momento se ha tratado la ley de Bragg que nos indica los ángulos para los que esperamos observar un pico en el diagrama de difracción de rayos-X. En esta sección discutiremos la altura (intensidad) que tendrán cada uno de estos picos. Observaremos que hay líneas que, sistemáticamente, van a tener intensidad nula (extinciones) y que por tanto no podrán observarse. Podremos predecir estas líneas mediante las regla de selección.

Intensidad en un diagrama de rayos-X

Como explicábamos en la introducción, la interacción de un rayo-X con la materia excita un electrón cercano al núcleo y, cuando este se desexcita, reemite un rayo-X de la misma energía. Es por ello claro que la intensidad de un diagrama de rayos-X tiene que incrementarse con la densidad de electrones, que es más alta cuanto más cerca del núcleo nos encontremos (ver, por ejemplo, las funciones radiales de probabilidad del átomo de hidrógeno).

En particular, la intensidad de un diagrama de rayos-X es proporcional al factor de forma atómico, que es la transformada de Fourier de la densidad electrónica,

(106)\[I(\vec{q})\propto \vert F(\vec{q})\vert^2 \rightarrow F(\vec{q})=\int n(\vec{r}) e^{i\vec{q}\vec{r}}d^3r \approx F_\text{red} F_\text{motivo}.\]

A su vez vamos a dividir, de forma aproximada, el factor de forma en una parte que depende de la red,

(107)\[F_\text{red}=\sum_{\vec{R}} e^{-i \vec{q}\vec{R}} \]

y otra parte que depende del motivo,

(108)\[ F_\text{motivo}=\sum_{\alpha} f_\alpha (\vec{q}) e^{-i \vec{q}\vec{r}_\alpha}.\]

En el caso de la regla de selección, de la red el sumatorio se extiende a todos los puntos de red primitivos que están dentro de la red convencional del sistema. En el caso del motivo, el sumatorio se extiende a todos los átomos que lo forman.

Por tanto, podemos ver que hay dos casos en los que habrá reglas de selección para diagramas de rayos-X:

-1: Redes en las que la celda convencional no sea la primitiva (I, F, A, B, C).

-2: Motivos en las que los átomos formen patrones con operaciones de simetría compuestas (como ejes helicoidales o planos de deslizamiento)

Reglas de selección de redes cúbicas

Trabajemos, como ejemplo, las reglas de selección asociadas a las redes cúbicas. Para ello aplicaremos la Ec. (107) para los casos de redes P, I y F.

Cúbica P

En el caso de una red cúbica P (Fig. 100) tenemos un único punto de red con coordenadas,

(109)\[\vec{R}_1=[000]\]

Sustituyendo en Ec. (107) se obtiene,

(110)\[F_\text{red}=\sum_{\vec{R}} e^{-i\vec{q}\cdot\vec{R}} = e^0 = 1\]

Dado que \(F_\text{red}\) no puede ser nulo no hay reglas de selección de red para los cristales cúbicos P.

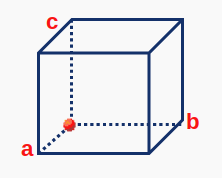
Fig. 100 Diagrama para red cúbica P mostrando con un punto rojo el único punto de red en su interior.

Cúbica I

En el caso de una red cúbica I (Fig. 101) tenemos dos puntos de red dentro de la celda convencional. Tienen coordenadas,

(111)\[\vec{R}_1=[000], \vec{R}_2=[\tfrac{1}{2} \tfrac{1}{2} \tfrac{1}{2}]\]

Construyendo, ahora, el factor de forma de red, se obtiene,

(112)\[\begin{split} F_\text{red}=\sum_{\vec{R}} e^{-i\vec{q}\cdot\vec{R}} = 1+ e^{-i\pi(h+k+l)} = \begin{cases} 1+1 =2 ~ \text{si} ~ h+k+l=\text{par} \\ 1-1 =0 ~ \text{si} ~ h+k+l=\text{impar} \end{cases}\end{split}\]

donde podemos observar que se anula si la suma de los índices de Miller de una línea es un número impar.

Fig. 101 Diagrama para red cúbica I mostrando con puntos rojos los dos puntos de red (primitiva) en su interior.

Cúbica F

Finalmente, en el caso de una red cúbica F (Fig. 102) hay cuatro puntos de red dentro de la celda convencional. Sus coordenadas son,

(113)\[\vec{R}_1=[000], \vec{R}_2=[0 \tfrac{1}{2} \tfrac{1}{2}], \vec{R}_3=[\tfrac{1}{2} 0 \tfrac{1}{2}], \vec{R}_4=[\tfrac{1}{2} 0 \tfrac{1}{2}]\]

Usando estas coordenadas y la Ec. (107) se llega a,

(114)\[\begin{split} F_\text{red}&=\sum_{\vec{R}} e^{-i\vec{q}\cdot\vec{R}} = 1+ e^{-i\pi(h+k)}+ e^{-i\pi(h+l)+ e^{-i\pi(l+k)}} \\& = \begin{cases} 4 ~ \text{si} ~ h,k,l ~ \text{misma paridad} \\ 0 ~ \text{si} ~ h,k,l=\text{otro caso} \end{cases}\end{split}\]

En este caso se obtiene que las líneas tan sólo pueden observarse si h, k y l tienen la misma paridad, es decir, son todos pares o todos impares.

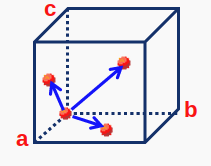
Fig. 102 Diagrama para red cúbica F donde se muestran con puntos rojos los 4 puntos de red contenidos en el interior de la red convencional.

Problemas y ejemplos