Simetría#
Observando la estructura de muchas moléculas y sólidos (ver Fig. 116) se puede notar que su geometría está marcada por la simetría, es decir, podemos girarla o voltearlas y encontramos siempre la misma forma.

Fig. 116 Representación gráfica de varias moléculas sencillas de gran importancia al igual que la estructura de un śolido iónico (cloruro sódico) y otro covalente (silicio). Puede observarse que muchas tienen formas geométricas regulares, como una pirámide regular (amoníaco), un hexágono (benceno), rectangular (etileno) o las estructuras cúbicas de la sal cómun, con coordinación octaédrica, y del silicio, con coordinación tetraédrica.#
La idea de simetría suele venir asociada a la de belleza estética (ver Fig. 117) y muchas obras de arte la usan para cobrar fuerza. En la naturaleza también se da en los seres vivos, donde muchas estructuras que son simétricas. Lo podemos interpretar como una manera de repetir algo que es igual pero de forma ligeramente diferente, lo cual tiene muchos usos prácticos.

Fig. 117 Los seres vivos, como la mariposa mostrada a la izquierda, o el fractal mostrado a la derecha presentan simetría. La simetría, en muchos casos, apela a nuestro sentido estético. (Figura derecha (C) Ph. Wautelet (www.fractalzone.be))#
Desde el punto de vista cuántico uno podría pensar que algo que es simétrico, como el fractal de la Fig. 117 requiere menos esfuerzo para ser descrito ya que, por ejemplo, podríamos dar información tan sólo de uno de los “pétalos” de la estructura y el resto sería equivalente. A este nivel la simetría tan sólo sería un recurso para reducir nuestro trabajo pero, como veremos en este capítulo, entender la mecánica cuántica es realmente difícil sin el uso de la simetría.
¿Cómo caracterizamos a los estados cuánticos?#
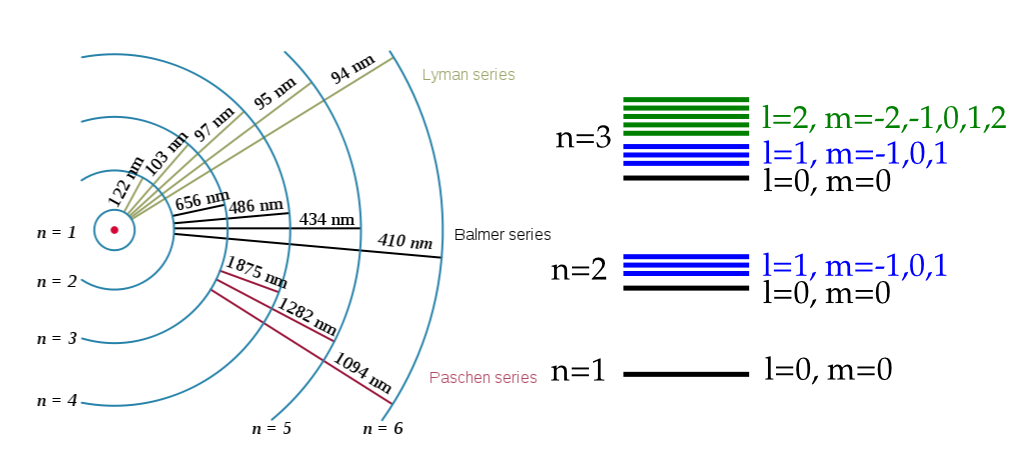
Fig. 118 Niveles del átomo de hidrógeno con líneas representando las diferentes series espectroscópicas que permiten observar la diferencia de energía entre las mismas. En la derecha se muestra un esquema d elos niveles y sus números cuánticos. (C) Wikipedia)#
En la Fig. 118 se muestra un esquema del átomo de hidrógeno y las transiciones posibles entre sus niveles. Estos datos fueron clave para poder establecer la teoría cuántica y el cálculo de estos niveles son uno de sus principales resultados. Una de las preguntas que se podría hacer a cualquier estudiante de física cuántica es, ¿cómo caracterizamos los niveles cuánticos? y una respuesta razonable sería que dando sus números cuánticos (mostrados en la parte derecha de la figura).
Otra pregunta, que probablemente fuera más difícil de responder, es como se consiguen estos número cuánticos y la respuesta usual podría que ser que resolviendo la compleja ecuación diferencial que es la ecuación de Schrödinger. Esta última respuesta no es muy satisfactoria ya que significa que sólo podemos encontrar los números cuánticos de sistemas en los que sabemos resolver la ecuación de Schrödinger y esos no son muchos.
Una respuesta de la que podemos extraer más información sería indicar que, en mecánica cuántica, para definir un estado necesitamos dar un conjunto completo de operadores que conmutan,
Lo que no está tan claro es como escoger estos operadores de forma sistemática. En este tema intentaremos dar respuesta a esta pregunta a la vez que usamos la simetría para ayudarnos a resolver la ecuación de Schrödinger.
