Moléculas diatómicas homonucleares

En esta sección extenderemos los discutido para las moléculas de hidrógeno y helio al segundo periodo de la tabla periódica donde se sitúan los átomos de litio, berilio, boro, carbono, nitrógeno, oxígeno, flúor y neón. El procedimiento será muy similar al de las moléculas anteriores pero habrá dos importantes diferencias:

• En estos átomos, donde llenamos la capa atómica con número cuántico principal n=2 hay orbitales muy internos (la capa n=1) y veremos que efecto tiene su presencia.

• En estos átomos es necesario tratar con orbitales de tipo 2s, que llenan el litio y el berilio, pero también con orbitales 2p, que son muy importantes en el resto de las moléculas de la serie.

Después de discutir estos dos puntos centrales analizaremos el efecto de poblar los diferentes niveles y definiremos el orden de enlace. Acabaremos la sección analizando algunas moléculas particulares y la evolución de los niveles a lo largo del periodo.

Efecto de los orbitales internos (de core)

Los orbitales atómicos normalmente se dividen en orbitales de valencia (la última capa que está llenando el átomo) e internos, también conocidos por el anglicismo de core, que pertenecen a capas completamente llenas y con un valor del número cuántico principal, n, inferior al de la última capa.

Desde el punto de vista de formar enlaces es importante tener en cuenta que los orbitales deben tener una extensión espacial similar a la distancia de enlace para que la integral de solape, clave en las discusiones anteriores, sea grande. Si observamos la parte radial de los orbitales hidrogenoides,

(279)\[R_{nl}(r)=C\left(\frac{2Zr}{na_0^\star}\right)^l L_{n-l-1}^{(2l+1)}\left(\frac{2Zr}{na_0^\star}\right) e^{-Zr/na_0^\star}\]

donde \(L_{n-l-1}^{(2l+1))}\) son los polinomios de Laguerre generalizados, \(a_0^\star=4\pi\varepsilon_0 \hbar^2/\mu e^2\) es el radio de Bohr reducido y Z es la carga del núcleo.

En esta expresión es claro que un aumento de la carga nuclear o una disminución del número cuántico principal producen una compresión del orbital, lo que reducirá la habilidad de este orbital atómico para contribuir al enlace químico.

Es claro que la capa de valencia tiene el mayor valor de \(n\) posible, por lo que sus orbitales tienden a ser más expandidos que los de cualquier capa interior. Por otro lado, la carga efectiva que experimentan los electrones en un átomo multielectrónico depende de la capa en la que estén. En la capa \(n=1\) los electrones observan la carga nuclear total, Z. En cambio, los electrones de la capa \(n=2\) están a una distancia promedio superior que los de la capa \(n=1\) por lo que la carga nuclear efectiva que observan es aproximadamente \(Z^*\approx Z-2\), donde 2 son los electrones de la capa \(n=1\), etc. Es decir, cuanto más nos acerquemos a la capa de valencia en un átomo multielectrónico menor será la carga efectiva que debemos usar en los orbitales atómicos y más extendidos serán estos últimos. Por el contrario, cuanto más profundo sea el orbital más localizado estará y menos participará en el enlace.

Como resultado de esta discusión podemos ver que los orbitales internos son muy compactos, no se ven muy afectados por otros átomos cerca del átomo al que pertenecen y su participación en el enlace es, en general, muy pequeña y podemos no tenerlos en cuenta.

Orbitales 2p

En el segundo periodo de la tabla periódica los átomos empiezan a llenar los orbitales p, empezando por el boro, cuya configuración electrónica es \((1s)^2(2s)^2(2p)^1\). Tal y como explicamos en la sección sobre las LCAO utilizaremos orbitales p reales, como los que están ilustrados en la Fig. 161.

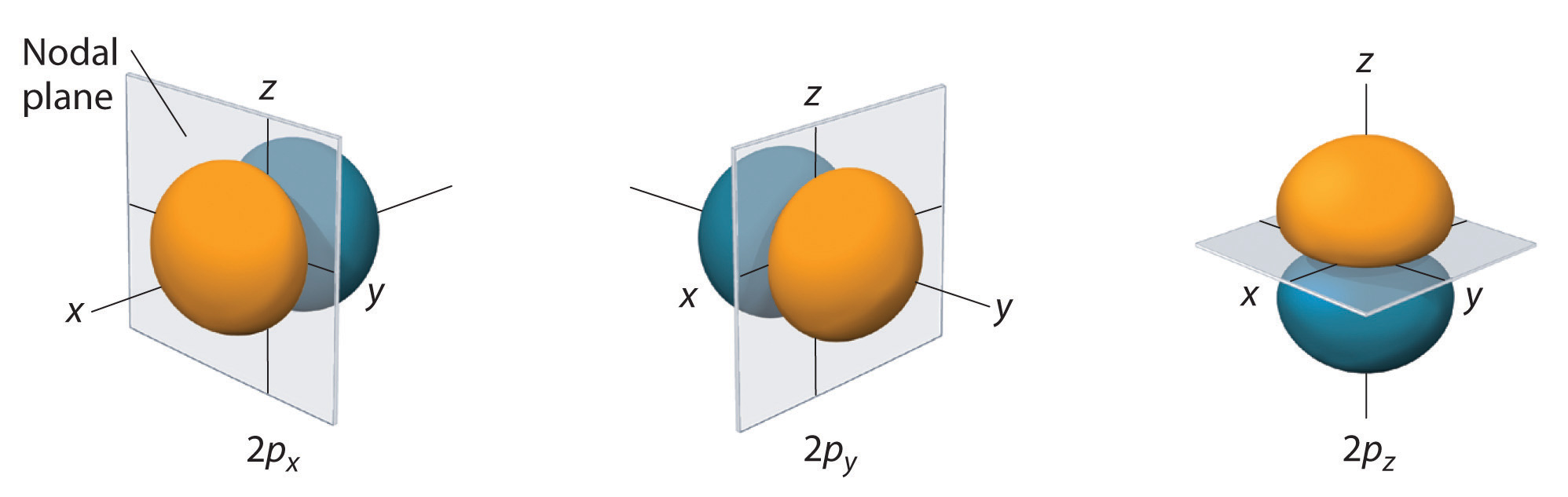
Fig. 161 Tres orbitales 2p reales, \(p_x\), \(p_y\) y \(p_z\). El color naranja indica fase positiva y la azul fase negativa. Estas fases serán muy importantes cuando se discuta los efectos de interferencia entre los orbitales atómicos en un enlace.

Interacciones entre orbitales 2p

Como indicábamos en el ion \(H_2^+\) las integrales hamiltonianas entre diferentes orbitales atómicos, \(h_{ab}\), eran fuertemente dependientes del solape. En particular, dado que el hamiltoniano pertenece a la irrep totalmente simétrica es fácil comprender que la integral \(\left\langle \chi_a \right\vert \hat{h} \left\vert \chi_b \right\rangle\) se anula siempre que el solape \(\left\langle \chi_a \right\vert \left. \chi_b \right\rangle\) lo haga también. Por tanto, para comprender cualitativamente como de fuerte son las interacciones entre diferentes orbitales 2p debemos entender cuando el solape entre estas funciones se anula o es grande.

Primero observaremos que los orbitales intraatómicos (dentro del mismo átomo) son ortogonales entre sí, por lo que el elemento de matriz entre orbitales del mismo átomo lo tomaremos como cero. Esto realmente no exacto debido a que puede haber campos eléctricos que mezclen estos orbitales entre sí o interacciones electrón-electrón entre estos orbitales. En cualquier caso las interacciones intraatómicas no son piezas fundamentales para entender las bases físicas del enlace (aunque pueden ser importantes en otros problemas más delicados) y, sabiendo que es una aproximación grosera, las despreciaremos en este curso.

Supongamos ahora una molécula diatómica \(X_2\) donde el eje que une los dos átomos es el eje principal (eje z). En ese caso los orbitales \(2p_z\) estarán alineados con el eje mientras que \(2p_x\) o \(2p_y\) serán perpendiculares al mismo. Viendo la Fig. 165 es fácil comprobar que la integral de \(2p_z\) en un átomo con un \(2p_x\) (o \(2p_y\)) en el otro es nula.

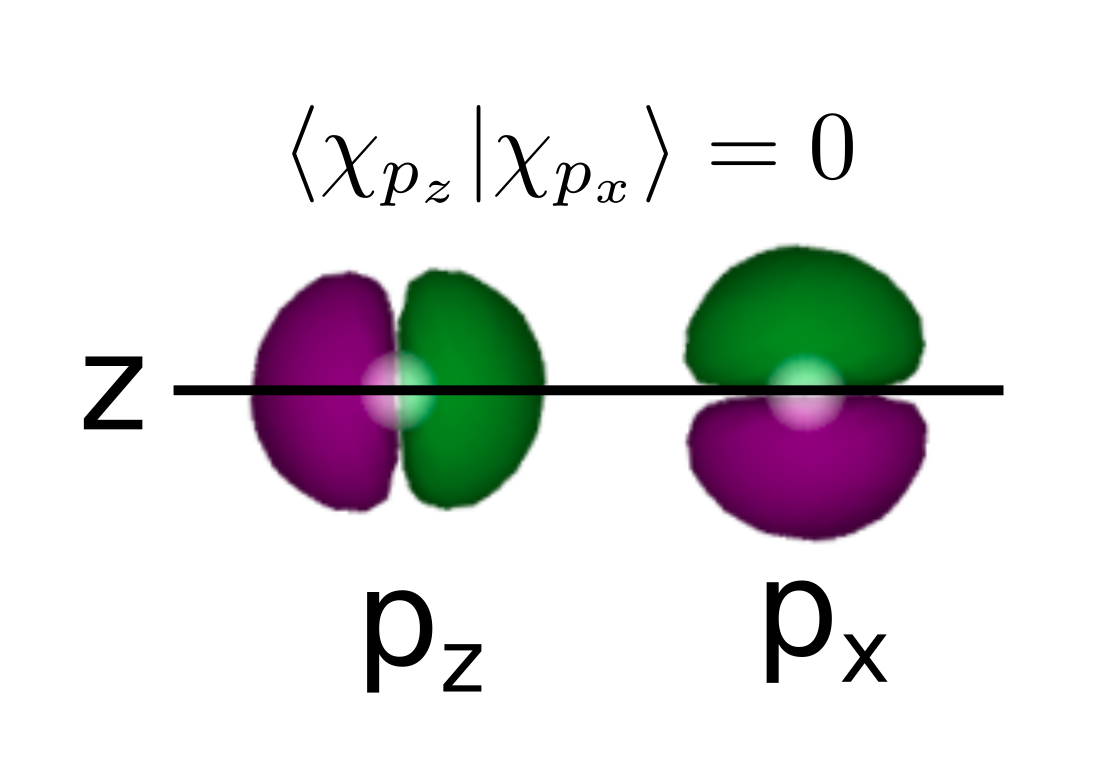
Fig. 162 El solape entre orbitales perpendiculares es nulo. Podemos comprobar que el integrando en la parte superior de la figura es positivo (la fase positiva se muestra verde y la negativa morada) dado a que debemos multiplicar la fase del lóbulo de la función \(2p_z\) más cercana al orbital \(2p_x\) (verde) por el lóbulo superior de \(2p_x\) (positivo también). En cambio en la parte inferior debemos multiplicar la fase positiva del orbital \(2p_z\) por la fase negativa del \(2p_x\). Por tanto, la parte superior e inferior de la figura dan lugar al mismo integrando pero con signos diferentes. Cuando sumemos a todo el espacio la integral se compensará y el resultado total será 0.

Por otro lado, si consideramos la interacción entre los orbitales \(2p_z\) de cada átomo (ver Fig. 163) tenemos, trivialmente, que el solape es no nulo. Por otro lado si consideramos las interacciones entre los orbitales \(2p_x\) en cada átomo entre ellos (o de los \(2p_y\) entre sí) observamos que el solape tampoco es nulo (ver Fig. 164). Es decir, que los orbitales \(2p_x\), \(2p_y\) y \(2p_z\) interaccionan por parejas (x con x, y con y, z con z). Numéricamente, el solape entre los orbitales \(2p_z\) es mucho mayor que el que se corresponde con los orbitales \(2p_x\) y \(2p_y\), que es igual entre sí (estos orbitales son equivalentes) dado que los orbitales \(p_z\) están dirigidos espacialmente el uno contra el otro.

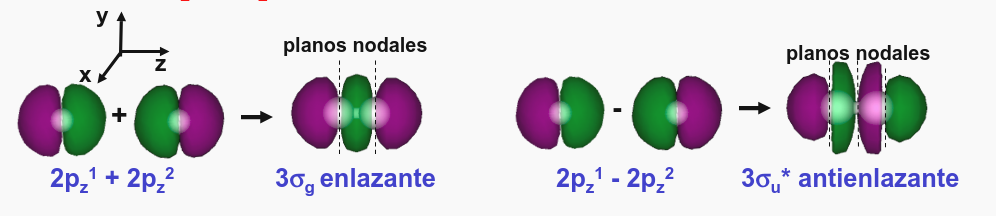
Fig. 163 Ilustración de la interacción de los orbitales \(2p_z\) entre sí en una molécula diatómica homonuclear. El solape entre los orbitales es no nulo y la combinación de ambos orbitales atómicos da lugar a un orbital \(\sigma\) enlazante y otro antienlazante. Nótese que los orbitales están dirigidos el uno contra el otro lo que hace que el valor absoluto del solape sea mayor que en el caso de los orbitales \(\pi\) (Fig. 164).

Fig. 164 Ilustración de la interacción de los orbitales \(2p_y\) entre sí en una molécula diatómica homonuclear (\(2p_x\) sería totalmente equivalente). El solape entre los orbitales es no nulo y la combinación de ambos orbitales atómicos da lugar a un orbital \(\sigma\) enlazante y otro antienlazante. Nótese que los orbitales se colocan en paralelo uno al otro lo que hace que el valor absoluto del solape sea menor que en el caso de los orbitales \(\sigma\) (Fig. 163).

Una vez que hemos estudiado el solape entre orbitales estamos en situación de construir un modelo sencillo de matriz hamiltoniana. El método que vamos a seguir es similar al método de Hückel o a un modelo de enlace-fuerte (también conocido por tight-binding) sencillo. Los elementos diagonales se corresponden con el valor esperado del Hamiltoniano con los orbitales 2p en cada átomo. Aunque es claro que el elemento de \(2p_z\) será algo diferente del \(2p_x\) (que es igual al \(2p_y\)) ya que está dirigido hacia el otro núcleo, aquí aproximaremos todos estos elementos por el mismo valor:

(280)\[\varepsilon_{2p}=\left\langle \chi_{2p_z}^{(i)}\right\vert \hat{h} \left\vert \chi_{2p_z}^{(i)}\right\rangle\]

En la expresión anterior el superíndice \((i)\) indica el átomo al que pertenece el orbital, en este caso el mismo. Cuando calculamos los elementos no diagonales, \(h_{ab}\), indicaremos que son proporcionales a la integral de solape (ver el cálculo del ion \(H_2^+\)) y por tanto, tendremos un elemento hamiltoniano entre orbitales \(2p_z\),

(281)\[\gamma_{\sigma}=\left\langle \chi_{2p_z}^{(1)}\right\vert \hat{h} \left\vert \chi_{2p_z}^{(2)}\right\rangle=\left\langle \chi_{2p_z}^{(2)}\right\vert \hat{h} \left\vert \chi_{2p_z}^{(1)}\right\rangle\]

donde el elemento y su complejo conjugado son iguales dado que los orbitales son reales. Por otro lado para los orbitales \(2p_x\) y \(2p_y\) tendremos,

(282)\[\gamma_{\pi}=\left\langle \chi_{2p_x}^{(1)}\right\vert \hat{h} \left\vert \chi_{2p_x}^{(2)}\right\rangle=\left\langle \chi_{2p_x}^{(2)}\right\vert \hat{h} \left\vert \chi_{2p_x}^{(1)}\right\rangle=\left\langle \chi_{2p_y}^{(1)}\right\vert \hat{h} \left\vert \chi_{2p_y}^{(2)}\right\rangle=\left\langle \chi_{2p_y}^{(2)}\right\vert \hat{h} \left\vert \chi_{2p_y}^{(1)}\right\rangle\]

Con lo que la matriz hamiltoniana en la base \([2p_x^{(1)},2p_y^{(1)},2p_z^{(1)},2p_x^{(2)},2p_y^{(2)},2p_z^{(2)}]\) es,

(283)\[\begin{split}h=\begin{pmatrix} \varepsilon_p & 0 & 0 & \gamma_\pi & 0 & 0\\ 0 &\varepsilon_p & 0 & 0 & \gamma_\pi & 0 \\ 0 & 0 & \varepsilon_p & 0 & 0 & \gamma_\sigma\\ \gamma_\pi & 0 & 0 &\varepsilon_p & 0 & 0 \\ 0 & \gamma_\pi & 0 & 0 &\varepsilon_p & 0 \\ 0 & 0 & \gamma_\sigma & 0 & 0 &\varepsilon_p \end{pmatrix}\end{split}\]

Reordenando la base a \([2p_x^{(1)},2p_x^{(2)},2p_y^{(1)},2p_y^{(2)},2p_z^{(1)},2p_z^{(2)}]\) podemos ver que tenemos un Hamiltoniano por cajas,

(284)\[\begin{split}h=\begin{pmatrix} \varepsilon_p & \gamma_\pi & 0 & 0 & 0 & 0\\ \gamma_\pi &\varepsilon_p & 0 & 0 & 0 & 0 \\ 0 & 0 & \varepsilon_p & \gamma_\pi & 0 & 0\\ 0 & 0 & \gamma_\pi &\varepsilon_p & 0 & 0 \\ 0 & 0 & 0 & 0 &\varepsilon_p & \gamma_\sigma \\ 0 & 0 & 0 & 0 & \gamma_\sigma &\varepsilon_p \end{pmatrix}\end{split}\]

que es muy sencillo de diagonalizar en cada una de las cajas 2x2. Los autovalores son:

(285)\[\begin{split}\varepsilon_\pi=\varepsilon_p\pm \gamma_\pi\\ \varepsilon_\sigma=\varepsilon_p\pm \gamma_\sigma \end{split}\]

y los autovectores son,

(286)\[\begin{split}\psi_{\pi\pm}^{(x)}=\frac{1}{\sqrt{2}} \left( \chi_{2p_x}^{(1)} \pm \chi_{2p_x}^{(2)}\right) \\ \psi_{\pi\pm}^{(y)}=\frac{1}{\sqrt{2}} \left( \chi_{2p_y}^{(1)} \pm \chi_{2p_y}^{(2)}\right) \\ \psi_{\sigma\pm}^{(x)}=\frac{1}{\sqrt{2}} \left( \chi_{2p_z}^{(1)} \pm \chi_{2p_z}^{(2)}\right) \end{split}\]

La representación gráfica de las funciones de onda está en las figuras Fig. 163 y VEE_diat_pi mientras que las energías se pueden ver en el diagrama de niveles, {numref}EE_diat_2p_orb`. De nuevo, como en el caso de la molécula de H\(_2\), podemos comprobar que la probabilidad de encontrar al electrón a un lado u otro del enlace es la misma. Es decir, los electrones en los orbitales 2p son compartidos por igual por los núcleos y el enlace es covalente.

Fig. 165 Diagrama de orbitales moleculares en moléculas diatómicas homonucleares utilizando orbitales 2p. Se puede observar que hay dos orbitales \(\sigma\) uno muy enlazante y otro muy antienlazante y luego pueden observarse 2 pares de orbitales \(\pi\), uno enlazante y otro antienlazante. Dado que los orbitales \(\pi\) aparecen por pares decimos que están doblemente degenerados.

Los autovectores que se han obtenido pueden estudiarse desde el punto de vista de la simetría. Para ello aplicaríamos operaciones de simetría sobre las funciones de onda y veríamos como se transforman para obtener el carácter de la operación y, recompilando todos los caracteres, obtendríamos la irrep del orbital. Se puede comprobar que la solución más baja en energía es un orbital \(\sigma_g\) formado por los dos orbitales \(p_z\) mientras que el más antienlazante es también \(\sigma\) pero impar, \(\sigma_u\) (ver Fig. 163). Por otro lado los orbitales \(p_x\) y \(p_y\) forman las irrep \(\pi_u\), que es enlazante y la \(\pi_g\) que es antienlazante (ver Fig. 163). Observando sus representaciones gráficas podemos ver como en los orbitales enlazantes la interferencia entre los orbitales atómicos es constructiva en la zona central de enlace, mientras que los antienlazantes se caracterizan por tener una interferencia destructiva en la región de enlace. Por último, es importante notar que el hamiltoniano, Ec. (284) es una matriz por cajas donde cada orbital pertenece a una irrep particular, los orbitales \(p_z\) son \(\sigma\) y los orbitales \(p_x\), \(p_y\) son \(\pi\).

Es importante notar que los químicos utilizan el término enlace \(\sigma\) para referirse a un enlace fuerte y \(\pi\) para referirse a uno más débil. Esto está directamente conectado a los resultados anteriores. \(\sigma\) y \(\pi\) son etiquetas que hacen referencia a la simetría y momento angular de las funciones de onda pero, a su vez, tienen que ver con que los orbitales que enlacen estén enfrentados, dando lugar a un fuerte solape (\(\sigma\)) o están más distribuidos en un plano perpendicular al eje de enlace reduciendo el solape (\(\pi\)).

Para estudiar las diferentes características de las moléculas diatómicas el objetivo, ahora, es poblar el diagrama Fig. 165 con electrones y obtener una medida de la fuerza de enlace del mismo.

Orden de enlace

El orden de enlace entre dos átomos es la diferencia entre el número de pares de electrones de esos átomos que ocupan un orbital enlazante y el número de pares de electrones que ocupan un orbital antienlazante.

Por ejemplo, en la molécula de hidrógeno hay un par de electrones que ocupan un orbital enlazante por lo que decimos que su orden de enlace es 1 (hay un par de electrones enlazantes y ninguno antienlazante). En cambio, cuando vemos el diagrama de orbitales de la molécula de He\(_2\) (Fig. 160) hay un orbital enlazante y otro antienlazante ocupados. Por tanto, el orden de enlace es 1-1=0. Esto quiere decir que, bajo la teoría de orbitales moleculares, la molécula de helio no enlaza. Si, en cambio, observamos el ion \(H_2^+\) que tiene un único electrón en un orbital enlazante diremos que su orden de enlace es 0.5, es decir, hay enlace pero es más débil que en H\(_2\).

Evolución de las propiedades

Veamos ahora que ocurre cuando consideramos las moléculas B\(_2\),… Ne\(_2\). El diagrama Fig. 166 muestra la evolución de los orbitales 2s y 2p y como se van llenando según nos movemos de molécula a molécula esencialmente cambiando el número de electrones que contiene el diagrama.

Fig. 166 El diagrama de niveles de la molécula de He\(_2\) neutra.

En la parte inferior del diagrama podemos ver el orden de enlace de la molécula y el símbolo del multiplete fundamental. Empecemos la discusión por la parte derecha del diagrama. Podemos ver que en el \(O_2\) y el \(F_2\) los dos niveles inferiores son \(\sigma_g\) y \(\sigma_u\) que provienen del enlace entre orbitales 2s de forma similar a lo que ocurría en la molécula de hidrógeno. Los orbitales superiores se corresponden con los orbitales 2p discutidos en los apartados superiores. El último orbital que tanto el oxígeno, \(O_2\), como el flúor, \(F_2\) están llenado es el \(\pi_g\) que es antienlazante. Puede observarse que el oxígeno llena 2 orbitales enlazantes más que antienlazantes mientras que el flúor, que tiene 1 par de electrones más que el \(O_2\) que ocupan un orbital antienlazante, tiene un orden de enlace menor, 1. Por tanto, lo que deberíamos esperar es que la distancia internuclear y la fuerza del enlace (energía de disociación) sea más fuerte en el oxígeno que en flúor, como así ocurre.

Podemos ver que para las moléculas a la izquierda en el diagrama hay un cambio en el orden de los niveles que no es el que esperaríamos. Esto es debido a que los orbitales 2s y 2p están muy cerca uno respecto a otro. Esto se debe a que esta separación está relacionada con el número de electrones que contiene un átomo. En el átomo de hidrógeno, donde la energía tan sólo depende del número cuántico principal 2s y 2p están degenerados, en cambio, en el oxígeno o el flúor, que tienen muchos más electrones (8 y 9, respectivamente) esta separación es mucho mayor (varios eV) y lo que separa energéticamente los orbitales 2s y 2p. En el \(N_2\), \(C_2\) y \(B_2\) los orbitales 2s y 2p que generan la misma irrep, \(\sigma_g\), interaccionan fuertemente lo que reduce la energía del orbital inferior (con mayor carácter 2s) y eleva el del superior (con mayor carácter 2p) haciendo que este último se encuentre por encima del orbital \(\pi_u\).

En cualquier caso, podemos observar que la molécula con mayor orden de enlace, 3, es el nitrógeno, \(N_2\) mientras que este valor se reduce según nos vamos alejando del mismo. De este modo podemos predecir que moléculas tienen mayor energía de disociación y menores distancias de enlace. La molécula de Ne\(_2\) tiene orden de enlace 0 y por tanto la teoría predice que no existe.

Algunos ejemplos concretos

Veamos ahora algunos ejemplos concretos y discutamos los diferentes efectos que aparecen en las secciones anteriores.

Molécula de litio

El Li\(_2\) es la molécula más sencilla del segundo periodo. La configuración electrónica de este átomo es \((1s)^2(2s)^1\) por lo que la molécula contiene 6 electrones. Los orbitales 1s y 2s de este átomo están muy separadas energéticamente, además de que el 1s está muy localizado espacialmente, por lo que no participará de forma importante en el enlace ni se mezclará mucho con el 2s del otro átomo. Bajo estas condiciones podemos construir un diagrama de orbitales moleculares donde los orbitales 1s interaccionan entre sí y de forma separada a los 2s.

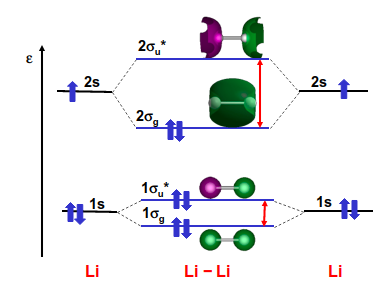
Fig. 167 El diagrama de niveles de la molécula de Li\(_2\) neutra. Los niveles 1s y 2 están muy separados energéticamente.

Podemos ver que cada par de orbitales s forma un orbital enlazante y otro antienlante. Los orbitales moleculares que provienen del 1s son mucho más profundos por lo que serán los primeros que se llenen. Cuando colocamos los 6 electrones de la molécula podemos observar que los orbitales internos se llenan completamente con 4 electrones y, como siempre va a haber el mismo número de orbitales enlazantes que no enlazantes, el resultado es que su aportación al orden de enlace es siempre cero.

Por otro lado, el par de electrones que entran en los orbitales de valencia se colocan en un orbital enlazante que está muy separado del antienlazante. Por tanto, estos electrones estarán apareados en espín y la molécula tendrá \(S=0\), es decir, es no magnética. Como hay un par de electrones en un orbital enlazante su orden de enlace es 1, es decir, se espera que la molécula existe (como realmente hace). Dado que tiene capa cerrada su multiplete fundamental es \(^1\Sigma_g^+\).

Molécula de oxígeno

En el caso del oxígeno (y cualquier otro caso más adelante) vamos a dejar de considerar los orbitales internos ya que estos no participan en el enlace. En esta molécula los orbitales 2s y 2p están muy separados por lo que consideramos que interaccionan por separado. Los orbitales 2s formar un par de orbitales, uno enlazante y otro antienlazante (como en el \(H_2\)) mientras que los 2p forman los niveles descritos en la Fig. 165. Dado que la configuración electrónica del oxígeno es \((1s)^2(2s)^2(2p)^4\) con lo que este diagrama, que no contiene los orbitales internos debe llenarse con 6\(+\)6=12 electrones (ver Fig. 168).

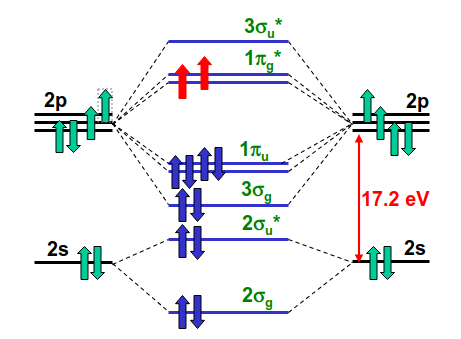
Fig. 168 El diagrama de niveles de la molécula de He\(_2\) neutra.

Haciendo esto podemos ver que llenamos completamente los orbitales \(2\sigma_g\), \(2\sigma_u\), \(3\sigma_g\) y \(1\pi_u\). Los dos últimos electrones van al orbital \(1\pi_g\) donde caben 4. Dado que este orbital está degenerado espacialmente la mejor manera de colocar a los electrones es con los espines paralelos, lo que va a ser más favorable energéticamente. Por tanto, la molécula tendrá \(S=1\) y será (para)magnética. El orden de enlace es 2 debido a que hay 4 orbitales enlazantes ocupados (\(2\sigma_g\), \(3\sigma_g\) y los dos de \(1\pi_u\)) y 2 antienlazantes ocupados (\(2\sigma_u\) y un par de electrones en \(1\pi_g\)).

Para encontrar el multiplete fundamental debemos multiplicar las irreps de los 2 electrones desapareados \(\pi_g\otimes\pi_g\) y el estado resultante es el \(^3\Sigma_g^-\).

Problemas y ejemplos