Estructura en cristales

Ya hemos indicado que los śolidos cristalinos presentan orden a corto alcance, cuando observemos las inmediaciones de dos átomos equivalentes que se encuentren a cierta distancia serán equivalentes, y a largo alcance, lo que significa que no sólo las inmediaciones si no que a grandes distancias la estructura que rodea a un átomo y otro serán iguales.

En lo que sigue introduciremos varios conceptos claves, como son la red, el motivo o las celdas, tanto las primitivas como las convencionales, que son fundamentales para entender las propiedades de los sistemas cristalinos.

Red y Motivo

Para comprender como describir la estructura de un sólido cristalino fijémonos en la Fig. 34 donde se representa un sólido sencillo con periodicidad bidimensional (2D) compuesto de esferas naranjas y verdes que representan átomos. Olvidémonos, por un momento, de la existencia de átomos y pensemos en el sólido como si fuera un dibujo continuo.

Fig. 34 Imagen de un sólido cristalino en 2D sencillo

En la Fig. 34 podemos observar que hay un patrón que se repite de forma regular. En esta frase está la clave para describir la geometría del sólido y nos permite introducir dos conceptos fundamentales:

• Motivo: Es el patrón que se repite. En la Fig. 34 hay varias maneras de escogerlo. En las figuras Fig. 35 y Fig. 36 se muestran dos posibilidades que tienen mucho que ver con lo que luego llamaremos celda.

Fig. 35 Ejemplo de patrón que se repite en el ejemplo del sólido 2D.

Fig. 36 Otra posibilidad para el patrón que se repite en el ejemplo del sólido 2D.

• Red: Son los puntos donde repetimos el patrón para generar todo el sólido. Si tomamos tanto el Fig. 35 como el Fig. 36 y los colocamos en cada uno de los puntos mostrados en la Fig. 37 generaremos una imagen que es la mostrada en la Fig. 34.

Fig. 37 Puntos donde se repiten los patrones para generar el sólido completo.

En la práctica el motivo no será un dibujo si no que será una lista de los átomos, junto con sus coordenadas, que se repite en cada uno de los puntos de la red. Es importante coger habilidad en reconocer los patrones que forman los átomos en los sólidos cristalinos, ya que suele ser el primer paso para poder comprender cualquier propiedad de los mismos.

Veamos ahora la definición más rigurosa, y las propiedades que deben tener, la red y el motivo.

Red de Bravais

Los puntos de la red de un cristal deben estar colocados siguiendo un patrón regular que, para sólidos periódicos en 3 dimensiones (3D), viene dado por,

(39)\[ \vec{R}_{n_1,n_2,n_3}=n_1\vec{a}_1+n_2\vec{a}_2+n_3\vec{a}_3,~\text{donde}~~ n_1, n_2, n_3 \in \mathbb{Z}\]

donde \(\vec{a}_1\), \(\vec{a}_2\) y \(\vec{a}_3\) son vectores no coplanares. Las definiciones para sólidos con periodicidad en el plano (2D) y lineal (1D) son equivalentes simplemente retirando los vectores adecuados.

Las redes que tienen esta forma se denominan redes de Bravais y sus puntos cuentan con las siguientes propiedades:

• Todos ellos son totalmente equivalentes

• Todos ellos tienen la misma orientación

• Los puntos de la red no son átomos ni tienen por qué coincidir con posiciones atómicas Las dos primeras propiedades son claves para identificar si dos puntos pueden pertenecer a la misma red de Bravais (ver cuestión).

Dado un cristal hay muchas maneras de tomar la red de Bravais, tanto cambiando el origen (lo que da lugar, por ejemplo, a los dos patrones Fig. 35, Fig. 36 que discutíamos anteriormente) como la orientación y longitud de los vectores (ver el ejemplo más abajo). En cualquier caso la posición relativa de los puntos de red (como en la Fig. 37 siempre será la misma.

Ejemplo

En el sólido bidimensional que estamos tratando hay varias maneras de tomar la red de Bravais.

Fig. 38 Ilustración de varias maneras que pueden usarse para escoger la red de Bravais para el sólido 2D sencillo del ejemplo inicial.

Usando cualquiera de las parejas de vectores \(\vec{a}_1\), \(\vec{a}_2\) podemos generar el sólido completo si se repiten las áreas marcadas en color rojo (que forman el motivo).

Es fácil de comprobar que los dos motivos más a la derecha tienen el mismo área, que es el doble del motivo más a la izquierda.

Celda primitiva

Se llama celda al volumen contenido en el paralelepípedo que puede formarse con los vectores de red. Las áreas rojas mostradas en la Fig. 38 superior ilustran este concepto. Podemos identificar la celda con el motivo, es la estructura que repetimos para formar el sólido completo.

Llamamos celda primitiva a la celda (o celdas, no hay una única manera de tomarla) más pequeña que podemos usar para reproducir todo el sólido. En el ejemplo, Fig. 38, las dos celdas que se encuentran a la derecha son primitivas mientras que la otra no es primitiva por tener el doble de volumen (área) que las otras.

Convenios en cristalografía

En la discusión anterior hemos podido ver que, aunque ahora podemos describir la geometría de un sólido, hay muchas posibles maneras de tomar los vectores de red y por tanto de definir la celda del sistema. Es, por tanto, importante buscar unos criterios unificados que nos permitan comunicar la estructura de los cristales con eficacia. Este problema es tan importante que hay una Unión Internacional de Cristalografía (ICU) cuya labor es establecer los estándares con los que describimos los cristales y cuyas indicaciones es importante seguir. Todas estas reglas tienen mucho que ver con la simetría del sistema y que, por lo tanto, es clave para entender las propiedades de los materiales.

Sistemas Cristalográficos

La primera de las reglas tiene que ver con la forma en la que debemos escoger la celda de un sólido de una forma estándar y que nos permita interpretarla de forma sencilla. La Unión Internacional de Cristalografía impone restricciones a los tamaños y direcciones relativas de los vectores de red. En general nos indica que debemos escoger los vectores de red con una forma simétrica que viene establecida en las tablas que se dan más abajo.

Ejemplo

En la imagen inferior mostramos otro sólido sencillo en dos dimensiones. ¿Cómo escogeriamos la celda?

Fig. 39 Imagen de otro sólido cristalino en 2D sencillo

En la figura inferior se muestran las dos celdas más importantes para describir el sólido, la inferior tiene el mínimo area y, por tanto, es primitiva. En un principio, para dar las propiedades físicas del sistema, no se necesita ninguna información extra. En cambio la superior capta mejor la simetría rectangular del sólido, aunque tiene el doble de área que la primitiva. Esta es la celda que nos indica la Unión Internacional de Cristalografía que debemos usar, dado que es la celda con la forma adaptada al sistema (rectangular) más pequeña que podemos escoger y es lo que llamamos la celda convencional (su forma ha sido escogida por convenio).

Fig. 40 Ilustración de dos celdas para el sólido sencillo anterior. La inferior es primitiva mientras que la superior es la convencional.

Celda convencional

Todos los cristales van a pertenecer a un sistema cristalográfico. Éste marca, la forma más simétrica que puede tener la celda de un cristal y que va a tener que ver, por ejemplo, con las formas típicas que vamos a poder observar en minerales tallados. La formas de estas celdas, llamadas celdas convencionales, son decididas por consenso en la Unión Internacional de Cristalografía. Las siguientes tablas muestras los diferentes sistemas cristalinos bidimensionales, Fig. 41 y tridimensionales, Fig. 42, junto con la forma de las celdas convencionales.

Como podemos observar en 2 dimensiones hay 4 sistemas cristalográficos, de más alta simetría a menos tenemos el hexagonal, el cuadrado, el rectangular y el oblicuo. Por ejemplo, los vectores de la red convencional del sistema cuadrado siempre tienen el mismo módulo y son ortogonales entre sí. Si podemos escoger entre diferentes tipos de sistema cristalográfico siempre escogeremos el de más alta simetría.

Fig. 41 Tabla de los sistemas cristalográficos con periodicidad en el plano.

En tres dimensiones hay 7 sistemas cristalográficos que son el hexagonal, el cúbico, el tetraédrico, el trigonal, el ortorrómbico, el monoclínico y el triclínico.

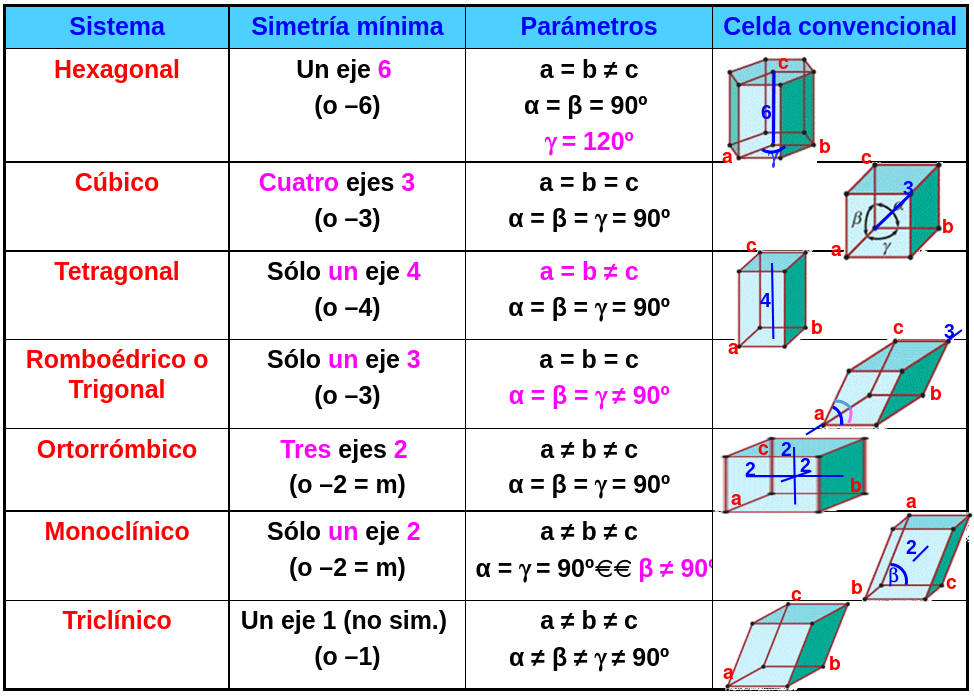
Fig. 42 Tabla de los sistemas cristalográficos con periodicidad en el espacio.

Warning

Aunque en las figuras parezca que la celda convencional de un sistema hexagonal es un hexágono esto no es así. El hexágono que se muestra es una ayuda visual y, realmente, la vista superior de la celda es el paralelepípedo cuyos lados forman 60\(^o\) y 120\(^o\) de forma alternativa (forma roja).

En algunas redes la celda primitiva y la convencional pueden coincidir, en otras la celda convencional repetirá en su interior varios motivos de la red primitiva. Para distinguir entre una y otra utilizaremos los vectores de red \(\vec{a}_1\), \(\vec{a}_2\) y \(\vec{a}_3\) para referirnos a la red primitiva y \(\vec{a}\), \(\vec{b}\) y \(\vec{c}\) para mostrar los vectores de la red convencional.

Cuando tomamos todas las posibles redes de Bravais en tres dimensiones y las clasificamos según los sistemas cristalinos de la tabla tridimensionales, Fig. 42, encontramos la muy importante tabla, Fig. 43, mostrada más abajo. Ahí podemos ver, por ejemplo, que hay 3 tipos de redes cúbicas las primitivas (P), que contienen un sólo punto de red por celda convencional, las centradas en el cuerpo (I, del inglés inside) que tienen un punto de red en los vértices y otro en el centro del cubo formado por los vectores de red y, finalmente, las centradas en las caras (F, del inglés face) que tienen un punto de red en los vértices y otro en el centro de las caras (ver el problema 2 más abajo).

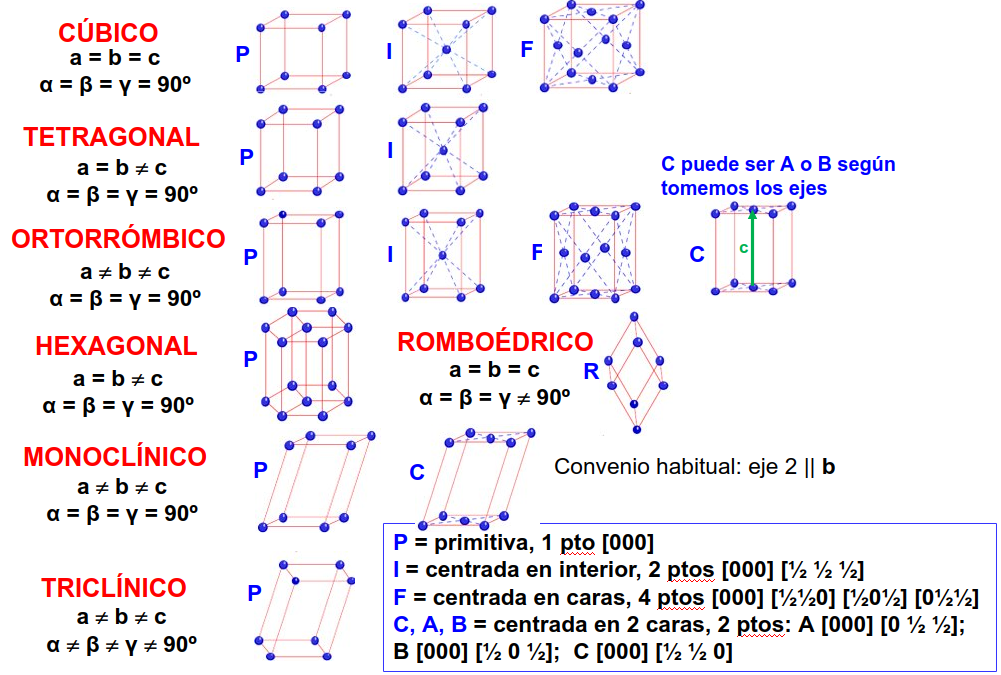
Fig. 43 Tabla de las redes de Bravais en el espacio.

¡Cuidado!

En la figura anterior cada punto representa un punto de red no un átomo. Es decir, donde en el dibujo anterior vemos un punto debemos colocar el motivo completo que, normalmente, contrendrá varios átomos.

Coordenadas fraccionarias

Los datos cristalográficos que pueden encontrarse en bases de datos (ver, por ejemplo, la de la sociedad americana de mineralogía) siempre vienen dados en términos de la celda convencional. Por tanto, los módulos y ángulos entre vectores de red que se encuentran en la misma se refieren a esta celda y nunca a la primitiva.

Del mismo modo el motivo viene dado mediante una lista de coordenadas, \([x,y,z]\), para cada uno de los átomos de la celda, donde la posición del átomo \(\alpha\) (\(\vec{\tau}_\alpha\)) es,

(40)\[ \vec{\tau}_{\alpha}=x_1\vec{a}+x_2\vec{b}+x_3\vec{c} \rightarrow [x_1,x_2,x_3]\]

En la fórmula anterior como los átomos están dentro de la celda \(x_i\in [0,1)\). Es importante darse cuenta que los átomos en posiciones \(x_i+N\), donde N es un entero, son equivalentes a los de la posición \(x_i\). Por ello \(x_i\) siempre será inferior a 1 y nunca inferior a 0.

Ejemplo

Seguidamente presentamos representaciones gráficas de los diferentes tipos de celdas cúbicas, tanto las primitivas (en rojo) como las convencionales (aristas negras y transparentes).

La celda cúbica P (primitiva) tiene la forma de un cubo tanto para la convencional como para la primitiva. Contiene un único punto de red.

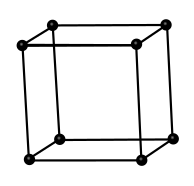
Fig. 44 Ilustración de red cúbica P donde la celda primitiva y la convencional coinciden. Los puntos negros representan puntos de red, no átomos.

(41)\[\begin{split}\begin{matrix} \text{Primitive} &~~~~~~~~~~& \text{Conventional} \\ \vec{a}_1=a \vec{u}_x &~~~~~~~~~~& \vec{a}=a\vec{u}_x \\ \vec{a}_2=a \vec{u}_y &~~~~~~~~~~& \vec{b}=b\vec{u}_y \\ \vec{a}_3=a \vec{u}_z &~~~~~~~~~~& \vec{c}=c\vec{u}_z \end{matrix}\end{split}\]

La celda cúbica I (centrada en el cuerpo) es un cubo en su forma convencional y un paralepipedo más complejo para la primitiva. La celda convencional contiene dos puntos de red de la primitiva, uno en \([0,0,0]\) y otro en \([1/2,1/2,1/2]\).

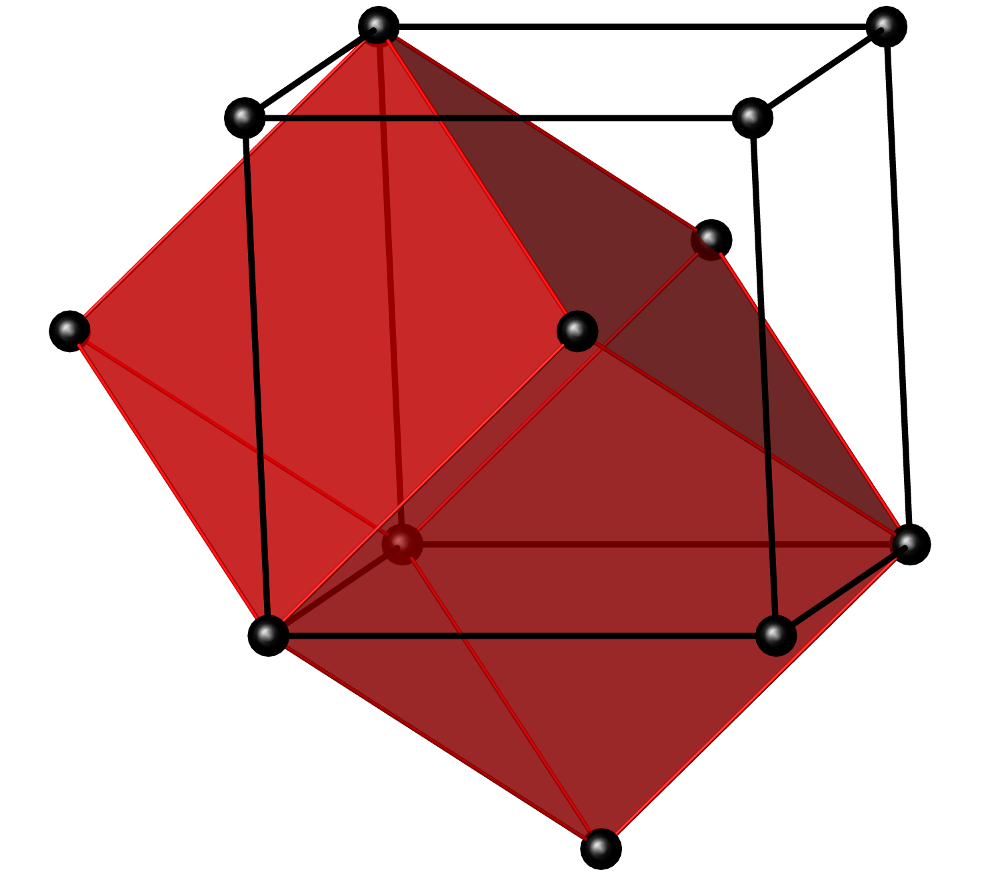
Fig. 45 Ilustración de la red cúbica I. Los puntos de la red primitiva se representan mediante esferas negras, la celda primitiva por un paralelepipedo rojo y la convencional por un cubo de aristas negras.

(42)\[\begin{split}\begin{matrix} \text{Primitive} &~~~~~~~~~~& \text{Conventional} \\ \vec{a}_1=\frac{a}{2} \vec{u}_x + \frac{a}{2} \vec{u}_y + \frac{a}{2} \vec{u}_z &~~~~~~~~~~& \vec{a}=a\vec{u}_x \\ \vec{a}_2=\frac{a}{2} \vec{u}_x - \frac{a}{2} \vec{u}_y + \frac{a}{2} \vec{u}_z &~~~~~~~~~~& \vec{b}=b\vec{u}_y \\ \vec{a}_3=\frac{a}{2} \vec{u}_x + \frac{a}{2} \vec{u}_y - \frac{a}{2} \vec{u}_z &~~~~~~~~~~& \vec{c}=c\vec{u}_z \end{matrix}\end{split}\]

La celda cúbica F (centrada en las caras) es un cubo en su forma convencional y un paralepipedo más complejo para la primitiva. La celda convencional contiene cuatro puntos de red de la primitiva, uno en \([0,0,0]\) y otros en \([1/2,1/2,0]\), \([1/2,0,1/2]\) y \([0,1/2,1/2]\).

Fig. 46 Ilustración de la red cúbica F. Los puntos de la red primitiva se representan mediante esferas negras, la celda primitiva por un paralelepipedo rojo y la convencional por un cubo de aristas negras.

(43)\[\begin{split}\begin{matrix} \text{Primitive} &~~~~~~~~~~& \text{Conventional} \\ \vec{a}_1=\frac{a}{2} \vec{u}_x + \frac{a}{2} \vec{u}_y &~~~~~~~~~~& \vec{a}=a\vec{u}_x \\ \vec{a}_2=\frac{a}{2} \vec{u}_x + \frac{a}{2} \vec{u}_z &~~~~~~~~~~& \vec{b}=b\vec{u}_y \\ \vec{a}_3=\frac{a}{2} \vec{u}_y + \frac{a}{2} \vec{u}_z &~~~~~~~~~~& \vec{c}=c\vec{u}_z \end{matrix}\end{split}\]

Problemas y ejemplos

• Si P es un punto de la red de Bravais en el grafeno, ¿qué otros puntos pertenecen a la misma red?

Fig. 47 Los puntos verdes representan los átomos de carbono en la red de grafeno. Las letras indican posibles posiciones de puntos de la red de Bravais (importante: en general los puntos de la red de Bravais no tienen que coincidir con átomos).

• Cuenta los puntos de red contenidos en una red cúbica P, I y F. Para ello ten en cuenta que un punto de red en el vértice, cara o arista de la celda convencional está compartido entre varias celdas que se tocan por su superficie.