Moléculas diatómicas heteronucleares

En las moléculas que hemos discutido hasta ahora el enlace se producía entre átomos del mismo tipo. Eso quiere decir que los niveles atómicos que participan en el enlace tenían la misma energía, como se ve claramente en el esquema típico para la molécula de hidrógeno (ver Fig. 169).

Fig. 169 El diagrama de niveles de la molécula de H\(_2\) neutra.

En esta sección introduciremos que ocurre cuando los átomos que forman la molécula no son del mismo tipo. Como veremos más abajo la principal diferencia que vamos a tener es que los niveles atómicos de ambos átomos serán, lógicamente, diferentes. Veremos que esto afecta a la altura de los niveles pero también, y de forma muy importante, a la distribución de carga de la molécula ya que habrá átomos que tomarán carga de otros que la cedan. Por tanto, introduciremos el concepto de enlace iónico que contrastará con el que hemos discutido hasta ahora, el enlace covalente, donde los electrones se tendían a colocar en la zona central del enlace siendo compartidos por ambos átomos. Es importante indicar aquí que ningún enlace será totalmente iónico dado que siempre existirá una cierta compartición de carga. La magnitud que será determinante para encontrar como de iónico será un cierto enlace será la electronegatividad.

Electronegatividad

Hay un buen número de magnitudes que podemos utilizar para medir como de afín es un cierto átomo (o ion) a ceder o recibir electrones. Desde el punto de vista energético las más importantes son la energía de ionización y la afinidad electrónica.

Definición: La energía de ionización (EI) es la energía que hay que darle a un átomo o ion para arrancarle un electrón.

(287)\[X^{n}+EI\rightarrow X^{n+1} + e^{-}\]

Definición: La afinidad electrónica (AE) es la energía que libera un átomo al capturar un electrón.

(288)\[X^{n}+e^{-}\rightarrow X^{n-1} + AE\]

Tanto la energía de ionización como la afinidad electrónica están ligadas a la energía con la que los electrones de la última capa están ligados en el átomos. Por tanto, ambas crecen con la carga efectiva nuclear \(Z^*\) y el número cuántico principal, es decir que cuanto más arriba y a la derecha de la tabla periódica se encuentre el átomo más grande serán (salvo la AE para los gases nobles).

Los químicos tratan de condensar parte de la información contenida en estos valores en una magnitud llamada electronegatividad, \(\chi\), que indica la capacidad de un átomo para atraer los electrones hacia ellos. Existen varias escalas diferentes, aunque la más usada es la de Pauling que define la diferencia de electronegatividades entre dos átomos del siguiente modo,

(289)\[\vert \chi_A -\chi_B\vert = \frac{1}{ \sqrt{1eV}} \sqrt{E_d(AB)-\frac{E_d(AA)+E_d(BB)}{2}}\]

donde la electronegatividad es una magnitud adimensional y \(E_d\) son las energías de disociación (en eV) de las moléculas formadas por los átomos A y B por separado o juntas (AA, BB). Dado que la escala trabaja en diferencias se utilizó una referencia arbitraria eligiendo el valor para el hidrógeno como 2.2 y siendo el flúor el elemento con mayor electronegatividad (4.0), ver Fig. 170.

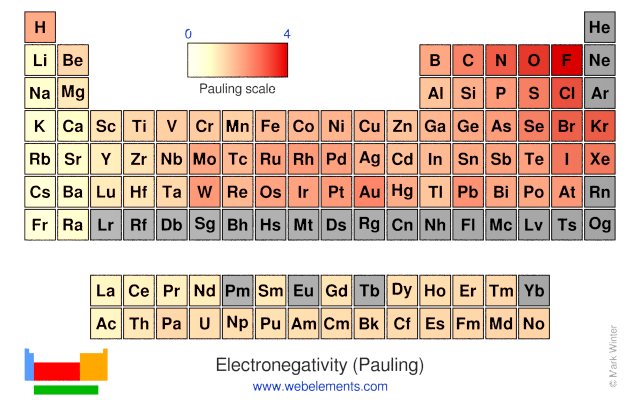
Fig. 170 Tabla periódica donde el color de fondo en cada elemento sigue la escala de electronegatividad. Es importante observar como los elementos más arriba a la derecha tienen los mayores valores en la escala. Figura obtenida de webelements.

De forma práctica, tomaremos la electronegatividad de los átomos como un indicador de que niveles atómicos deberemos colocar más abajo en nuestros diagramas ya que serán los niveles que se tenderán a poblar con electrones.

Moléculas heteronucleares

Imaginemos ahora que ocurriría si en vez de tener una molécula de H\(_2\) o de Li\(_2\) tuviéramos una molécula de LiH. Ambos átomos participan en el enlace con su orbital de valencia, 1s en el caso del hidrógeno y 2s en el caso del litio. El hidrógeno con una electronegatividad \(\chi_H=2.2\) es más electronegativo que el litio con \(\chi_{Li}=0.98\). Eso quiere decir que el hidrógeno atraerá más a los electrones en la molécula y tenderá a estar cargado negativamente, mientras que el litio tendrá una carga parcial positiva.

De forma cuantitativa esto quiere decir que el elemento diagonal del orbital 1s del hidrógeno, \(\varepsilon_H=\left\langle \chi_H \right\vert \hat{h} \left\vert \chi_H \right\rangle\) tiene una energía menor que la del correspondiente elemento diagonal, \(\varepsilon_{Li}=\left\langle \chi_{Li} \right\vert \hat{h} \left\vert \chi_{Li} \right\rangle\), para el orbital del litio,

(290)\[\varepsilon_H = \left\langle \chi_H \right\vert \hat{h} \left\vert \chi_H \right\rangle < \left\langle \chi_{Li} \right\vert \hat{h} \left\vert \chi_{Li} \right\rangle = \varepsilon_{Li}\]

Por otro lado, dado que los orbitales 1s del H y 2s del Li tienen un solape no nulo el elemento no diagonal de interacción (hopping) es,

(291)\[\gamma = \left\langle \chi_H \right\vert \hat{h} \left\vert \chi_{Li} \right\rangle = \left\langle \chi_{Li} \right\vert \hat{h} \left\vert \chi_{H} \right\rangle. \]

Por tanto, la matriz hamiltoniana es,

(292)\[\begin{split}h= \begin{pmatrix} \varepsilon_H & \gamma\\ \gamma & \varepsilon_{Li} \end{pmatrix}\end{split}\]

y sus autovalores y autovectores son,

(293)\[\varepsilon_0=\frac{(\varepsilon_H+\varepsilon_{Li})-\sqrt{(\varepsilon_H+\varepsilon_{Li})^2-4(\varepsilon_H\varepsilon_{Li}-\gamma^2)}}{2}\]

y

(294)\[\vert\psi_0\rangle=c_{0H}\chi_a\rangle + c_{0Li}\vert \chi_b \rangle,~\vert c_{0H}\vert > \vert c_{0Li}\vert\]

mientras que el orbital más alto es,

(295)\[\varepsilon_0=\frac{(\varepsilon_H+\varepsilon_{Li})+\sqrt{(\varepsilon_H+`\varepsilon_{Li})^2-4(\varepsilon_H\varepsilon_{Li}-\gamma^2)}}{2}\]

y

(296)\[\vert\psi_0\rangle=c_{1H}\chi_a\rangle - c_{1Li}\vert \chi_b \rangle,~\vert c_{0H}\vert < \vert c_{0Li}\vert\]

Es sencillo ver que estas energías orbitales cumplen dos propiedades,

• La energía de \(\varepsilon_0\) es inferior al valor del elemento diagonal más bajo de la matriz (\(\varepsilon_H\)) y, a la vez, \(\varepsilon_1\) es superior al valor del elemento diagonal más alto de la matriz (\(\varepsilon_{Li}\))

• El cambio en energía orbital debido a la parte no diagonal de la energía hamiltoniana es menor que el cambio que había en la molécula homonuclear (que era \(\gamma\)). Es decir, la parte de enlace covalente en una molécula heteronuclear no es tan efectiva como en una homonuclear. Mientras tanto los autovalores cumplen lo siguiente:

• En la solución más baja el coeficiente del elemento más electronegativo (\(c_{0H}\)) es mayor en valor absoluto que el del menos electronegativo (\(c_{0Li}\). Esto hace que la probabilidad de encontrar a la pareja de electrones que ocupa el nivel inferior sobre el hidrógeno sea mayor que la de encontrarla sobre el litio indicando que el enlace es polar y que hay un grado de ionicidad en el mismo.

• En cambio, en la solución más alta el coeficiente del elemento más electronegativo (\(c_{0H}\)) es menor en valor absoluto que el del menos electronegativo (\(c_{0Li}\). Esto hace que la probabilidad de encontrar a la pareja de electrones que ocupa este nivel sobre el hidrógeno sea menor que sobre el litio. Evidentemente, como la energía del nivel del litio es superior esto es una situación desfavorable desde el punto de vista energético.

En la Fig. 171 se muestra un esquema de niveles moleculares que proviene de esta resolución y donde se ilustran estas propiedades.

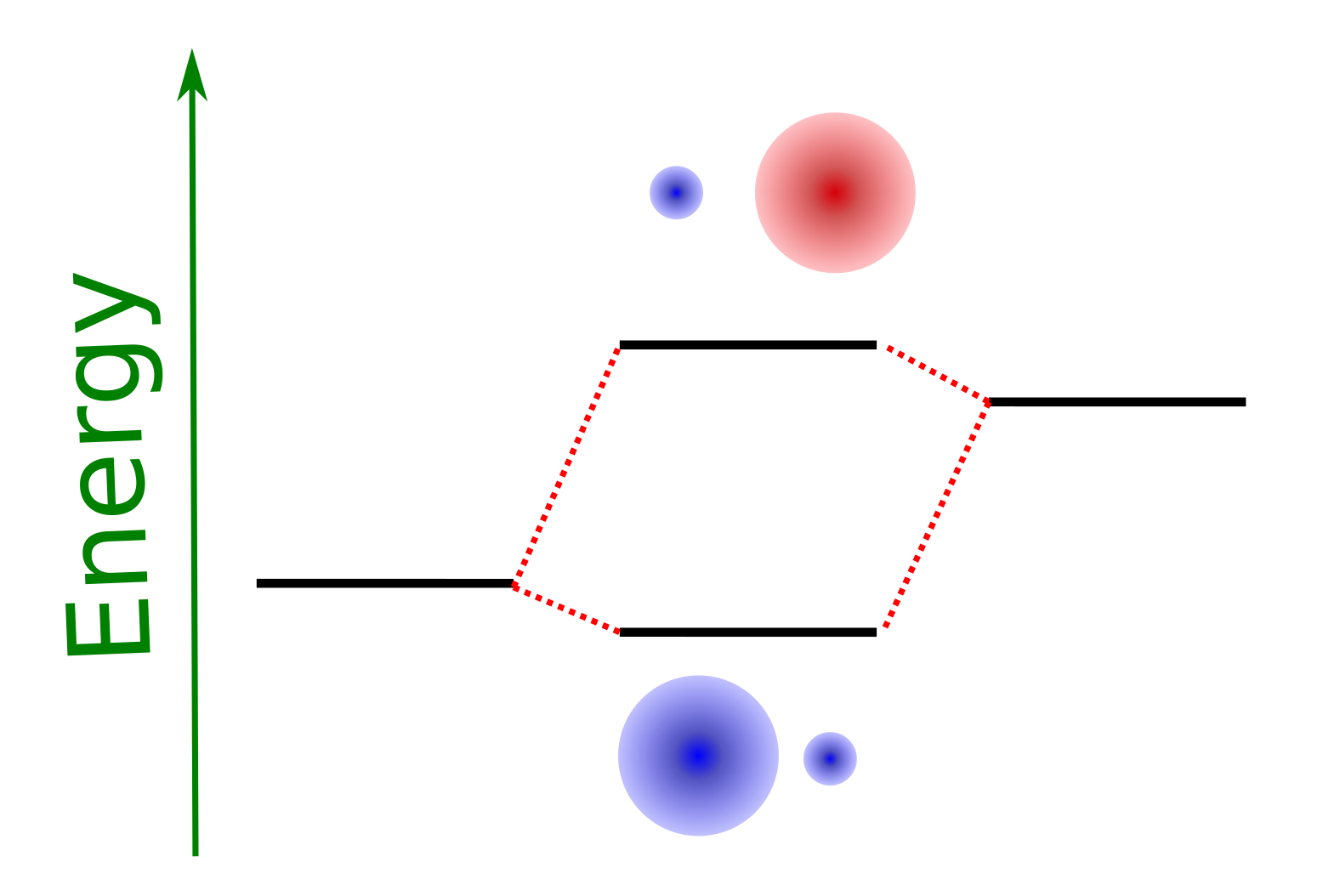
Fig. 171 Esquema de niveles para la molécula de LiH. El nivel atómico del hidrógeno estaría a la izquierda y es más profundo que el del litio (a la derecha) debido a su mayor electronegatividad. Debido a que los orbitales solapan hay un corrimiento de energía que depende, esencialmente de \(\gamma\) y lo separados que están los niveles (\(\varepsilon_H-\varepsilon_{Li}\)).

Electrostática

Dada la transferencia de carga habrá un átomo que tendrá una carga neta positiva (el menos electronegativo) y otro con una carga neta negativa (el más electronegativo). Esto hace que ambos átomos se vuelvan iones. Los iones producen un potencial electrostático que tiene largo alcance. Un ion positivo produce un potencial positivo a su alrededor que hace que la energía de un electrón decrezca,

(297)\[\Delta\varepsilon=-eV\]

En cambio un ion negativo hace que el potencial alrededor suyo sea negativo y la energía de los electrones, por la fórmula anterior crezca. Por tanto, los niveles del ion negativo (anión) se estabilizarán debido a la presencia del ion positivo cercano mientras que los del ion positivo (catión) se desestabilizarán debido a la cercanía del anión. Dado que los niveles del anión están ocupados por más electrones que los del catión y que las interacciones electrostáticas descritas aquí hacen que los niveles atómicos bajen aún más el efecto conjunto es que el enlace entre el anión y el catión se refuerza (los iones de distinto signo sufren una fuerza atractiva entre sí de naturaleza electrostática). Cuanto mayor sea la diferencia de electronegatividad y cuanto mayor sea la carga formal de los iones más fuerte será el enlace.

Molécula de fluoruro de litio

Podemos considerar ahora la molécula de fluoruro de litio. Como en los anteriores casos esperamos que las capas internas del flúor (el orbital 1s) y del litio (otro orbital 1s) no interaccionen entre sí y se mantengan, aproximadamente, en la misma energía electrónica como su elemento atómico (ver Fig. 172).

Respecto a la capa de valencia tenemos la configuración del flúor \((2s)^2 (2p)^7\) y la del Li \((2s)^1\). Es decir, debemos considerar 1 orbital 2s y 3 2p del flúor y 1 orbital 2s del litio. El elemento diagonal del orbital 2s del flúor será \(\varepsilon_{F,s}\) y los 2p, \(\varepsilon_{F,p}\), mientras que el 2s del litio será \(\varepsilon_{Li,s}\). Desde el punto de vista energético tenemos que el flúor es mucho más electronegativo (\(\chi_F=4.0\)) que el litio (\(\chi_{Li}=0.98\)), es decir, tendremos las siguientes relaciones,

(298)\[\varepsilon_{Li,s}> \varepsilon_{F,p}> \varepsilon_{F,s}\]

Dado que el flúor contiene muchos electrones la separación entre el 2p y el 2s es muy considerable (15-20eV) por lo que estos dos orbitales no se mezclaran mucho. Dado que el orbital del litio está por encima del 2p la interacción 2s-2s entre el flúor y el litio podemos predecir que va a ser muy débil.

Si consideramos ahora la parte no diagonal del Hamiltoniano tenemos que observar que orbitales del flúor pueden solapar con los del litio. En principio los orbitales 2s pueden solapar entre sí, dando lugar al elemento \(\gamma_{ss}\), aunque la mezcla será muy débil debido a la gran diferencia de energía. Después podemos observar que el orbital 2s del litio solapa muy direccionalmente con el orbital \(2p_z\) del litio con lo que esperamos una integral \(\gamma_{sp_z}\) no nula y relativamente grande. Finalmente el solape del orbital 2s del litio con el \(2p_x\) y \(2p_y\) es nula (el primero es un orbital que pertenece a la irrep \(\sigma\) mientras que los segundos perteneces a \(\pi\)). Por tanto, la matriz hamiltoniana sería,

(299)\[\begin{split}h= \begin{pmatrix} \varepsilon_{F,s} & 0 & 0 & 0 & \gamma_{ss}\\ 0 & \varepsilon_{F,p} & 0 & 0 & 0\\ 0 & 0 & \varepsilon_{F,p} & 0 & 0\\ 0 & 0 & 0 & \varepsilon_{F,p} & \gamma_{sp_z}\\ \gamma_{ss} & 0 & 0 & \gamma_{sp_z} & \varepsilon_{Li,s} \end{pmatrix}\end{split}\]

Viendo la matriz superior podemos concluir (ver Fig. 172) que habrá orbitales moleculares con un carácter casi puro de orbital 2s del litio y del flúor (ambos de tipo \(\sigma\)) y otros con carácter 2\(p_x\) y \(2p_y\) (de tipo \(\pi\)). Finalmente, la interacción entre el orbital \(2p_z\) del flúor y 2s del litio dará lugar a un orbital enlazante cercano al flúor (\(\sigma\)) y otro antienlazante (\(\sigma^*\)) cercano al hidrógeno.

Fig. 172 Diagrama de niveles de la molécula de fluoruro de litio obtenida mediante cálculos de primeros principios. Puede observarse que los niveles atómicos \(2p_z\) del fluor y \(2s\) del litio interaccionan fuertemente para formar un enlace polar. El \(2s\) del litio y el \(2s\) del fluor también interaccionan, aunque muy debilmente debido a su gran diferencia energética. El resto de los niveles son cuasiatómicos.

Problemas y ejemplos