Producto de irreps

En esta última sección se va a discutir cuál es la irrep de un producto de funciones. Esto tiene dos aplicaciones directas muy importantes. La primera es que, hasta ahora, tan sólo hemos discutido las irreps de los orbitales a 1 electrón pero no de las funciones que contienen muchos electrones como, por ejemplo, los determinantes de Slater. Por otro lado, la simetría del producto de irreps nos va a permitir determinar que integrales son nulas (o no) por simetría, algo que tiene mucha importancia para determinar, por ejemplo, que líneas de un espectro de absorción pueden observarse experimentalmente.

Simetría de las funciones producto

Empecemos suponiendo, que las funciones que tenemos son los autovectores de las operaciones de simetría. En ese caso, si aplicamos una operación de simetría sobre un producto de funciones tenemos que aplicar la operación, simultáneamente sobre cada uno de los elementos del producto,

(238)\[\hat{O} \phi_1 (\vec{r})\phi_2\phi_3 (\vec{r})\cdots\phi_N (\vec{r}) = o_1 o_2 \cdots o_N \phi_1 (\vec{r})\phi_2\phi_3 (\vec{r})\cdots\phi_N (\vec{r})\]

Por tanto, podemos ver que el carácter del producto de las funciones es el producto de los caracteres de las funciones que lo forman.

Veamos ahora como se puede encontrar las irreps generadas en un producto de forma más general. Si tenemos el producto de las funciones \(\psi_i^\ell\) y \(\psi_{i^\prime}^{\ell^\prime}\) decimos que su producto genera la representación \(\Gamma\) que es producto directo de la de \(\Gamma^\ell\) y \(\Gamma^{\ell^\prime}\),

(239)\[\Gamma=\Gamma^\ell \otimes \Gamma^{\ell^\prime}\]

Si al aplicar una operación de simetría sobre los orbitales \(\psi_i^\ell\) y \(\psi_{i^\prime}^{\ell^\prime}\) tenemos, en forma matricial,

(240)\[\begin{split}\begin{matrix} R\psi_i^\ell=\sum_j \psi_j^\ell D_{ji}^\ell(R) \\ R^\prime \psi_{i^\prime}^{\ell^\prime}=\sum_{j^\prime} \psi_{j^\prime}^{\ell^\prime} D_{j^\prime i^\prime}^{\ell^\prime}(R^\prime) \end{matrix}\end{split}\]

donde \(D_{ji}^\ell(R)\) y \(D_{j^\prime i^\prime}^{\ell^\prime}(R^\prime)\) son las matrices asociadas a la operación R en la representación D. Cuando hagamos el producto de las funciones tendremos que la matriz que caracteriza la transformación es,

(241)\[\psi_i^\ell \psi_{i^\prime}^{\ell^\prime} \rightarrow D_{ij}^\ell(R) D_{i^\prime j^\prime}^{\ell^\prime}(R^\prime).\]

Podemos calcular ahora el carácter de la operación de simetría R en la representación del producto directo tomando la traza de la matriz producto,

(242)\[\chi(R)= \sum_{i}\sum_{i^\prime} D_{ii}^\ell(R) D_{i^\prime i^\prime}^{\ell^\prime} (R^\prime) = \chi^\ell(R) \chi^{\ell^\prime}(R^\prime)\]

Es decir, que el carácter de la operación es el producto de los caracteres de las funciones que lo forman, tal y como adelantábamos en la Ec. (238). A partir de esto, y aplicándolo sobre todas las operaciones podríamos encontrar las irreps generadas por un producto de irreps.

Tablas de productos de irreps

De forma práctica realizar en cada caso los productos de los caracteres de las irreps es muy largo y estos resultados se pueden encontrar en tablas de caracteres como las de Atkins. En la Fig. 146 mostramos la tabla de caracteres junto a una tabla de productos directos para cada una de las irreps del grupo \(C_{3v}\).

Fig. 146 Tabla de caracteres para el grupo \(C_{3v}\) (izquierda) y su tabla de productos directos asociada (derecha).

En esta tabla podemos ver algunas propiedades importantes de los productos de irreps:

• El producto de cualquier irrep por la totalmente simétrica da, como resultado, la irrep inicial.

• El producto de cualquier irrep por si misma dará siempre, al menos, la irrep totalmente simétrica.

• La dimensión del producto es el producto de las dimensiones de las irreps. Si multiplicamos irreps unidimensionales como \(A_1\) o \(A_2\) entre sí dará una única irrep. En el caso de multiplicar una irrep de dimensión 2 por ella misma,

(243)\[E\otimes E = A_1 + [A_2] + E\]

el resultado tiene dimensión 4 (\(A_1\) tiene dimensión 1, \(A_2\) dimensión 1 y \(E\) tiene dimensión 2).

Símbolo del multiplete

Podemos encontrar ahora la irrep a la que pertenece un estado multielectrónico que viene descrito por una configuración electrónica, es decir, una lista de orbitales ocupados.

Es sencillo probar que, si todas las capas de la molécula están completas la irrep del multiplete es \(A_1\). La idea es que en una capa cerrada todos los orbitales espaciales contienen dos electrones con espines opuestos. Cuando multiplicamos una irrep por si misma siempre obtenemos \(A_1\) y este es el único resultado posible en una capa cerrada.

Una vez que sabemos esto, podemos imaginarnos muchas configuraciones de moléculas como una capa cerrada a la que hemos añadido o sustraído uno o más electrones. Estos electrones van a ser los que determinen la simetría del estado multielectrónico. La clave está en que la irrep de la capa cerrada es \(A_1\) por lo que, cuando añadamos (o quitemos) un electrón que ocupa un orbital con irrep \(\gamma\), la irrep del conjunto será:

(244)\[\Gamma(\Psi)=A_1 \otimes \gamma = \gamma\]

Es decir que los estados con un electrón desapareado tienen la simetría de este electrón (ver ejemplo más abajo).

Si tuviéramos dos electrones desapareados la irrep del estado multielectrónico sería la de todos los electrones apareados (\(A_1\)) multiplicada por la del primer electrón desapareado, \(\gamma_1\), por la del segundo electrón desapareado, \(\gamma_2\),

(245)\[\Gamma(\Psi)=A_2 \otimes \gamma_1 \otimes \gamma_2 = \gamma_1 \otimes \gamma_2\]

De esta manera podríamos determinar la irrep de los estados multielectrónicos.

Notación: estados a un electrón frente a estados multielectrónicos

Los estados a un electrón vienen descritos por un símbolo \(nx^s\) donde:

• x es una etiqueta, la de su irrep, en minúscula

• n indica lo profundo que es el nivel. En el nivel con menor energía perteneciente a una irrep n=1, en el segundo n=2, etc.

• si los estados son antienlazantes (ver el tema sobre enlace químico en moléculas diatómicas) se pueden marcar con un asterisco como superíndice, \(s=\star\), o ninguno si son enlazantes.

Por ejemplo, el 5 orbital perteneciente a la irrep \(A_2\) se denotaría \(5a_2\) si es enlazante y \(5a_2^\star\) si es antienlazante.

Los estados multielectrónicos vienen descritos según un símbolo \(^{2S+1}X\) donde,

• X es la etiqueta de la irrep del estado multielectrónico

• S es el espín total de la molécula

En una molécula usual con todas sus capas cerradas el estado fundamental es \(^1A_1\) dado que el espín total es 0. Un complejo de metal de transición octaédrico con 8 electrones en la capa d tiene como estado fundamental un estado \(^3A_2\), es decir, un triplete de espín.

Ejemplo: Multipletes en el \(F_2\) y sus iones

Fig. 147 Diagramas de orbitales moleculares de la molécula de fluor neutra (\(F_2\)), su anión, \(F_2^-\), y su catión, \(F_2^+\).

Discutamos ahora cuales son los estados fundamentales de la molécula de \(F_2\) y sus multipletes. Estos estados se muestran en la figura superior.

Podemos ver que la molécula neutra (figura central) tiene su capa cerrada y su espín es cero, por lo que su símbolo del multiplete es totalmente simétrico, que en el grupo \(D_{\infty h}\), se corresponde con \(^1\Sigma_+\) (en vez de \(^1A_1\), ver tabla de caracteres).

En cambio, el ión positivo tiene un hueco (la falta de un electrón) en la capa \(1\pi_g^\star\) por lo que el estado multielectrónico pertenece a la irrep \(\Pi_g\). Además el estado tiene un electrón desapareado por lo que su espín es \(S=1/2\rightarrow 2S+1=2\). El símbolo de multiplete es \(^2\Pi_g\).

Finalmente, el anión tiene un electrón desapareado en la capa \(3\sigma_u^\star\) por lo que el símbolo de multiplete será \(^2\Sigma_u\), un doblete de espín dado que el electrón puede tener el espín hacia arriba o hacia abajo y ambas posibilidades están degeneradas.

Multiplicidad de espín

La multiplicidad de espín, \(2S+1\), indica cuantas proyecciones posibles (valores de \(S_z\)) puede tener un estado con espín \(\vert \vec{S} \vert = S\) (\(S_z=-S,-S+1\cdots S+1,S\)). Esto es fácil de visualizar con S=0, la capa está cerrada y no hay espín, con lo que hay una sóla posibilidad. Con \(S=1/2\) tenemos un electrón desapareado que puede estar hacia arriba o hacia abajo, \(S=1/2\rightarrow S_z=-1/2~ o S_z=1/2\). Valores más altos de espín implican tener que proyectarlo según precesa y son algo más difíciles de visualizar.

Integrales que se anulan por simetría

Otra importante pregunta es si la integral,

(246)\[p_{ab}=\left\langle \phi_a \right\vert \hat{P} \left\vert \phi_b \right\rangle\]

será nula o no nula. La simetría puede ayudar a dar una respuesta a esta pregunta. Para ello vamos a aplicar una operación de simetría a la integral,

(247)\[\hat{R}p_{ab}=\left\langle \hat{R}\phi_a \right\vert \hat{R}\hat{P} \left\vert \hat{R}\phi_b \right\rangle\]

dado que la integral es un escalar una operación de simetría no puede cambiarla, por lo que,

(248)\[\hat{R}p_{ab}=p_{ab}\]

La integral se transformara como el producto de las irreps de \(\phi_a\), \(\hat{P}\) y \(\vec{\phi_b}\), es decir,

(249)\[\hat{R}p_{ab}=p_{ab}=\left\langle \hat{R}\phi_a \right\vert \hat{R}\hat{P} \left\vert \hat{R}\phi_b \right\rangle= \chi_{a} \chi_{p} \chi_p \left\langle \phi_a \right\vert \hat{P} \left\vert \phi_b \right\rangle= \chi_{a} \chi_{p} \chi_p p_{ab}\]

La única posibilidad de que \(p_{ab}\) no sea cero es que el producto \(\chi_a \chi_p \chi_b\) sea 1 para todas las operaciones de simetría y eso implica que el producto debe expandir la irrep totalmente simétrica. Es decir, que para que la integral \(p_{ab}\) sea no nula debe cumplirse,

(250)\[\Gamma_a \otimes \Gamma_p \otimes \Gamma_b \subset A_1\]

Paridad

Aunque entender por qué una integral sea cero o no por simetría puede parecer complejo, realmente es muy similar a una conocida regla que indica que las integrales (a todo el espacio) de funciones impares son nulas y las pares son no nulas (ver figura inferior).

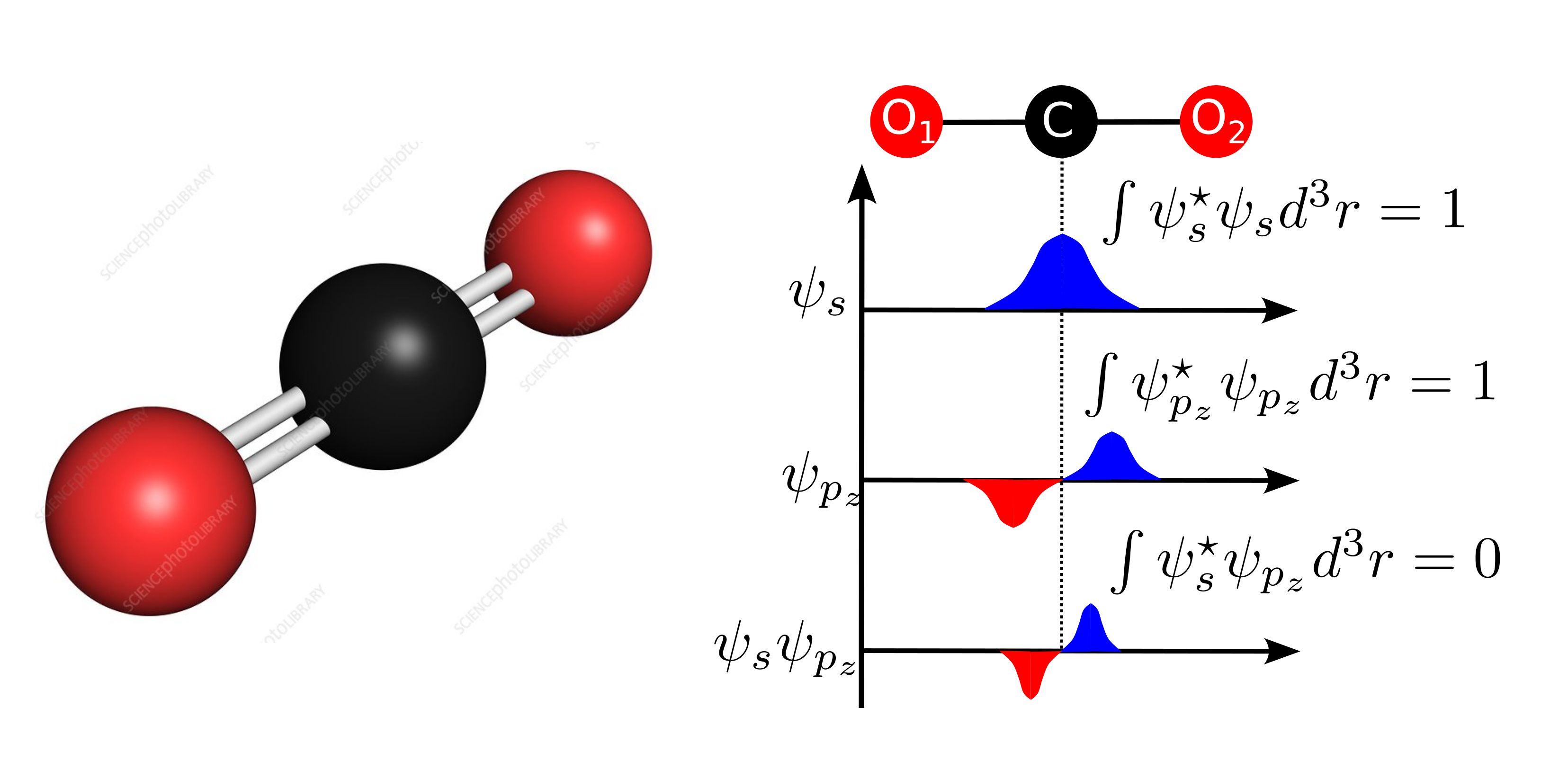
Fig. 148 Representación gráfica de algunas funciones en la molécula de CO\(_2\) y el efecto de la simetría de estas en algunas integrales ue pueden anularse o no dependiendo de si el integrando es par o impar.

Supongamos la integral de solape entre funciones \(2s\) y \(2p_z\) del carbono en el CO\(_2\). La función 2s es par (su etiqueta es \(\Sigma^+_g\), donde la g viene de gerade, que es par en alemán)) mientras que \(2p_z\) es impar (su etiqueta es \(\Sigma_u^+\), la u viene de ungerade, impar en alemán).

El producto de dos funciones pares es par (en las tablas de caracteres \(g\otimes g =g\)) pero también lo es de dos funciones impares (\(u\otimes u =g\)). En cambio, el producto de una función par por una impar, como se muestra en la figura, es impar \(g \otimes u = u\). Esto quiere decir que el solape de 2s con 2s o de \(2p_z\) con \(2p_z\) será no nulo pero el de \(2s\) con \(2p_z\) sí es cero dado que el resultado es una función impar y al integrar a los dos lados del origen obtendremos el mismo resultado pero con signos diferentes (ver figura).

Problemas y ejemplos