Ion hidrógeno molecular

Como ya se indico anteriormente la molécula más sencilla es el ion \(H_2^+\). Esta molécula tan sólo cuenta con dos núcleos (de hidrógeno) y un electrón, tal y como está representado en la Fig. 149.

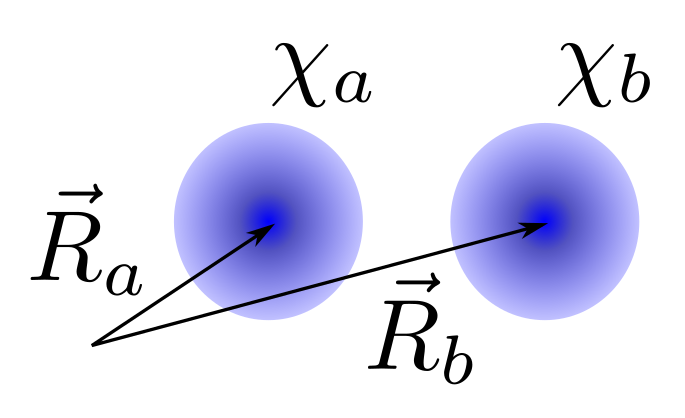
Fig. 149 Posiciones de los orbitales 1s en la molécula de H\(_2\) centrado, cada uno, alrededor de un núcleo (a y b) de la molécula.

Aunque el problema conjunto (2 núcleos+1 electrón) no es resoluble exactamente, con la aplicación de la aproximación adiabática el problema electrónico sí que es resoluble, tal y como lo podemos encontrar en los libros de Slater[7]. Aquí seguiremos otra estrategia, ya que queremos usar la teoría LCAO, que será válida para todo tipo de moléculas.

Base atómica para teoría LCAO

El primer paso para usar la teoría LCAO es determinar que base utilizaremos para representar los orbitales moleculares, solución de la ecuación de Hartree-Fock. En el caso del hidrógeno el orbital de valencia es el 1s, por lo que tomaremos uno de estos orbitales por cada átomo de hidrógeno en la molécula (es decir, dos orbitales 1s en total, representados por esferas azules en la Fig. 149). Denominaremos a estos orbitales \(\chi_a\) y \(\chi_b\).

Dado que los orbitales atómicos son soluciones de la ecuación de Schrödinger para el átomo de hidrógeno estas funciones de onda están normalizadas, de modo que,

(252)\[S_{aa}=S_{bb}=1\]

Recordando la expresión de los orbitales atómicos 1s del hidrógeno,

(253)\[\chi(\vec{r})=\frac{1}{\sqrt{\pi}}\frac{1}{a_0^{3/2}}e^{-r/a_0}\]

podemos encontrar la integral de solape,

(254)\[S_{ab}=\left\langle \chi_a \right\vert \left. \chi_b \right\rangle = \int \chi_a^*(\vec{r})\chi_b(\vec{r}) d^3r\]

que adquiere el valor (en unidades atómicas),

(255)\[S=S_{ab}=S_{ba}=e^{-R}\left(1+R+\frac{R^2}{3}\right)\]

Como podemos comprobar, el solape es fuertemente dependiente de la separación espacial de los dos átomos dada por R.

Matriz Hamiltoniana

El segundo paso para resolver la ecuación de Hartree-Fock es encontrar la matriz hamiltoniana,

(256)\[h_{ab}=\left\langle \chi_a \right\vert \hat{h} \left\vert \chi_b \right\rangle \]

Para resolver las integrales usando el orbital Ec. (253) es importante recordar que la energía del orbital 1s del hidrógeno es \(E_H=-13.6\) eV. Por otro lado tenemos que,

(257)\[J=\left\langle \chi_a \right\vert \frac{1}{\vert \vec{r}-\vec{R}_b\vert}\left\vert\chi_a\right\rangle = -E_H\frac{2}{R}\left[1-e^{-2R}(1+R)\right]>0\]

es la interacción electrón-núcleo sobre el mismo átomo y,

(258)\[K=\left\langle \chi_a \right\vert \frac{1}{\vert \vec{r}-\vec{R}_a\vert}\left\vert\chi_b\right\rangle = -E_H\frac{2}{R}\left[1-e^{-2R}(1+R)\right]>0.\]

es la interacción electrón núcleo que afecta al salto entre orbitales de diferentes átomos, el hopping.

Usando estas integrales y observando que, dado que los dos átomos de hidrógeno son equivalentes, los elementos hamiltonianos diagonales son iguales entre sí. Usando las integrales anteriores,

(259)\[\varepsilon_H=h_{aa}=h_{bb}=E_H+\frac{1}{R}-J.\]

Podemos ver que la contribución principal al elemento diagonal de matriz es la energía del átomo de hidrógeno, lo cual es consistente con ser el valor esperado de cierto orbital atómico \(\chi_a\). Este valor no es exclusivamente el atómico si no que viene corregido por el hecho de que el orbital ahora se encuentra dentro de una molécula por lo que la posición del resto de los núcleos afecta a la energía de este orbital atómico debido a los potenciales electrostáticos incluidos en \(1/R\) y J.

Para los elementos no diagonales del Hamiltoniano se obtiene,

(260)\[\gamma=h_{ab}=h_{ba}=\left(E_H+\frac{1}{R}\right)S-K\]

donde observamos que los elementos no diagonales son también iguales, dado que el operador Hamiltoniano es hermítico (es decir, si es real también es simétrico). Además el valor del elemento no diagonal es fuertemente dependiente del solape, un hecho que utilizaremos de forma repetida en las próximas secciones.

Solución de la ecuación de Hartree-Fock

Podemos ahora tomar la ecuación de Roothan-Hartree-Fock (Ec. (158)) y escribirla del siguiente modo,

(261)\[\hat{h}\vec{c}_i = \varepsilon_i \vec{S}\vec{c}_i \rightarrow \left(\hat{h}-\varepsilon_i \hat{S}\right)\vec{c}_i=0\]

Usando explícitamente notación matricial y sustituyendo los elementos diagonales por la energía modificada del orbital 1s del hidrógeno, \(\varepsilon_H\), y el hopping por \(\gamma\), se obtiene,

(262)\[\begin{split}\begin{pmatrix} h_{aa}-\varepsilon_i S_{aa} & h_{ab}-\varepsilon_i S_{ab}\\ h_{ba}-\varepsilon_i S_{ba} & h_{bb}-\varepsilon_i S_{bb} \end{pmatrix} \begin{pmatrix} c_{ia}\\ c_{ib} \end{pmatrix}=0 \Longrightarrow \begin{pmatrix} \varepsilon_H-\varepsilon_i & \gamma-\varepsilon_i S\\ \gamma-\varepsilon_i S & \varepsilon_H-\varepsilon_i \end{pmatrix} \begin{pmatrix} c_{ia}\\ c_{ib} \end{pmatrix}=0\end{split}\]

que tiene solución no trivial tan sólo si el determinante secular es no nulo, lo que permite encontrar los niveles de energía,

(263)\[\begin{split}\begin{vmatrix} \varepsilon_H-\varepsilon_i & \gamma-\varepsilon_i S\\ \gamma-\varepsilon_i S & \varepsilon_H-\varepsilon_i \end{vmatrix}=0 \Rightarrow \varepsilon_H-\varepsilon_i = \pm \left(\gamma-\varepsilon_iS\right)\end{split}\]

Niveles enlazante y antienlazante

En la Fig. 150 podemos observar, de forma cualitativa la posición de los dos niveles solución de la ecuación de Hartree-Fock.

Fig. 150 Esquema cualitativo de las posiciones de los niveles del ión molecular \(H_2^+\) (despreciando el solape entre los orbitales). Se puede observar que hay un nivel por encima de la energía cuasiatómica \(\varepsilon_H\) y otro por debajo de la misma.

Usando las expresiones anteriores podemos expresar la energía del nivel más profundo como,

(264)\[\varepsilon_0=\frac{\varepsilon_H +\gamma}{1+S}=E_H-\frac{J+K}{1+S}+\frac{1}{R}\]

mientras que el superior es,

(265)\[\varepsilon_1=\frac{\varepsilon_H -\gamma}{1-S}=E_H-\frac{J-K}{1-S}+\frac{1}{R}\]

donde vemos que los niveles moleculares tienen como energía base la energía del orbital atómico en el átomo aislado, \(E_H\), que se ve corregido por la integrales de interacción electrón núcleo J y K y la separación entre los átomos, R.

Si ahora analizamos los autovectores de la Ec. (262) obtenemos:

(266)\[\psi_0=\frac{1}{\sqrt{2+2S}}\left(\chi_1 + \chi_2\right) \]

y,

(267)\[\psi_1=\frac{1}{\sqrt{2-2S}}\left(\chi_1 - \chi_2\right).\]

Analicemos ahora con detalle las soluciones. Para ello es importante visualizar las soluciones gráficamente. Mostramos la solución de más baja energía, \(\psi_0\), en la Fig. 151.

Fig. 151 Orbitales de hidrógeno individuales de la molécula \(H_2^+\) y su combinación lineal enlazante \(\psi_0\). Observar como la interferencia entre los orbitales atómicos refuerza la probabilidad de encontrar al electrón en la zona central entre los núcleos.

y la más alta, \(\psi_0\), en la Fig. 152,

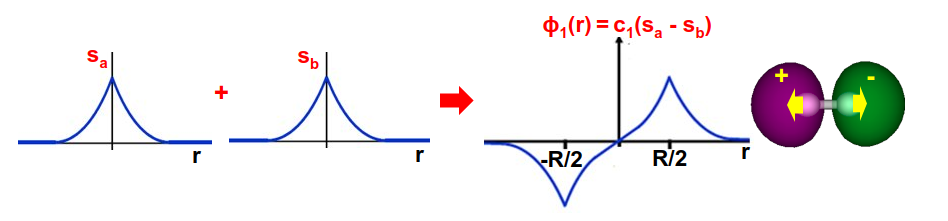
Fig. 152 Orbitales de hidrógeno individuales de la molécula \(H_2^+\) y su combinación lineal antienlazante \(\psi_1\). Observar como la interferencia entre los orbitales atómicos anula la probabilidad de encontrar al electrón en la zona central entre los núcleos.

Podemos observar que si el electrón se encuentra en el nivel \(\psi_0\) la energía es menor a la correspondiente para \(R\rightarrow \infty\) para muchos valores de R. Esto quiere decir que en esta solución los dos núcleos de hidrógeno se atraen (hasta cierta distancia de equilibrio). En cambio, en el estado \(\psi_1\) su energía es superior al límite en que los dos núcleos están infinitamente separados y no produce una situación ligada. En la Fig. 153 se muestran estas superficies de energía tanto en una base con un número mínimo de elementos, como la que estamos usando, como en una más extendida y que permite acercarse más al límite variacional.

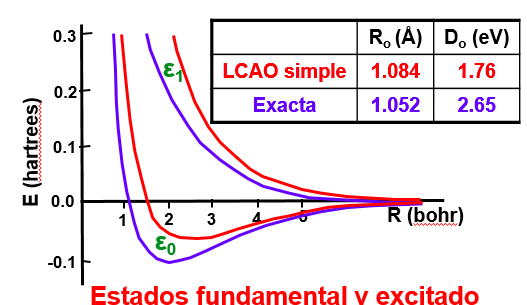
Fig. 153 Superficies de energía para la molécula \(H_2^+\). Se representan el nivel enlazante (\(\varepsilon_0\)) y el antienlazante (\(\varepsilon_1\)) para una base sencilla LCAO (en rojo) y para otra más completa (en azul) más realista desde el punto de vista de la energía de enlace que aporta.

Por estos motivos al nivel \(\psi_0\) se le denomina enlazante (los núcleos están enlazados) y al \(\psi_1\) se le denomina antienlazante. Intentemos ahora comprender que factores físicos hacen que en el nivel inferior los núcleos se atraigan y por qué en el superior se repelen. Hay 3 factores principales:

• Interacción núcleo-núcleo: Dado que los núcleos son partículas cargadas positivamente se repelen entre sí y esta repulsión debe ser compensada por como se sitúa el electrón dentro de la molécula.

• Interacción electrón-núcleo: Dependiendo de la colocación del electrón este puede hacer que los núcleos se atraigan entre sí o favorezca su repulsión. Si observamos el orbital enlazante en la Fig. 151 vemos que la interferencia entre los dos orbitales de hidrógeno es constructiva (ver signo mas en la Ec. (266))en la zona intermedia entre los núcleos. Esto refuerza la probabilidad de encontrar al electrón entre los núcleos y favorece que estos se acerquen el uno al otro (¡realmente se acercan al electrón que se coloca entre ellos!). Ver la Fig. 154.

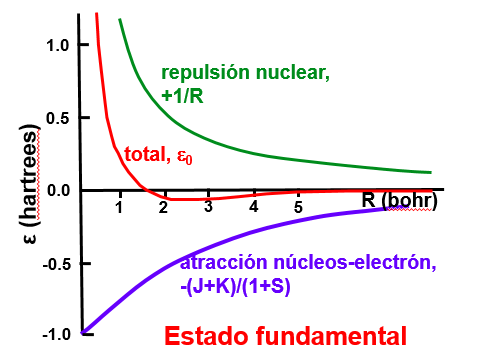
Fig. 154 Evolución de la energía electrón-núcleo y núcleo-núcleo en el ión \(H_2^+\) en función de la distancia entre núcleos R.

En el caso del orbital antienlazante (Fig. 152) la probabilidad de encontrar al electrón en el punto medio entre los núcleos es cero, debido a la interferencia destructiva entre los dos orbitales (ver signo menos en la Ec. (267)) eso hace que el electrón tienda a colocarse más cerca de los núcleos y la repulsión entre ellos aumente. Ver la Fig. 154.

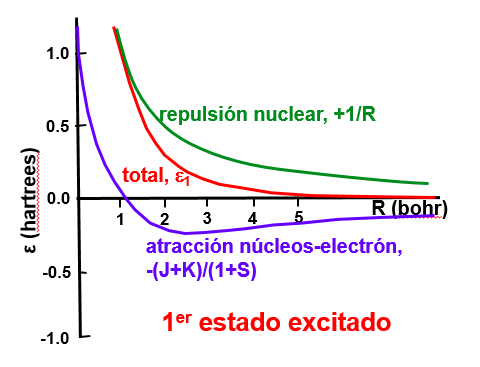
Fig. 155 El diagrama de niveles de la molécula de H\(_2\) neutra.

• Energía cinética: La energía cinética es una medida de la curvatura de la función de onda (es un operador proporcional a la segunda derivada con la posición). Una función de onda tiene asociada una energía cinética más alta cuantos más nodos tenga. Podemos ver que la región de interferencia constructiva entre los núcleos en \(\psi_0\) suaviza la curvatura de la función de onda, lo que hace que tenga menos energía cinética que \(\psi_1\) donde aparece un nodo. Por tanto, la función enlazante también tiene menos energía cinética (que es positiva) que la antienlazante, reduciendo su energía total.

Estas conclusiones las podemos ver en los cálculos Hartree-Fock mostrados en la Fig. 156 donde vemos que, para el estado \(\psi_0\), la energía cinética se reduce mucho cuando los átomos están lejos uno del otro y cuando están más cerca la energía potencial (dominada por la energía potencial electrón-núcleo) se reduce también, siendo estos los dos factores principales para crear el enlace químico.

Fig. 156 Descomposición de la energía electrónica de la molécula de H\(_2^+\) en cinética y potencial dependiendo de la separación entre los núcleos R.

Cuando los dos núcleos están suficientemente cerca la repulsión entre núcleos domina ambas contribuciones enlazantes (energía cinética y electrón núcleo) y la curva de energía se vuelve repulsiva. En un punto intermedio se produce un mínimo de la APES que es la distancia de equilibrio de la molécula. Los niveles de energía nucleares se deben de resolver utilizando como energía potencial la superficie \(\varepsilon_0\) (o \(\varepsilon_1\)) tal y como se muestra en la Fig. 157.

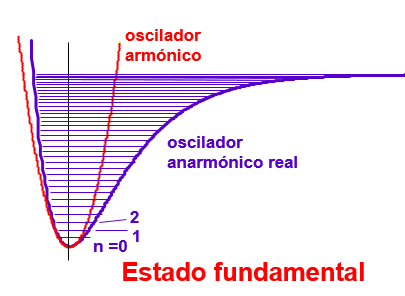
Fig. 157 Ilustración de la superficie de energía de la molécula de hidrógeno y sus niveles cuánticos calculados según la aproximación armónica.

En esta sección hemos visto como en el caso del ion \(H_2^+\) se forma el enlace químico debido a que los núcleos comparten electrones favoreciendo que se coloquen en una posición intermedia entre ellos. A este enlace donde los electrones se comparten entre los núcleos se le denomina enlace covalente.

Problemas y ejemplos