Vibraciones moleculares

Para llegar a las rotaciones moleculares o las traslaciones, retringimos los movimientos de la molécula para que no se deforme, de modo que estos se corresponden con el cambio de las coordenadas del centro de masa de la molécula y las rotaciones asociadas a los ejes cartesianos de la molécula. Para representar las distorsiones de la molécula (vibraciones) vamos a usar los llamados modos normales de la molécula. Para ello vamos a empezar observando la superficie de energía cerca del mínimo, primero en una molécula diatómica y, más tarde, en una poliatómica, para ver como extraer las diferentes formas en que podemos hacer estar deformaciones.

Aproximación cuadrática a la superficie de energía

Supongamos una molécula diatómica. Su superficie de energía, \(E_i\), tan sólo depende de la distancia interatómica, R, y tiene una forma típica como la indicada en la Fig. 216.

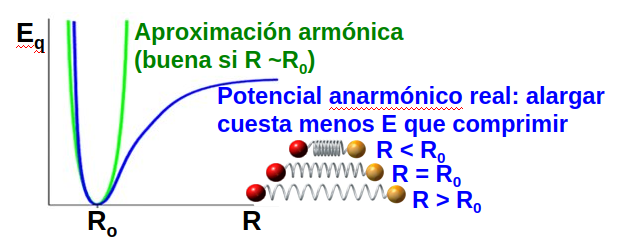
Fig. 216 Ilustración de una curva típica de disociación de una molécula diatómica (curva azul). En verde se muestra la aproximación cuadrática al mínimo. Se puede observar que en la aproximación armónica la compresión y la expansión de la molecúla son igualmente costosas desde el punto de vista energético. En cambio, en el caso real, comprimir el enlace implica un incremento de energía mucho mayor que una expansión.

Resolver el problema cuántico nuclear,

(330)\[\left(\hat{T}_n + E_i(R)\right)\Psi_n^{\alpha}=E_{i,\alpha}\Psi_n^{\alpha}\]

asociado a esta superficie es, en general, analíticamente imposible de hacer. En cambio, si la molécula se mantiene cerca de su mínimo, \(R_0\), podemos esperar que podamos aproximar la superficie de energía por una parábola. Esta parábola vendrá caracterizada por una constante de fuerza K,

(331)\[ K=\left.\frac{d^2 E}{d R^2}\right\vert_{R_0}\]

si esta constante de fuerza es grande la energía crece rápidamente con la distorsión, mientras que si es pequeña la superficie de energía será mucho más plana, como está ilustrado en la Fig. 217.

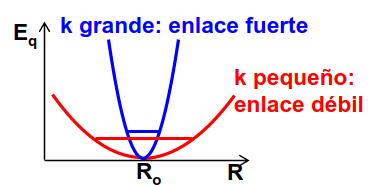
Fig. 217 Dependiendo de la curvatura del potencial la frecuencia de vibración (\(\omega=\sqrt{K/M}\)) será más rápida o lenta. Esta curvatura representa la fuerza del enlace.

Veamos ahora, por ejemplo, el cambio de coordenadas que hay que introducir en una molécula diatómica heteronuclear para obtener la separación del mismo en coordenadas del centro de masa y movimiento relativo de los átomos. Por simplicidad vamos a suponer que cada uno de los átomos tan sólo puede moverse a lo largo del eje z y que las coordenadas de cada uno se representan mediante las letras \(Z_1\) y \(Z_2\). Si \(R_0\) es la distancia de equilibrio de la molécula, su Hamiltoniano nuclear es,

(332)\[\hat{H}=-\frac{\hbar^2}{2M_1}\frac{\partial^2}{\partial Z_1^2} - \frac{\hbar^2}{2M_2}\frac{\partial^2}{\partial Z_2^2} +\frac{1}{2} K (Z_1 - Z_2 -R_0)^2 \]

Si ahora cambiamos a las coordenadas,

(333)\[Z_{CM}=\frac{M_1 Z_1+M_2 Z_2}{M_1+M_2}\]

y,

(334)\[R=Z_1-Z_2.\]

Utilizando la regla de la cadena tenemos que la derivada en \(Z_1\) es,

(335)\[\frac{\partial }{\partial Z_1} = \frac{\partial Z_{CM}}{\partial Z_1} \frac{\partial}{\partial Z_{CM}}+\frac{\partial R}{\partial Z_1} \frac{\partial}{\partial R}\]

y podemos encontrar una ecuación similar para \(Z_2\). Sustituyendo en el Hamiltoniano tenemos,

(336)\[\hat{H}=- \frac{\hbar^2}{2(M_1+M_2)}\frac{\partial^2}{\partial R_{CM}^2} -\frac{\hbar^2}{2\mu}\frac{\partial^2}{\partial R^2} +\frac{1}{2} K (R -R_0)^2 \]

donde \(\mu\) es la masa efectiva,

(337)\[\mu=\frac{M_1M_2}{M_1+M_2}.\]

Esta transformación, para una molécula general, es difícil de visualizar, por lo que explicaremos una manera de encontrar, de forma sistemática, como hacer el cambio de coordenadas. En la Ec.(336) podemos ver que el primer término se corresponde con la energía cinética de las traslaciones mientras que los otros dos se corresponden con la energía de un oscilador cuántico centrado alrededor de \(R=R_0\).

El oscilador armónico cuántico

Si ahora queremos encontrar los niveles de energía asociados a la pequeña distorsión alrededor del punto de equilibrio tenemos que tenemos que resolver el problema del oscilador armónico cuántico, asociado a una energía cuadrática con la distorsión,

(338)\[\left(-\frac{\hbar^2}{2m} \frac{d^2}{dx^2} +\frac{1}{2} K x^2\right) \chi_\nu= E_\alpha \chi_\nu\]

donde la frecuencia del oscilador es,

(339)\[\omega = \sqrt{\frac{K}{m}}\]

y sus niveles de energía, que dependen de esta frecuencia son,

(340)\[E_\nu = \left(\nu+\frac{1}{2}\right) \hbar \omega, \nu=0, 1, 2, \cdots\]

mientras que sus funciones de onda (ver Fig. 218) son,

(341)\[\chi_\nu = C_\nu H_{\nu}(y)e^{-y^2/2}, y=\sqrt{\frac{\omega}{\hbar}}.\]

donde \(H_\nu\) son los polinomios de Hermite. Es decir, que esperamos que los niveles vibracionales de una molécula estén, aproximadamente, igualmente espaciados, por lo que habrá una absorción típica asociada a una energía \(\hbar\omega\).

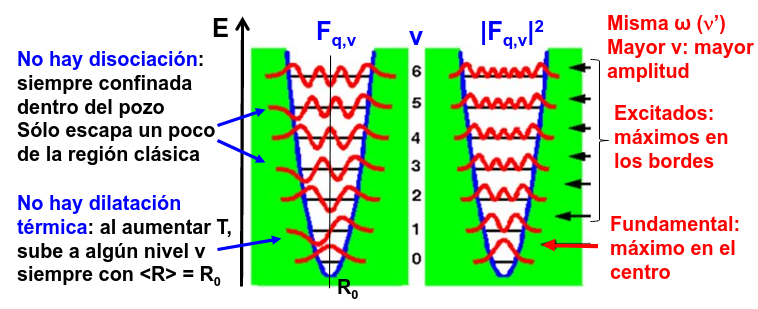
Fig. 218 Ilustración de la solución de un oscilador armónico cuántico. A la derecha se muestra la función de onda, \(F_{q,\nu}\) del niveles q y frecuencia \(\nu\), y, a la derecha, su densidad de probabilidad asociada.

Moléculas poliatómicas

En el caso de las moléculas poliatómicas debemos reducir los 3N-6 grados de libertad vibracionales (3N-5 en moléculas linales) a osciladores armónicos. Esto siempre se realiza del mismo modo.

• 1. Se definen las coordenadas pesadas por la masa, \(\tilde{R}_{\alpha^\prime}\),

(342)\[\tilde{R}_{\alpha^\prime}=\sqrt{M_{\alpha^\prime}} R_{\alpha^\prime}\]

lo que permite transformar la energía cinética del siguiente modo,

(343)\[\hat{T}_n = -\sum_{\alpha^\prime} \frac{\hbar^2}{2M_\alpha^\prime} \frac{d^2}{dR^2_{\alpha^\prime}} \Rightarrow \hat{T}_n = -\sum_{\alpha^\prime} \frac{\hbar^2}{2} \frac{d^2}{d\tilde{R}^2_{\alpha^\prime}}\]

Esto permite evitar tener que tener en cuenta las masas en la energía cinética, como se muestra en la ecuación anterior.

• 2. Se expande la superficie de energía alrededor del mínimo hasta segundo orden en las coordenadas pesadas por la masa,

(344)\[E_{i}(\{\tilde{R}\})\approx E_{i}(\tilde{R}_0)+\sum_{\alpha^\prime} 0 \tilde{R}_\alpha^\prime + \frac{1}{2}\sum_{\alpha^\prime,\beta^\prime} \left.\frac{d^2 E_i}{d\tilde{R}_{\alpha^\prime} d\tilde{R}_{\beta^\prime}} \right\vert_{R=R_0}\tilde{R}_{\alpha^\prime} \tilde{R}_{\beta^\prime} + \cdots\]

comparando la Ec. (330) con la Ec. (344) observamos que, en vez de la constante del muelle K, tenemos el Hessiano de la superficie de energía,

(345)\[\mathcal{H}=\frac{1}{2} \left. \frac{d^2 E_i}{d\tilde{R}_{\alpha^\prime} d\tilde{R}_{\beta^\prime}} \right\vert_{R=R_0} \]

que es una matriz. Diagonalizando esta matriz podemos encontrar los modos normales, las vibraciones que son independientes unas de otras y que transforman la ecuación del movimiento vibracional en una suma sencilla de modos (sin acoplamientros cruzados). En particular, la ecuación de autovalores es y los autovectores asociados son,

(346)\[ \mathcal{H}Q_\alpha = K_\alpha Q_\alpha \rightarrow Q_\alpha = \sum_{\alpha^\prime} c_{\alpha \alpha^\prime} \tilde{R}_{\alpha^\prime}\]

donde \(c_{\alpha\alpha^\prime}\) son los autovectores del Hessiano. Es decir, cuando lo aplicamos sobre la ecuación del movimiento nuclear, sustituyendo (346) en la energía cinética nuclear, Eq. (343) y el potencial, Ec. (344) obtenemos,

(347)\[ \left(\hat{T}_n + E_i(\{\vec{R}\})\right)\Psi_n^{\gamma}\approx \sum_{\alpha} \left(\frac{\hbar^2}{2} \frac{d^2}{dQ_\alpha^2}+\frac{1}{2}K_\alpha Q_\alpha^2\right)\Psi_n^{\gamma} = E_{i,\gamma}\Psi_n^{\gamma}\]

donde podemos observar que el Hamiltoniano es ahora una suma en \(\alpha\) de los modos normales de vibración. Dado que cada modo es independiente entre sí, y lo es también a los movimientos de traslación y rotación, la función de onda total asociada a los núcleos de la molécula es,

(348)\[\Psi_n^{\gamma}=\chi_\text{tras}(x,y,z) \chi_\text{rot} (\alpha,\beta,\gamma)\prod_{\alpha}^{3N-6} \chi_\alpha (Q_\alpha)\]

Cada uno de estos modos normales es un oscilador armónico cuántico. Por lo tanto, debemos esperar que una molécula no lineal tenga 3N-6 frecuencias características de sus vibraciones (ver más abajo para el ejemplo del CO\(_2\)). Aún así, la simetría puede reducir el número de frecuencias diferentes que presente una molécula ya que habrá modos vibracionales que sean equivalentes (modos degenerados).

Ejemplo

Para ver como se obtienen las vibraciones de una molécula tomemos, por ejemplo, la molécula de CO\(_2\). En la aproximación armónica podemos considerar cada enlace como un muelle. Los enlaces son más duros en las direcciones interatómicas y cuanto más cerca están los átomos (ver Fig. 219). Por tanto, si consideramos movimientos en los que las distancias interatómicas cambian (en vez de los ángulos), tendremos los modos de estiramiento (stretching en inglés) de una molécula. En este caso ocurren a lo largo del eje z.

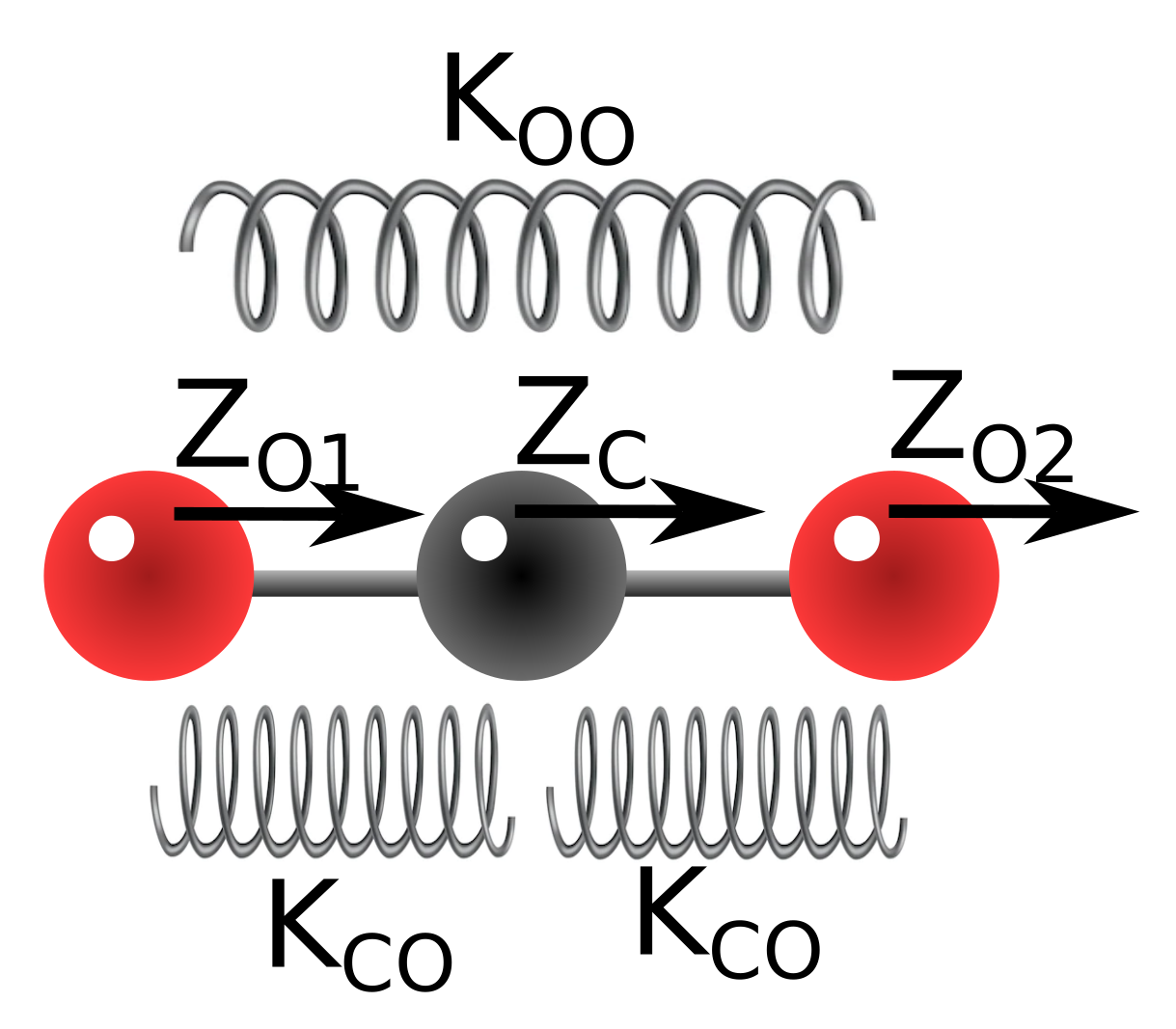
Fig. 219 Interacciones elásticas en la molécula de CO\(_2\) cuando los átomos sólo pueden moverse a lo largo del eje z. Cada interacción se representa mediante un muelle, por lo que tenemos 3 de ellas, una entre los oxígenos, con constante de fuerza K\(_{OO}\), y dos, que son iguales, entre el carbono central y los oxígenos laterales, \(K\)_{CO}$. Dado que la distancia entre átomos es más pequeña en esta última esperamos que esa interacción sea más fuerte que la existente entre los oxígenos.

Para resolver el problemas vibracional primero, hacemos la transformación a coordenadas pesadas por la masa,

(349)\[\begin{split}\vec{\tilde{Z}}^T=M^{1/2}\vec{Z}^T \rightarrow \begin{pmatrix} \tilde{Z}_{O_1} \\ \tilde{Z}_C\\ \tilde{Z}_{O_2}\end{pmatrix} = \begin{pmatrix} \sqrt{M_O} & 0 & 0 \\ 0 & \sqrt{M_C} & 0 \\ 0 & 0 & \sqrt{M_O} \end{pmatrix}\begin{pmatrix} Z_{O_1} \\ Z_C\\ Z_{O_2}\end{pmatrix}\end{split}\]

En este punto el Hamiltoniano es,

(350)\[\hat{H}=-\frac{\hbar^2}{2}\frac{\partial^2 }{\partial \tilde{Z}_{O_1}^2}-\frac{\hbar^2}{2}\frac{\partial^2 }{\partial \tilde{Z}_{O_2}^2}-\frac{\hbar^2}{2}\frac{\partial^2 }{\partial \tilde{Z}_{C}^2}+\frac{1}{2}\vec{\tilde{Z}} \tilde{\mathcal{H}}\vec{\tilde{Z}}^T\]

Segundo, escribimos la matriz de constantes de fuerza para los movimientos a lo largo del eje z de los átomos de la molécula de CO\(_2\),

(351)\[\begin{split}\mathcal{K}=\frac{\partial^2 E_i}{\partial Z_i \partial Z_j} = \begin{pmatrix} K_{CO}+K_{OO} & -K_{CO} & -K_{OO} \\ -K_{CO} & 2K_{CO} & -K_{CO} \\ -K_{OO} & -K_{CO} & K_{CO} + K_{OO} \end{pmatrix}\end{split}\]

De esto obtenemos, la matriz Hessiana, \(\tilde{\mathcal{H}}\), pasando a coordenadas pesadas por la masa,

(352)\[\begin{split}\mathcal{H}=\frac{\partial^2 E_i}{\partial \tilde{Z}_i \partial \tilde{Z}_j} = \frac{1}{\sqrt{M_i M_j}} \frac{\partial^2 E_i}{\partial Z_i \partial Z_j} = \begin{pmatrix} (K_{CO}+K_{OO})/M_O & -K_{CO}/\sqrt{M_O M_C} & -K_{OO}/M_O \\ -K_{CO}\sqrt{M_O M_C} & 2K_{CO}/M_C & -K_{CO}\sqrt{M_O M_C} \\ -K_{OO}/M_O & -K_{CO}\sqrt{M_O M_C} & (K_{CO} + K_{OO})/M_O \end{pmatrix}\end{split}\]

Diagonalizando esta matriz obtenemos 3 autovalores (y autovectores) que representamos en la Fig. 220.

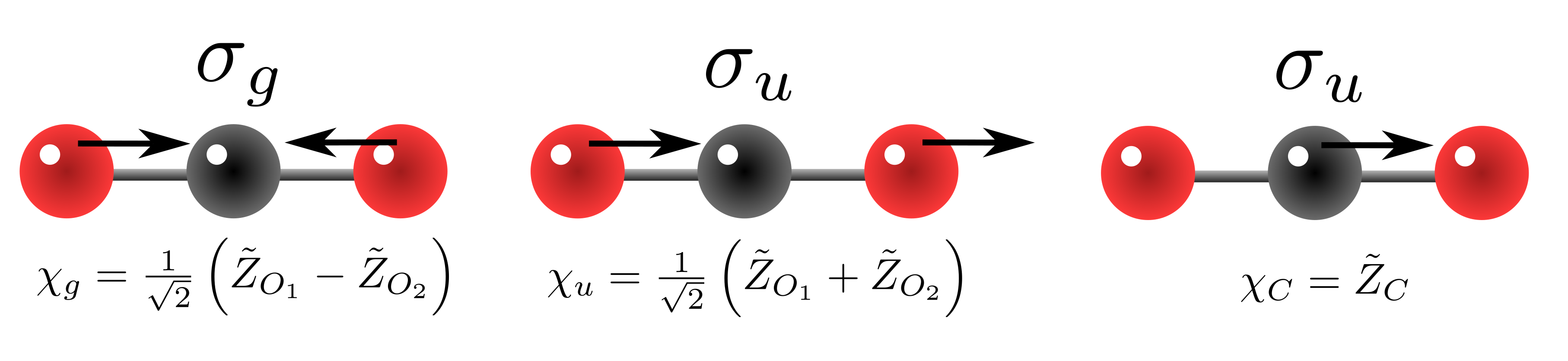
Fig. 220 Componentes simetrizadas de las vibraciones a lo largo del eje z del CO\(_2\) incluyendo un modo par debido al movimiento respiratorio de los oxígenos y dos modos impares asociados al movimiento de los oxígenos y del carbono.

Aquí podemos ver que hay 3 modos de tipo (\(\sigma\), de stretching), dos de ellos son impares (invertiendo la molécula cambian de signo) y 1 par (que se mantiene invariante cuando invertimos la molécula). Con estos autovectores el Hessiano se diagonaliza (último término en la Ec. (350)), con lo que obtenemos el Hamiltoniano,

(353)\[\hat{H}=-\frac{\hbar^2}{2}\frac{\partial^2 }{\partial \tilde{Q}_{u1}^2}-\frac{\hbar^2}{2}\frac{\partial^2 }{\partial \tilde{Q}_{u2}^2}-\frac{\hbar^2}{2}\frac{\partial^2 }{\partial \tilde{Q}_{g}^2}+\frac{1}{2}\omega_g^2 Q_g^2+\frac{1}{2}\omega_{u1}^2 Q_{u1}^2+\frac{1}{2}\omega_g^2 Q_{u2}^2\]

que, como podemos observar, está separado en osciladores armónicos independientes. Las frecuencias de estos son,

(354)\[\begin{split} \omega_g^2 = \sqrt{2} \frac{K_{CO}+K_{OO}}{M_O} \\ \omega_{u1}^2 = 0 \\ \omega_{u2}^2 = \left(\frac{1}{M_O} + 2\frac{1}{M_C}\right)K_{CO}\end{split}\]

dado que esperamos que \(K_{CO}>K_{OO}\) debido a que los átomos de carbono y oxígeno están a una distancia más pequeña que los oxígenos entre sí la predicción que podemos hacer es que el modo par es de mayor frecuencia en esta molécula.

Anarmonicicdad

Aunque la aproximación armónica funciona muy bien a baja temperatura y con enlaces fuertes, no es capaz de explicar muchos fenómenos, como la expansión de los materiales cuando sube la temperatura. Esta es debida a que, según los enlaces se van estirando, se vuelven cada vez más débiles, tal y como se muestra en la Fig. 216. No hay una manera general de representar estas curvas anarmónicas, aunque a lo largo de la historia ha habido algunas propuestas que, de forma aproximada, funcionan bien. Una de las más exitosas para moléculas diatómicas es el potencial de Morse,

(355)\[E=D\left[1-e^{-a(R-R_0)}\right]\]

donde \(D\) es la energía de disociación de la molécula, es decir, la energía necesaria para romper el enlace entre los dos átomos completamente, y el parámetro \(a\) mide cuanto de rápido tiende el sistema de su mínimo a la disociación. En Fig. 221 podemos ver que, cuando un enlace se comprime desde su posición de equilibrio, \(R_0\), su energía crece rápidamente, mientras que cuando se estira esta crece más lentamente mientras su enlace se debilita hasta la disociación.

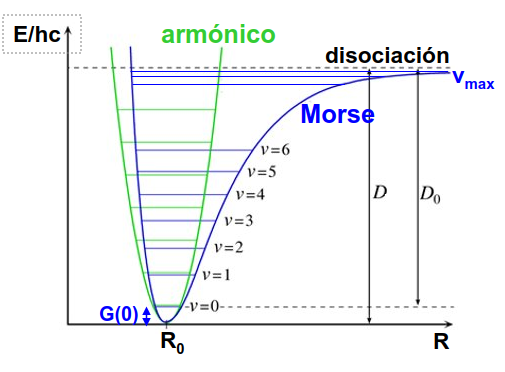
Fig. 221 Comparación de un potencial armónico (en verde) con un potencial de Morse (en azul) incluyendo los niveles cuánticos (en negro) típicos de este último potencial . Como puede observarse la distancia entre niveles se acorta hasta llegar al continuo por encima de la energía de disociación.```

A parte de reproducir cualitativamente lo que esperamos de este tipo de curva una de las ventajas que tiene el potencial de Morse es que la ecuación de Schrödinger asociada al mismo puede ser resuelta analíticamente, dando lugar a la solución,

(356)\[E_\nu=-\frac{a^2\hbar^2}{2m}\left(\lambda-\nu-\frac{1}{2}\right)^2, \lambda=\frac{\sqrt{2mD}}{a\hbar}\]

donde \(\nu\) es el número cuántico vibracional. Aquí, Fig. 221, podemos ver que según subimos desde el estado fundamental \(\nu=0\) los niveles vibracionales están cada vez más pegados hasta que, por encima de la energía de disociación, se llega a un continuo.

Según la temperatura crece los niveles con \(\nu\) más grande se van poblando, lo que significa que el punto medio de la vibración se desplaza hacia valores de R más grandes, lo que también explica la expansión térmica de los materiales.

Problems and solution examples