Cadena monoátomica

En la sección previa veíamos que, a través de las ecuaciones clásicas del movimiento de los átomos de un sólido, podíamos calcular sus modos normales de vibración resolviendo la siguiente ecuación,

(411)\[K_k\vec{\epsilon}= M\omega_k^2 \vec{\epsilon}.\]

Aquí vamos a trabajar con el primer ejemplo concreto, la cadena monoatómica, que se muestra en la Fig. 236. En vez de aplicar la Ec. (411) directamente, retrazaremos nuestros pasos para ver como surgen los diferentes términos en detalle.

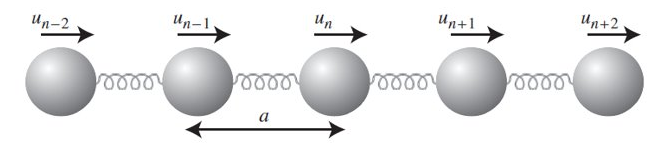
Fig. 236 Ilustración de la cadena monoatómica con interacciones a primeros vecinos. el desplazamiento de cada átomo respecto a a su posición de equilibrio lo llammos \(\u_n\) donde n es la celda de la red de Bravais donde se encuentra el átomo.```

Energía elástica

El primer paso en nuestra construcción era el cálculo de la energía elástica vibracional de la cadena. Para ello primero debemos estudiar la estructura del sistema.

La cadena mostrada en la Fig. 236 se trata de una red de Bravais unidimensional, que suponemos que se extiende a lo largo del eje z, y que tiene un único átomo de motivo que se encuentra en la posición \(\vec{\tau}=[0.0]\). Por tanto, podemos nombrar los desplazamientos de los átomos \(\vec{u}(n)\) utilizando un único índice, \(n\), que indica la celda donde se encuentra el átomo. En esta primera resolución supondremos que el movimiento de los átomos está restringido a la dirección de la cadena, el eje z, por lo que \(\vec{u}_n=u(n) \vec{u}_z\).

Si, como se muestra en la Fig. 236, cada átomo interacciona, tan sólo, con sus primeros vecinos, vemos que podemos asignar a cada celda un único muelle. Dado que la energía total es la suma a todas las celdas de los muelles que están en una de estas celdas, tenemos,

(412)\[ U=\sum_n \frac{1}{2} K \left[u(n)-u(n+1)\right]^2.\]

Ecuación del movimiento

Una vez conocida podemos calcular la ecuación del movimiento. Tal y como se comentaba en la sección modos normales todos los átomos equivalentes del sólido deben tener una ecuación del movimiento equivalente, por lo que nos centramos tan sólo en el átomo en la celda n del sólido y escribimos su ecuación de Newton,

(413)\[ m\vec{a}=\vec{F}\rightarrow M\ddot{u}(n)=-\frac{\partial U}{\partial u(n)}=-K\left[2u(n)-u(n-1)-u(n+1)\right]\]

donde hemos tenido cuidad al expandir el sumatorio para observar en que términos del mismo (el n y el n-1) aparecía la coordenada \(u(n)\).

Solución de la ecuación del movimiento

Ahora introducimos la solución de la ecuación de movimiento como una combinación de movimientos armónicos de los átomos de la red, teniendo cuidado que todos los átomos equivalentes tienen que tener una misma amplitud. Además conocemos que la solución debe respetar la simetría traslacional del sólido, mediante el teorema de Bloch, con lo que probamos con la solución,

(414)\[u(n)=\epsilon e^{i(kna-\omega_k t)}\]

donde observamos que, dado que tan sólo tenemos un átomo que se mueve en un dirección (un único grado de libertad en la celda unidad), la amplitud, en vez de ser un vector, es un escalar. Calculamos ahora la aceleración de los átomos con esta solución,

(415)\[\ddot{u}(n)=-\epsilon \omega_k^2 e^{i(kna-\omega_k t)}\]

Sustituyendo las Ecs. vs_vib_bloch y (415) en la ecuación de movimiento, Ec. (413), obtenemos,

(416)\[M\varepsilon\omega_k^2=\left(2K-Ke^{-ika}-Ke^{ika}\right)\varepsilon\]

que es, precisamente, la Ec. (411), obtenida anteriormente. Aquí podemos identificar la matriz de constantes de fuerza en el espacio recíproco,

(417)\[K_k = \sum_{\Delta n} K_{\Delta n} e^{ik \Delta n a} =-\underbrace{Ke^{-ika}}_{n=-1}+\underbrace{2Ke^{ik0a}}_{n=0}-\underbrace{Ke^{ika}}_{n=1}=K\left(2-2\cos ka\right)=2K\left(1-\cos ka\right)\]

donde la suma se extiende a todas las interacciones de uno de los átomos de la cadena.

De la ecuación, Ec. (416) podemos extraer las frecuencias,

(418)\[\omega_k^2=2\frac{K}{M}\left(1-\cos ka\right)\]

Si representamos esta solución en función de k, tomando valores dentro de la primera zona de Brillouin,

(419)\[k\in\left(-\frac{\pi}{a},\frac{\pi}{a}\right),\]

tenemos la curva de dispersión mostrada en la gráfica, Fig. 237.

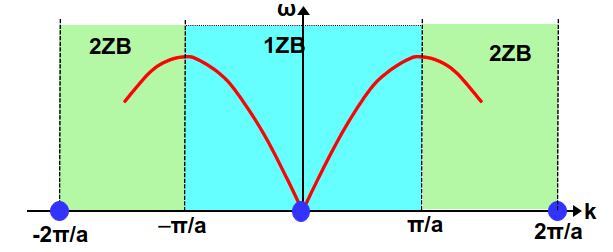
Fig. 237 Forma de la banda vibracional de la cadena monoatómica, donde en el eje x se representa el vector de ondas y en el eje y la frecuencia \(omega_k\), que es proporcional a la energía de vibración del modo k. En un transfondo oscuro se muestra la primera zona de Brillouin, que es la región del espacio recíproco donde la solución es única (en un transfondo más claro se muestra la segunda zona de Brillouin donde la solución se repite).

Interpretación y visualización de los modos

Veamos ahora que forma tienen los modos, lo que nos permitirá entender la forma de la Fig. 237. Para ello es necesario utilizar el teorema de Bloch que nos permite calcular como se mueven dos átomos consecutivos de un sólido,

(420)\[ T_a u(n)=u(n+1)=\epsilon e^{i(k(n+1)a+\omega_kt)} = e^{ika}\epsilon e^{i(kna+\omega_kt)}=e^{ika} u(n)\]

Veamos ahora que ocurre cuando damos diferentes valores a k:

-Caso 1 - Centro de zona \(k=0\): En el centro de zona la Ec. (420) nos informa de que un átomo y el siguiente de la cadena se mueven en fase:

(421)\[ T_a u(n)=u(n+1)=e^{i0\cdot a} u(n)=u(n)\]

Como se puede ver en la Fig. 238 los átomos se mueven acompasadamente y por lo tanto su separación relativa no cambia. Eso significa que los muelles no se comprimen y no almacenan energía. Efectivamente, podemos observar que la frecuencia de vibración para k=0 es cero. Esto es una propiedad general de los niveles con \(\omega=0\) que ocurren a k=0 en todos los cristales.

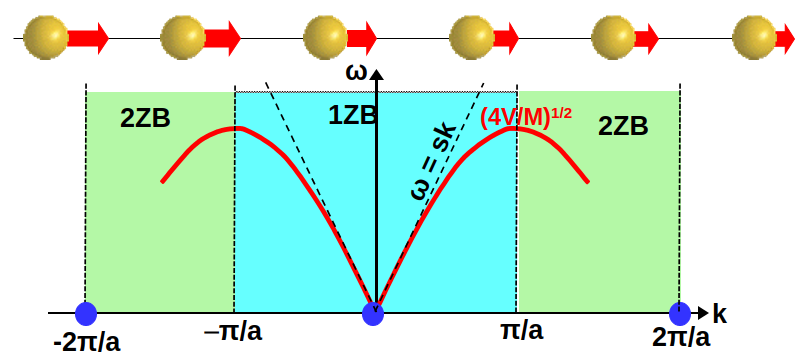
Fig. 238 Ilustración de los modos normales cerca de k=0 donde la longitud de onda es muy grande, por lo que los átomos se mueven en fase y su separación varía muy poco. La pendiente de la curva de dispersión indica la velocidad del sonido en el sólido.

Podemos ver que cuando k es pequeño la frecuencia crece linealmente con el vector de ondas. Como sabemos, la velocidad de grupo de una onda se define, precisamente, como,

(422)\[s=v_k=\frac{d\omega_k}{dk}\]

y representa la velocidad a la que se mueve el sonido (que es una onda asociada a la vibración de los átomos del sistema) en el sólido. Calculando este valor para nuestra expresión de la frecuencia obtenemos,

(423)\[s=a\sqrt{\frac{K}{M}}\cos\frac{ka}{2}\rightarrow \omega_k \approx s k \rightarrow s(k=0)=a\sqrt{\frac{K}{M}}\]

donde vemos que la velocidad del sónido crece con el parámetro de malla (cuidado porque, normalmente, los enlaces se vuelven más débiles con el mismo), la fuerza del enlace dada por la constante de fuerza K y la masa de los átomos de la cadena.

-Caso 2 - Borde de zona \(k=\pm \pi/a\): En el centro de zona la Ec. (420) muestra que un átomo y el siguiente de la cadena se mueven en contrafase:

(424)\[ T_a u(n)=u(n+1)=e^{i \frac{\pi}{a}\cdot a} u(n)=-u(n)\]

Esto es lo que se puede ver en la Fig. 239 donde los átomos se acercan y alejan entre sí por parejas, alargando y comprimiendo los enlaces de forma máxima. Esto hace que la frecuencia de vibración asociado a este modo sea máxima dentro de este sólido.

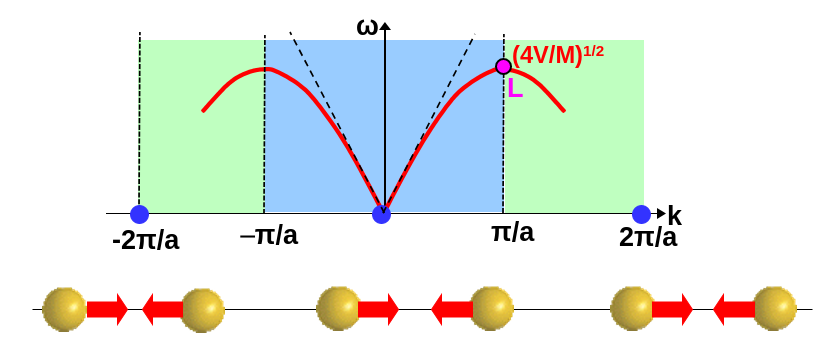
Fig. 239 Ilustración del modo normal cerca de \(k=\pm\pi/a\) en la cadena monoatómica en la que la longitud de onda es mínima, \(\lambda=2a\), y que hace que los átomos consecutivos se muevan en contrafase.

Si ahora calculamos la velocidad del sonido de esta onda, podemos ver que, como es un máximo en la curva de dispersión, su velocidad es nula,

(425)\[s=v_k=\frac{d\omega_k}{dk}=a\sqrt{\frac{K}{M}}\cos\frac{ka}{2}\rightarrow s(k=\pi/a)=0.\]

Si aplicaramos el teorema de Bloch a modos con vectores de onda intermedios obtendríamos soluciones como las que se muestran en la Fig. 240 donde la longitud de onda para de infinita para k=0 a ser mínima cuando \(k=\pi/a\).

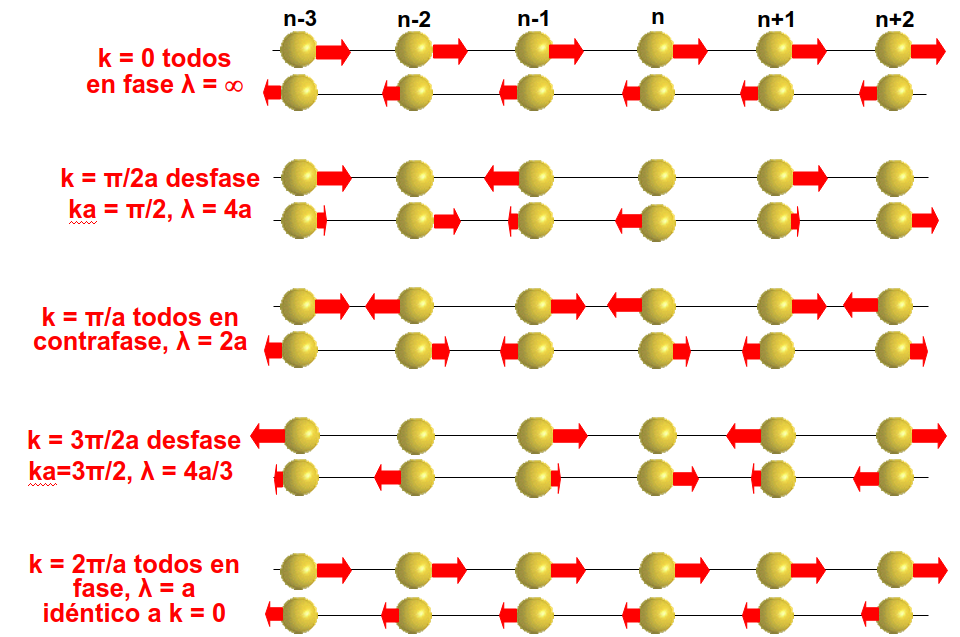
Fig. 240 Ilustración de varios modos de vibración asociados a diferentes valores del vector de onda, \(k\), en la cadena monoatómica.

Propiedades de la solución

Como indicabamos al introducir el teorema de Bloch las vibraciones (y, en general, las ondas) en un sólido están definidas de forma única en la primera zona de Brillouin. Si calculamos la frecuencia fuera de la misma (ver Fig. 241) podemos ver como las frecuencias se repiten periódicamente en la segunda, tercera, etc. zonas de Brillouin.

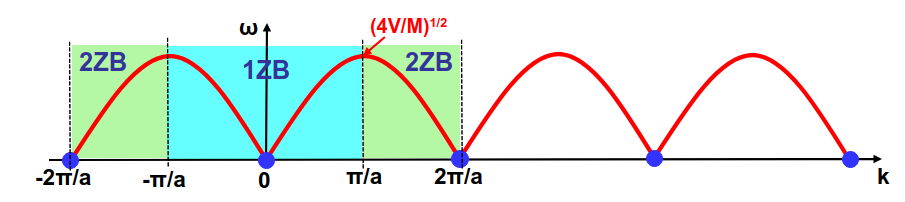
Fig. 241 Figura que ilustra como la solución de las vibraciones en la cadena monoatómica se repiten de forma periódica con el vector de ondas, \(k\).

Por otro lado, cuando el sólido se desplaza rígidamente no cambia la energía del mismo. Esto es equivalente a lo que se mostraba para las vibraciones con muy larga longitud de onda donde se comprobaba que la frecuencia era cero, es decir, que no cambia la energía con el desplazamiento. Tomando la ecuación del movimiento y trasladando todos los átomos una cantidad fija, \(d\), tenemos,

(426)\[u^\prime(n)=u(n)+d\]

Por lo tanto,

(427)\[\ddot{u}(n)=-\frac{K}{M}\left[2u(n)+2d-u(n-1)-d-u(n+1)-d\right]=-\frac{K}{M}\left[2u(n)-u(n-1)-u(n+1)\right]\]

podemos ver que la ecuación del movimiento no cambia cuando hacemos una traslación rígida del sólido.

Problems and solution examples