Rotación molecular

Cuando hacemos traslaciones o giros manteniendo la molécula en una geometría rígida, la superficie adiabática de energía, \(E_i\), sobre la que ocurre la dinámica molecular (Ec. (317)) no cambia. Mientras tanto, la energía cinética nuclear, \(T_n\), si que varía. Por lo tanto, queremos transformar el operador energía cinética nuclear a coordenadas que incluyan, por un lado, la posición del centro de masas, \(\vec{R}_{cm}\) (Ec. (318)) y, por otro lado, la rotación de la molécula a lo largo de los ejes cartesianos o los ángulos de Euler. Con esta última transformación obtenemos el rotor cuántico que se describe en la siguiente sección.

Rotor cuántico

Cambiando de coordenadas podemos extraer una parte de la energía cinética que sólo depende de la rotación de la molécula a lo largo de los ejes cartesianos. Esta contribución es,

(320)\[T_n \rightarrow T_\text{rot}=\frac{1}{2}\sum_{xy}\frac{1}{I_{xy}}\hat{J}_x \hat{J}_y \]

donde \(\hat{J}_x\) es el operador que representa el momento angular de la molécula a lo largo del eje x (donde x es x, y o z y \(\theta_x\) el ángulo de giro alrededor de estos mismos ejes).

(321)\[\hat{J}_\gamma =-i\hbar \frac{\partial}{\partial \theta_\gamma} ~~ \gamma=x,y,z\]

e \(I_{xy}\) es el tensor de inercia,

(322)\[I_{xy}=\sum_\alpha M_\alpha R_{\alpha,x} R_{\alpha,y}\]

El tensor de inercia es una matriz 3x3 cuyo valor depende de la geometría de la molécula y las masas de sus átomos. Si la diagonalizamos y transformamos el Hamiltoniano a los nuevos ejes obtenemos,

(323)\[T_\text{rot}=\frac{1}{2}\sum_{q}\frac{1}{I_{q}}\hat{J}_q^2\]

donde podemos ver que cada eje de rotación q es independiente a los otros 2.

Para discutir la solución empezamos por la cuantización del módulo del momento angular,

(324)\[\hat{J}^2 \rightarrow \hbar^2 J(J+1)\]

Si el tensor de inercia de la molécula es una matriz diagonal, el llamado rotor esférico, que se da en moléculas icosaédricas, tetraédricas u octaédricas, tenemos,

(325)\[\hat{H}=\frac{\hat{\vec{J}}^2}{2I} \rightarrow E_J=\frac{\hbar^2}{2I}J(J+1) = B J(J+1),~ J=0,1,2...\]

Por lo que podemos ver que la energía crece cuadráticamente con el momento angular, lo que es completamente análogo al caso clásico del sólido rígido donde,

(326)\[E=\frac{1}{2I}J^2\]

Si ahora calculamos la separación entre los diferentes niveles observamos,

(327)\[E_{J+1}-E_{J}=2B(J+1), J=0,1,2,\cdots\]

Es decir, crece linealmente con el momento angular total. Una representación gráfica de estos niveles y su separación viene dada en la Fig. 212.

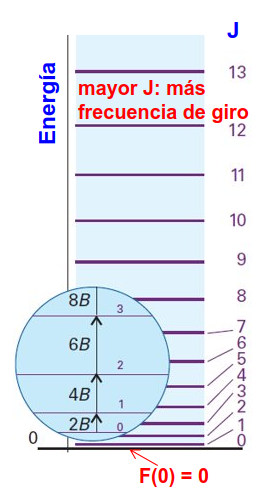
Fig. 212 Ilustración de los niveles rotacionales de un rotor esférico (que puede ser una molécula tetragonal, octaédrica o icosaédrica). A la izquierda se muestra la separación de los niveles y, a la derecha, su número cuántico, J, asociado.

Clasificación moléculas según momento de inercia

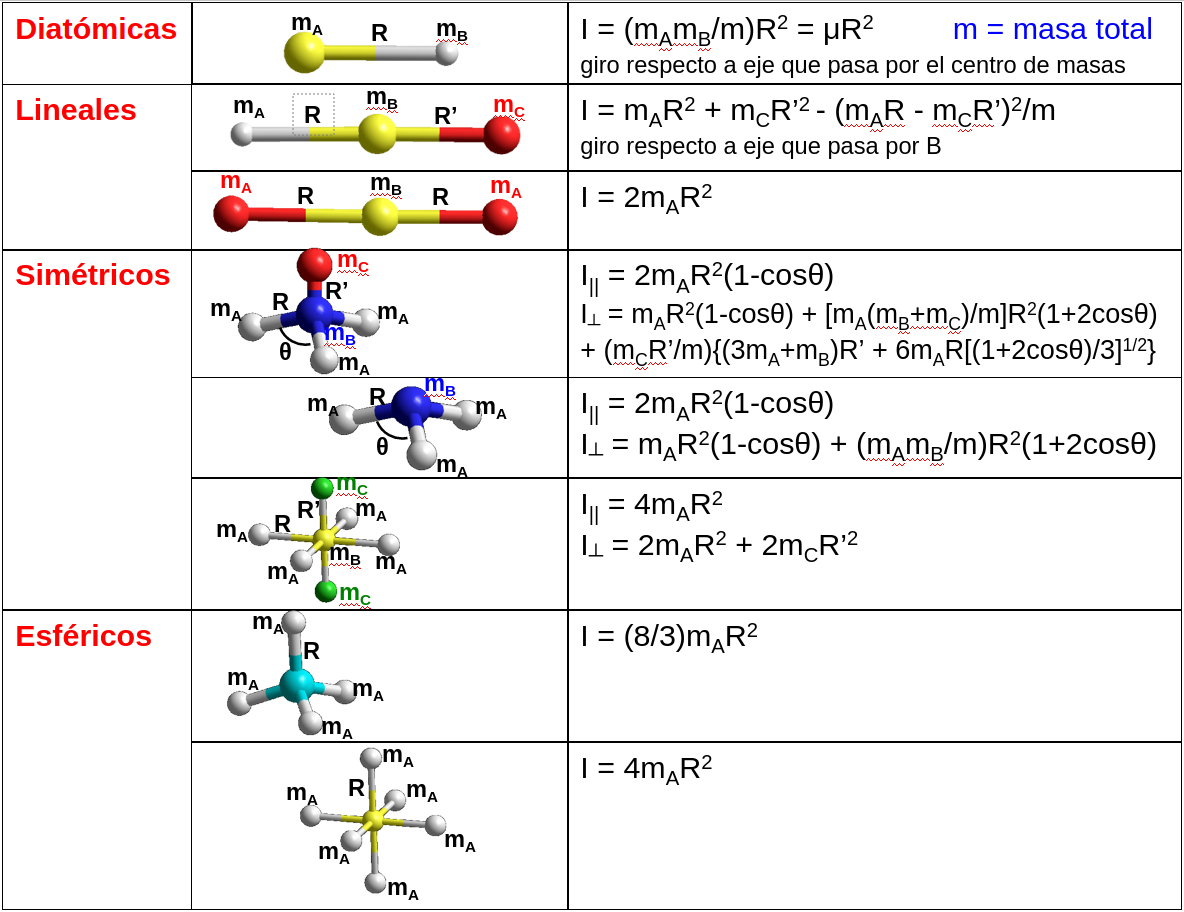
Fig. 213 Tensores de inercia para algunas molécula sencillas obtenidas a partir de sus geometrías.

Dependiendo la forma del tensor de inercia de cada molécula el tensor de inercia tiene 1, 2 o 3 valores \(I_q\) diferentes. Las moléculas no lineales con 1 sólo autovalor (triplemente degenerado) se denominan rotores esféricos, las que tienen 2 valores se llaman rotores simétricos y las que tienen 3 valores rotores asimétricos. La tabla muestra los valores de \(I_q\) para algunos casos sencillos.

Rotor simétrico

Los rotores simétricos se distinguen por tener dos tipos de ejes de rotación bien diferenciados. Por ejemplo en la figura que muestra los ejes de rotación del amoníaco, Fig. 214, podemos observar como el tensor de inercia alrededor del eje z de la molécula es diferente a las rotaciones a lo largo del eje x o y. Por ejemplo, en el primer caso el átomo de nitrógeno no giraría, dado que se encuentra sobre el eje, mientras que en los ejes x e y este átomo se encuentra a una distancia finita del centro de rotación y participa en el momento de inercia.

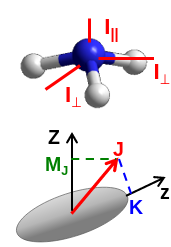
Fig. 214 Un ejemplo de rotor simétrico es la molécula de amononíaco, NH\(_3\), donde las rotaciones en el eje z y los ejes x o y muestran un momento de inercia marcadamente diferente.

En estas moléculas el Hamiltoniano rotacional es,

(328)\[\hat{H}=\frac{\hat{J}_x^2+\hat{J}_y^2}{2I_\perp}+\frac{\hat{J}_z^2}{2I_\parallel}=\frac{\hat{J}^2}{2I_\perp}+\hat{J}_z^2\left(\frac{1}{2I_\parallel}-\frac{1}{2I_\perp}\right)\]

donde, para expresar el Hamiltoniano se ha utilizado el módulo del momento angular (al cuadrado) y su proyección sobre el eje z. Si ahora cuantizamos el problema obtenemos,

(329)\[E(J,K)=J(J+1) \frac{\hbar^2}{2I_\perp}+K^2 \hbar^2 \left(\frac{1}{2I_\parallel}-\frac{1}{2I_\perp}\right)=B^\prime J(J+1)+(A^\prime-B^\prime)K^2\]

Es decir, los niveles de energía, tal y como está ilustrado en la Fig. 215, varían dependiendo de como se alinee el momento angular total con el eje z de la molécula.

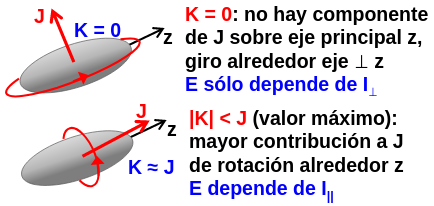
Fig. 215 Ilustración de como afectan a la rotación de una molécula de tipo rotor simétrico el moéculo de su momento angular, J, y la proyección del mismo sobre el eje z.

Problems and solution examples