Fundamentos

La forma práctica en la que utilizamos la difracción de rayos-X para observar la estructura cristalina fue propuesta por Bragg en 1913. Esencialmente, Bragg propone que los ángulos asociados a los picos de un difractograma de rayos-X en un material cristalino contienen información directa de las distancias interplanares.

Ley de Bragg

Fig. 94 Diferencia de caminos en una red \(\bar{AC}-\bar{AB}\) y su relación con la ley de Bragg

Para cuantificar esta afirmación nos fijamos en la Fig. 94 que permite observar como la diferencia de caminos entre el rayos saliente superior y el intermedio es,

(95)\[\bar{AC}-\bar{AB}=n\lambda\]

Observando que el triángulo ABC es rectángulo (el ángulo recto se encuentra en B) tenemos la siguiente relación entre el cateto \(\bar{AB}\) y la hipotenusa \(\bar{AC}\),

(96)\[\bar{AB}=\bar{AC}\cos 2\theta.\]

Por otro lado, la distancia interplanar \(d_{hkl}\) se relaciona con \(\bar{AC}\) mediante otro triángulo rectángulo,

(97)\[d_{hkl}=\bar{AC}\sin \theta\]

Sustituyendo las Ecs. (96) y (97) en la Ec. (95) se obtiene,

(98)\[\bar{AC}-\bar{AB}=\bar{AC}\left(1-\cos 2\theta\right)= \frac{d_{hkl}}{\sin \theta} 2 \sin^2\theta=n\lambda\]

Con lo cual se llega a la ley de Bragg,

(99)\[2d_{hkl}\sin\theta = n\lambda.\]

Attention

La ley de Bragg se escribe de forma alternativa del siguiente modo,

(100)\[2d_{hkl}\sin\theta = \lambda\]

donde se ha eliminado que la diferencia de caminos sea un número entero de longitudes de onda. De forma práctica lo que ocurre es que los índices de Miller al usar la Ec. (100) ahora pueden contener un factor común (que es el entero n).

Ley de Bragg y red recíproca

Aunque en el tema anterior se hizo gran énfasis en la relación entre las familias de planos y la red recíproca, es posible escribir la ley de Bragg en una forma que hace esta relación es más explícita.

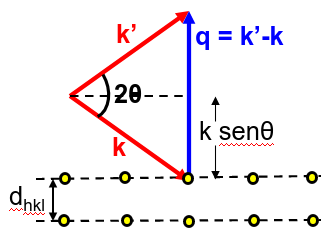
Fig. 95 Diagrama donde puede apreciarse que la diferencia del vector entrante \(\vec{k}\) y saliente \(\vec{k}^\prime\) es perpendicular a los planos de red y, por tanto, es paralelo a \(\vec{g}_{hkl}\).

Utilizando como referencia Fig. 95 primero notamos que la diferencia de vectores de onda entrante y saliente \(\vec{k}-\vec{k}^\prime\) es un vector normal a los planos interatómicos que es la que tenía el vector \(\vec{g}_{hkl}\) que caracterizaba los índices de Miller, que era un vector de la red recíproca convencional. Seguidamente probaremos que no sólo coincide en dirección si no que también lo hace en módulo, llegando a una importante expresión que es la forma vectorial de la ley de Bragg.

Para probar esta afirmación se observa que la difracción de rayos-X es un proceso elástico,

(101)\[\vert\vec{k}^\prime \vert= \vert\vec{k} \vert=\frac{2\pi}{\lambda}\]

y que, geométricamente, (Fig. 95) se cumple,

(102)\[\vert\vec{k}^\prime -\vec{k}\vert= 2k\sin\theta = 2\frac{2\pi}{\lambda}\sin\theta\]

A partir de la ley de Bragg y usando la relación de la distancia interplanar con el vector \(\vec{g}_{hkl}\), Ec. (92), obtenemos,

(103)\[2d_{hkl}\sin\theta = \lambda \rightarrow \lambda = 4\pi\frac{\sin\theta}{g_{hkl}}\]

Combinando las Ecs. (102) y (103) llegamos precisamente a que,

(104)\[\vec{k}^\prime-\vec{k}=\vec{g}_{hkl}\]

Es decir, que la diferencia de vectores de onda es, precisamente, un vector de la red recíproca. Este tipo de expresiones, muy comunes en física del estado sólido tienen directamente que ver con la simetría traslacional de los cristales y son una forma de conservación del momento cristalino[3].

Basada en la Ec. (104) se define el plano de Bragg como el plano que bisecta un vector de la red recíproca (ver Fig. 96). Este es el plano de todos los vectores de onda que producen difracción y que son claves para entender las ondas en los sólidos.

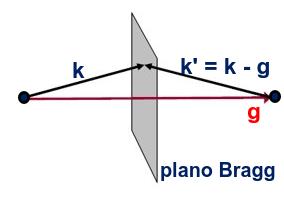
Fig. 96 El plano de Bragg (mostrado en gris) es el plano que bisecta a un vector de la red recíproca \(\vec{g}\). Todas las parejas de vectores \(\vec{k}\) y \(\vec{k}^\prime\) que se tocan en el plano producen difracción.

Problemas y ejemplos