Implicaciones de la simetría

Implicaciones de la simetría#

(175)#\[\left[\hat{H},\hat{O}\right]=0\]

Hamiltoniano molecula y cristalino#

../_images/Bencene-regular1.png — Fig. 115 Benceno sin hidrógeno#

(176)#\[\hat{H}(\vec{r},\vec{R})=\hat{T}(\vec{r})+\hat{V}_{ee}(\vec{r})+\hat{V}_{en}(\vec{r},\vec{R})+V_{nn}(\vec{R})\]

(177)#\[\hat{O}\hat{H}_{el}(\vec{R})=\hat{H}_{el}(\vec{R}^\prime)=\hat{H}_{el}(\vec{R})\]

Grupo de las operaciones de simetría#

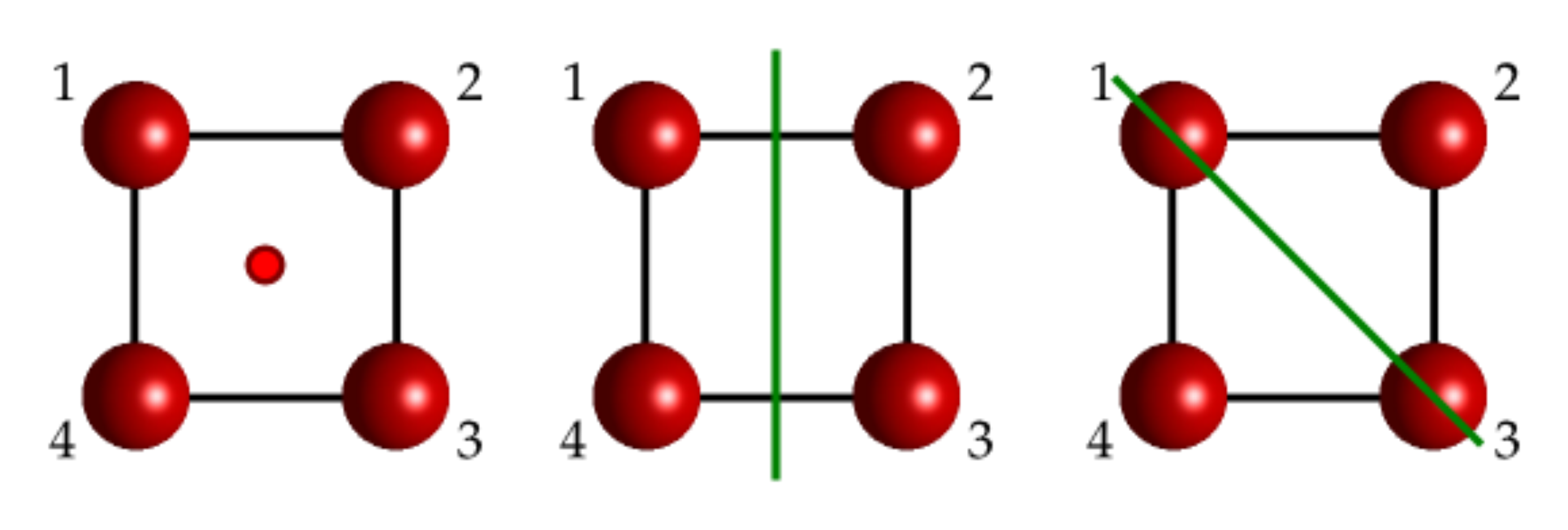
../_images/symm_group.png — Fig. 116 Operaciones de simetría del grupo D\(_{4h}\)#

Operaciones conjugadas y clases#

(178)#\[R_3 R_2 R_3^{-1} = R_1\]

Ejemplo: Amoníaco

Clases

../_images/ops_conjugadas.png — Fig. 117 Operaciones de simetría conjugadas del grupo D\(_{3h}\)#

Leyes de conservación#

(179)#\[ \frac{d\left\langle\hat{O}\right\rangle}{dt} = \frac{1}{i\hbar} \left\langle \left[\hat{H}_{el},\hat{O}\right] \right \rangle\]

(180)#\[ \frac{d\left\langle\hat{O}\right\rangle}{dt} = 0\]

(181)#\[ \theta \longrightarrow \theta + \Delta \theta \frac{\partial}{\partial \theta} +...\]

(182)#\[ \frac{\partial }{\partial \theta} H_{el} = 0 \longrightarrow [H_{el},\frac{\partial }{\partial \theta}]=0\]

(183)#\[[H_{el},\frac{\partial }{\partial \theta}]\Psi = H_{el}\frac{\partial }{\partial\theta}\Psi - \frac{\partial }{\partial\theta} (H_{el}\Psi) = H_{el}\frac{\partial }{\partial\theta}\Psi - \frac{\partial H_{el}}{\partial\theta} \Psi - H_{el} \frac{\partial \Psi}{\partial\theta} = 0\]

Conservación del momento angular#

(184)#\[l_{z}=-i\hbar\frac{\partial}{\partial \theta}\]

../_images/rotaciones_symm.png — Fig. 118 Operaciones de simetría del grupo D\(_{4h}\)#