Transformada de Laplace

La transformada de Laplace recibe su nombre en honor del matemático francés Pierre-Simon Laplace (1749-1827). Es una transformada integral que convierte una función \(f(t)\) de una variable real \(t\) (normalmente el tiempo) a una función \({\cal L}[f](s)\) de variable compleja \(s\). Se trata de una herramienta matemática con gran variedad de aplicaciones, entre ellas permite transformar ecuaciones diferenciales en ecuaciones algebraicas.

Transformada de Laplace:

Dada una función \(f(t)\) con \(0\leq t\leq\infty\), su transformada de Laplace se define como

\[F(s)={\cal L}[f](s)=\int_{0}^{\infty} f(t)e^{-st}dt\]

siempre que la integral converja.

La transformada de Laplace es una integral impropia

\[\int_{0}^{\infty} f(t)e^{-st}dt=\lim_{k\rightarrow\infty}\int_{0}^{k} f(t)e^{-st}dt\]

Las integrales impropias que definen las transformadas de Laplace puede ser calculadas con la rutina de integración simbólica del paquete SymPy, además, ese paquete cuenta con una función propia que calcula dichas transformadas. Para su utilización en el resto del Notebook se importa el paquete

import sympy as sp

---

Ejemplo:

Transformada de Laplace de la función \(f(t)=1\)

\[F(s)={\cal L}[1](s)=\int_{0}^{\infty} e^{-st}dt= \left.\frac{-1}{s}e^{-st}\right|_0^\infty = \frac{1}{s}\]

A continuación puede verse como calcular dicha transformada con las funcionalidades del paquete SymPy. En primer lugar conviene aclarar cómo se denota el infinito:

• En el caso del paquete SymPy: sp.oo

• En el caso del paquete NumPy: np.inf

t,s = sp.symbols('t,s')
sp.integrate(sp.exp(-s*t), (t, 0, sp.oo))

\[\begin{split}\displaystyle \begin{cases} \frac{1}{s} & \text{for}\: \left|{\arg{\left(s \right)}}\right| < \frac{\pi}{2} \\\int\limits_{0}^{\infty} e^{- s t}\, dt & \text{otherwise} \end{cases}\end{split}\]

La forma más rápida de calcular simbólicamente transformadas de Laplace es mediante la función laplace_transform(). Esta función devuelve la función transformada y condiciones de convergencia. Al ser una integral impropia, es importante tener en cuenta posibles condiciones de convergencia. La convergencia normalmente exige que la variable compleja \(s\) cumpla una condición \(Re(s)>a\). La función laplace_transform() devuelve tres cosas:

• Función transformada

• Valor \(a\) de la condición de convergencia \(Re(s)>a\)

• Posibles condiciones auxiliares de convergencia

f = 1
sp.laplace_transform(f, t, s)

(1/s, 0, True)

Como puede verse, la transformada de Laplace de \(f(t)=1\) es \(1/s\), para los puntos tales que \(Re(s)>0\).

Si lo único que se desea obtener es la transformada, se puede usar el parámetro opcional noconds

sp.laplace_transform(f, t, s, noconds=True)

\[\displaystyle \frac{1}{s}\]

---

Ejemplo:

Transformada de Laplace de la función \(f(t)=t^n\)

\[ F(s)={\cal L}[t^n](s)=\int_{0}^{\infty} t^ne^{-st}dt= \left.t^n\frac{e^{-st}}{-s}\right|_0^\infty -\int_{0}^{\infty} nt^{n-1}\frac{e^{-st}}{-s}dt\]

\[ = \frac{n}{s}\int_{0}^{\infty} t^{n-1}e^{-st}dt=\frac{n}{s}{\cal L}[t^{n-1}](s)\]

Como \({\cal L}[t^0](s)=1/s\), por recurrencia se obtiene

\[{\cal L}[t^n](s)=\frac{n!}{s^{n+1}}\]

t,s = sp.symbols('t,s')
[sp.laplace_transform(t**n, t, s, noconds=True) for n in range(1,6)]

[s**(-2), 2/s**3, 6/s**4, 24/s**5, 120/s**6]

---

Ejemplo:

Transformada de Laplace de la función \(f(t)=e^{at}\)

\[F(s)={\cal L}[e^{at}](s)=\int_{0}^{\infty} e^{at}e^{-st}dt=\int_{0}^{\infty} e^{-(s-a)t}dt\]

\[=\left. \frac{-1}{s-a}e^{-(s-a)t}\right|_0^\infty = \frac{1}{s-a}\;\;\;\mbox{si }s>a\]

t,s = sp.symbols('t,s')
a = sp.symbols('a', real=True, positive=True)
f = sp.exp(a*t)
sp.laplace_transform(f, t, s)

(1/(-a + s), a, True)

---

Ejemplo:

Transformada de Laplace de funciones trigonométricas

\[F(s)={\cal L}[\sin(at)](s)=\int_{0}^{\infty} \sin(at)e^{-st}dt=\frac{a}{s^2+a^2}\]

\[F(s)={\cal L}[\cos(at)](s)=\int_{0}^{\infty} \cos(at)e^{-st}dt=\frac{s}{s^2+a^2}\]

t,s,a = sp.symbols('t,s,a')
f = sp.sin(a*t)
sp.laplace_transform(f, t, s, noconds=True)

\[\displaystyle \frac{a}{a^{2} + s^{2}}\]

t,s,a = sp.symbols('t,s,a')
f = sp.cos(a*t)
sp.laplace_transform(f, t, s, noconds=True)

\[\displaystyle \frac{s}{a^{2} + s^{2}}\]

Transformada de Laplace de la función de Heaviside y de la delta de Dirac

Por sus aplicaciones prácticas en campos relacionados con la electrónica y el análisis de señales, puede ser de interés analizar las transformadas de Laplace de dos funciones especiales:

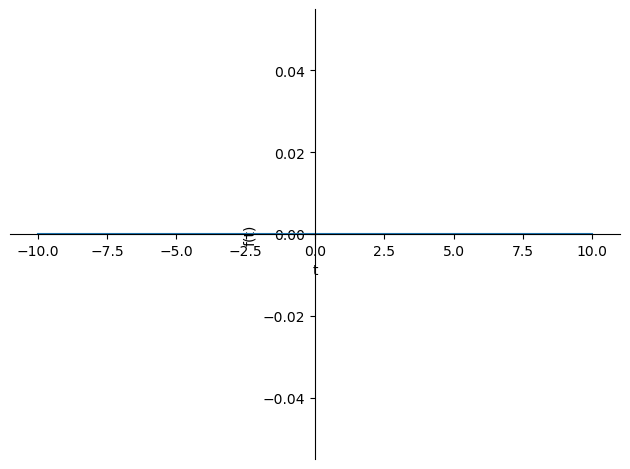
• Impulso unitario (delta de Dirac): realmente la delta de Dirac no es una función, porque exigiría tomar un valor infinito en el origen. La delta de Dirac \(\delta(x)\) sería una función que tiende a infinito cuando \(x=0\) y para cualquier otro valor \(\delta(x)=0\) si \(x\neq 0\),

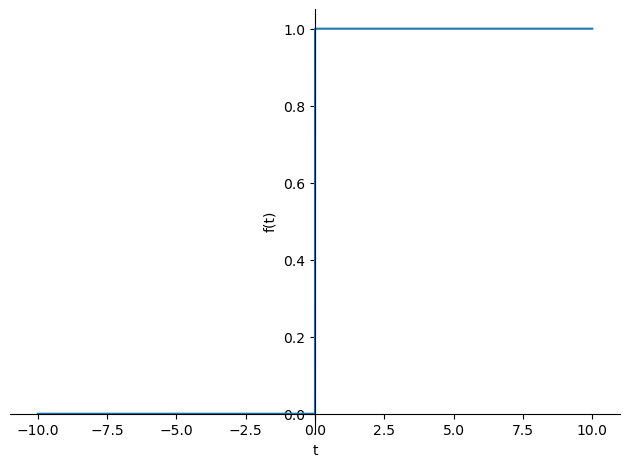
• Escalón unitario (función de Heaviside): cuyo valor es 0 para cualquier argumento negativo, y 1 para cualquier argumento positivo, incluido el cero. Es decir:

\[\begin{split}H(x)=\left\{\begin{array}{}0 & si\;x<0 \\ 1 & si\;x\geq 0 \end{array}\right.\end{split}\]

Ambas funciones se encuentran definidas en el paquete SymPy y pueden fácilmente representarse gráficamente:

t = sp.Symbol('t')
sp.DiracDelta(t)

\[\displaystyle \delta\left(t\right)\]

sp.plot(sp.DiracDelta(t));

sp.plot(sp.Heaviside(t));

Suele ser habitual realizar un desplazamiento sobre dichas funciones, por ejemplo para que el impulso unitario de la delta de Dirac se sitúe en \(x=2\), se podría considerar la expresión

sp.DiracDelta(t-2)

\[\displaystyle \delta\left(t - 2\right)\]

sp.DiracDelta(t-2).subs(t,0)

\[\displaystyle 0\]

sp.DiracDelta(t-2).subs(t,2)

\[\displaystyle \delta\left(0\right)\]

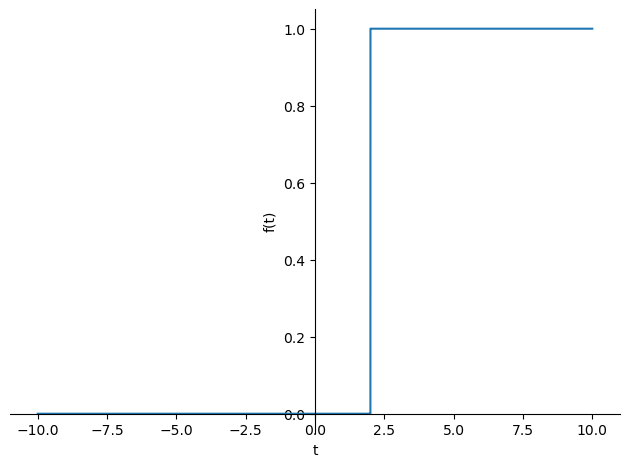
De la misma manera puede realizarse un desplazamiento sobre la función de Heaviside para construir la función \(H_a(x)\) que tome el valor 1 para argumentos mayores o iguales que \(a\)

a=2
sp.plot(sp.Heaviside(t-a));

Tanto la delta de Dirac como la función de Heaviside admiten sus respectivas transformadas de Laplace:

a = sp.symbols('a', real=True, positive=True)
delta = sp.DiracDelta(t-a)
sp.laplace_transform(delta,t,s)

(exp(-a*s), 0, True)

h = sp.Heaviside(t)
sp.laplace_transform(h,t,s)

(1/s, 0, True)

a = sp.symbols('a', real=True, positive=True)
h = sp.Heaviside(t-a)
sp.laplace_transform(h,t,s)

(exp(-a*s)/s, 0, True)

Tabla de transformadas de las funciones básicas

A modo de resumen, la siguiente tabla muestra las integrales de Laplace de algunas funciones habituales que surgen en aplicaciones prácticas.

Función inicial \(f(t)\)	Transformada de Laplace \(L[f](s)\)
\(1\)	\(\frac{1}{s}\)
\(t^n\)	\(\frac{n!}{s^{n+1}}\)
\(e^{at}\)	\(\frac{1}{s-a}\)
\(\sin(at)\)	\(\frac{a}{s^2+a^2}\)
\(\cos(at)\)	\(\frac{s}{s^2+a^2}\)
\(H_a(t)\)	\(\frac{e^{-as}}{s}\)
\(e^{at}\sin(bt)\)	\(\frac{b}{(s-a)^2+b^2}\)
\(e^{at}\cos(bt)\)	\(\frac{s-a}{(s-a)^2+b^2}\)
\(t^ne^{at}\)	\(\frac{n!}{(s-a)^{n+1}}\)

Propiedades de la transformada de Laplace

La transformada de Laplace cumple una serie de propiedades que deben tenerse en cuenta a la hora de calcular determinadas transformadas, así como para entender algunas de sus aplicaciones.

Linealidad de la transformada de Laplace

Si \({\cal L}[f](s)\) y \({\cal L}[g](s)\) están definidas en un intervalo \(s>s_0\), entonces también lo está \({\cal L}[\alpha f+\beta g](s)\) para cualesquiera \(\alpha,\beta\in R\), además:

\[{\cal L}[\alpha f+\beta g](s) = \alpha{\cal L}[f](s) + \beta{\cal L}[g](s)\]

Por ejemplo,

\[{\cal L}[5+2e^{3t}-6\sin(5t)](s) = 5{\cal L}[1](s)+2{\cal L}[e^{3t}](s)-6{\cal L}[\sin(5t)](s)\]

\[=5\frac{1}{s}+2\frac{1}{s-3}-6\frac{5}{s^2+25}\]

t,s = sp.symbols('t,s')
f = 5 + 2*sp.exp(3*t) - 6*sp.sin(5*t)
sp.laplace_transform(f, t, s, noconds=True)

\[\displaystyle - \frac{30}{s^{2} + 25} + \frac{2}{s - 3} + \frac{5}{s}\]

Derivada de la transformada de Laplace

\[F(s)={\cal L}[f(t)](s)=\int_{0}^{\infty} f(t)e^{-st}dt\]

\[\frac{d}{ds}F(s)=\int_{0}^{\infty}\frac{d}{ds} f(t)e^{-st}dt= -\int_{0}^{\infty} t\,f(t)e^{-st}dt\]

\[F'(s)={\cal L}[-t\,f(t)](s)\]

Transformada de Laplace de las derivadas de una función

\[{\cal L}[f'(t)](s)=s{\cal L}[f(t)](s)-f(0)\]

\[{\cal L}[f''(t)](s)=s^2{\cal L}[f(t)](s)-s\,f(0)-f'(0)\]

\[\vdots\]

\[{\cal L}[f^{(n)}(t)](s)=s^n{\cal L}[f(t)](s)-s^{n-1}\,f(0)-s^{n-2}f'(0)-\dots-f^{(n-1)}(0)\]

Transformadas inversas

La operación de calcular transformadas de Laplace es invertible, es decir, dada una función \(L(s)\) podría tener interés calcular una función \(f(t)\) cuya transformada sea la primera. Esa operación puede realizarse directamente con la función inverse_laplace_transform() implementada en SymPy.

Hs = s/(s**2+3*s+2)
Ht = sp.inverse_laplace_transform(Hs,s,t)
print(Ht)

(2 - exp(t))*exp(-2*t)*Heaviside(t)

Ht

\[\displaystyle \left(2 - e^{t}\right) e^{- 2 t} \theta\left(t\right)\]

us  = 1/s
u = sp.inverse_laplace_transform(us,s,t)
u

\[\displaystyle \theta\left(t\right)\]

Aplicación a la resolución de ecuaciones diferenciales

Una de las aplicaciones de la transformada inversa es la resolución de problemas de valor inicial en ecuaciones diferenciales. La idea sería proceder de la siguiente manera:

• Se aplica la transformada de Laplace a la ecuación completa

• De la ecuación algebraica resultante se obtiene la transformada de la función incógnita

• Se aplica la transformación inversa para obtener la solución de la ecuación.

En el siguiente ejemplo se ilustra este proceso

\[\begin{split} \left\{ \begin{array}{l} y''(t)-y(t)= 1\\ y(0)=0,\;\;\,y'(0)=1 \\ \end{array} \right. \end{split}\]

Aplicando la transformada de Laplace:

\[{\cal L}[y''-y]={\cal L}[1]\]

Teniendo en cuenta la propiedad de linealidad:

\[{\cal L}[y'']-{\cal L}[y]={\cal L}[1]\]

y teniendo en cuenta las expresiones que relacionan la transformada de las funciones derivadas con la transformada de la función:

\[s^2{\cal L}[y]-s\,y(0)-y'(0)-{\cal L}[y]=\frac{1}{s}\Rightarrow {\cal L}[y]=\frac{1+\frac{1}{s}}{s^2-1}\]

Utilizando el método de descomposición en fracciones simples se obtendría:

\[{\cal L}[y]=\frac{1}{s-1}-\frac{1}{s},\;\;\;s>1\]

Finalmente invirtiendo el proceso, es decir, aplicando la transformada inversa, se obtiene:

\[y=e^t-1\]

que sería la solución de la ecuación diferencial

A continuación se muestra cómo calcular la última transformada inversa con SymPy y la comprobación de que efectivamente se obtiene la solución de la ecuación con las condiciones iniciales dadas.

t,s = sp.symbols('t,s')
L = (1+1/s)/(s**2-1)
sp.inverse_laplace_transform(L,s,t)

\[\displaystyle \left(e^{t} - 1\right) \theta\left(t\right)\]

La solución \(y(t)=e^t-1\) sería válida para los valores \(t\geq 0\)

t = sp.Symbol('t')
y = sp.Function('y')
edo = sp.Eq(y(t).diff(t,2) - y(t), 1)
condiciones = {y(0):0, y(t).diff(t).subs(t,0):1}
sp.dsolve(edo, ics=condiciones)

\[\displaystyle y{\left(t \right)} = e^{t} - 1\]

Ejercicios propuestos

• Calcular la transformada de Laplace de las funciones:

\[\begin{split}f(t)=\left\{ \begin{array}{ll} 1 & \mbox{si }0\leq t\leq 1\\ 0 & \mbox{si }t>1\\ \end{array}\right.\end{split}\]

\[g(t)=e^{3t}-t^3+2t^2-3t+5\]

• Utilizar la transformada de Laplace para resolver los problemas

\[\begin{split}\left\{ \begin{array}{l} y'(t)+2y(t)= 4t^3e^{-2t}\\ y(0)=1 \\ \end{array}\right. \end{split}\]

\[\begin{split}\left\{ \begin{array}{l} y''(t)+4y'(t)+4y(t)= 0\\ y(0)=0,\;\;\;y'(0)=5 \\ \end{array}\right.\end{split}\]

\[\begin{split}\left\{ \begin{array}{l} y''(t)+9y(t)= \sin(3t)\\ y(0)=2,\;\;\;y'(0)=1 \\ \end{array}\right.\end{split}\]