Teoremas de la divergencia y de Stokes#
Los teoremas de la divergencia y el de Stokes constituyen, junto con el teorema de Green, los resultados más importantes del cálculo vectorial integral. Son resultados muy utilizados en la física y en diferentes ramas de la ingeniería, que relacionan los distintos tipos de integrales analizadas: integrales curvilíneas, integrales de superficie e integrales múltiples.
Teorema de la divergencia#
El teorema de la divergencia, también conocido como teorema de Gauss, puede verse como la versión tridimensional del teorema de Green que relacionaba las integrales curvilíneas sobre curvas cerradas con la integración doble.
Dado un recinto \(D\subset R^3\) con superficie frontera \(S\), el teorema de la divergencia relaciona, bajo ciertas condiciones, el flujo de un campo vectorial sobre la superficie con la integral triple de la divergencia del campo sobre el recinto tridimensional.
Teorema de la divergencia o teorema de Gauss:
Si \(S\) es una superficie cerrada que delimita una región \(D\subset R^3\) y orientada según la normal saliente, y \(\vec{F}\) es un campo vectorial definido y diferenciable en todos los puntos de \(D\), entonces se verifica
Este teorema facilita la resolución de determinadas integrales de superficie.
Ejemplo:
Se desea calcular el flujo del campo vectorial \(\vec{F}=z\vec{k}\) sobre la superficie de la esfera de radio \(R\) y centrada en el origen. Si se tiene en cuenta que la divergencia del campo es:
el flujo se calcularía de una manera muy simple:
Como consecuencia del teorema de la divergencia, se podría decir que aquellos campos vectoriales que cumplen \(div\,\vec{F}=0\) tendrían flujo nulo sobre cualquier superficie cerrada en la que se encuentren definidos y sean diferenciables. Los campos cuya divergencia es nula reciben el nombre de campos solenoidales.
En particular, el rotacional de un campo vectorial es un campo solenoidal, ya que
Ejemplo:
En el siguiente ejemplo se comprueba como efectivamente se cumple lo establecido en el teorema de Gauss.
Como superficie cerrada se considera de nuevo la esfera \(x^2+y^2+z^2=1\) y el campo \(\vec{F}=(x+y)\vec{i}+(z^2-y)\vec{k}\). Debe recordarse que dentro del módulo Vector se cuenta con la función divergence() que permite calcular la divergencia de un campo.
Para comenzar se definen de manera paramétrica tanto la superficie de la esfera como la esfera como sólido. Previamente es necesario importar los paquetes de cálculo simbólico y definir un sistema de coordenadas:
import sympy as sp
import sympy.vector as vec
S = vec.CoordSys3D('')
phi, theta, r = sp.symbols("phi theta r")
superficie = vec.ParametricRegion((sp.sin(phi)*sp.cos(theta), sp.sin(phi)*sp.sin(theta), sp.cos(phi)),
(phi, 0, sp.pi), (theta, 0, 2*sp.pi))
solido = vec.ParametricRegion((r*sp.sin(phi)*sp.cos(theta), r*sp.sin(phi)*sp.sin(theta), r*sp.cos(phi)),
(r, 0, 1), (phi, 0, sp.pi), (theta, 0, 2*sp.pi))
La integral de superficie del campo sobre la superficie de la esfera sería:
F = (S.x+S.y)*S.i + (S.z**2-S.y)*S.k
vec.vector_integrate(F, superficie)
vec.vector_integrate(F, superficie).simplify()
vec.vector_integrate(F, superficie).evalf()
La divergencia del campo F sería:
vec.divergence(F)
y la integral triple de la esfera sólida puede también ser calculada con la propia función vector_integrate() que al detectar que la región paramétrica tiene 3 parámetros automáticamente calcula una integral triple.
vec.vector_integrate(vec.divergence(F), solido)
Teorema de Stokes#
El teorema de Stokes relaciona la circulación de un campo sobre una curva \(C\) con el flujo del rotacional de dicho campo sobre una superficie que se apoye en la curva, es decir, sobre una superficie \(S\) cuyo “borde” sea la curva \(C\). En cierta forma es una generalización del teorema de Green para el caso tridimensional.
Teorema de Stokes:
Dado un campo vectorial \(\vec{F}\) y una curva cerrada \(C\) en el espacio, para cualquier superficie \(S\) que se apoye en \(C\) y para la cuál el campo \(\vec{F}\) esté definido y sea diferenciable en todos sus puntos, se verifica:
siempre que la superficie sea orientable y tenga una orientación compatible con la orientación de la curva.
Conviene aclarar dos aspectos:
El significado del concepto de superficie apoyada en una curva.
La compatibilidad de la orientación de la curva y la superficie.
Para entender mejor estos requisitos la siguiente figura muestra varios ejemplos de superficies apoyadas en una misma curva cerrada.
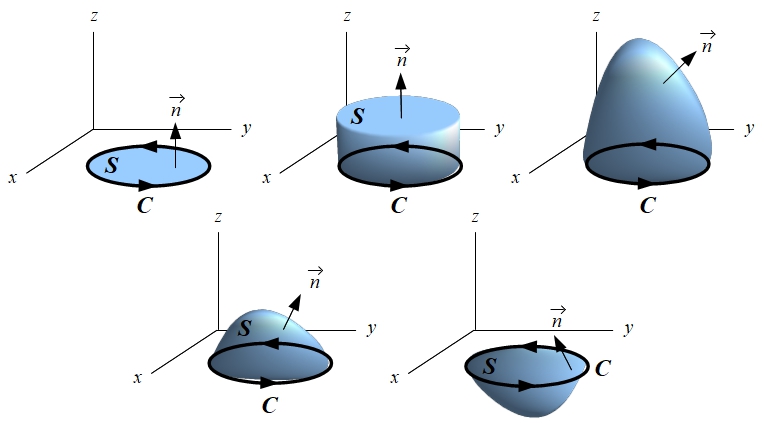
Si la curva cerrada tiene una orientación positiva dejando la superficie a la izquierda, entonces la superficie debe estar orientada con la normal hacia arriba. Para comprobar la compatibilidad de las orientaciones podría utilizarse la “regla del sacacorchos”.
El teorema de Stokes establece que, sea cual sea la superficie apoyada en la curva, la integral de línea del campo sobre la curva cerrada es igual al flujo del rotacional sobre la superficie. En el caso concreto de una curva cerrada completamente contenida en el plano \(OXY\), si se considera como superficie la propia región del plano comprendida dentro de la curva, el teorema de Stokes establecería lo mismo que el teorema de Green.
Si se considera un campo \(\vec{F}=P\vec{i}+Q\vec{j}+R\vec{k}\), al estar la curva completamente contenida en el plano \(OXY\), se cumple \(z=0\) y por tanto \(dz=0\). Entonces
De acuerdo al teorema de Stokes, esta última integral es igual a
El vector normal a la superficie es \(\vec{n}=(0,0,1)\), y por tanto el producto escalar del vector normal por el rotacional será la tercera componente del propio rotacional: \(rot\vec{F}\cdot\vec{n}=\frac{\partial Q}{\partial x}-\frac{\partial P}{\partial y}\). Teniendo en cuenta esto, el teorema de Stoke en este caso establece la igualdad:
que es la propiedad establecida en el teorema de Green.
Ejemplo:
Dado el campo vectorial \(\vec{F}=z\vec{i}+x\vec{j}+y\vec{k}\), si se desea calcular el trabajo ejercido por el campo sobre una partícula que se desplaza en sentido positivo por la circunferencia de radio 1 en el plano \(OXY\) y centrada en el origen, habría dos alternativas:
Directamente, calculando la integral de línea. Para ello se consideraría la parametrización \(\vec{r}(t)=(\cos t,\sin t,0)\) con \(t\in[0,2\pi]\).
Utilizando una superficie \(S\) apoyada sobre la curva y el teorema de Stokes. Por ejemplo, puede considerarse como superficie \(S\) el paraboloide \(z=1-x^2-y^2\). En este caso, al estar la superficie definida por una ecuación explícita de la forma \(z=f(x,y)\), se cumple
Por otro lado, el rotacional del campo es
Aplicando la equivalencia establecida por el teorema de Stokes, se obtendría el trabajo mediante la siguiente integral doble:
Esta última integral puede calcularse mediante coordenadas polares, obteniendo finalmente
Como puede comprobarse, con ambas alternativas se obtendría el mismo resultado.
En Python también es sencillo el cálculo de las dos integrales, la de superficie y la de línea.
campo = S.z*S.i + S.x*S.j + S.y*S.k
t = sp.symbols('t')
circunferencia = vec.ParametricRegion((sp.cos(t), sp.sin(t), 0), (t, 0, 2*sp.pi))
# integral de línea:
vec.vector_integrate(campo, circunferencia)
rotCampo = vec.curl(campo)
rotCampo
u,v = sp.symbols('u,v')
paraboloide = vec.ParametricRegion((u*sp.cos(v), u*sp.sin(v), 1-u**2), (u, 0, 1), (v, 0, 2*sp.pi))
# integral de superficie:
vec.vector_integrate(rotCampo, paraboloide)
Ejemplo:
De nuevo, el siguiente ejemplo comprueba la igualdad de las dos integrales que establece en teorema de Stokes. En este caso se considera una circunferencia sobre la que se apoya un cono y sobre los que actúa el campo \(\vec{F}=(x+y+z)\vec{i}+(x^2-yz)\vec{j}+(x-z^2)\vec{k}\)
La circunferencia será la que tiene por ecuación \(x^2+y^2=1\) situada sobre el plano \(z=1\), y la superficie que se apoya sobre ella es la parte del cono \(x^2+y^2=z^2\) con la condición \(z\geq 0\). En la siguiente imagen se ve la disposición de la curva y la superficie.
import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
# circunferencia unidad en el plano z=1
t = np.linspace(0, 2*np.pi)
x, y, z = np.cos(t), np.sin(t), 1
ax.plot(x,y,z, color='b', linewidth=4)
# representación del cono
u, v = np.meshgrid(np.linspace(0, 2*np.pi), np.linspace(0, 1))
sx, sy, sz = v*np.cos(u), v*np.sin(u), v
ax.plot_surface(sx, sy, sz, cmap='viridis', alpha=0.5)
plt.show()
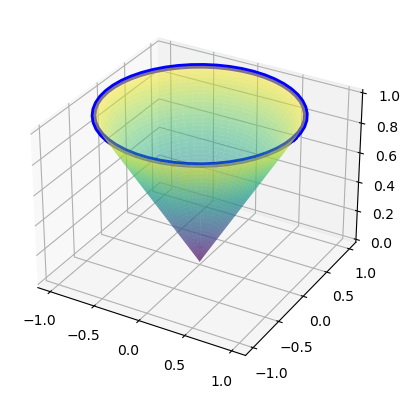
La definición paramétrica de la curva (circunferencia) y superficie (cono) en forma simbólica es la siguiente:
theta, r = sp.symbols("theta,r")
circunferencia = vec.ParametricRegion((sp.cos(theta), sp.sin(theta), 1), (theta, 0, 2*sp.pi))
cono = vec.ParametricRegion((r*sp.cos(theta), r*sp.sin(theta), r), (r, 0, 1), (theta, 0, 2*sp.pi))
El campo vectorial sobre el sistema de coordenadas S es el que se define a continuación:
F=(S.x+S.y+S.z)*S.i + (S.x**2-S.y*S.z)*S.j + (S.x-S.z**2)*S.k
La integral de linea del campo sobre la circunferencia sería:
vec.vector_integrate(F, circunferencia)
La integral de superfice del rotacional (curl) sobre el cono es:
vec.vector_integrate(vec.curl(F), cono)
Ambas integrales son iguales, tal como establece el teorema de Stokes. Además, al tener signo negativo el balance del flujo es contrario al sentido del vector normal de la superficie. El teorema de Stokes establece que la curva en la que se apoya la superficie se recorre en sentido positivo y el sentido del vector normal a la suerficie se determina con la “regla del sacacorchos”. En este caso, la regla establecería que la normal sería hacia el interior del cono.
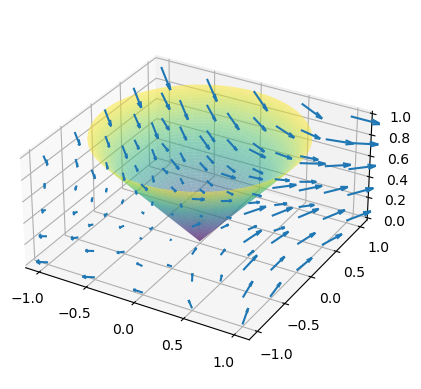
Al ser el flujo negativo, iría en dirección contraria y por tanto sería un flujo de salida (del interior al exterior del cono). En la siguiente figura se representa de nuevo el cono, pero esta vez junto al campo.
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
# representación del cono
u, v = np.meshgrid(np.linspace(0, 2*np.pi), np.linspace(0, 1))
sx, sy, sz = v*np.cos(u), v*np.sin(u), v
ax.plot_surface(sx, sy, sz, cmap='viridis', alpha=0.5)
# representación del campo
xx, yy, zz = np.meshgrid(np.linspace(-1,1,5), np.linspace(-1,1,5), np.linspace(0,1,5))
ax.quiver(xx, yy, zz, xx+yy+zz, xx**2-yy*zz, xx-zz**2, length=0.1)
ax.set_box_aspect([1, 1, 0.5])
plt.show()
Ejercicios propuestos#
Comprobar que se cumple el teorema de la divergencia para el campo vectorial \(\vec{F}=3xy\vec{i}+y^2\vec{j}-(x+4y)\vec{k}\) y la superficie del tetraedro acotado por los planos coordenados y el plano de ecuación \(x+y+2z=1\).
Calcular el flujo del campo \(\vec{F}=x^3\vec{i}+y^3\vec{j}+z^3\vec{k}\) a través de la superficie del cono \(x^2+y^2=z^2\), con \(0\leq z\leq 1\) de dos maneras diferentes: directamente y aplicando el teorema de la divergencia
Utilizar el teorema de la divergencia para calcular \(\iint_S \vec{F}\cdot d\vec{s}\) siendo \(\vec{F}=xy\vec{i}+(y^2+e^{xz^2})\vec{j}+\sin(xy)\vec{k}\) siendo \(S\) la superficie de la región delimitada por el cilindro parabólico \(z=1-x^2\) y los planos \(z=0\), \(y=0\), \(y+z=2\)
Comprobar que se verifica el teorema de Stokes para el campo vectorial \(\vec{F}=3y\vec{i}+4z\vec{j}-6x\vec{k}\) y la superficie paraboloide \(z=9-x^2-y^2\) apoyada sobre la circunferencia de centro \((0,0)\) y radio 3 en el plano \(OXY\) y con orientación normal hacia arriba.
Calcular, utilizando el teorema de Stokes, la siguiente integral \(\oint_C (-y^3dx+x^3dy-z^3dz)\) donde \(C\) es la intersección del cilindro \(x^2+y^2=1\) con el plano \(x+y+z=1\), recorrida en sentido positivo.