Transformada de Fourier

En general, una transformada integral es una transformación \(T\) que convierte una función \(f(t)\) en otra función \(F(u)\) definida en otro dominio. La transformación tiene la forma general

\[T(f(t))=\int_{t_1}^{t_2}K(u,t)f(t)dt=F(u)\]

La función \(K(u,t)\) se conoce como núcleo de la transformación y determina el tipo de transformada.

El uso de transformadas integrales puede ayudar a resolver diferentes problemas de naturaleza matemática que son difíciles de resolver en su dominio original. Mediante la transformada el problema se lleva a otro dominio en el que puede resultar más fácil de resolver.

Transformadas integrales hay muchas, en este caso el análisis se va a centrar en dos de las que tienen mayores aplicaciones prácticas en la física y distintas ramas de la ingeniería:

• Transformada de Fourier

• Transformada de Laplace

Definición de la transformada de Fourier

La transformada de Fourier, propuesta por el matemático y físico francés Joseph Fourier (1768-1830), transforma señales entre el dominio del tiempo (o el espacio) y el dominio de la frecuencia. Se trata de una transformación que tiene muchas aplicaciones en la física y la ingeniería. Es reversible, siendo capaz de transformarse en cualquiera de los dominios al otro.

Transformada de Fourier:

Dada \(f(t)\) localmente integrable y absolutamente integrable en \(R\), se define su transformada de Fourier como:

\[F(w)=F(f(t))(w)=\int_{-\infty}^{\infty} f(t)e^{-iwt}dt\]

y se llama transformada inversa o anti-transformada de Fourier de la función \(F(w)\) a la función:

\[f(t)=F^{-1}[F(w)]=\frac{1}{2\pi}\int_{-\infty}^{\infty} F(w)e^{iwt}dw\]

Estas expresiones permiten calcular el dominio de la frecuencia \(F(w)\) a partir del dominio del tiempo \(f(t)\), y viceversa.

Cálculo de transformadas de Fourier con Python

El cálculo de esta transformada puede también hacerse con ayuda del paquete SymPy de Python. Este paquete cuenta con una función que permite calcular la transformada de Fourier directamente. Se trata de la función fourier_transform(), lo único que se debe advertir es que está función calcula la transformada de la siguiente manera:

\[F(k) = \int_{-\infty}^\infty f(x) e^{-2\pi i x k} dx\]

Para lo que recibe los siguientes argumentos:

• Función a transformar \(f(x)\)

• Variable respecto a la que se calcula la transformada \(x\)

• Variable de la frecuencia \(k\)

Teniendo en cuenta la pequeña diferencia en la definición, para calcular \(F(f(t))(w)\) habría que utilizar como tercer argumento de la función \(\frac{w}{2\pi}\). En definitiva, para calcular la transformada de Fourier de \(f(t)\) habría que utilizar la instrucción

fourier_transform(f, t, w/(2*sp.pi))

Para hacer uso de esa función habría que cargar previamente el paquete

import sympy as sp

A continuación se muestran las transformadas de Fourier de algunas funciones habituales en modelos físicos.

---

Ejemplo: transformada de Fourier de la función pulso rectangular

\[\begin{split}f(t)=\left\{ \begin{array}{ll} 1 & \mbox{si }|t|\leq 1 \\ 0 & \mbox{si }|t|> 1 \\ \end{array} \right.\end{split}\]

Esta función puede definirse a partir de la función de Heaviside que se encuentra ya definida dentro del paquete SymPy:

\[\begin{split}H(t)=\left\{ \begin{array}{ll} 1 & \mbox{si }t\geq 0 \\ 0 & \mbox{si }t<0\\ \end{array} \right.\end{split}\]

En concreto

\[f(t)=H(t+1)H(1-t)\]

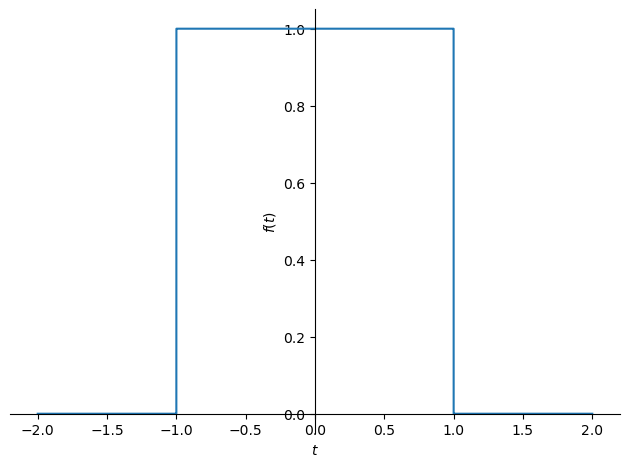
Con ayuda de SymPy puede definirse y representarse gráficamente la función pulso rectangular:

t = sp.Symbol('t')
f = sp.Heaviside(t+1) * sp.Heaviside(1-t)
sp.plot(f,(t,-2,2));

Otra opción para representar gráficamente expresiones funcionales simbólicas, es convertirlas previamente a funciones numéricas y utilizar las funciones del paquete Matplotlib.

import numpy as np
import matplotlib.pyplot as plt

fnum = sp.lambdify(t,f)
tt = np.linspace(-4,4)
plt.figure(figsize=(6,4))
plt.plot(tt, fnum(tt))
plt.xlabel('t')
plt.title('Pulso rectangular')
plt.show()

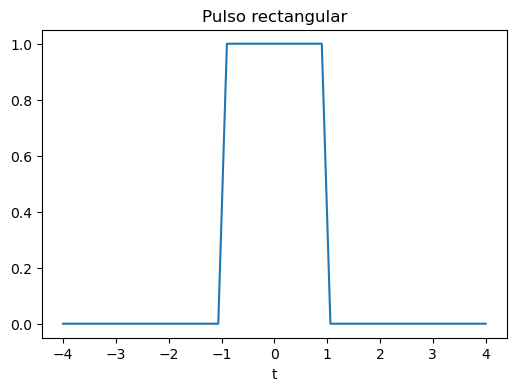
La transformada de Fourier podría calcularse y representarse gráficamente de forma muy fácil con ayuda de Python

t, w = sp.symbols('t,w')
Tf = sp.fourier_transform(f, t, w/(2*sp.pi))
Tf

\[\displaystyle \frac{2 \sin{\left(w \right)}}{w}\]

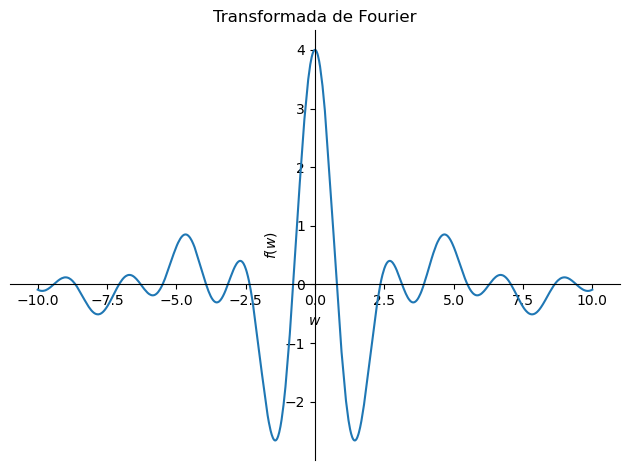
sp.plot(Tf,(w,-10,10), title='Transformada de Fourier del pulso rectangular');

---

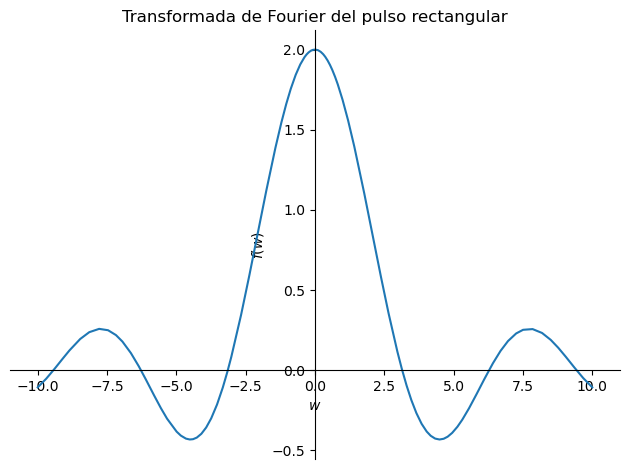
Ejemplo: transformada de Fourier de la función pulso triangular

La función pulso triangular puede definirse con ayuda de la función Piecewise() del paquete SymPy que define “funciones a trozos”

a = 2
f = sp.Piecewise( (0,     ((t<-a)|(t>a)) ),
                  (1+t/a, ((t>=-a)&(t<0)) ),
                  (1-t/a, ((t>=0)&(t<=a)) ))
f

\[\begin{split}\displaystyle \begin{cases} 0 & \text{for}\: t > 2 \vee t < -2 \\\frac{t}{2} + 1 & \text{for}\: t \geq -2 \wedge t < 0 \\1 - \frac{t}{2} & \text{for}\: t \geq 0 \wedge t \leq 2 \end{cases}\end{split}\]

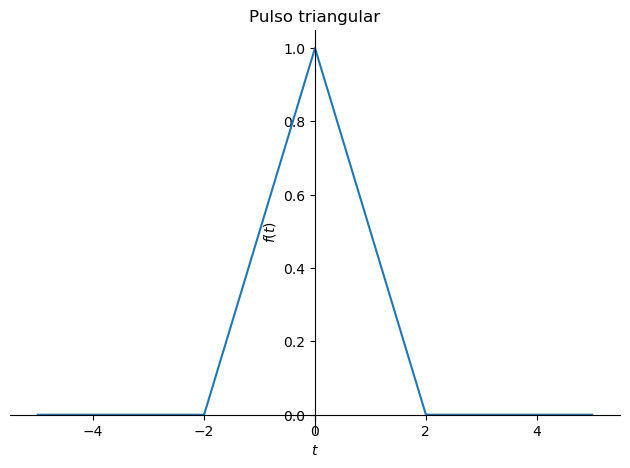
sp.plot(f, (t,-5,5), title='Pulso triangular');

Tf = sp.fourier_transform(f, t, w/(2*sp.pi)).simplify()
Tf

\[\begin{split}\displaystyle \begin{cases} \frac{\left(\left(2 - e^{2 i w}\right) e^{2 i w} - 1\right) e^{- 2 i w}}{2 w^{2}} & \text{for}\: w \neq 0 \\2 & \text{otherwise} \end{cases}\end{split}\]

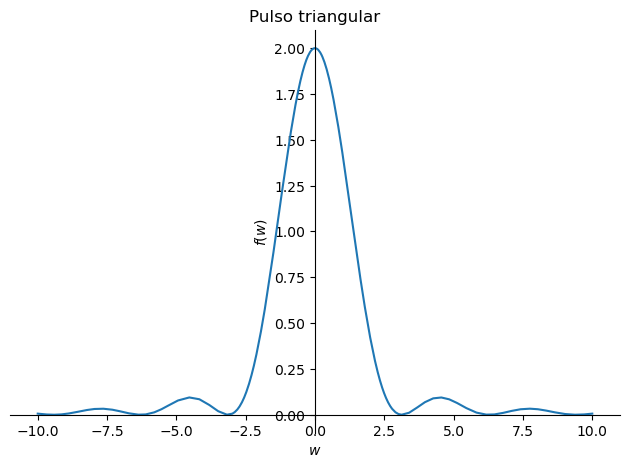
La transformada de Fourier de la función pulso triangular es

\[\frac{4\sin^2(wa/2)}{aw^2}\]

sp.plot(Tf, (w,-10,10), title='Pulso triangular');

---

Ejemplo:

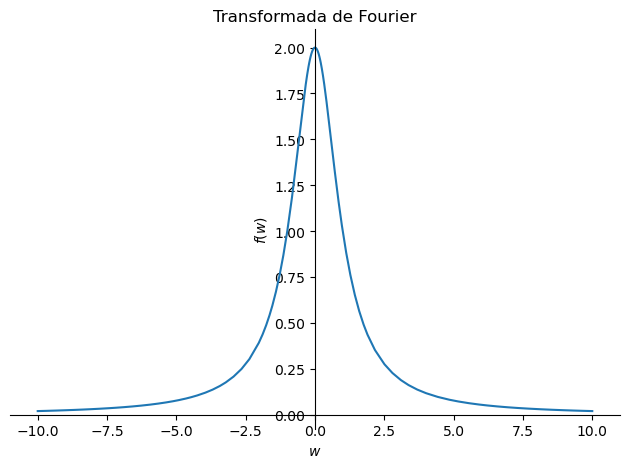
Transformada de Fourier de la función \(f(t)=e^{-|t|}\)

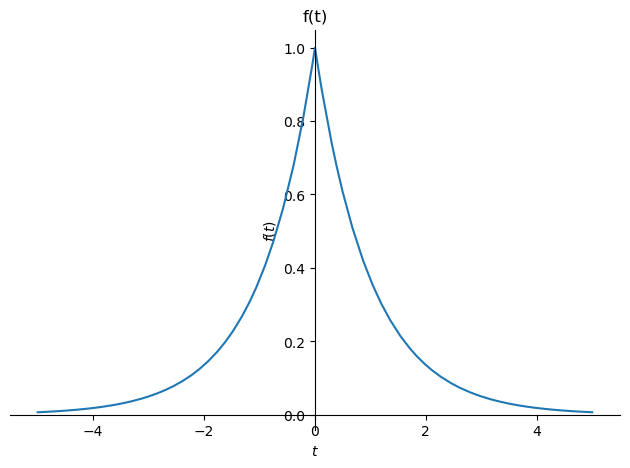
f = sp.exp(-sp.Abs(t))
sp.plot(f, (t,-5,5), title='f(t)')
Tf = sp.fourier_transform(f, t, w/(2*sp.pi)).simplify()
print('Transformada de Fourier:', Tf)
sp.plot(Tf, (w,-10,10), title='Transformada de Fourier');

Transformada de Fourier: 2/(w**2 + 1)

---

Ejemplo:

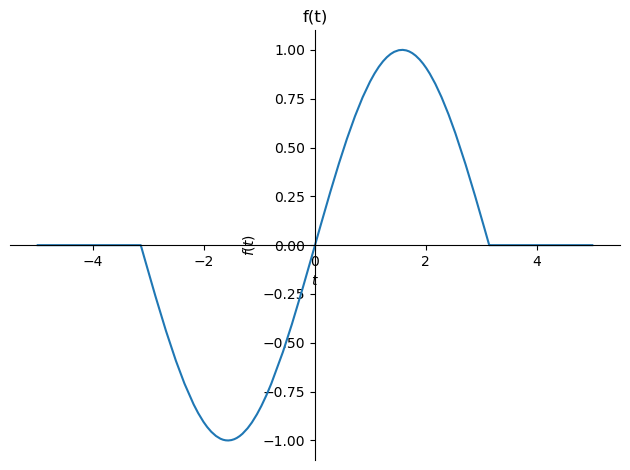
Transformada de Fourier de la función

\[\begin{split}f(t)=\left\{ \begin{array}{cc} \sin t & \mbox{si }|t|\leq \pi \\ 0 & \mbox{en otro caso} \end{array} \right.\end{split}\]

f = sp.Piecewise( (sp.sin(t), (sp.Abs(t)<=sp.pi) ),
                  (0, True))
sp.plot(f, (t,-5,5), title='f(t)')
sp.fourier_transform(f, t, w/(2*sp.pi)).simplify()

\[\begin{split}\displaystyle \begin{cases} \pi e^{\frac{i \pi}{2}} & \text{for}\: w = -1 \\\pi e^{- \frac{i \pi}{2}} & \text{for}\: w = 1 \\\frac{2 i \sin{\left(\pi w \right)}}{w^{2} - 1} & \text{otherwise} \end{cases}\end{split}\]

Se puede calcular la transformada realizando directamente la integral siguiente:

\[F(w)=F(f(t))(w)=\int_{-\infty}^{\infty} f(t)e^{-iwt}dt =\int_{-\pi}^{\pi} \sin(t)e^{-iwt}dt \]

Tf = sp.integrate(sp.sin(t)*sp.exp(-sp.I*w*t), (t, -sp.pi, sp.pi)).simplify()
Tf

\[\begin{split}\displaystyle \begin{cases} i \pi & \text{for}\: w = -1 \\- i \pi & \text{for}\: w = 1 \\\frac{2 i \sin{\left(\pi w \right)}}{w^{2} - 1} & \text{otherwise} \end{cases}\end{split}\]

---

Ejemplo:

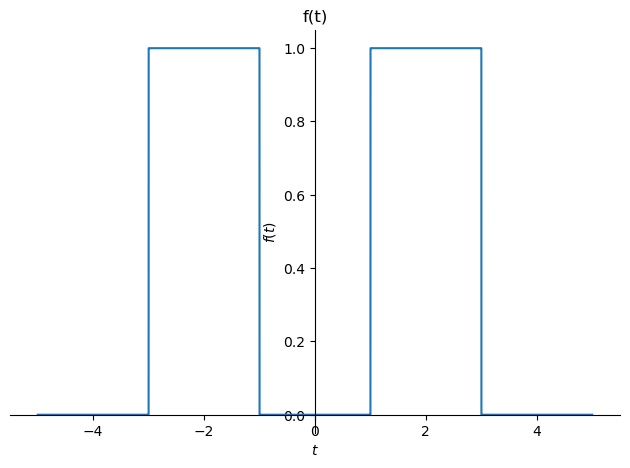
Transformada de Fourier de la función

\[\begin{split}f(t)=\left\{ \begin{array}{cc} 1 & \mbox{si }-3\leq t\leq -1 \\ 1 & \mbox{si } 1\leq t\leq 3 \\ 0 & \mbox{en otro caso}\\ \end{array} \right.\end{split}\]

f = sp.Piecewise( (1, ((-3<=t)&(t<=-1)) ),
                  (1, ((1<=t)&(t<=3)) ),
                  (0, True))

sp.plot(f, (t,-5,5), title='f(t)')
Tf = sp.fourier_transform(f, t, w/(2*sp.pi)).simplify()
print('Transformada de Fourier:', Tf)
sp.plot(Tf, (w,-10,10), title='Transformada de Fourier');

Transformada de Fourier: Piecewise((I*(-exp(6*I*w) + exp(4*I*w) - exp(2*I*w) + 1)*exp(-3*I*w)/w, Ne(w, 0)), (4, True))