Campos escalares y vectoriales

Otro concepto de gran importancia práctica es el de la integración de campos escalares y vectoriales a lo largo de curvas o superficies. Esta parte del curso se dedicará a estudiar estos conceptos, para ello es preciso dar previamente la definición del concepto de campo escalar y vectorial y unas nociones básicas de la parametrización de curvas en el plano y superficies en el espacio. Una vez presentados esos conceptos se mostrará la forma de calcular integrales de campos sobre curvas y superficies, junto con las principales propiedades y aplicaciones prácticas de los conceptos analizados.

Un campo es en general la distribución de una magnitud física cuyo valor depende del punto del plano o del espacio y del instante que se considere. Cuando el valor de esa magnitud física es igual en todos los puntos se dice que es uniforme. A los campos que son independientes del tiempo se les llama estacionarios, y son los que serán objeto de análisis en esta sección.

Campo escalar:

Cuando la magnitud física que define el campo necesita de un solo número para su caracterización, se dice que se trata de un campo escalar. De manera que un campo escalar en el plano se corresponde con una función de la forma

\[F:R^2\longrightarrow R\]

que asocia a cada punto \((x,y)\) del plano un valor real \(F(x,y)\) En el caso de campos escalares en el espacio, correspondería con una función de la forma

\[F:R^3\longrightarrow R\]

que asocia a cada punto \((x,y,z)\) el valor real \(F(x,y,z)\)

Ejemplos de campos escalares serían:

• Un campo escalar de temperaturas, que asigna a cada punto de un recinto, plano o tridimensional, el valor de la temperatura medida en ese punto.

• Campo de presiones atmosféricas en los distintos puntos de la superficie terrestre.

• Campo de alturas en un plano topográfico.

• Campo de densidad de población.

Campo vectorial:

Cuando la magnitud física requiere para su caracterización de una magnitud, una dirección y un sentido, se dice que se trata de un campo vectorial. Los campos vectoriales en el plano vienen determinados, por tanto, por una función

\[\vec{F}:R^2\longrightarrow R^2\]

que asocia a cada punto \((x,y)\) del plano un vector en la forma

\[\vec{F}(x,y)=(M(x,y),N(x,y))\]

siendo \(M\) y \(N\) dos funciones reales. En este caso, además de la notación anterior se utilizará la notación

\[\vec{F}(x,y)=M(x,y)\vec{i}+N(x,y)\vec{j}\]

Por otro lado, los campos vectoriales en el espacio vienen definidos por funciones de la forma \(\vec{F}:R^3\longrightarrow R^3\) que asocian a cada punto \((x,y,z)\) un vector del espacio en la forma

\[\vec{F}(x,y,z)=(F_1(x,y,z),F_2(x,y,z),F_3(x,y,z))\]

siendo \(F_1\), \(F_2\) y \(F_3\) funciones reales. En este caso además se utilizará la notación

\[\vec{F}(x,y,z)=F_1(x,y,z)\vec{i}+F_2(x,y,z)\vec{j}+F_3(x,y,z)\vec{k}\]

Ejemplos de campos vectoriales serían:

• Campo de velocidades en un fluido (por ejemplo, las velocidades del viento, el desplazamiento de un cuerpo flotante en el agua).

• Fuerzas en un campo electromagnético.

• Campo gradiente que señala las direcciones de crecimiento de una función.

• Campo gravitatorio que señala la fuerza de atracción ejercida por un sólido situado en un punto específico del espacio.

Definición de campos con el módulo Vector del paquete SymPy

Dentro del paquete SymPy de Python se encuentra implementado un módulo que facilita operaciones vectoriales y de cálculo diferencial. El módulo se denomina Vector y permite definir tanto campos escalares como vectoriales. Como todo paquete, la primera operación necesaria para su uso es la importación:

import sympy as sp
import sympy.vector as vec

Para definir campos se necesita como paso previo la definición de un sistema de coordenadas; el modulo permite trabajar con coordenadas cartesianas, pero también con coordenadas esféricas u otros sistemas de coordenadas personalizados.

Para definir el sistema de coordenadas cartesianas se utiliza la instrucción siguiente:

S = vec.CoordSys3D('')

A partir de ese momento quedan definidos tres vectores unitarios a los que se hará referencia usando el nombre asignado al sistema de referencia, en este caso S. En concreto, los tres vectores unitarios serán S.i, S.j y S.k y permitirán definir vectores a partir de sus coordenadas en el sistema de coordenadas cartesianas.

v = 2*S.i + 3*S.j + 5*S.k
w = -6*S.j + 2*S.k

v, w

(2*.i + 3*.j + 5*.k, (-6)*.j + 2*.k)

Con los vectores pueden realizarse las operaciones vectoriales básicas (suma y producto por escalar), pero también algunas otras operaciones habituales, como por ejemplo calcular el módulo del vector (magnitude) o productos escalares (dot) y vectoriales (cross)

v + 2*w

\[\displaystyle \left(2\right)\mathbf{\hat{i}_{}} + \left(-9\right)\mathbf{\hat{j}_{}} + \left(9\right)\mathbf{\hat{k}_{}}\]

v.magnitude()

\[\displaystyle \sqrt{38}\]

v.dot(w)

\[\displaystyle -8\]

v.cross(w)

\[\displaystyle \left(36\right)\mathbf{\hat{i}_{}} + \left(-4\right)\mathbf{\hat{j}_{}} + \left(-12\right)\mathbf{\hat{k}_{}}\]

w.cross(v)

\[\displaystyle \left(-36\right)\mathbf{\hat{i}_{}} + \left(4\right)\mathbf{\hat{j}_{}} + \left(12\right)\mathbf{\hat{k}_{}}\]

Utilizando el producto escalar es fácil extraer las componentes individuales de cualquier vector:

v.dot(S.i)

\[\displaystyle 2\]

v.dot(S.j)

\[\displaystyle 3\]

v.dot(S.k)

\[\displaystyle 5\]

Dado el sistema de coordenadas S, también quedarán definidas automáticamente las coordenadas cartesianas S.x, S.y y S.z, de manera que un punto \((x,y,z)\) se planteará con la notación (S.x,S.y,S.z), pudiéndose igualmente definir expresiones simbólicas a partir de las coordenadas cartesianas. De esta forma podrían definirse de forma simbólica tanto campos escalares como vectoriales. Utilizando la notación vectorial pueden definirse tanto campos escalares como vectoriales.

Por ejemplo, a continuación se definen dos campos tridimensionales, el primero el campo escalar

\[F(x,y,z)=x^2yz-3x+y\]

y el segundo el campo vectorial

\[\vec{G}(x,y,z)=(x+y+z)\vec{i}+(2y\,sen(xz))\vec{j}+(3xz^2+z)\vec{k}\]

F = S.x**2 * S.y * S.z - 3*S.x + S.y
F

\[\displaystyle \mathbf{{x}_{}}^{2} \mathbf{{y}_{}} \mathbf{{z}_{}} - 3 \mathbf{{x}_{}} + \mathbf{{y}_{}}\]

G = (S.x + S.y + S.z)*S.i + (2* S.y* sp.sin(S.x * S.z))*S.j + (3 * S.x * S.z**2 + S.z)*S.k
G

\[\displaystyle \left(\mathbf{{x}_{}} + \mathbf{{y}_{}} + \mathbf{{z}_{}}\right)\mathbf{\hat{i}_{}} + \left(2 \mathbf{{y}_{}} \sin{\left(\mathbf{{x}_{}} \mathbf{{z}_{}} \right)}\right)\mathbf{\hat{j}_{}} + \left(3 \mathbf{{x}_{}} \mathbf{{z}_{}}^{2} + \mathbf{{z}_{}}\right)\mathbf{\hat{k}_{}}\]

Sobre esos campos es posible utilizar las diferentes funciones de manipulación de expresiones simbólicas del paquete SymPy, en particular realizar procesos de derivación e integración simbólica.

sp.diff(F, S.x)

\[\displaystyle 2 \mathbf{{x}_{}} \mathbf{{y}_{}} \mathbf{{z}_{}} - 3\]

sp.diff(G, S.x)

\[\displaystyle \mathbf{\hat{i}_{}} + \left(2 \mathbf{{y}_{}} \mathbf{{z}_{}} \cos{\left(\mathbf{{x}_{}} \mathbf{{z}_{}} \right)}\right)\mathbf{\hat{j}_{}} + \left(3 \mathbf{{z}_{}}^{2}\right)\mathbf{\hat{k}_{}}\]

sp.integrate(F, S.x)

\[\displaystyle \frac{\mathbf{{x}_{}}^{3} \mathbf{{y}_{}} \mathbf{{z}_{}}}{3} - \frac{3 \mathbf{{x}_{}}^{2}}{2} + \mathbf{{x}_{}} \mathbf{{y}_{}}\]

sp.integrate(F, (S.x, 0 ,1), (S.y, 0, 2), (S.z, 0, 4))

\[\displaystyle \frac{4}{3}\]

La evaluación de los campos definidos simbólicamente sobre puntos concretos del espacio podría realizarse con ayuda de la función subs, que permite aplicar sustituciones. Por ejemplo \(F(1,2,2)\) y \(\vec{G}(1,2,2)\) se calcularían de la siguiente manera:

F.subs({S.x:1, S.y:2, S.z:2})

\[\displaystyle 3\]

G.subs({S.x:1, S.y:2, S.z:2})

\[\displaystyle \left(5\right)\mathbf{\hat{i}_{}} + \left(4 \sin{\left(2 \right)}\right)\mathbf{\hat{j}_{}} + \left(14\right)\mathbf{\hat{k}_{}}\]

Representación gráfica de campos

En ocasiones resulta interesante disponer de mecanismos de visualización gráfica de los campos. Especialmente en el caso de campos bidimensionales, esto se puede hacer de dos maneras:

• Representando la superficie tridimensional \(z=F(x,y)\)

• Mediante las conocidas como curvas de nivel, también conocidas como líneas equipotenciales, y que están formadas por los puntos del plano que tienen un mismo valor para el campo, es decir, las curvas de la forma

\[F(x,y)=c\]

Ambos tipos de representación pueden realizarse con ayuda del paquete Matplotlib de Pyhon, pero trabajando con versiones numéricas de los campos. A continuación se muestran algunos ejemplos.

---

Ejemplo:

El caso más simple corresponde a los campos lineales, es decir, de la forma \(F(x,y)=\alpha x+\beta y+\gamma\). Su representación tridimensional correspondería a un plano y sus curvas de nivel a una familia de rectas paralelas \(\alpha x+\beta y+\gamma=c\)

alfa, beta, gamma = 1, 2, 1
def F(x,y):return(alfa*x+beta*y+gamma)

import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_xlabel('x'); ax.set_ylabel('y')
x, y = np.meshgrid(np.linspace(0, 10), np.linspace(0, 10))
campo = ax.plot_surface(x, y, F(x,y), alpha=0.5, cmap='viridis')
fig.colorbar(campo, shrink=0.5, aspect=5)
plt.show()

plt.contourf(x, y, F(x,y), 15, alpha=0.5, cmap='viridis')
plt.show()

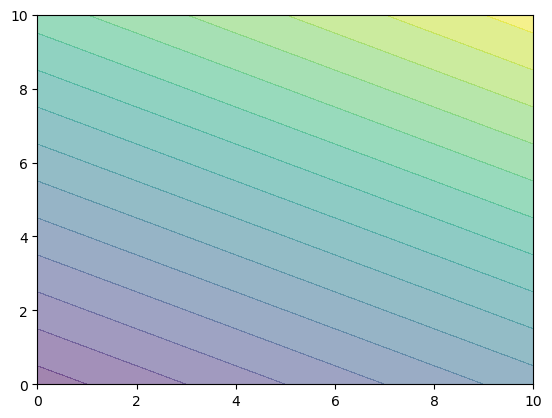
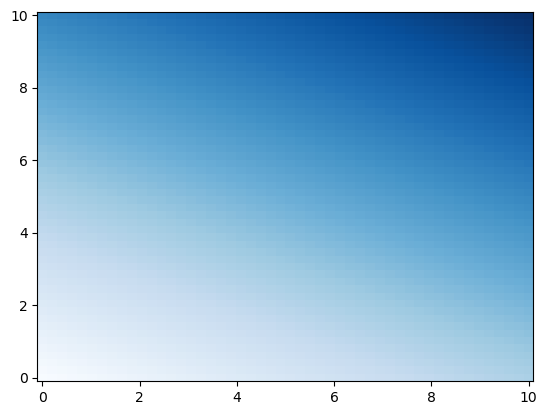
Otra alternativa es la utilización de la función pcolormesh también disponible en el paquete Matplotlib

plt.pcolormesh(x, y, F(x,y), cmap = 'Blues') 
plt.show()

---

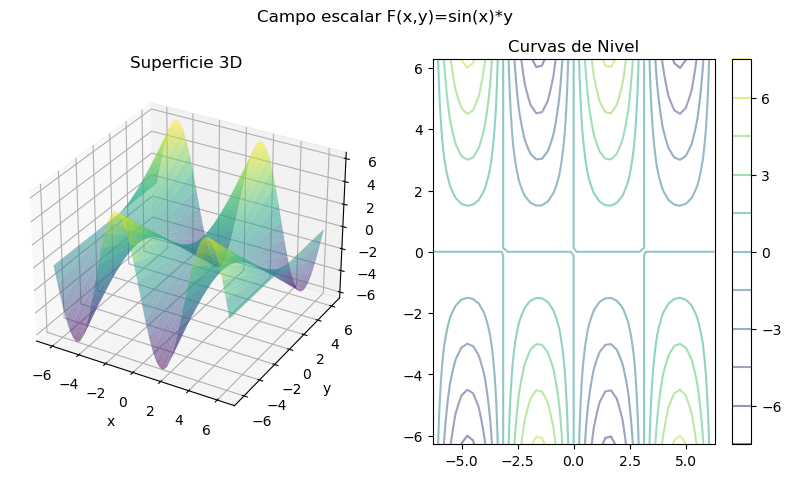
Ejemplo:

Para campos no lineales las representaciones gráficas pueden resultar más complejas, pero igualmente se podrían realizar con ayuda de Python.

def F(x,y):return(np.sin(x)*y)

x, y = np.meshgrid(np.linspace(-2*np.pi, 2*np.pi), np.linspace(-2*np.pi, 2*np.pi))
fig = plt.figure(figsize=(10,5))
fig.suptitle('Campo escalar F(x,y)=sin(x)*y')
# Subplot para la superficie 3D
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(x, y, F(x,y), alpha=0.5, cmap='viridis')
ax1.set_xlabel('x'); ax1.set_ylabel('y')
ax1.set_title('Superficie 3D')
# Subplot para las curvas de nivel
ax2 = fig.add_subplot(122)
cnivel = ax2.contour(x, y, F(x,y), 10, alpha=0.5, cmap='viridis')
ax2.set_title('Curvas de Nivel')
fig.colorbar(cnivel, ax=ax2, orientation='vertical')
plt.show()

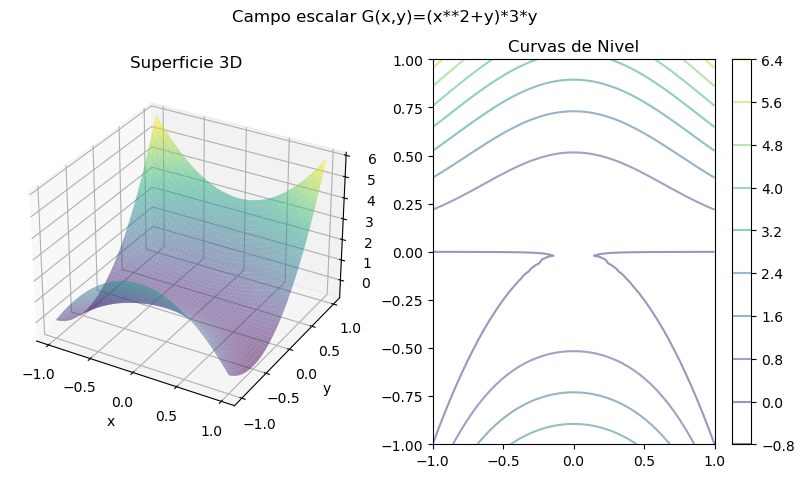
G = lambda x,y: (x**2+y)*3*y

x, y = np.meshgrid(np.linspace(-1,1), np.linspace(-1,1))
fig = plt.figure(figsize=(10,5))
fig.suptitle('Campo escalar G(x,y)=(x**2+y)*3*y')
# Subplot para la superficie 3D
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(x, y, G(x,y), alpha=0.5, cmap='viridis')
ax1.set_xlabel('x'); ax1.set_ylabel('y')
ax1.set_title('Superficie 3D')
# Subplot para las curvas de nivel
ax2 = fig.add_subplot(122)
cnivel = ax2.contour(x, y, G(x,y), 10, alpha=0.5, cmap='viridis')
ax2.set_title('Curvas de Nivel')
fig.colorbar(cnivel, ax=ax2, orientation='vertical')
plt.show()

H = lambda x,y: np.sin(x**2 + y**2)

x, y = np.meshgrid(np.linspace(-2,2), np.linspace(-2,2))
fig = plt.figure(figsize=(10,5))
fig.suptitle('Campo escalar H(x,y)=sin(X**2+Y**2)')
# Subplot para la superficie 3D
ax1 = fig.add_subplot(121, projection='3d')
ax1.plot_surface(x, y, H(x,y), alpha=0.5, cmap='viridis')
ax1.set_xlabel('x'); ax1.set_ylabel('y')
ax1.set_title('Superficie 3D')
# Subplot para las curvas de nivel
ax2 = fig.add_subplot(122)
cnivel = ax2.contour(x, y, H(x,y), 10, alpha=0.5, cmap='viridis')
ax2.set_title('Curvas de Nivel')
fig.colorbar(cnivel, ax=ax2, orientation='vertical')
plt.show()

---

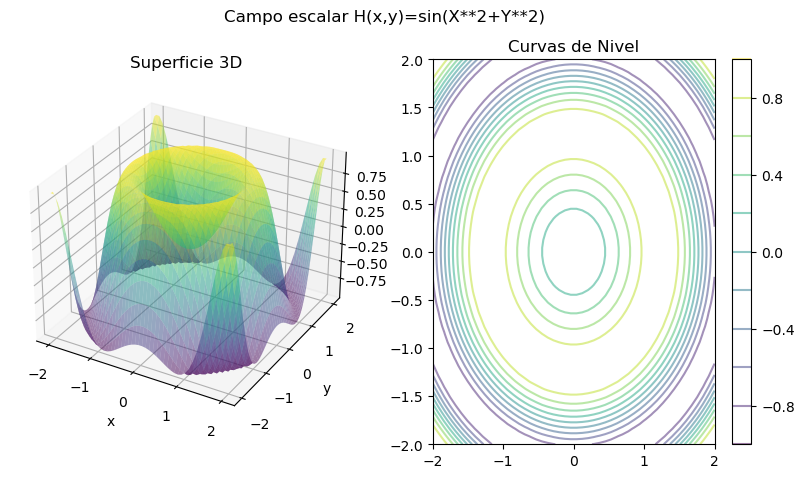
La representación gráfica de los campos escalares tridimensionales resulta mucho más compleja, ya que en lugar de curvas de nivel o líneas equipotenciales, se tendrían realmente superficies equipotenciales.

En el caso de los campos vectoriales, se suelen representar mediante un gráfico en el que a continuación de cada punto se representa el vector correspondiente. Un campo vectorial bidimensional se podría representar en el plano, pero un campo vectorial tridimensional debería representarse en el espacio.

La representación gráfica de campos vectoriales \(\vec{F}(x,y)=U(x,y)\vec{i}+V(x,y)\vec{j}\) con Python puede hacerse con la función quiver.

Por ejemplo, el campo homogéneo \(\vec{F}(x,y)=\vec{i}+2\vec{j}\) se representaría de la siguiente manera:

x,y = np.meshgrid(np.linspace(-5,5,10),np.linspace(-5,5,10))
u, v = 1, 2
plt.quiver(x,y,u,v)
plt.show()

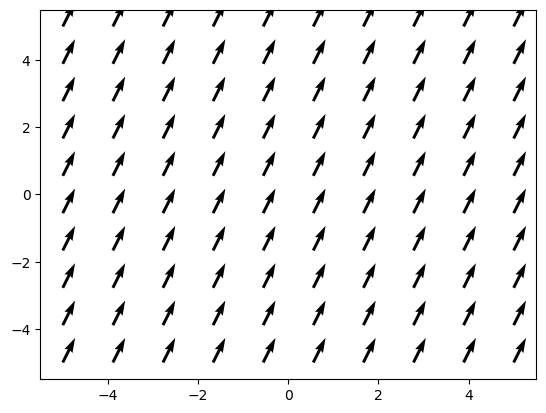
El campo anterior es un campo uniforme (valores constantes), por supuesto, también es posible representar campos en los que la magnitud vectorial cambia en cada punto del plano. Por ejemplo, el campo

\[\vec{F}(x,y)=\frac{x}{x^2+y^2}\vec{i}+\frac{y}{x^2+y^2}\vec{j}\]

x,y = np.meshgrid(np.linspace(-1,1,20),np.linspace(-1,1,20))
u, v = x/(x**2 + y**2), y/(x**2 + y**2)
plt.quiver(x,y,u,v)
plt.show()

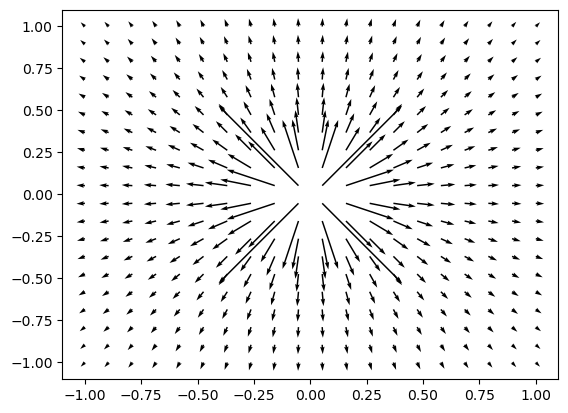
Otro ejemplo sería el campo \(\vec{F}(x,y)=\frac{-y}{\sqrt{x^2+y^2}}\vec{i}+\frac{x}{\sqrt{x^2+y^2}}\vec{j}\):

x,y = np.meshgrid(np.linspace(-5,5,20),np.linspace(-5,5,20))
u, v = -y/np.sqrt(x**2 + y**2), x/np.sqrt(x**2 + y**2)
plt.quiver(x,y,u,v)
plt.show()

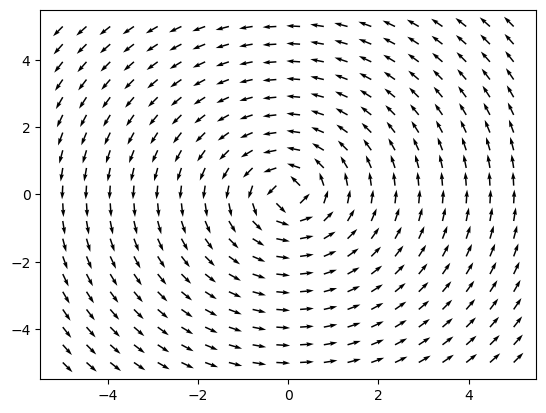
A continuación pueden verse la representación gráfica de otros cuatro campos vectoriales sencillos en el plano:

• \(x\vec{i}\)

• \(x\vec{i}+y\vec{j}\)

• \(-y\vec{i}+x\vec{j}\)

• \((x+y)\vec{i}+(x-y)\vec{j}\)

x, y = np.meshgrid(np.linspace(-1,1,15), np.linspace(-1,1,15))

fig = plt.figure(figsize=(10,10))
ax1 = fig.add_subplot(221)
plt.title('Campo (x,0)')
u,v  = x, np.zeros_like(x)
ax1.quiver(x,y,u,v)

ax1 = fig.add_subplot(222)
plt.title('Campo (x,y)')
u,v  = x, y
ax1.quiver(x,y,u,v)

ax1 = fig.add_subplot(223)
plt.title('Campo (-y,x)')
u,v  = -y, x
ax1.quiver(x,y,u,v)

ax1 = fig.add_subplot(224)
plt.title('Campo (x+y,x-y)')
u,v  = x+y, x-y
ax1.quiver(x,y,u,v)
plt.show()

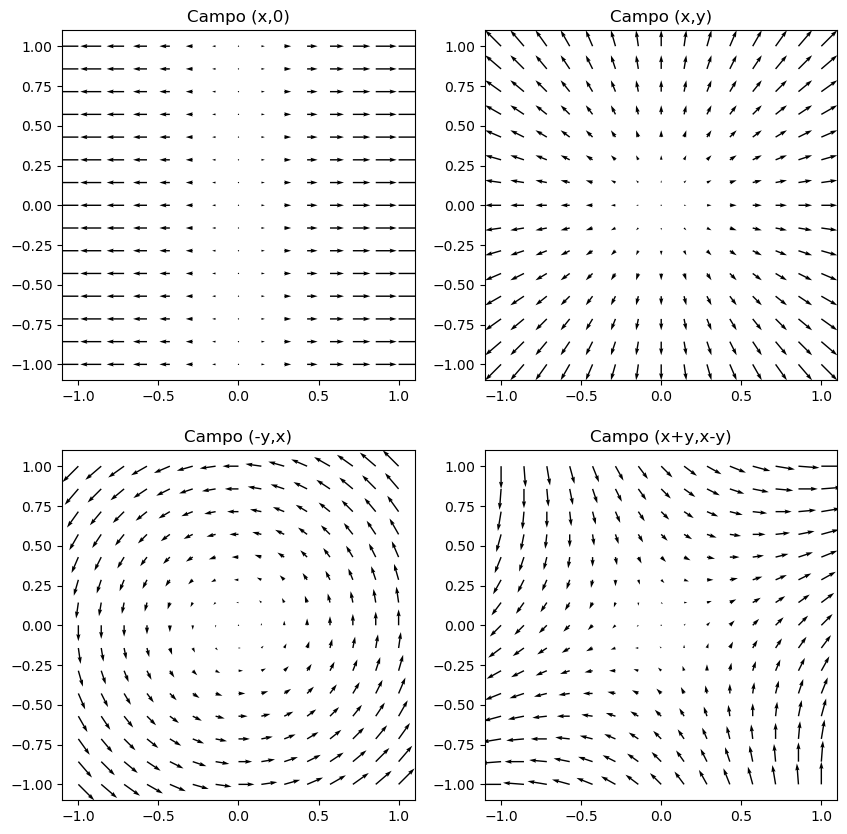
La representación gráfica de los campos vectoriales tridimensionales resulta más compleja, pero también puede realizarse con la misma función. Por ejemplo, si se considera el campo

\[\vec{F}(x,y,z)=(x+y-z)\vec{i}+y^2\vec{j}+(x-2yz)\vec{k}\]

su representación gráfica sería:

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_xlabel('x'); ax.set_ylabel('y')
x, y, z = np.meshgrid(np.linspace(-1,1,8),
                      np.linspace(-1,1,8),
                      np.linspace(-1,1,8))
u, v, w = x+y-z, y**2, x-2*y*z
ax.quiver(x,y,z,u,v,w, length=0.1)
plt.show()

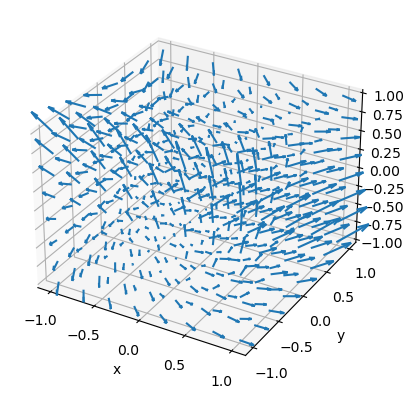
Otro ejemplo será el campo vectorial \(\vec{F}=x^2\vec{i}+y\vec{j}+2z\vec{k}\), cuya representación gráfica se obtiene con el siguiente código:

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_xlabel('x'); ax.set_ylabel('y')
x, y, z = np.meshgrid(np.linspace(-1,1,8),
                      np.linspace(-1,1,8),
                      np.linspace(-1,1,8))
u, v, w = x**2, y, 2*z
ax.quiver(x,y,z,u,v,w, length=0.1)
plt.show()

Los campos vectoriales también pueden ser visualizados utilizando las conocidas como líneas de flujo, que son líneas que en cada punto tienen por tangente el valor de campo en dicho punto. Estas líneas de flujo mostrarían la trayectoria que seguiría una partícula pequeña moviéndose en el campo entendiendo este como un campo de fuerzas.

Esta estrategia de representación mediante líneas de flujo puede utilizarse tanto para campos bidimensionales como tridimensionales, aunque de nuevo, resulta más sencilla de obtener y visualizar en campos del plano.

Dado el campo vectorial \(\sin y\,\vec{i}+x\vec{j}\) sus líneas de campo están definidas por la familia de curvas

\[\frac{x^2}{2}+\cos y=k\]

La representación gráfica de dicho campo vectorial junto con sus líneas de flujo pueden verse a continuación.

x, y = np.meshgrid(np.linspace(-1,1,10), np.linspace(-1,1,10))
u, v = np.sin(y), x
plt.quiver(x,y,u,v)
plt.streamplot(x,y,u,v)
plt.show()

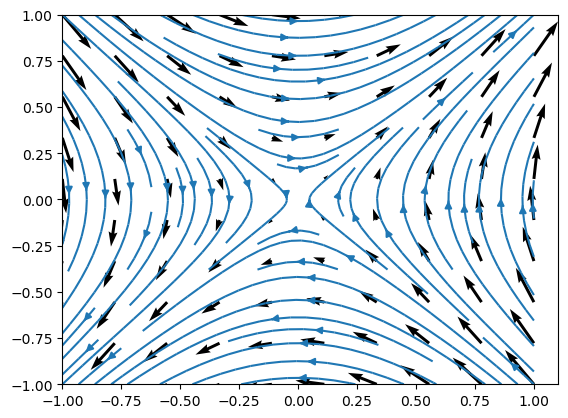
Algunos campos especiales: operadores diferenciales

Cuando se trabaja con campos definidos por funciones diferenciables pueden construirse una serie de campos con especiales aplicaciones prácticas y que se presentan brevemente a continuación.

En primer lugar, dado un campo escalar, cuando las curvas de nivel (o superficies en el caso de campos tridimensionales) están muy próximas entre sí se producen alteraciones bruscas en el valor del campo para puntos próximos. La magnitud que mide la máxima variación de la función escalar con la variación de la posición se denomina gradiente, siendo su sentido hacia los valores crecientes de la magnitud escalar que sufre la variación. El gradiente es una magnitud vectorial que opera sobre otra escalar, por tanto todo campo escalar lleva asociado un campo vectorial: su campo gradiente.

Campo gradiente:

Dada la función de un campo escalar \(F(x,y)\) diferenciable, el campo gradiente viene definido por:

\[\nabla F(x,y)=\left(\frac{\partial F}{\partial x}(x,y)\right)\vec{i}+ \left(\frac{\partial F}{\partial y}(x,y)\right)\vec{j}\]

En el caso de campos escalares tridimensionales, dado un campo \(F(x,y,z)\) diferenciable, su campo gradiente viene definido por:

\[\nabla F(x,y,z)=\left(\frac{\partial F}{\partial x}(x,y,z)\right)\vec{i}+ \left(\frac{\partial F}{\partial y}(x,y,z)\right)\vec{j}+ \left(\frac{\partial F}{\partial z}(x,y,z)\right)\vec{k}\]

El módulo de cálculo vectorial del paquete SymPy además de permitir definir los campos, dispone de funciones que permiten construir algunos campos especiales, entre ellos el campo gradiente. A continuación se muestra un ejemplo

---

Ejemplo:

Dado el campo escalar \(F(x,y)=x^3-3xy^2\), su campo gradiente es

\[\nabla F(x,y)=\left(\frac{\partial F}{\partial x}(x,y)\right)\vec{i}+ \left(\frac{\partial F}{\partial y}(x,y)\right)\vec{j} =(3x^2-3y^2)\vec{i}+(-6xy)\vec{j}\]

F = S.x**3 - 3 * S.x * S.y**2
vec.gradient(F)

\[\displaystyle \left(3 \mathbf{{x}_{}}^{2} - 3 \mathbf{{y}_{}}^{2}\right)\mathbf{\hat{i}_{}} + \left(- 6 \mathbf{{x}_{}} \mathbf{{y}_{}}\right)\mathbf{\hat{j}_{}}\]

Como ya se ha comentado, el campo gradiente de un campo escalar es siempre un campo vectorial. Además, la dirección del vector \(\nabla F\) siempre corresponde a la de máxima variación de la función escalar, siendo su sentido el correspondiente al sentido de crecimiento.

Por otro lado, en el caso de los campos en el plano el vector gradiente es siempre perpendicular a las curvas de nivel.

La representación gráfica de las curvas de nivel del campo escalar considerado y el campo gradiente asociado puede obtenerse en Python tal como se incluye a continuación. Además, en el gráfico generado se observa la perpendicularidad entre las curvas de nivel y el campo gradiente.

x, y = np.meshgrid(np.linspace(-10,10), np.linspace(-10,10))
plt.contourf(x, y, x**3-3*x*y**2, 15, alpha=0.5, cmap='viridis')
x, y = np.meshgrid(np.linspace(-10,10,15), np.linspace(-10,10,15))
u, v = 3*x**2-3*y**2, -6*x*y
plt.quiver(x,y,u,v)
plt.show()

---

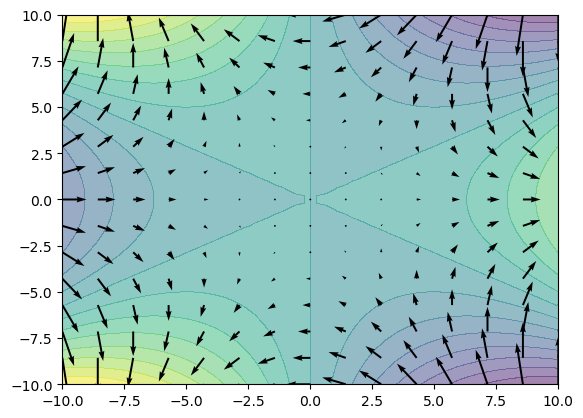
Todo campo vectorial diferenciable tiene a su vez asociado un campo escalar, conocido como divergencia, y que tiene importantes propiedades desde un punto de vista físico y matemático. La divergencia se define de la siguiente manera.

Campo divergencia:

Dado el campo vectorial \(\vec{F}(x,y)=M(x,y)\vec{i}+N(x,y)\vec{j}\) su divergencia es

\[div \vec{F}(x,y)=\frac{\partial M}{\partial x}(x,y)+ \frac{\partial N}{\partial y}(x,y)\]

En el caso de campos tridimensionales, si \(\vec{F}(x,y,z)\) es un campo vectorial diferenciable, su divergencia viene definida por:

\[div\, \vec{F}(x,y,z)=\left(\frac{\partial F_1}{\partial x}(x,y,z)\right)+ \left(\frac{\partial F_2}{\partial y}(x,y,z)\right)+ \left(\frac{\partial F_3}{\partial z}(x,y,z)\right)\]

La divergencia \(div(\vec{F})=\frac{\partial F_1}{\partial x}+\frac{\partial F_2}{\partial y}+\frac{\partial F_3}{\partial z}\) de un campo vectorial \(\vec{F}\) se puede calcular con la función divergence() del módulo Vector del paquete SymPy.

---

Ejemplo:

La divergencia del campo \(\vec{H}(x,y,z)=x^2\vec{i}+(x+y+z)\vec{j}+2yz^2\vec{k}\) sería:

H = (S.x**2)*S.i + (S.x+S.y+S.z)*S.j + (2*S.y*S.z**2)*S.k
vec.divergence(H)

\[\displaystyle 2 \mathbf{{x}_{}} + 4 \mathbf{{y}_{}} \mathbf{{z}_{}} + 1\]

---

Los campos con divergencia nula son conocidos como solenoidales y en el módulo se cuenta con una función para comprobar directamente si un campo tiene esa propiedad:

vec.is_solenoidal(H)

False

La divergencia también se puede calcular en Python sobre campos bidimensionales. Por ejemplo, la divergencia de \(\vec{F}(x,y)=(x^2+y)\vec{i}+(2xy^2)\vec{j}\) sería:

F = (S.x**2 + S.y)*S.i + (2 * S.x * S.y**2)*S.j
vec.divergence(F)

\[\displaystyle 4 \mathbf{{x}_{}} \mathbf{{y}_{}} + 2 \mathbf{{x}_{}}\]

Otro campo de gran importancia física es el conocido como rotacional, que puede ser aplicado sobre campos escalares y vectoriales. En este caso la definición de rotacional, y su interpretación, es diferente dependiendo de si se trata de un campo plano o tridimensional. Se comienza por definir el concepto en el caso de campos planos.

Rotacional de un campo escalar plano:

El rotacional de un campo escalar \(F(x,y)\) es un campo vectorial definido por

\[rot\;F(x,y)=\frac{\partial F}{\partial y}(x,y)\vec{i}-\frac{\partial F}{\partial x}(x,y)\vec{j}\]

---

Ejemplo:

Dado el campo escalar \(F(x,y)=\sin(2x+3y)\) su rotacional es:

\[rot\;F(x,y)=3\cos(2x+3y)\,\vec{i}-2\cos(2x+3y)\,\vec{j}\]

---

Rotacional de un campo vectorial plano:

El rotacional de un campo vectorial \(\vec{F}(x,y)=M(x,y)\vec{i}+N(x,y)\vec{j}\) es un campo escalar definido por:

\[rot\;\vec{F}(x,y)=\frac{\partial N}{\partial x}(x,y)-\frac{\partial M}{\partial y}(x,y)\]

A continuación se define el concepto para el caso de campos vectoriales tridimiensionales.

Rotacional de un campo vectorial tridimensional:

Dado un campo vectorial \(\vec{F}(x,y,z)\) diferenciable, su rotacional viene definido por:

\[\begin{split}\begin{array}{ccc} rot\, \vec{F}(x,y,z) & = & \left(\frac{\partial F_3}{\partial y}(x,y,z)-\frac{\partial F_2}{\partial z}(x,y,z)\right)\vec{i} \\ & + & \left(\frac{\partial F_1}{\partial z}(x,y,z)-\frac{\partial F_3}{\partial x}(x,y,z)\right)\vec{j} \\ & + & \left(\frac{\partial F_2}{\partial x}(x,y,z)-\frac{\partial F_1}{\partial y}(x,y,z)\right)\vec{k} \end{array}\end{split}\]

La expresión anterior también puede escribirse, de forma simbólica, como

\[\begin{split}rot\, \vec{F}(x,y,z)= \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ F_1 & F_2 & F_3 \\ \end{array} \right|\end{split}\]

El rotacional de un campo vectorial tridimensional, es por tanto un nuevo campo vectorial.

En el caso concreto de campos vectoriales bidimensionales, la definición de rotacional bidimensional coincide con la tercera componente del rotacional tridimensional equivalente.

El rotacional de un campo tridimensional es un nuevo campo vectorial que representa la componente de rotación del campo, su dirección determina el eje de rotación y su magnitud es el doble de la velocidad angular.

El módulo Vector de SymPy dispone de la función curl para el cálculo de rotacionales, pero únicamente se puede aplicar sobre campos vectoriales tridimensionales.

---

Ejemplo:

El rotacional del campo \(\vec{H}(x,y,z)=x^2\vec{i}+(x+y+z)\vec{j}+2yz^2\vec{k}\) sería:

\[\begin{split}rot\, \vec{F}(x,y,z)= \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ x^2 & x+y+z & 2yz^2 \end{array} \right| = (2z^2-1)\vec{i}+\vec{k} \end{split}\]

H = (S.x**2)*S.i + (S.x+S.y+S.z)*S.j + (2*S.y*S.z**2)*S.k
vec.curl(H)

\[\displaystyle \left(2 \mathbf{{z}_{}}^{2} - 1\right)\mathbf{\hat{i}_{}} + \mathbf{\hat{k}_{}}\]

---

Todos los operadores diferenciales que definen los campos anteriores son lineales, así por ejemplo, la divergencia de la suma de dos campos es la suma de las respectivas divergencias. Lo mismo ocurre con los gradientes o los rotacionales.

Haciendo uso del operador simbólico \(\nabla=\left(\frac{\partial}{\partial x},\frac{\partial}{\partial y},\frac{\partial}{\partial z}\right)\), la divergencia y el rotacional podrían expresarse en la forma:

\[\begin{split}\begin{array}{l} div\,\vec{F} = \nabla\cdot\vec{F} \\ rot\,\vec{F} = \nabla\times\vec{F} \end{array}\end{split}\]

---

Ejemplo:

Dado el campo vectorial

\[\vec{F}(x,y,z)=(2x^2+yz)\vec{i}+(x-z^2)\vec{j}+(2x+3yz^2)\vec{k}\]

Su divergencia y rotacional serían:

\[div\,\vec{F} = 4x+6yz\]

\[\begin{split}rot\, \vec{F}(x,y,z)= \left| \begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ \frac{\partial}{\partial x} & \frac{\partial}{\partial y} & \frac{\partial}{\partial z} \\ 2x^2+yz & x-z^2 & 2x+3yz^2 \\ \end{array} \right|= (3z^2+2z)\vec{i}+(y-2)\vec{j}+(1-z)\vec{k}\end{split}\]

tal como puede comprobarse también con Python:

F1 = 2 * S.x**2 + S.y * S.z
F2 = S.x - S.z**2
F3 = 2 * S.x + 3 * S.y * S.z**2
F = F1*S.i + F2*S.j + F3*S.k

vec.divergence(F)

\[\displaystyle 4 \mathbf{{x}_{}} + 6 \mathbf{{y}_{}} \mathbf{{z}_{}}\]

vec.curl(F)

\[\displaystyle \left(3 \mathbf{{z}_{}}^{2} + 2 \mathbf{{z}_{}}\right)\mathbf{\hat{i}_{}} + \left(\mathbf{{y}_{}} - 2\right)\mathbf{\hat{j}_{}} + \left(1 - \mathbf{{z}_{}}\right)\mathbf{\hat{k}_{}}\]

---

Aquellos campos cuyo rotacional el nulo se llaman campos conservativos y más adelante se irán descubriendo algunas de sus propiedades interesantes a efectos del cálculo integral. Una primera característica de estos campos es que cuentan con lo que se conoce como funciones potenciales. Una función \(f(x,y,z)\) es una función potencial de un campo conservativo \(\vec{F}(x,y,z)\) si cumple

\[\nabla f(x,y,z)=\vec{F}(x,y,z)\]

La condición de ser conservativo, es decir, tener un rotacional nulo, es necesaria para poder calcular una función potencial. Además, dado un campo conservativo el número de funciones potenciales es infinito, distinguiéndose unas de otras por una constante arbitraria.

En SymPy se cuenta con una función para determinar si un campo es conservativo (is_conservative()) y, en caso que lo sea, con otra que calcula una función potencial (scalar_potential()). Esta función recibe dos argumentos: el campo conservativo y el sistema de coordenadas.

---

Ejemplo:

De los dos campos siguientes uno es conservativo y el otro no:

\[\vec{G}(x,y,z)=(y^2cos(x)+z^3)\vec{i}+(2y\,sen(x)-4)\vec{j}+(3xz^2+z)\vec{k}\]

\[\vec{H}(x,y,z)=x^2\vec{i}+(x+y+z)\vec{j}+2yz^2\vec{k}\]

Se puede comprobar fácilmente con la función is_conservative:

G = (S.y**2*sp.cos(S.x)+S.z**3)*S.i + (2*S.y*sp.sin(S.x)-4)*S.j + (3*S.x*S.z**2+S.z)*S.k
H = (S.x**2)*S.i + (S.x+S.y+S.z)*S.j + (2*S.y*S.z**2)*S.k

vec.is_conservative(G)

True

vec.is_conservative(H)

False

Se puede comprobar que efectivamente el rotacional de la primera función es nulo, mientras que el de la segunda no lo es:

vec.curl(G)

\[\displaystyle \mathbf{\hat{0}}\]

vec.curl(H)

\[\displaystyle \left(2 \mathbf{{z}_{}}^{2} - 1\right)\mathbf{\hat{i}_{}} + \mathbf{\hat{k}_{}}\]

En el caso del campo conservativo, se podría calcular una función potencial; algo que generaría un error en el caso de la segunda función.

vec.scalar_potential(G, S)

\[\displaystyle \mathbf{{x}_{}} \mathbf{{z}_{}}^{3} + \mathbf{{y}_{}}^{2} \sin{\left(\mathbf{{x}_{}} \right)} - 4 \mathbf{{y}_{}} + \frac{\mathbf{{z}_{}}^{2}}{2}\]

Ejercicios propuestos

• Representar gráficamente las curvas de nivel de los campos escalares siguientes:

  \[F_1(x,y)=x-y\]
  \[F_2(x,y)=x-y^2+2y\]
  \[F_3(x,y)=xy\]

• Representar gráficamente los campos vectoriales siguientes:

  \[\vec{F_1}(x,y)=y\vec{i}+2\vec{j}\]
  \[\vec{F_2}(x,y)=x^2\vec{i}-y\vec{j}\]
  \[\vec{F_3}(x,y)=xy\vec{i}+2x\vec{j}\]

• Dado el campo escalar \(F(x,y)=xy-2x\) calcular su campo gradiente y representar en un mismo gráfico dicho campo junto con las curvas de nivel del campo escalar, comprobando la propiedad de ortogonalidad entre ambos.

• Comprobar que dado un campo escalar \(F(x,y)\) de clase \(C^2\) el rotacional de su campo gradiente es nulo.

• Calcular la divergencia y el rotacional de los siguientes campos vectoriales:

  \[\vec{F_1}(x,y)=x\vec{i}+y\vec{j}\]
  \[\vec{F_2}(x,y)=\sin x\,\vec{i}+\cos y\,\vec{j}\]
  \[\vec{F_3}(x,y)=x^2\vec{i}+xy\vec{j}\]

• Calcular los valores de \(a\) y \(b\) que hacen que el siguiente campo tenga un rotacional nulo

\[\vec{F}=axy\vec{i}+(x^2+z^3)\vec{j}+(byz^2-4z^3)\vec{k}\]

• Dado el campo vectorial \(\vec{F}=x\vec{i}+y\vec{j}+z\vec{k}\), se define el campo escalar \(G(x,y,z)=\|\vec{F}\|=\sqrt{x^2+y^2+z^2}\). Calcular el gradiente de \(G\) y el rotacional de \(\vec{F}\).