Aplicaciones de la integración triple

Cálculo de volúmenes

Si se considera una función \(f(x,y,z)=1\), la integral triple de dicha función sobre un sólido \(R\) coincide con el volumen de dicho sólido:

\[Volumen(R)=\iiint_R dV\]

---

Ejemplo:

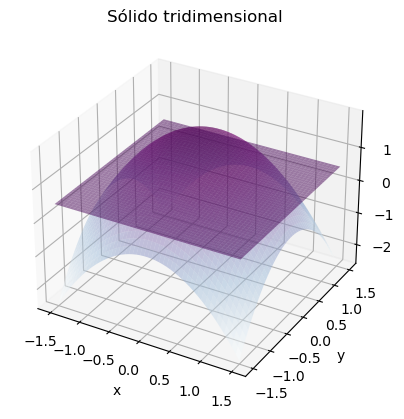
Se desea calcular el volumen del sólido \(R\) comprendido entre el paraboloide \(z=2-x^2-y^2\) y el plano horizontal \(z=1/2\). Dicho sólido puede verse a continuación:

import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Sólido tridimensional')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
x, y = np.meshgrid(np.linspace(-1.5, 1.5), np.linspace(-1.5, 1.5))
ax.plot_surface(x, y, 2-x**2-y**2, alpha=0.5, cmap='BuPu')
ax.plot_surface(x, y, 1/2*np.ones_like(x), alpha=0.5, cmap='viridis')
plt.show()

Para calcular dicho volumen habría que obtener el valor de la integral

\[\iiint_R dV\]

y para ello en este caso es recomendable el paso a coordenadas cilíndricas:

\[\begin{split}\begin{array}{l} x = r\cos\theta \\ y = r\sin\theta \\ z = z \end{array}\end{split}\]

siendo el Jacobiano de este cambio \(J=r\).

La variable \(z\) representa la altura sobre el sólido, por tanto variará entre \(1/2\) y \(2\). Fijado el valor de \(z\), la sección transversal del sólido correspondería a una circunferencia de radio \(\sqrt{2-z}\), por tanto la variable \(\theta\) variará entre \(0\) y \(2\pi\), y la \(r\) entre \(0\) y \(\sqrt{2-z}\). En definitiva, la integral que permite calcular el volumen es:

\[Volumen(R) = \int_{1/2}^2\int_0^{2\pi}\int_0^{\sqrt{2-z}}r \,dr\,d\theta\,dz\]

\[ =\int_{1/2}^2\int_0^{2\pi}\frac{2-z}{2}\,d\theta\,dz\]

\[=\int_{1/2}^2 \pi(2-z)\,dz =\left. \pi(2z-\frac{z^2}{2})\right|_{1/2}^2=\frac{9}{8}\pi\]

import sympy as sp
x,y,z,r,theta = sp.symbols('x,y,z,r,theta')
x = r*sp.cos(theta)
y = r*sp.sin(theta)
z = z
J = sp.Matrix([[sp.diff(x,r),sp.diff(x,theta),sp.diff(x,z)],
               [sp.diff(y,r),sp.diff(y,theta),sp.diff(y,z)],
               [sp.diff(z,r),sp.diff(z,theta),sp.diff(z,z)]]).det()
F = 1
sp.integrate(F*J, (r,0,sp.sqrt(2-z)), (theta,0,2*sp.pi), (z,1/2,2))

\[\displaystyle 1.125 \pi\]

---

Ejemplo:

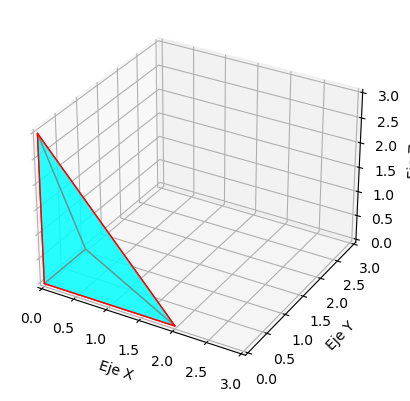
Se desea calcular el volumen del tetraedro que tiene como vértices los puntos \((0, 0, 0)\), \((0, 1, 0)\), \((2, 0, 0)\) y \((0, 0, 3)\), y que puede visualizarse de la siguiente manera:

from mpl_toolkits.mplot3d.art3d import Poly3DCollection
vertices = [[0, 0, 0],[0, 1, 0],[2, 0, 0],[0, 0, 3]]
caras = [
        [vertices[0], vertices[1], vertices[2]],
        [vertices[0], vertices[1], vertices[3]],
        [vertices[0], vertices[2], vertices[3]],
        [vertices[1], vertices[2], vertices[3]]
        ]
tetraedro = Poly3DCollection(caras, facecolors='cyan', linewidths=1, edgecolors='r',alpha=0.6)
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.add_collection3d(tetraedro)
ax.set_xlim([0, 3]); ax.set_xlabel('Eje X')
ax.set_ylim([0, 3]); ax.set_ylabel('Eje Y')
ax.set_zlim([0, 3]); ax.set_zlabel('Eje Z')
plt.show()

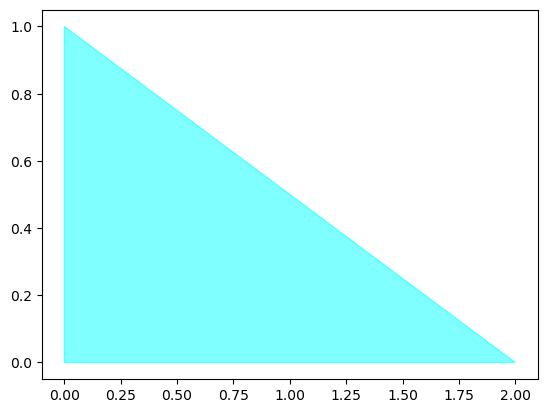
x,y,z = zip(*vertices)
plt.fill(x, y, color='cyan', alpha=0.5);

# ecuación de la recta que pasa por (0,1) y (2,0)
x1,y1 = 0,1
x2,y2 = 2,0
m = (y2 - y1) / (x2 - x1)
b = y1 - m * x1
ecuacion_recta = f"y = {m:.2f}x + {b:.2f}"
print(ecuacion_recta)

y = -0.50x + 1.00

A la vista de esa ecuación ya se podrían determinar los límites de variación de \(x\) e \(y\): \(0\leq x\leq 2\), \(0\leq y\leq 1-0.5x\). Para determinar el intervalo de variación de la \(z\) se tendría que calcular la ecuación del plano que determinan los vértices \((0, 1, 0)\), \((2, 0, 0)\) y \((0, 0, 3)\)

v1 = np.array(vertices[2])-np.array(vertices[1])
v2 = np.array(vertices[3])-np.array(vertices[1])
normal = np.cross(v1, v2)
A, B, C = normal
D = np.vdot(vertices[1],normal)
# ecuación del plano
ecuacion = f"{A:.2f}x + {B:.2f}y + {C:.2f}z = {D:.2f}"
print(ecuacion)

-3.00x + -6.00y + -2.00z = -6.00

A la vista de la ecuación de ese plano, los límites de integración de \(z\) serían \(0\leq z\leq(6-3x-6y)/2\), y por tanto, el volumen del tetraedro se calcularía con la siguiente integral:

import sympy as sp
x,y,z = sp.symbols('x,y,z')
sp.integrate(1, (z,0,(6-3*x-6*y)/2), (y,0,1-x/2), (x,0,2))

\[\displaystyle 1\]

Cálculo de masas y centros de masa

Al igual que ocurría en el caso de placas planas con densidades superficiales variables, si se tiene un sólido \(R\) cuya densidad en cada punto \((x,y,z)\) viene dada por una función \(\delta(x,y,z)\), se podría calcular la masa total del sólido mediante la integral:

\[Masa(R)=\iiint_R \delta(x,y,z)dV\]

Una vez calculada la masa, el centro de masas \((\bar{x},\bar{y},\bar{z})\) del sólido \(R\) puede calcularse también mediante las integrales

\[\begin{split}\begin{array}{l} \bar{x} = \frac{1}{Masa(R)}\iiint_R x\delta(x,y,z)dV\\ \bar{y} = \frac{1}{Masa(R)}\iiint_R y\delta(x,y,z)dV \\ \bar{z} = \frac{1}{Masa(R)}\iiint_R z\delta(x,y,z)dV \end{array}\end{split}\]

---

Ejemplo:

Se calcula a continuación la masa y el centro de masas de un cubo \(R=[0,1]\times[0,1]\times[0,1]\) con densidad en cada punto proporcional a la distancia del punto al plano \(0XY\), es decir, \(\delta(x,y,z)=kz\).

En primer lugar, la masa del cubo sería:

\[Masa(R)=\iiint_R kz\,dV =k\int_0^1\int_0^1\int_0^1 z\,dz\,dy\,dx= k\int_0^1\int_0^1\frac{1}{2}\,dz\,dy\,dx =\frac{k}{2}\]

El centro de masas vendría dado por el punto de coordenadas:

\[\begin{split}\begin{array}{l} \bar{x} &=& \frac{2}{k}\iiint_R xkz\,dV=2\iiint_R xz\,dV=\frac{1}{2}\\ \bar{y} &=& \frac{2}{k}\iiint_R ykz\,dV=2\iiint_R yz\,dV=\frac{1}{2}\\ \bar{z} &=& \frac{2}{k}\iiint_R kz^2\,dV=2\iiint_R z^2\,dV=\frac{2}{3} \end{array}\end{split}\]

x,y,z,k = sp.symbols('x,y,z,k')
densidad = k*z
masa = sp.integrate(densidad, (x,0,1), (y,0,1), (z,0,1))
cx = sp.integrate(x*densidad, (x,0,1), (y,0,1), (z,0,1))/masa
cy = sp.integrate(y*densidad, (x,0,1), (y,0,1), (z,0,1))/masa
cz = sp.integrate(z*densidad, (x,0,1), (y,0,1), (z,0,1))/masa
print('Masa:',masa)
print('Centro de masas:',cx,cy,cz)

Masa: k/2
Centro de masas: 1/2 1/2 2/3

---

Ejemplo:

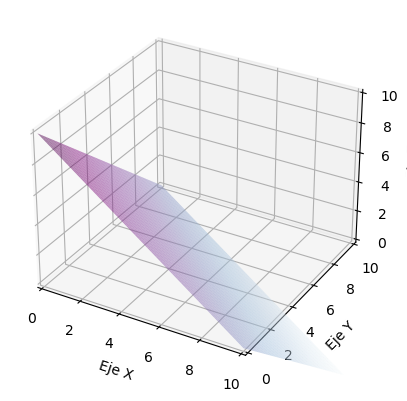
Se desea calcular la masa del sólido tridimensional que se encuentra entre los planos cartesianos y el plano \(x+y+z=10\), asumiendo una densidad constante \(\delta=3\). Para ello se tendría que calcular la integral

\[\iiint_R3dV = \int_{0}^{10}\int_{0}^{10-x}\int_{0}^{10-x-y}3 dz\,dy\,dx\]

Esta integral puede realizarse en Python tanto de manera simbólica como numérica. En el caso de optar por la integración numérica la única precaución es tener en cuenta el orden de las variables en la definición de la función.

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_xlim([0, 10]); ax.set_xlabel('Eje X')
ax.set_ylim([0, 10]); ax.set_ylabel('Eje Y')
ax.set_zlim([0, 10]); ax.set_zlabel('Eje Z')
x, y = np.meshgrid(np.linspace(0,10), np.linspace(0,10))
ax.plot_surface(x, y, 10-x-y, alpha=0.5, cmap='BuPu')
plt.show()

x,y,z = sp.symbols('x,y,z')
sp.integrate(3, (z,0,10-x-y), (y,0,10-x), (x,0,10))

\[\displaystyle 500\]

Esa misma integral podría resolverse numéricamente, pero con la precaución en el orden de las variables a la hora de definir la función y la integral:

from scipy import integrate
f = lambda z,y,x: 3
a = 0
b = 10
g = lambda x: 0
h = lambda x: 10-x
q = lambda x,y: 0
r = lambda x,y: 10-x-y
integrate.tplquad(f, a, b, g, h, q, r)

(500.0, 5.551115123125783e-12)

Cálculo de momentos de inercia

El momento de inercia del sólido \(R\) con respecto a un eje viene dado por

\[I_r=\iiint_R d(x,y,z)^2\delta(x,y,z)dV\]

donde \(\delta(x,y,z)\) es la función densidad y \(d(x,y,z)\) la distancia del punto \((x,y,z)\) al eje. Así, si se considera como eje el \(OZ\), el momento de inercia, trabajando en coordenadas cartesianas, sería:

\[I_z=\iiint_R (x^2+y^2)\delta(x,y,z)dV\]

En el caso de coordenadas cilíndricas, el momento de inercia con respecto al eje \(OZ\) es:

\[I_z=\iiint_R r^2\delta(x,y,z)dV\]

En el caso concreto de los momentos de inercia con respecto a los ejes \(0X\) y \(0Y\), éstos serían:

\[I_x=\iiint_R (y^2+z^2)\delta(x,y,z)dV;\;\;\;\;\; I_y=\iiint_R (x^2+z^2)\delta(x,y,z)dV\]

---

Ejemplo:

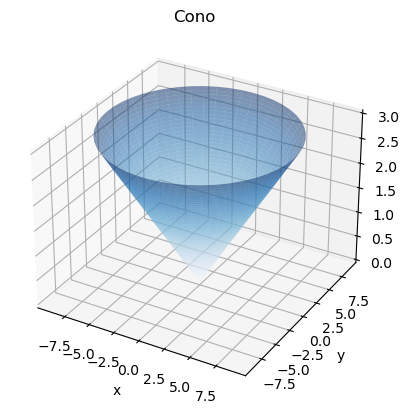
Considérese el cono de densidad homogénea \(\delta\) que viene definido en coordenadas cilíndricas por \(ar\leq z\leq b\). Ese cono viene delimitado por la superficie definida por la ecuación implícita \(x^2+y^2=z^2\) con \(z\in[0,b]\), o las ecuaciones paramétricas \(x=ar\cos\theta; y=ar\sin\theta; z=ar\). Por ejemplo, para el caso \(a=b=3\) el cono puede visiualizarse de la siguiente manera:

a, b = 3, 3
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Cono')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
r, theta = np.meshgrid(np.linspace(0, b), np.linspace(0, 2*np.pi))
ax.plot_surface(a*r*np.cos(theta), a*r*np.sin(theta), r, alpha=0.5, cmap='Blues')
plt.show()

Para calcular el momento de inercia del cono con respecto al eje \(OZ\), en coordenadas cilíndricas, habría que resolver la integral:

\[I_z=\iiint_R r^2\delta dV=\iiint_R r^2\delta\; r\,dr\,d\theta\,dz\]

Debe tenerse en cuenta que al hacerse un cambio a coordenadas cilíndricas, en la integral anterior se ha tenido que introducir un factor multiplicativo \(r\) correspondiente al jacobiano del cambio.

En relación a los límites de integración, si se observa que fijado un valor de \(z\) la sección transversal del cono corresponde con un círculo de radio \(z/a\), la integral a calcular sería:

\[I_z=\int_0^b\int_0^{2\pi}\int_0^{z/a}\delta r^3\,dr\,d\theta\,dz = \frac{\delta\pi b^5}{10a^4}\]

r,theta,z,delta,a,b = sp.symbols('r,theta,z,delta,a,b')
sp.integrate(delta*r**3, (r,0,z/a), (theta,0,2*sp.pi), (z,0,b))

\[\displaystyle \frac{\pi b^{5} \delta}{10 a^{4}}\]

Ejercicios propuestos

• Calcular el volumen del sólido delimitado por el cono \(x^2+y^2=z^2\) y la semiesfera \(x^2+y^2+z^2=16\), con \(z\geq 0\).

• A través de una esfera de radio 2, se perfora un agujero cilíndrico de diámetro 1. Suponiendo que el eje del cilindro pase por el centro de la esfera, hallar el volumen del sólido resultante.

• Calcular la masa del sólido tridimensional que se encuentra entre los planos cartesianos y el plano \(x+y+z=10\), asumiendo una densidad constante \(\delta=3\).

• Calcular la masa del sólido comprendido entre las esferas de radio 1 y 5 centradas en el origen cuya densidad en cada punto es inversamente proporcional a la distancia del punto al origen.

• Hallar el volumen, centro de masas y el momento de inercia respecto del eje \(OX\) del sólido limitado por el paraboloide \(2x=y^2+z^2\) y el plano \(x=2\) suponiendo que la densidad en cada punto es proporcional a la distancia al eje \(OX\).