Integración triple

Tras analizar los diferentes conceptos de integración relacionados con las funciones de dos variables, en estas próximas secciones se da el salto al espacio tridimensional para aprender a calcular integrales triples en el espacio, saber utilizar las coordenadas cilíndricas y esféricas, y calcular integrales de superficie y curvilíneas en el espacio. Los conceptos que se estudiarán en esta parte del tema son similares a los analizados en la parte previa, aunque la ampliación en una dimensión más ofrece algunos matices interesantes.

Definición y propiedades

A la hora de considerar el caso de integración triple, es decir la integración de funciones \(f:D\subseteq R^3\rightarrow R\), el primer aspecto importante es que la región de integración será un conjunto \(\Omega\) incluido en el dominio de la función, y por tanto será un sólido tridimensional. En este caso se asumirá que las regiones de integración \(\Omega\) son conjuntos cerrados y acotados en \(R^3\).

Los pasos que conducen a la definición de la integral triple son similares a los realizados para la integración doble:

• Se realiza una subdivisión de la región \(\Omega\) en subregiones totalmente contenidas en \(\Omega\) a partir de una red tridimensional de planos. Cada una de las subregiones tendrá un volumen \(\Delta V_i\).

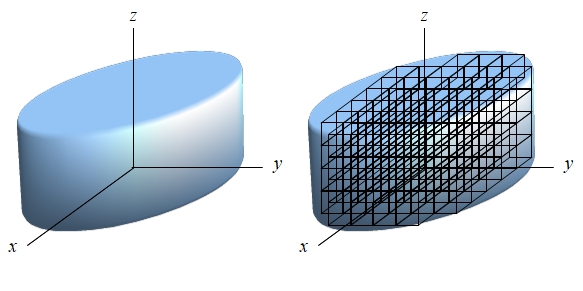
• Se selecciona un punto arbitrario \((x_i,y_i,z_i)\) en cada subregión y se calcula la suma

  \[\sum_{i=1}^n f(x_i,y_i,z_i)\Delta V_i\]

• Se realizan subdivisiones más finas de modo que los volúmenes \(\Delta V_i\) tiendan a 0, obteniendo, en caso de existencia de ese límite, el valor de la integral triple como

\[\iiint_\Omega f(x,y,z)dV=\lim_{\Delta V\rightarrow 0}\sum_{i=1}^n f(x_i,y_i,z_i)\Delta V_i\]

Cuando el límite anterior existe y es finito se dice que la función \(f(x,y,z)\) es integrable sobre \(\Omega\).

Por supuesto, no siempre esos límites existen, de manera que interesa saber qué tipo de condiciones se deberían exigir a la función para garantizar su integrabilidad. Una condición suficiente de integrabilidad es que la función sea continua sobre la región de integración \(\Omega\).

El elemento \(dV\) que aparece en la definición de la integral triple es un elemento diferencial de volumen, que en el caso de trabajar con coordenadas cartesianas se podría representar en la forma \(dV=dx\,dy\,dz\). Este elemento diferencial se obtiene al considerar subregiones en las que \(\Delta V\) tienda a 0. Teniendo en cuenta esto, la integral triple puede denotarse también en la forma:

\[\iiint_\Omega f(x,y,z)dV=\iiint_\Omega f(x,y,z)dx\,dy\,dz\]

Las propiedades básicas de las integrales triples son una mera traslación de lo que se verifica también en las integrales dobles, es decir:

• Si \(f(x,y,z)\) y \(g(x,y,z)\) son dos funciones integrables sobre \(\Omega\subseteq R^3\) y \(a,b\in R\) entonces

\[\iiint\limits_\Omega (a\,f(x,y,z)+b\,g(x,y,z))dV=a\iiint\limits_\Omega f(x,y,z)dV+b\iiint_{\Omega }g(x,y,z)dV\]

• Si \(f(x,y,z)\) es integrable sobre una región \(\Omega \) que puede descomponerse como unión de dos regiones \(\Omega_1\) y \(\Omega_2\) con ningún punto interior común, entonces

\[\iiint\limits_\Omega f(x,y,z)dV=\iiint\limits_{\Omega_1}f(x,y,z)dV+\iiint\limits_{\Omega_2}f(x,y,z)dV\]

• Si \(f(x,y,z)\) es integrable sobre \(\Omega\), también lo es \(|f(x,y,z)|\), verificándose además

\[\left|\iiint\limits_\Omega f(x,y,z)dV\right|\leq\iiint\limits_{\Omega}|f(x,y,z)|dV\]

Cálculo de integrales triples

Al igual que una integral doble se calcula mediante dos integrales iteradas, el cálculo de una integral triple puede reducirse al cálculo de tres integrales iteradas; para ello debe procederse de la siguiente manera:

• Elegir un orden de integración de las variables. Una elección equivocada de dicho orden puede conducir a una integral difícil de calcular. Debe tenerse en cuenta que hay \(3!=6\) posibles órdenes de integración.

• Para cada variable identificar los límites de integración, pudiéndose dar el caso de que los límites de integración de una variable dependan de los valores fijados para las otras variables.

• Realizar las tres integrales iteradas en el orden elegido.

Por supuesto, la dificultad en el cálculo de una integral puede venir por la naturaleza de la propia función a integrar o por la dificultad para caracterizar adecuadamente la región de integración. Para comenzar, se analiza a continuación el caso más sencillo, cuando la región de integración es un paralelepípedo, o una caja rectangular. En este caso los límites de integración de cada variable son independientes de los valores de las otras variables.

---

Ejemplo:

Se considera la integral

\[\iiint\limits_R (xy+z)dV\]

siendo \(R=[0,2]\times[2,5]\times[1,3]\). En este caso el recinto de integración es un sólido tridimensional que resulta sencillo de parametrizar.

import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection
vertices = [[0, 0, 1], [2, 0, 1], [2, 5, 1], [0, 5, 1],
            [0, 0, 3], [2, 0, 3], [2, 5, 3], [0, 5, 3]
]
# Definición de las caras del paralelepípedo
caras = [
    [vertices[0], vertices[1], vertices[2], vertices[3]],
    [vertices[4], vertices[5], vertices[6], vertices[7]],
    [vertices[0], vertices[1], vertices[5], vertices[4]],
    [vertices[2], vertices[3], vertices[7], vertices[6]],
    [vertices[1], vertices[2], vertices[6], vertices[5]],
    [vertices[0], vertices[3], vertices[7], vertices[4]]
]
paralelepipedo = Poly3DCollection(caras, facecolors='cyan', linewidths=1, edgecolors='r', alpha=0.6)
fig, ax = plt.subplots(figsize=(6,6),subplot_kw={"projection": "3d"})
ax.add_collection3d(paralelepipedo)
ax.set_xlim([0, 5]); ax.set_xlabel('Eje X')
ax.set_ylim([0, 5]); ax.set_ylabel('Eje Y')
ax.set_zlim([0, 5]); ax.set_zlabel('Eje Z')
plt.show()

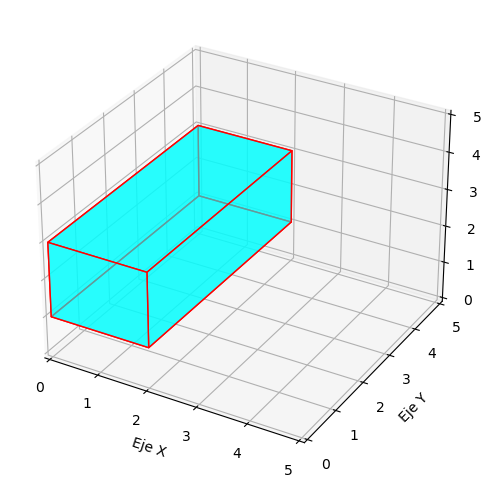
En este caso, al no depender los límites de integración de ninguna variable de las restantes, cualquiera de los 6 órdenes de integración posibles es igualmente válido y de igual complejidad para calcular la integral. Por ejemplo, si se opta por integrar primero en la variable \(x\), luego en la \(y\), y finalmente en la \(z\), la integral resulta:

\[I=\int_1^3\int_2^5\int_0^2 (xy+z)dx\,dy\,dz\]

Se comenzaría calculando la integral interior:

\[\int_0^2 (xy+z)dx = \left.\frac{x^2}{2}y+zx\right|_{x=0}^{x=2}=2y+2z\]

La segunda integral iterada sería entonces:

\[\int_2^5 (2y+2z)dy= \left.y^2+2yz\right|_{y=2}^{y=5}=(25+10z)-(4+4z)=21+6z\]

Y finalmente la integral resultaría

\[I=\int_1^3 (21+6z)dz=\left.21z+3z^2\right|_{z=1}^{z=3}=66\]

Cualquiera de los otros órdenes de integración de las variables conduciría al mismo resultado. Por ejemplo, si se empieza integrando en \(z\), luego en \(y\), finalizando con la integración en \(x\), el resultado sería:

\[I=\int_0^2\int_2^5\int_1^3 (xy+z)dz\,dy\,dx\]

Calculando las integrales iteradas se obtiene:

\[I=\int_0^2\int_2^5(2xy+4)dy\,dx =\int_0^2(21x+12)dx=66\]

En Python la instrucción integrate de SymPy también puede ser utilizada para calcular estas integrales triples:

import sympy as sp
x,y,z = sp.symbols('x,y,z')
sp.integrate(x*y+z, (z,1,3), (y,2,5), (x,0,2))

\[\displaystyle 66\]

---

Por supuesto, no todos los recintos de integración son tan simples. En general, para poder calcular la integral triple sobre un recinto \(R\) se requiere definir el recinto mediante condiciones de la forma

\[ a \leq x \leq b \]

\[ h_1(x) \leq y \leq h_2(x) \]

\[ g_1(x,y) \leq z \leq g_2(x,y) \]

o bien en una forma similar cambiando el orden de las variables. Lo importante es llegar a parametrizar la región mediante una serie de intervalos que cada vez dependen del valor de una variable menos.

Si \(R\) viene determinada por las restricciones anteriores, entonces la integral triple se calcularía de la siguiente manera:

\[\iiint_Rf(x,y,z)dV=\int_a^b\int_{h_1(x)}^{h_2(x)}\int_{g_1(x,y)}^{g_2(x,y)}f(x,y,z)dz\,dy\,dx\]

---

Ejemplo:

Considérese la región del espacio \(R\) delimitada por la superficie parabólica \(y=x^2\) y los planos \(2y+5z=10\), \(z=0\) e \(y=1\). Dicha región puede visualizarse con las siguientes instrucciones Python

import matplotlib.pyplot as plt
import numpy as np
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.set_title('Recinto de integración')
ax.set_xlabel('x'); ax.set_ylabel('y'); ax.set_zlabel('z')
u, v = np.meshgrid(np.linspace(-1, 1), np.linspace(0, 2))
x1, y1, z1 = u, u**2, v
ax.plot_surface(x1, y1, z1, alpha=0.5, cmap='viridis')
u, v = np.meshgrid(np.linspace(-1, 1), np.linspace(0, 1))
x2, y2, z2 = u, v, (10-2*v)/5
ax.plot_surface(x2, y2, z2, alpha=0.5, cmap='BuPu')
u, v = np.meshgrid(np.linspace(-1, 1), np.linspace(0, 2))
x3, y3, z3 = u, 1, v
ax.plot_surface(x3, y3, z3, alpha=0.5, cmap='PuBu')
plt.show()

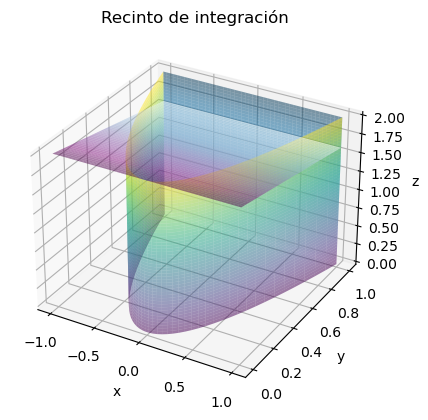
Como puede apreciarse, la altura que pueden alcanzar los puntos de \(R\), es decir el valor de la variable \(z\) en \(R\), depende del punto \((x,y)\) que se considere en el plano OXY. Realmente, al poder variar libremente el valor de la variable \(x\) en el plano que cierra el sólido por la parte superior, el valor de la \(z\) únicamente depende de la coordenada \(y\).

En definitiva, fijado \((x,y)\) el valor de la variable \(z\) varía entre:

\[0\leq z\leq \frac{10-2y}{5}\]

Para determinar los intervalos de variación de las restantes variables, debe analizarse la forma que tiene la proyección del sólido \(R\) sobre el plano \(OXY\), dicha proyección permite ver cómo el intervalo de variación de la variable \(y\) depende del valor que se fije para la \(x\). En concreto, dado un valor \(x\) en el intervalo

\[-1\leq x\leq 1\]

la variable \(y\) varía entre

\[x^2\leq y \leq 1\]

import sympy as sp
x,y = sp.symbols('x,y')
sp.plot_implicit(sp.And(y>=x**2, y<=1, x>=-1, x<=1), (x, -1, 1), (y, 0, 1));

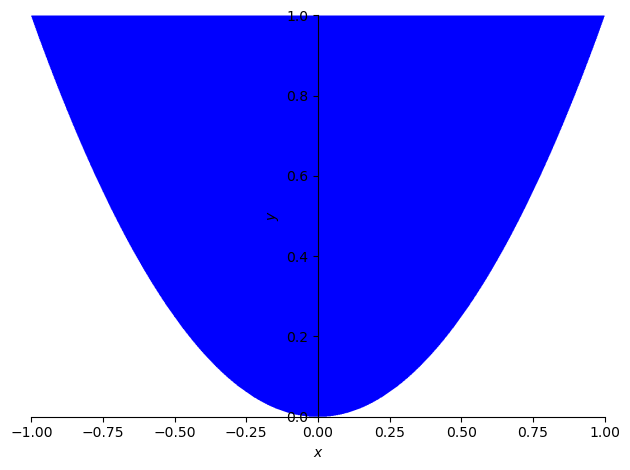
A la vista de estas condiciones que determinan la región \(R\), lo recomendable para calcular una integral sobre \(R\) es realizar en primer lugar la integral iterada sobre la variable \(z\), después sobre la \(y\), para terminar integrando en \(x\). Por ejemplo, a continuación se calcula el valor de la integral

\[I=\iiint_R (x+y+z)dV\]

Esta integral podría calcularse mediante 3 integrales iteradas:

\[I=\int_{-1}^{1}\int_{x^2}^{1}\int_{0}^{\frac{10-2y}{5}}(x+y+z)dz\,dy\,dx\]

Tras realizar la integral interior, se obtiene

\[I = \int_{-1}^{1}\int_{x^2}^{1} \left( (x+y)\frac{10-2y}{5}+\frac{(10-2y)^2}{50}\right)dy\,dx\]

\[= \int_{-1}^{1}\int_{x^2}^{1} \left(2+2x+\frac{6y}{5}-\frac{2xy}{5}-\frac{8y^2}{25}\right)dy\,dx\]

Tras realizar la segunda integral iterada se llega a

\[I=\int_{-1}^{1}\left( \frac{187}{75} + \frac{9\,x}{5} - 2\,x^2 - 2\,x^3 - \frac{3\,x^4}{5} + \frac{x^5}{5} + \frac{8\,x^6}{75}\right)dx\]

Y finalmente

\[I=\frac{1808}{525}\approx 3.44\]

Esta integral triple puede calcularse fácilmente con la función de integración simbólica del paquete SymPy:

import sympy as sp
x,y,z = sp.symbols('x,y,z')
sp.integrate(x+y+z, (z,0,(10-2*y)/5), (y,x**2,1), (x,-1,1))

\[\displaystyle \frac{1808}{525}\]

sp.integrate(x+y+z, (z,0,(10-2*y)/5), (y,x**2,1), (x,-1,1)).evalf()

\[\displaystyle 3.44380952380952\]

Cálculo de integrales triples de manera numérica con Python

De nuevo, debe tenerse en cuenta que determinadas integrales triples no pueden calcularse de manera simbólica y se necesita recurrir a un procedimiento numérico de aproximación de su valor.

En el caso de integrales triples, la integración numérica puede hacerse con la función tplquad(F, a, b, g, h, q, r) del paquete SciPy de Python. Esta función se aplica a integrales que puedan definirse de la siguiente forma:

\[I=\int_a^b\left(\int_{g(x)}^{h(x)}\left(\int_{q(x,y)}^{r(x,y)} F(z,y,x)dz\right)dy\right)dx\]

De nuevo debe tenerse en cuenta el orden inusual de las variables \(z,y,x\) en la definición de la función, por lo que también se podría realizar un cambio de nombre de las variables y obtener una integral equivalente:

\[I=\int_a^b\left(\int_{g(z)}^{h(z)}\left(\int_{q(z,y)}^{r(z,y)} f(x,y,z)dx\right)dy\right)dz\]

con \(f(x,y,z)=F(z,y,x)\).

En cualquiera de los casos que se considere, es importante observar y respetar el orden de las variables en la definición de la función a integrar y las funciones que determinan los límites de integración de las variables, respetando en todo momento el orden que aparece en las fórmulas anteriores.

La integral del ejercicio anterior se podría también calcular con la instrucción: integrate.tplquad(f, a, b, g, h, q, r), sin embargo para su cálculo numérico hay que tener en cuenta que estaría expresada en la forma:

\[I=\int_{-1}^{1}\int_{x^2}^{1}\int_{0}^{\frac{10-2y}{5}}(x+y+z)dz\,dy\,dx = \int_a^b\left(\int_{g(x)}^{h(x)}\left(\int_{q(x,y)}^{r(x,y)} F(z,y,x)dz\right)dy\right)dx\]

considerando como función a integrar \(F(z,y,x)=x+y+z\), \(a=-1\), \(b=1\), \(g(x)=x^2\), \(h(x)=1\), \(q(x,y)=0\) y \(r(x,y)=(10-2y)/5\). La única precaución que hay que tener a la hora de definir las variables es el orden en el que aparecen.

from scipy import integrate
f = lambda z,y,x: x+y+z
a, b = -1, 1
g, h = lambda x: x**2, lambda x: 1
q, r = lambda x,y: 0, lambda x,y: (10-2*y)/5
integrate.tplquad(f, a, b, g, h, q, r)

(3.443809523809524, 4.9660813427627864e-14)

La integral anterior puede ser calculada en los dos modos, simbólico y numérico, sin embargo existen integrales que no admiten una integración simbólica y la única alternativa sería la de recurrir a una aproximación numérica de su resultado. A continuación se muestra un ejemplo.

---

Ejemplo:

Se plantea el cálculo de la integral

\[\iiint_V\left(\frac{\cos z}{e^{x^2+y^2}}\right)dV\]

donde \(V\) viene delimitado por las condiciones

\[0\leq x\leq 2,\;\;\; 1\leq y\leq 2,\;\;\; x-y\leq z\leq x+y\]

Se puede comprabar que el intento de resolución simbólica no permite obtener ningún resultado. Tras unos segundos intentando su resolución Python termina por dejar la integral sin resolver completamente:

x,y,z = sp.symbols('x,y,z')
F = sp.cos(z)/sp.exp(x**2+y**2)
sp.integrate(F, (z,x-y,x+y), (y,1,2), (x,0,2))

\[\displaystyle \int\limits_{0}^{2} \left(\int\limits_{1}^{2} \left(- e^{- y^{2}} \sin{\left(x - y \right)}\right)\, dy + \int\limits_{1}^{2} e^{- y^{2}} \sin{\left(x + y \right)}\, dy\right) e^{- x^{2}}\, dx\]

En este caso no queda más remedio que recurrir a la integración numérica. Teniendo en cuenta que la integración se expresa de la siguiente manera

\[I=\int_{0}^{2}\int_{1}^{2}\int_{x-y}^{x+y}\left(\frac{\cos z}{e^{x^2+y^2}}\right)dz\,dy\,dx = \int_a^b\left(\int_{g(x)}^{h(x)}\left(\int_{q(x,y)}^{r(x,y)} F(z,y,x)dz\right)dy\right)dx\]

a la hora de definir la expresión lambda habría que indicar el orden de las variables en el orden \(z,y,x\):

F = lambda z,y,x: np.cos(z)/np.exp(x**2+y**2)
a, b = 0, 2
g, h = 1, 2
q, r = lambda x,y: x-y, lambda x,y: x+y
integrate.tplquad(F, a, b, g, h, q, r)

(0.1751836791478516, 6.8531234638332856e-15)

Ejercicios propuestos

• Calcular la integral de la función \(f(x,y,z)=x + 2y + z\) sobre el tetraedro de vértices \((0,0,0)\), \((1,0,0)\), \((0,2,0)\), y \((0,0,1)\).

• Calcular la siguiente integral triple \(\iiint_R xyz\,dV\) siendo \(R\) el tetraedro delimitado por los planos cartesianos y el plano de ecuación \(x+\frac{y}{2}+\frac{z}{3}=1\).

• Calcular \(\iiint\limits_{R} dV\) siendo \(R\) la región tridimensional comprendida entre los planos cartesianos y el plano \(x+y+z=10\).

• Calcular la siguiente integral \(\iiint\limits_{R} xy^2z^2dV\) siendo \(R\) la región que viene delimitada por la superficie \(z=xy\) y los planos \(y=x\), \(x=1\), \(z=0\).

• Dada la región \(R\) delimitada por \(z=0\), \(z=y/2\), \(x=0\), \(x=1\), \(y=0\), \(y=2\), calcular la integral

\[\iiint\limits_{R} (x+y-z)dV\]