Integrales de superficie de campos escalares

A la hora de trabajar con campos tridimensionales surge la posibilidad de estudiar un nuevo concepto: la integral de superficie. En esta sección se analizarán este concepto y se presentarán algunas aplicaciones prácticas. En cierto modo la integral de superficie generaliza el concepto de integral de línea para considerar la integral del campo sobre toda una superficie.

Integral de superficie de un campo escalar:

Dado un conjunto conexo \(\Omega\subseteq R^2\) y una superficie parametrizada \(S\) definida por

\[\begin{split}\begin{array}{rl} \vec{s}:\Omega &\longrightarrow R^3\\ (u,v) &\longrightarrow \vec{s}(u,v)=(s_1(u,v),s_2(u,v),s_3(u,v)) \end{array}\end{split}\]

Si \(F(x,y,z)\) es un campo escalar definido sobre la superficie \(S\), se define la integral de superficie de \(F\) sobre \(S\) como:

\[\iint_S F(x,y,z)ds = \iint_\Omega F(\vec{s}(u,v)) \left\| \frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v) \right\| du\,dv\]

Se podría demostrar que la definición anterior no depende de la parametrización elegida para la superficie. Además, obviamente el valor de la integral solo depende del valor del campo sobre los puntos de la superficie.

Se cumplirían igualmente una serie de propiedades básicas similares a las integrales de linea:

• Linealidad:

\[\iint_S (\lambda F_1(x,y,z)+\mu F_2(x,y,z))ds=\lambda \iint_S F_1(x,y,z)ds +\mu \iint_S F_2(x,y,z)ds\]

• Aditividad en la superficie de integración:

\[\iint_{S_1+S_2} F(x,y,z)ds=\iint_{S_1} F(x,y,z)ds+\iint_{S_2} F(x,y,z)ds\]

• Acotación: si existe \(M\in R\) tal que \(|F(x,y,z)|\leq M\) para todo punto de la superficie, entonces

\[\left|\iint_{S} F(x,y,z)ds\right|\leq M\,Area(S)\]

Al igual que la longitud de una curva puede calcularse mediante una integral, el área de una superficie también puede calcularse mediante una integral de superficie. En concreto, dada la superficie \(S\) con parametrización \(\vec{s}(u,v)\) con \((u,v)\in\Omega\), de clase \(C^1\) e inyectiva en \(\Omega\), salvo quizás en un conjunto de medida nula, el área de la superficie es:

\[Area(S)=\iint_S ds = \iint_\Omega \left\| \frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v) \right\| du\,dv\]

Para entender la razón por la que esa integral de superficie permite calcular el área de la superficie, conviene recordar que los vectores \(\frac{\partial \vec{s}}{\partial u}(u,v)\) y \(\frac{\partial \vec{s}}{\partial v}(u,v)\) determinan el plano tangente a la superficie. Además, el área de un paralelogramo determinado por un punto \((x_0,y_0,z_0)\) y dos vectores \(\vec{a}\) y \(\vec{b}\) es precisamente \(\|\vec{a}\times\vec{b}\|\).

---

Ejemplo:

Se calcula a continuación el área de la superficie del cono \(z^2=x^2+y^2\) comprendida entre los planos \(z=0\) y \(z=5\).

Para comenzar se cargarán los paquetes necesarios para la integración simbólica, y se definirá un sistema de coordenadas y dos parámetros simbólicos para las parametrizaciones de las superficies.

import sympy as sp
import sympy.vector as vec
S = vec.CoordSys3D('')
u,v = sp.symbols("u,v")

La parametrización del cono sería:

x, y, z= v*sp.cos(u), v*sp.sin(u), v

El siguiente paso es construir los dos vectores que determinan el plano tangente en cada punto de la superficie, y a partir de ellos el vector normal como producto vectorial de ambos:

v1 = sp.diff(x,u)*S.i + sp.diff(y,u)*S.j + sp.diff(z,u)*S.k
v2 = sp.diff(x,v)*S.i + sp.diff(y,v)*S.j + sp.diff(z,v)*S.k
normal = v1.cross(v2)
sp.simplify(normal)

\[\displaystyle (v \cos{\left(u \right)})\mathbf{\hat{i}_{}} + (v \sin{\left(u \right)})\mathbf{\hat{j}_{}} + (- v)\mathbf{\hat{k}_{}}\]

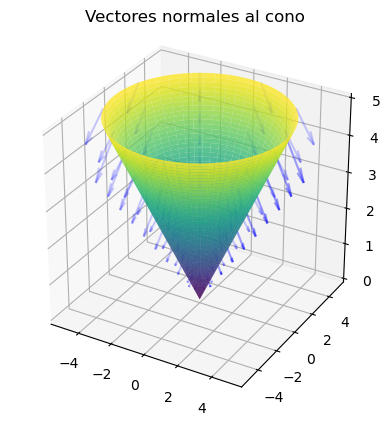
Se puede hacer una representación de la superficie junto con los vectores normales para comprobar la orientación que definen sobre la propia superficie.

import matplotlib.pyplot as plt
import numpy as np

# Superficie
u, v = np.meshgrid(np.linspace(0,2*np.pi), np.linspace(0,5))
x, y, z = v*np.cos(u), v*np.sin(u), v
# Vectores normales
uu, vv = np.meshgrid(np.linspace(0,2*np.pi,10), np.linspace(0,5,10))
xx, yy, zz = vv*np.cos(uu), vv*np.sin(uu), vv
cx, cy, cz = vv*np.cos(uu), vv*np.sin(uu), -vv
# Gráfica la superficie y los vectores normales
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Vectores normales al cono')
ax.plot_surface(x, y, z, cmap='viridis', alpha=0.8)
ax.quiver(xx, yy, zz, cx, cy, cz, color='blue', alpha=0.2, length=0.2)
ax.set_box_aspect([1, 1, 1])
plt.show()

Para calcular el área de esa superficie habrá que calcular la integral del módulo del vector normal:

u,v = sp.symbols("u,v")
area = sp.integrate(normal.magnitude(), (u,0,2*sp.pi), (v,0,5))
print('Area:',area)
area.evalf()

Area: 25*sqrt(2)*pi

\[\displaystyle 111.072073453959\]

Una alternativa más rápida es utilizar la función vector_integrate() del módulo Vector. Esta función ya fue utilizada anteriormente para el cálculo de integrales de línea, pero también puede usarse para integrales de superficie. La propia función es capaz de identificar si la entidad geométrica que se le pasa como segundo argumento es una curva o una superficie, realizando la integral según corresponda. Siguiendo con el ejemplo del cono, la misma integral anterior podría ser calculada de la siguiente manera:

superficie = vec.ParametricRegion((v*sp.cos(u), v*sp.sin(u), v), (u,0,2*sp.pi), (v,0,5))
F = 1
vec.vector_integrate(F, superficie)

\[\displaystyle 25 \sqrt{2} \pi\]

---

En el caso particular en el que la superficie \(S\) esté definida de forma explícita \(z=h(x,y)\) con \((x,y)\in\Omega\), la parametrización de la superficie sería:

\[x=x;\;\;y=y;\;\;z=h(x,y)\;\;\mbox{ con }(x,y)\in\Omega\]

y operando se obtendría

\[\frac{\partial \vec{s}}{\partial x}(x,y)\times \frac{\partial \vec{s}}{\partial y}(x,y)= \left(-\frac{\partial h}{\partial x}(x,y),-\frac{\partial h}{\partial y}(x,y),1\right)\]

Por tanto, el área de la superficie podría calcularse directamente con la integral siguiente.

Área de superficie explícita:

El área de la superficie \(z=h(x,y)\) con \((x,y)\in\Omega\) sería

\[Area(S)=\iint_\Omega \sqrt{1+\left(\frac{\partial h}{\partial x}(x,y)\right)^2 +\left(\frac{\partial h}{\partial y}(x,y)\right)^2}dx\,dy\]

De igual manera, la integral de superficie del campo \(F(x,y,z)\) sobre la superficie definida en forma explícita \(z=h(x,y)\) con \((x,y)\in\Omega\), sería:

\[ \iint_S F(x,y,z)ds =\iint_\Omega F(x,y,h(x,y)) \sqrt{1+\left(\frac{\partial h}{\partial x}(x,y)\right)^2 +\left(\frac{\partial h}{\partial y}(x,y)\right)^2}dx\,dy \]

---

Ejemplo:

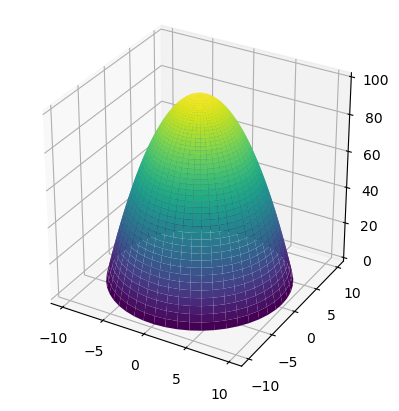
El área del paraboloide \(z=100-x^2-y^2\) con \(z\geq 0\), podría calcularse con una integral de superficie. El dominio \(\Omega\) sería en este caso la proyección de la superficie sobre el plano OXY, es decir el círculo dado por \(x^2+y^2\leq 100\).

u, v = np.meshgrid(np.linspace(0,10), np.linspace(0,2*np.pi))
x, y = u*np.cos(v), u*np.sin(v)
z = 100-x**2-y**2
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.plot_surface(x, y, z, cmap='viridis')
ax.set_box_aspect([1, 1, 1])
plt.show()

Al estar definida de forma explícita la superficie, su área se calcularía con la integral doble sobre \(\Omega\) de la siguiente función:

x,y = sp.symbols('x,y')
h = 100 - x**2 - y**2
sp.sqrt(1 + sp.diff(h,x)**2 + sp.diff(h,y)**2)

\[\displaystyle \sqrt{4 x^{2} + 4 y^{2} + 1}\]

Para calcular la integral se podría hacer un cambio de variables a coordenadas polares

r, alpha = sp.symbols('r,alpha')
x, y = r*sp.cos(alpha), r*sp.sin(alpha)
F = sp.sqrt(4*x**2+4*y**2+1)
Jacobiano = r
sp.integrate(F*Jacobiano, (alpha, 0, 2*sp.pi), (r, 0, 10))

\[\displaystyle - \frac{\pi}{6} + \frac{401 \sqrt{401} \pi}{6}\]

Una alternativa más directa para el cálculo con Python es usar la función de integración vectorial.

superficie = vec.ParametricRegion((r*sp.cos(alpha), r*sp.sin(alpha), 100-r**2), (alpha,0,2*sp.pi), (r,0,10))
vec.vector_integrate(1, superficie)

\[\displaystyle - \frac{\pi}{6} + \frac{401 \sqrt{401} \pi}{6}\]

---

Además del cálculo del área de una superficie, las integrales de superficie tienen otras aplicaciones prácticas:

• Cálculo de la masa: si una superficie \(S\) tiene densidad superficial \(\rho(x,y,z)\), entonces su masa es

\[masa(S)=\iint_S \rho(x,y,z)ds\]

• Centro de masas: el centro de masas de la superficie \(S\) vendría dado por:

\[\bar{x}=\frac{\iint_S x\rho(x,y,z)ds}{masa(S)};\;\;\; \bar{y}=\frac{\iint_S y\rho(x,y,z)ds}{masa(S)};\;\;\; \bar{z}=\frac{\iint_S z\rho(x,y,z)ds}{masa(S)}\]

---

Ejemplo:

Considérese la superficie del triángulo \(T\) de vértices \((1,0,0)\), \((0,1,0)\) y \((0,0,1)\), siendo la densidad superficial \(\delta(x,y,z)=xyz\). Para calcular su masa en primer lugar se necesita una parametrización de la superficie. La superficie está contenida en el plano \(x+y+z=1\), y una parametrización de la curva sería:

\[x=u;\;\;y=v;\;\;z=1-u-v\;\;\mbox{ con }(u,v)\in\Omega\]

siendo \(\Omega\) el triángulo en el plano \(OXY\) de vértices \((0,0)\), \((1,0)\) y \((0,1)\)

Por tanto, la masa del triángulo sería:

\[Masa(T)=\iint_T xyz\, ds = \iint_\Omega uv(1-u-v)\left\| \frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v) \right\| du\,dv\]

En este caso

\[\frac{\partial \vec{s}}{\partial u}(u,v) = (1,0,-1);\;\;\; \frac{\partial \vec{s}}{\partial v}(u,v) = (0,1,-1)\]

y por tanto

\[\frac{\partial \vec{s}}{\partial u}(u,v)\times \frac{\partial \vec{s}}{\partial v}(u,v) = (1,1,1)\]

En definitiva

\[Masa(T) = \iint_\Omega uv(1-u-v)\sqrt{3} du\,dv \]

\[ = \sqrt{3}\int_0^1\left(\int_0^{1-u} (uv-u^2v-uv^2)dv\right)du = \frac{\sqrt{3}}{120}\]

---

La integral de superficie puede ser utilizada también para calcular, por ejemplo, la carga total de una superficie conociendo la densidad de carga \(\rho(x,y,z)\) en sus puntos. En ese caso, la carga total sería

\[Carga=\iint_S\rho(x,y,z)ds\]

---

Ejemplo:

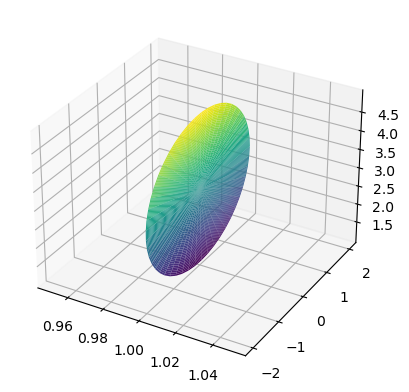
Se tiene una superficie circular de radio 2 y situada en posición vertical sobre el plano \(x=1\) y centrada en el punto \((1,0,3)\), asumiendo que la densidad superficial de carga es \(\rho(x,y,z)=xy+z\), se desea calcular la carga total.

En primer lugar se debe parametrizar la superficie, en este caso podemos comprobar además que la parametrización es correcta realizando una representación gráfica de la misma.

u, v = np.meshgrid(np.linspace(0, 2, 50), np.linspace(0, 2*np.pi, 50))
x, y, z = 1, u*np.cos(v), 3 + u*np.sin(v)
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.plot_surface(x, y, z, cmap='viridis')
plt.show()

La integral de superficie se calcularía de la siguiente manera:

u, v = sp.symbols('u,v')
disco = vec.ParametricRegion((1, u*sp.cos(v), 3+u*sp.sin(v)), (u,0,2), (v,0,2*sp.pi))
rho = S.x * S.y + S.z
vec.vector_integrate(rho, disco)

\[\displaystyle 12 \pi\]

Ejercicios propuestos

• Calcular la integral de superficie \(\iint_S y\,ds\) siendo \(S\) la superficie definida por la ecuación \(z=x+y^2\) con \(0\leq x\leq 1\), \(0\leq y\leq 2\).

• Calcular la integral de superficie \(\iint_S x^2y^2z^2\,ds\) siendo \(S\) la superficie esférica \(x^2+y^2+z^2=a^2\).

• Calcular el área de la parte del paraboloide \(z=x^2+y^2\) que se encuentra por debajo del plano \(z=9\).

• Una superficie metálica tiene forma de semiesfera de radio \(R\) y su densidad superficial viene dada por \(\rho(x,y,z)=x^2+y^2\). Calcular la masa de la superficie.

• Calcular las coordenadas del centro de masas de una lámina helicoidal que está descrita por la parametrización \(\vec{s}(r,\theta)=(r\cos\theta,r\sin\theta,\theta)\) con \(0\leq r\leq 2\sqrt{2}\) y \(0\leq\theta\leq 2\pi\), y cuya densidad superficial en un punto \((x,y,z)\) es

\[\rho(x,y,z)=\sqrt{x^2+y^2+1}\]