Introducción al cálculo diferencial avanzado para la ingeniería#

La modelización matemática en la ingeniería#

La matemática desempeña un papel fundamental en la ingeniería, hasta el punto que no sería una exageración asegurar que la ingeniería moderna no existiría sin las matemáticas.

Dentro de la actividad científica siempre han tenido una papel destacado las matemáticas como ciencia basada en la abstracción y el razonamiento deductivo. En las diferentes ramas de la ingeniería las matemáticas se han convertido en parte integral, facilitando la creación de nuevos métodos de solución de problemas de tipo ingenieril.

Algunos de los rasgos característicos que diferencian las matemáticas del resto de ciencias son:

  • Gran nivel de abstracción: el concepto matemático es el resultado de la abstracción de todas las propiedades de un objeto.

  • El uso de un simbolismo propio.

  • Rigor lógico: rechazo de toda incoherencia lógica

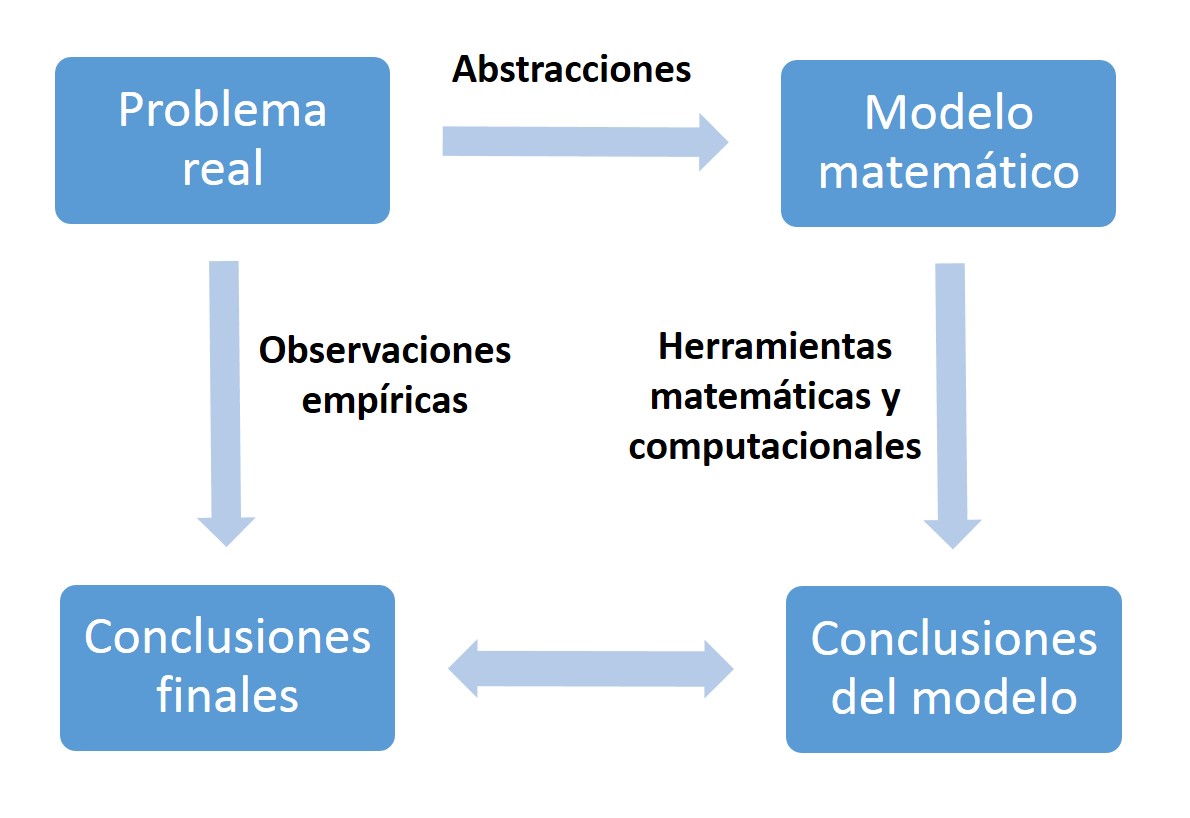
En la ingeniería es frecuente el uso de la modelización, lo que requiere en muchas ocasiones la creación de nuevas estructuras matemáticas y el desarrollo de métodos de resolución específicos. La modelización matemática es el elemento básico en la aplicación de las matemáticas en ingeniería, y consiste básicamente en el paso de un problema real a uno conceptual. Este proceso comienza por un análisis del fenómeno real y la realización de hipótesis simplificadoras que permitan, mediante las correspondientes abstracciones, su descripción matemática (modelo). Es importante puntualizar, que todo modelo matemático es una abstración de la realidad, y por muy complejo que sea siempre supone un cierto grado de simplificación.

Una vez que se dispone de un modelo matemático entran en juego las técnicas matemáticas que permiten su análisis. La complejidad de los modelos que surgen en situaciones reales hace que hoy en día resulte esencial disponer de las herramientas computacionales adecuadas para su análisis, de manera que las matemáticas y la computación actúan de manera coordinada.

Las conclusiones obtenidas tras el análisis del modelo deben ser contrastadas con resultados experimentales, fase conocida como validación del modelo. Esta validación puede llevar consigo la necesidad de realizar modificaciones o ajustes en el modelo inicial.

Para un ingeniero la utilización de modelos matemáticos resulta necesaria por varios motivos:

  • Construir un modelo matemático puede servir para descubrir nuevas propiedades o relaciones que pueden pasar desapercibidas en la observación directa del fenómeno o problema a analizar.

  • Plantearse la construcción de un modelo matemático obliga a conocer mejor el problema, a identificar las variables que intervienen y los efectos de unas sobre otras.

  • El disponer de un modelo permite su análisis con técnicas matemáticas y computacionales de mayor o menor grado de sofisticación.

  • En muchas ocasiones la enorme cantidad de datos e información que intervienen en el problema obliga necesariamente a su tratamiento mediante técnicas analíticas de carácter matemático.

  • Permite la experimentación sobre el modelo. En muchas ocasiones la experimentación directa sobre el fenómeno real puede ser desaconsejable o simplemente imposible. Experimentar sobre el modelo es además menos costoso y más rápido. El modelo permite comprobar los efectos de posibles cambios en determinados parámetros sin el riesgo de sufrir los efectos reales de dichos cambios.

Competencias matemáticas e informacionales del profesional de la ingeniería#

En un sentido amplio, la competencia matemática es la habilidad para entender, juzgar y hacer uso de conceptos matemáticos en contextos y situaciones relevantes. El desarrollo de esta competencia es el objetivo principal de este curso de cálculo diferencial avanzado para la ingeniería. Esta competencia general se desagrega en 8 competencias más específicas que se tratarán de desarrollar en los participantes del curso:

  1. Pensar matemáticamente: conocimiento del tipo de cuestiones que pueden ser tratadas con las matemáticas y el tipo de respuestas que las matemáticas pueden o no pueden dar a esas cuestiones.

  2. Razonar matemáticamente: habilidad de entender y evaluar argumentaciones matemáticas existentes.

  3. Plantear y resolver problemas matemáticos: habilidad de identificar y especificar problemas matemáticos, pero también de resolverlos a través del conocimiento de los algoritmos adecuados.

  4. Modelar matemáticamente: competencia con dos componentes, por un lado la habilidad para analizar y trabajar sobre modelos existentes, pero también la capacidad para construir modelos.

  5. Representar entidades matemáticas: entender el uso de todo tipo de representaciones matemáticas (simbólicas, numéricas, gráficas y visuales, verbales,…), conociendo sus ventajas y limitaciones y siendo capaz de elegir la más adecuada en cada contexto.

  6. Manipular símbolos matemáticos y formalismo: entender el lenguaje matemático simbólico y formal y su relación con el lenguaje natural.

  7. Comunicar en, con y sobre matemáticas: entender las afirmaciones matemáticas realizadas por otros y ser capaz de expresar matemáticamente las ideas propias en diferentes maneras.

  8. Hacer uso de herramientas y ayudas: conocimiento de las herramientas, pero también de sus limitaciones. Hacer uso de ellas de manera eficiente.

Precisamente, en relación a esto último, el uso de las herramientas apropiadas, un aspecto esencial en la labor del ingeniero es el uso de herramientas de software que faciliten el proceso de resolución de los modelos planteados. Si importante es el uso del ordenador en cualquier disciplina de carácter científico, lo es especialmente en la matemática aplicada. De hecho, los avances de la informática han estado íntimamente ligados a los avances de muchas áreas de la matemática como la optimización e investigación operativa. Hoy en día además, en la era del big data, la existencia de soluciones tecnológicas capaces de gestionar cantidades masivas de datos debe venir de la mano del desarrollo de metodologías matemáticas para su tratamiento efectivo y la extracción de conocimiento a partir de los datos.

Haciendo un poco de historia, con la aparición de los primeros computadores digitales, las técnicas del cálculo numérico sufrieron un importante impulso. Estos primeros ordenadores estuvieron dedicados principalmente a procesos de simulación, optimización, análisis numérico,… En estos años parecía que la única utilidad que los ordenadores podían aportar a las matemáticas y la ingeniería era la realización de operaciones numéricas con gran cantidad de datos y a gran velocidad. Pero los avances de la microinformática contribuyeron al abaratamiento de los equipos, surgiendo los primeros ordenadores personales. Los ordenadores pudieron llegar así a un público más amplio, aumentando la demanda y creación de nuevos tipos de software. Así se desarrollo una nueva concepción del uso del ordenador para el cálculo matemático: el trabajo en modo simbólico y exacto. Actualmente ambas tendencias de computación, numérica y simbólica, se desarrollan de manera paralela y se intercomplementan, aprovechando las ventajas de cada una.

En definitiva, para el ingeniero del siglo XXI, resulta esencial tener destrezas para la utilización del ordenador en su día a día, manejar distintas herramientas informáticas y lenguajes de programación. Pero también es cierto que la simplicidad de pulsar una tecla no debe encubrir el valor esencial de comprender lo que se hace y valorar lo obtenido por el software utilizado. No debe pensarse que el ordenador lo resuelve todo y entender sus potencialidades, pero también sus limitaciones. La máquina (ordenador) es una herramienta que nos ofrece fortalezas complementarias a la del ser humano (capacidad de almacenamiento de información, velocidad de procesamiento y cálculo,…) pero tampoco nos debemos convertir en máquina-dependientes.

Uso de software en el contexto del curso: el lenguaje Python#

A la hora de plantearse la elección del software adecuado para su utilización como ayuda en la modelización y resolución de problemas de ingeniería, existen diferentes criterios a tener en cuenta. Pero también conviene entender que en cualquier profesión la variedad de herramientas a utilizar es amplia, por lo que también parece lógico que el ingenierio deba conocer las potencialidades y posibilidades de diferentes softwares o lenguajes de programación.

Un primer dilema que se puede plantear es optar por lenguajes de programación con las librerías adecuadas u optar por paquetes especializados. Existen lenguajes de programación utilizados habitualmente para la implementación de software científico como puedan ser Fortran, C o C++, y otros que recientemente están ganando una enorme popularidad como Phyton. Por otro lado, tenemos paquetes especializados, como puedan ser Maxima, SAGE, Octave, Mathematica o Matlab, algunos de los cuáles además incorporan sus propios lenguajes de programación dotándoles de más versatilidad y mayores posibilidades de uso.

El uso de lenguajes de programación requiere de una mayor cualificación y preparación previa, aunque por otro lado suelen ser idóneos si se conocen en profundidad y tienen una mayor aplicabilidad. En cambio, los paquetes especializados requieren menos conocimientos para su utilización, ya que generalmente permiten un uso interactivo (pregunta-respuesta), aunque también es cierto que algunos incorporan su propio lenguaje de programación.

En este caso se ha decidido utilizar el lenguaje de programación Python como herramienta de apoyo para el desarrollo de la asignatura. Los motivos de esta elección son varios:

  1. Se trata de un lenguaje concebido como proyecto “open source” (código abierto), lo que implica la libre disponibilidad del lenguaje y de una enorme variedad de paquetes desarrollados sobre él.

  2. Es un lenguaje de enorme popularidad y aplicabilidad práctica en una amplísima variedad de disciplinas. Dos referencias pueden dar fé de ello:

  3. Es un lenguaje intrepretado, lo que facilita su uso interactivo (entrada-salida)

  4. Resulta un lenguaje con una codificación simple y fácil de aprender.

  5. Es multiplataforma y permite además su utilización en servicios de cloud computing. Esto garantiza la posibilidad de usar un mismo código con independencia de sistemas operativos o incluso dispositivos (ordenadores, smartphones, tablets,…)

  6. Desde el punto de vista de cálculo matemático, dispone de un buen número de paquetes y librerías de funciones ya programadas, tanto para trabajar en modo numérico como simbólico.

  7. Es un lenguaje muy apropiado para trabajar en proyectos de big data y gestionar de manera eficiente datos, tanto estructurados como no estructurados.

Como todo lenguaje de programación, Python permite trabajar con diferentes tipos de datos, no solo numéricos, sino también cadenas de caracteres y estructuras de datos (listas, tuplas, diccionarios y conjuntos). Ofrece además la posibilidad de usar diferentes estructuras de control (iterativas y condicionales) y construir funciones. Python dispone además de una estructura modular en la que además de las funcionalidades básicas se pueden añadir nuevas prestaciones a través de paquetes complementarios. En este caso, en el contexto de esta asignatura se utilizarán varios paquetes:

  • Numpy: paquete básico de operaciones numéricas con datos, permite además construir estructuras de tipo array.

  • SymPy: paquete con rutinas matemáticas de cálculo simbólico

  • Matplotlib: paquete con herramientas para la representación gráfica de datos y funciones

  • SciPy: paquete con implementación de técnicas matemáticas avanzadas

Además, para el desarrollo de las actividades prácticas, los comandos e instrucciones Python se pueden “ejecutar” de diversas maneras:

  • Ejecución de órdenes directas enviándolas al intérprete de comandos

  • Creación de ficheros con extensión .py que son ejecutados por el intérprete

  • Integración de código dentro de cuadernos computacionales (Jupyter Notebooks) que integran elementos multimedia y código ejecutable. Esta será la opción principal que se usará en el desarrollo de actividades prácticas en este curso, e igualmente los notebooks serán el elemento básico para distribuir los materiales docentes. Los cuadernos computacionales son documentos con extensión ipynb.

Además de esas diferentes formas de ejecución de código Python, se podrán utilizar dos formas de trabajo:

  • En una plataforma local instalada en nuestros equipos. La plataforma de trabajo más usada es Anaconda https://www.anaconda.com/, que integra, entre otras herramientas, un completo entorno de desarrollo integrado (Spyder) y herramientas para elaborar los cuadernos computacionales (Jupyter Notebboks y JupyterLab). Por supuesto, Anaconda incorpora también el intérprete Python y una herramienta para trabajo en modo “terminal”.

  • La otra alternativa es recurrir a un servicio de computación en la nube (cloud computing) que permita ejecutar los notebooks sin necesidad de tener una plataforma propia. Existen diversos servicios, pero uno de los más populares es Google Colaboratory (https://colab.research.google.com/)

Trabajo en modo numérico y simbólico con Python#

Para entender la forma de trabajo interactivo (entrada-salida) de Python y la diferencia entre un modo de trabajo simbólico y numérico, se muestran a continuación algunos ejemplos de uso de los paquetes Numpy y SymPy. Aunque ambos paquetes ya vienen instalados en las plataformas habituales (lo están tanto en Anaconda como en Google Colab), su utilización exige una importación previa de los mismos. Lo habitual es además importar los paquetes asignándoles un “alias” que permita su referencia posterior. Eso se puede hacer de la siguiente manera:

import numpy as np
import sympy as sp

Ambos paquetes cuentan con las funciones matemáticas habituales además de algunas de las constantes comúnes en diferentes modelos matemáticos. Por ejemplo, en ambos paquetes se encuentra definido el número \(\pi\), pero podemos observar una clara diferencia en su tratamiento:

np.pi

3.141592653589793

sp.pi
\[\displaystyle \pi\]

El paquete Numpy lo trata de manera numérica y lo que nos devuelve es una aproximación decimal del número \(\pi\), mientras que el paquete SymPy lo trata de forma simbólica al ser un número irracional.

Lo mismo puede observarse si se utiliza la función de cálculo de raíces cuadradas (sqrt) o las funciones trigonométricas habituales:

np.sqrt(2)

1.4142135623730951

sp.sqrt(2)
\[\displaystyle \sqrt{2}\]
np.sin(np.pi/4)

0.7071067811865476

sp.sin(sp.pi/4)
\[\displaystyle \frac{\sqrt{2}}{2}\]

Aunque SymPy trabaja por defecto en modo simbólico exacto, también es posible solicitar que los resultados se aproximen con valores decimales. Para ello se dispone de la función evalf() que se puede aplicar tras una expresión simbólica, tal como se hace en este ejemplo:

sp.sin(sp.pi/4).evalf()
\[\displaystyle 0.707106781186548\]

Una de las ventajas de las funciones definidas en el paquete Numpy es la posibilidad de aplicarlas sobre los elementos de una lista. De esta manera en una única operación se puede evaluar la función sobre un conjunto amplio de valores.

np.sqrt([0.1, 0.23, 0.35, 0.57, 0.61, 0.89, 0.93])

array([0.31622777, 0.47958315, 0.59160798, 0.75498344, 0.78102497,
       0.94339811, 0.96436508])

Datos y variables en Python#

Los elementos básicos sobre los que trabaja el cálculo diferencial son la definición de variables numéricas y funciones. En Python se pueden trabajar con datos numéricos de diferentes tipos: enteros (int), decimales (float) o incluso complejos (complex). Esos datos, para ser utilizados posteriormente, deben ser almacenados en las variables, que actúan como contenedores de datos. Además, tanto datos como variables pueden ser combinadas en expresiones haciendo uso de operadores. En este caso es importante tener en cuenta la prioridad en el orden de aplicación de los operadores y utilizar los paréntesis si se desea variar dicho orden.

Algunas características destacadas del tratamiento de variables en Python son:

  • No es preciso declararlas previamente, basta con realizar una asignación directa del valor.

  • Las variables son de tipado dinámico, lo que significa que adaptan su tipo a lo que contengan en cada momento

  • Los operadores pueden realizar operaciones diferentes en función del tipo de dato o variable sobre el que se apliquen.

A la hora de utilizar nombres para las variables hay que tener en cuenta algunas normas y recomendaciones:

  • Un identificador puede ser cualquier combinación de letras (mayúsculas y minúsculas), números y el carácter de subrayado

  • No puede comenzar por un número ni coincidir con palabras reservadas del lenguaje

  • Se distinguen las mayúsculas de las minúsculas

  • Se recomienda el uso de nombres expresivos

Para asignar un valor a una variable se utiliza el operador =, pudiéndose asignar un valor literal, una expresión o la llamada a una función. En Python es posible asignar un mismo valor a varias variables en una sola sentencia o varias asignaciones diferentes en la misma sentencia. Los siguientes ejemplos ilustran todo lo comentado en relación a la definición de variables

A = 2*5+3
B = 2*(5+3)
print(A,B)

13 16

Respecto a los operadores aritméticos, quizás lo único que convendría advertir es que el operador de potenciación (elevado a) se señala con dos asteriscos **

2**5

32

En el caso de números en notación científica, no es necesario utilizar el operador de potenciación, permitiéndose la notación habitual usando la letra e o E (en este caso sí que es indiferente el uso de mayúscula o minúscula).

x = y = 0
u, v, w = 0.03, 6.17e6, 0.12e-3

Respecto a las variables complejas, debe tenerse en cuenta que la unidad imaginaria se denota por j. Por ejemplo, a continuación se muestra un ejemplo de expresión con números complejos:

z1 = 2+3j
z2 = 5-1j
z3 = -1-2j
z1*(z2+z3)/(z2+1)

(2.5945945945945943+1.4324324324324322j)

Un intento de uso como identificador de variable de una palabra reservada del lenguaje daría un error. En caso de duda, importando el paquete keyword se podría tener acceso a todas esas palabras reservadas

import keyword
keyword.kwlist

['False',
 'None',
 'True',
 '__peg_parser__',
 'and',
 'as',
 'assert',
 'async',
 'await',
 'break',
 'class',
 'continue',
 'def',
 'del',
 'elif',
 'else',
 'except',
 'finally',
 'for',
 'from',
 'global',
 'if',
 'import',
 'in',
 'is',
 'lambda',
 'nonlocal',
 'not',
 'or',
 'pass',
 'raise',
 'return',
 'try',
 'while',
 'with',
 'yield']

Por ejemplo, la palabra in está reservada por el lenguaje, por lo que su uso como nombre de variable no estaría permitido.

keyword.iskeyword("in")

True

Debe destacarse que en el caso de asignar un valor a una variable, esta asignación permanece durante toda la sesión a no ser que se cambie o se borre explicitamente. Para eliminar de manera explícita una variable se usa la sentencia del. En relación a los posibles cambios de valores, una variable puede pasar a contener un valor de otro tipo, ajustando automáticamente su tipo al correspondiente al valor asignado; es decir, Python usa tipado dinámico, sin embargo no realiza conversiones implícitas de tipos.

del z1, z2, z3

Precisamente, el tema de las conversiones de tipo es algo que hay que tener muy presente, porque el efecto de los operadores puede variar dependiendo del tipo de dato. Por ejemplo, el operador + sobre datos numéricos realiza la suma, pero sobre datos de tipo alfanumérico realiza concatenaciones de cadenas de caracteres. Esto es especialmente importante cuando un programa Python solicita datos de entrada a través de la instrucción input ya que los datos se almacenan como texto. Se puede comprobar en este sencillo ejemplo:

n = input('Primer número a sumar:')
m = input('Segundo número a sumar:')
suma = n + m
print('El valor de la suma es', suma)

El valor de la suma es 23

En este caso habría sido necesario hacer una conversión explícita previa de los datos a número entero (int) o decimal (float), según se desee, porque si no se hace los datos se tratan como cadenas de caracteres y en ese caso el operador + actúa como concatenador de cadenas.

n = float(input('Primer número a sumar:'))
m = float(input('Segundo número a sumar:'))
suma = n + m
print('El valor de la suma es', suma)

El valor de la suma es 5.0

El paquete SymPy permite definir variables simbólicas y realizar operaciones con ellas sin necesidad de especificar ningún valor. Esta posibilidad es interesante para trabajar en diferentes modelos matemáticos que puedan depender de parámetros.

import sympy as sp
x = sp.Symbol('x') 
y = sp.Symbol('y') 
x**2 + 2*x*y + 1
\[\displaystyle x^{2} + 2 x y + 1\]

De hecho, una de las posibilidades de este paquete de cálculo simbólico es realizar operaciones de derivación simbólica:

sp.diff(x**2 + 2*x*y + 1, x)
\[\displaystyle 2 x + 2 y\]
sp.diff(x**2 + 2*x*y + 1, y)
\[\displaystyle 2 x\]

Funciones y expresiones funcionales en Python#

El cálculo diferencial se basa principalmente en trabajar con funciones y definir sobre ellas diferentes operaciones (estudio de límites, derivación, optimización, integración,…)

En Python, por supuesto, se pueden definir funciones, tanto de una única variable como multivariadas. En el contexto de este curso de cálculo diferencial avanzado nos centraremos especialmente en estas últimas, las funciones de varias variables.

En este curso, se trabajará tanto con funciones como con expresiones simbólicas funcionales. Como se verá en los próximos ejemplos, son conceptos diferentes y que requieren un tratamiento diferente.

Una expresión funcional estará definida a partir de variables simbólicas, usando las posibilidades que nos ofrece el paquete de cálculo simbólico SymPy. En cambio, las funciones responden al esquema más clásico de definición de funciones en programación. Toda función se va a caracterizar por:

  • Un nombre, que debe cumplir las mismas condiciones que los nombres de variables.

  • Una posible lista de argumentos, pudiéndose incluso definir argumentos opcionales con valores por defecto

  • Un valor o valores devueltos. En Python una función puede devolver varios valores, incluso de diferentes tipos.

Para definir funciones en Python se puede utilizar la sentencia def o recurrir al uso de las conocidas como expresiones lambda, en este caso, no es necesario dar el nombre a la función.

A continuación se muestran algunos ejemplos de la definición de funciones y expresiones funcionales en Python.

Ejemplo:

Se desea definir la función real de variable real

\[f(x)=x\cos(\frac{1}{x^2+1})\]

Una primera alternativa sería definir una expresión simbólica a partir de un símbolo x. Para ello hay que usar las prestaciones del paquete SymPy

import sympy as sp
x = sp.Symbol('x')
fsim = x*sp.cos(1/(x**2+1))

La ventaja de la definición de una expresión simbólica es que resulta sencillo aplicar operaciones como la derivación mediante métodos que se pueden aplicar sobre expresiones simbólicas. Por ejemplo, la derivada de la función \(f(x)\) se podría calcular de dos maneras:

fsim.diff(x)
\[\displaystyle \frac{2 x^{2} \sin{\left(\frac{1}{x^{2} + 1} \right)}}{\left(x^{2} + 1\right)^{2}} + \cos{\left(\frac{1}{x^{2} + 1} \right)}\]
sp.diff(fsim,x)
\[\displaystyle \frac{2 x^{2} \sin{\left(\frac{1}{x^{2} + 1} \right)}}{\left(x^{2} + 1\right)^{2}} + \cos{\left(\frac{1}{x^{2} + 1} \right)}\]

De igual manera se podrían calcular derivadas de orden superior, por ejemplo \(f''(x)\):

fsim.diff(x,2).simplify()
\[\displaystyle - \frac{2 x \left(x^{4} \sin{\left(\frac{1}{x^{2} + 1} \right)} + 2 \sqrt{2} x^{2} \sin{\left(\frac{\pi}{4} - \frac{1}{x^{2} + 1} \right)} - 3 \sin{\left(\frac{1}{x^{2} + 1} \right)}\right)}{\left(x^{2} + 1\right)^{4}}\]
sp.diff(fsim, (x,2))
\[\displaystyle \frac{2 x \left(- \frac{4 x^{2} \sin{\left(\frac{1}{x^{2} + 1} \right)}}{x^{2} + 1} - \frac{2 x^{2} \cos{\left(\frac{1}{x^{2} + 1} \right)}}{\left(x^{2} + 1\right)^{2}} + 3 \sin{\left(\frac{1}{x^{2} + 1} \right)}\right)}{\left(x^{2} + 1\right)^{2}}\]

El inconveniente de la definición de expresiones funcionales simbólicas es que la evaluación de la función no se puede realizar directamente, se necesita un proceso de sustición explícita de la variable simbólica por un valor. Por ejemplo, para calcular \(f(0)\) y \(f(\pi)\) habría que proceder de la siguiente manera:

fsim.subs({x:0})
\[\displaystyle 0\]
fsim.subs({x:sp.pi})
\[\displaystyle \pi \cos{\left(\frac{1}{1 + \pi^{2}} \right)}\]

Como se observa, el resultado de la evaluación de la expresión funcional se expresa también en forma simbólica. Si se desea obtener una aproximación numérica de ese resultado puede aplicarse la opción evalf() al final de la expresión y precedida de un punto:

fsim.subs({x:sp.pi}).evalf()
\[\displaystyle 3.1283069041166\]

La alternativa al uso de una expresión funcional simbólica, sería la definición de una función numérica, que además podría ser evaluada de forma directa.

import numpy as np
def fnum(x): return(x*np.cos(1/(x**2+1)))

fnum(0)

0.0

fnum(np.pi)

3.1283069041165987

Sin embargo, estas funciones numéricas no pueden ser objeto de aplicación de operaciones simbólicas como la del cálculo de derivadas.

Una ventaja de las funciones numéricas es que su representación gráfica se puede hacer más fácilmente con ayuda de otro de los paquetes que se utilizarán con frecuencia: el paquete Matplotlib.

Para obtener la representación gráfica de la función hay que definir un array de valores de la variable independiente (\(x\)) con sus respectivos valores de \(y=f(x)\). El siguiente código muestra cómo hacerlo:

import matplotlib.pyplot as plt
x = np.linspace(0,1)
y = fnum(x)
plt.plot(x,y)
plt.show()
_images/9736bf8dc55e170f40d784c04031f06dcb32ac2999a760a22e87758cd082705b.png

Python ofrece otra alternativa para trabajar con funciones: la posibilidad de definir funciones numéricas sin asignarles ningún nombre (expresiones lambda). Su utilización para evaluar alguna expresión, exigiría al menos asignar la definición de función a una variable. Esa variable puede ser utilizada, por ejemplo, para pasar la función como argumento a otras funciones.

La función de este ejemplo se podría definir también de esta forma:

fl = lambda x: x*np.cos(1/(x**2+1))

Como la función se ha asignado a una variable fl, podría también evaluarse en puntos del dominio:

fl(0)

0.0

fl(np.pi)

3.1283069041165987

Ejemplo:

Igual que se pueden definir funciones de una variable, también es posible hacerlo con funciones que tengan dos o más argumentos. Por ejemplo la función \(F(x,y)=e^{x^2+y^2}-\frac{2x+3y}{5}\) podría definirse como expresión simbólica, función numérica o expresión lambda:

x,y = sp.symbols('x,y')
Fsim = sp.exp(x**2+y**2)-(2*x+3*y)/5

def Fnum(x,y): return(np.exp(x**2+y**2)-(2*x+3*y)/5)

FL = lambda x,y: np.exp(x**2+y**2)-(2*x+3*y)/5

La evaluación de la función en un punto se haría de manera diferente dependiendo de cómo se haya definido la función:

Fsim.subs({x:1, y:2})
\[\displaystyle - \frac{8}{5} + e^{5}\]
Fnum(1,2)

146.8131591025766

FL(1,2)

146.8131591025766
Cuando la definición de la función sea un poco más compleja, puede ser recomendable no hacerlo en una sola línea de código sino utilizar un bloque de código indentado a continuación del signo `:` que señala el inicio de la definición de la función.

Ejemplo:

Se desea definir la siguiente función

\[\begin{split}G(x,y)=\left\{\begin{array}{ll}\frac{1}{x^2+y^2-1} & si\; x^2+y^2<1\\ 1 & si\; x^2+y^2\geq 1\\ \end{array}\right.\end{split}\]

En primer lugar, como expresión funcional simbólica se podría definir con ayuda de la función Piecewise() que tiene el paquete SymPy:

Gsim =  sp.Piecewise( ( 1/(x**2+y**2-1),     (x**2+y**2<1)),
                      ( 1,                   (x**2+y**2>=1)) )

Gsim.subs({x:1/2, y:1/2})
\[\displaystyle -2.0\]

Como función numérica podría definirse de dos maneras:

def Gnum(x,y):
    aux = x**2+y**2
    if (aux<1):
        return(1/(aux-1))
    else:
        return(1)

Gnum(1/2, 1/2)

-2.0

GL = lambda x,y: 1/(x**2+y**2-1) if(x**2+y**2<1) else 1

GL(1/2, 1/2)

-2.0

Ejemplo:

Un nuevo ejemplo es la función

\[\begin{split}h(x)=\left\{\begin{array}{ll}-1 & si\; x\leq 0\\ 2x+1 & si\; x\in(0,1)\\ x^2-1 & si\;x\geq 1\end{array}\right.\end{split}\]

que podria definirse en Python de las siguientes maneras:

x = sp.Symbol('x')
hsim = sp.Piecewise( ( -1,     (x<=0) ),
                     ( 2*x+1,  ((x>0)&(x<1)) ),
                     ( x**2-1, (x>=1) ) )

hsim.subs({x:2})
\[\displaystyle 3\]
def hnum(x):
    if x<=0:
        return -1
    elif x<1:
        return 2*x+1
    else:
        return x**2-1

hnum(2)

3

hl = lambda x: -1 if x <= 0 else (2*x + 1 if x < 1 else x**2 - 1)

hl(2)

3

Con estas nociones básicas de la forma de trabajar con variables y funciones en Python, ya se estaría en condiciones de afrontar esta asignatura de ampliación del cálculo diferencial básico. El objetivo será ir descubriendo poco a poco los diferentes conceptos al mismo tiempo que se adquieren las destrezas necesarias para resolver, tanto de forma manual como con ayuda de Python, diferentes problemas prácticos.

Los próximos cuadernos computacionales estarán destinados a abordar los temas que forman parte del programa de la asignatura:

  • Integración múltiple

  • Integrales de línea y de superficie

  • Ecuaciones diferenciales

  • Transformadas integrales