Introducción a las ecuaciones diferenciales ordinarias

Las ecuaciones diferenciales constituyen uno de los instrumentos de mayor aplicabilidad práctica de la matemática aplicada. Muchos de los problemas que surgen en diferentes campos de la ingeniería vienen modelizados mediante ecuaciones diferenciales, por lo que resulta interesante conocerlas y saber resolver las ecuaciones más importantes. En esta parte del curso se presentan algunas de las ecuaciones diferenciales de primer orden más importantes, las ecuaciones lineales de coeficientes constantes y los sistemas de ecuaciones diferenciales. Además se finaliza con una rápida introducción a las ecuaciones en derivadas parciales.

Desde el punto de vista de la resolución de las ecuaciones, se verá cómo resolver algunas de las más habituales mediante técnicas analíticas y se mostrará igualmente la resolución mediante métodos numéricos de aproximación, todo ello con ayuda de los paquetes específicos de Python.

Concepto de ecuación diferencial y ejemplos de aplicación

Dada una función \(f(x)\), su derivada \(f'(x)=\frac{df}{dx}\) es una nueva función que guarda cierta relación con la función original. Así por ejemplo, si \(f(x)=xe^{x^2}\) entonces

\[f'(x)=e^{x^2}+2x^2e^{x^2}=(1+2x^2)e^{x^2}\]

En definitiva, llamando \(y=f(x)\), se cumpliría la relación

\[y'=(1+2x^2)\frac{y}{x}\]

La expresión anterior es un ejemplo de ecuación diferencial, es decir, una ecuación que relaciona el valor de la función y sus derivadas con el de la variable independiente.

El objetivo de esta parte del curso será conocer y saber aplicar métodos que permitan invertir el proceso anterior, es decir, ser capaces de deducir la forma general de la función \(y\) a partir de una ecuación en la que está implicada la función y sus derivadas.

Resolver ecuaciones diferenciales puede considerarse como una generalización del cálculo de primitivas, ya que calcular primitivas es un caso particular de resolución de ecuación diferencial sencilla. Por ejemplo, la solución de la ecuación diferencial

\[y'=2x+\cos(x)\]

sería

\[y=\int(2x+\cos(x))dx=x^2+\sin(x)+c\]

donde \(c\) es una constante arbitraria. Como puede comprobarse, la solución general de una ecuación diferencial no es única, sino que depende de una o varias constantes arbitrarias.

Ecuación diferencial:

Una ecuación diferencial es una ecuación que relaciona una función (o variable dependiente), su variable o variables (variables independientes), y sus derivadas. Si la ecuación contiene derivadas respecto a una sola variable independiente entonces se dice que es una ecuación diferencial ordinaria (EDO); y si contiene las derivadas parciales respecto a dos o más variables independientes se llama ecuación en derivadas parciales (EDP).

Ejemplos de ecuaciones diferenciales ordinarias son:

\[y'-5xy+2=0,\;\;\;\;\;\;\;\;\;(x^2+y)dx-(2x-y)dy=0,\;\;\;\;\;\;\;\;\;\frac{dy}{dx}=\frac{y-1}{x}\]

\[y''-3xy'+6y=8,\;\;\;\;\;\;\;\;\;\frac{d^4y}{dx^4}-4\frac{d^3y}{dx^3}+5\frac{d^2y}{dx^2}-2\frac{dy}{dx}-3y=x\]

mientras que un ejemplo de ecuación en derivadas parciales sería:

\[x\frac{\partial u}{\partial x}+y\frac{\partial u}{\partial y}=u\]

Orden de una ecuación diferencial:

En una ecuación diferencial pueden intervenir derivadas de cualquier orden, de manera que se llama orden de la ecuación diferencial al orden de la derivada o derivada parcial más alta que aparece en la ecuación.

Como se ha visto en los ejemplos previos, una ecuación diferencial admite diferentes formas de expresión. En el caso de las ecuaciones diferenciales ordinarias se puede distinguir entre ecuaciones en forma implícita y explícita:

• Una ecuación diferencial de orden \(n\) está expresada en forma implícita cuando tiene la forma

\[F(x,y,y',y'',\dots,y^{(n)})=0\]

• Una ecuación diferencial de orden \(n\) está expresada en forma explícita cuando tiene la forma

\[y^{(n)}=G(x,y,y',y'',\dots,y^{(n-1)})\]

Un tipo especial de ecuaciones diferenciales que aparecen en gran número de modelos prácticos en la ingeniería es el constituido por las denominadas ecuaciones lineales.

Ecuación diferencial lineal:

Se dice que una ecuación diferencial es lineal cuando tiene la forma

\[a_n(x)y^{(n)}+a_ {n-1}(x)y^{(n-1)}+\dots+a_2(x)y''+a_1(x)y'+a_0(x)y=g(x)\]

Cuando \(g(x)=0\) la ecuación se dice homogénea. Un tipo especial de ecuaciones lineales, y que resultan más sencillas de resolver, son aquellas en las que los coeficientes son constantes, es decir, \(a_i(x)=a_i\in R\).

Las ecuaciones diferenciales surgen en la modelización de una gran variedad de problemas físicos e ingenieriles. A continuación se indican las ecuaciones que rigen algunos fenómenos conocidos:

• Desintegración radiactiva: la rapidez con la que una sustancia radiactiva se desintegra es proporcional a la cantidad presente de dicha sustancia. Si \(A(t)\) representa la cantidad de sustancia presente en un instante \(t\), y \(k>0\) es la constante de proporcionalidad, la ecuación diferencial correspondiente es:

\[\frac{dA}{dt}=-kA\]

• Enfriamiento de un cuerpo: la ley de enfriamiento de Newton establece que la velocidad de enfriamiento de un cuerpo es proporcional a la diferencia de temperaturas entre él y el medio que lo rodea. Asumiendo que \(T_a\) es la temperatura fija del medio circundante, esta propiedad determina la siguiente ecuación diferencial:

\[\frac{dT}{dt}=k(T-T_a)\]

• Cuerpo en caída libre: la altura sobre el suelo \(h(t)\) en un instante \(t\) de un cuerpo que cae por efecto de la gravedad, viene definida por la siguiente ecuación diferencial de grado 2:

\[\frac{d^2h}{dt^2}=-g\]

• Oscilador armónico: dada una masa \(m\) colgada a un resorte, si \(y(t)\) es la distancia a la posición de equilibrio, y \(k\) la constante de elasticidad del resorte, el movimiento de la masa viene regulado por la siguiente ecuación:

\[m\frac{d^2y}{dt^2}=-ky\]

• Si se considera el caso de un oscilador armónico amortiguado, en el que hay una fuerza adicional que frena el movimiento y que es proporcional a la velocidad, la ecuación diferencial sería:

\[m\frac{d^2y}{dt^2}=-ky-b\frac{dy}{dt}\]

Soluciones de una ecuación diferencial

Solución de una ecuación diferencial:

Dada una ecuación \(F(x,y,y',y'',\dots,y^{(n)})=0\), se dice que una función \(y=\phi(x)\) es una solución de la ecuación en un intervalo \(I\) cuando

\[F(x,\phi(x),\phi'(x),\phi''(x),\dots,\phi^{(n)}(x))=0\;\;\;\forall x\in I\]

---

Ejemplo:

La función \(y=\phi(x)=e^{2x}\) es una solución de la ecuación

\[y''-4y'+4y=0\]

Efectivamente, si \(y=e^{2x}\) entonces

\[y' = 2e^{2x}; \;\;\;\;\;\;\;\; y'' = 4e^{2x}\]

que sustituido en la ecuación, conduce a

\[y''-4y'+4y = 4e^{2x} -8e^{2x} +4e^{2x} = 0\]

---

Las soluciones de una ecuación diferencial pueden venir dadas como una función o una expresión que verifica la ecuación. Se dice que una solución es explícita cuando es una expresión de la forma \(y = y(x)\), mientras que se dice solución implícita cuando viene dada por una expresión de la forma \(g(x, y) = 0\).

---

Ejemplo:

La expresión \(y^2-x^3+8=0\) define implícitamente una solución de la ecuación

\[y'=\frac{3x^2}{2y}\]

Se puede comprobar simplemente derivando implícitamente:

\[2yy'-3x^2=0\]

y despejando el valor de \(y'\) en la expresión anterior.

---

En general, si una ecuación diferencial tiene solución, entonces realmente tiene toda una familia de soluciones dependiendo de tantas constantes arbitrarias como el orden de la ecuación. Esta norma no siempre es cierta, pero para la mayor parte de las ecuaciones que se considerarán sí que puede considerarse válida.

---

Ejemplo:

Dada la ecuación diferencial de grado 2:

\[y''=e^x-x\]

integrando una vez se obtendría

\[y'=e^x-\frac{x^2}{2}+C_1\]

e integrando de nuevo se obtiene la solución general de la ecuación

\[y=e^x-\frac{x^3}{6}+C_1x+c_2\]

Como puede apreciarse, la solución general depende de dos constantes arbitrarias, es decir, es una familia paramétrica de funciones.

---

Ejemplo:

La ecuación diferencial

\[(y')^2+2y^2=0\]

es de grado 1, pero únicamente tiene como solución la función \(y=0\).

---

En ocasiones pueden existir soluciones singulares, que no contienen constantes arbitrarias y no están contenidas en la familia paramétricas de funciones. Es lo que ocurre en el siguiente caso.

---

Ejemplo:

Dada la ecuación

\[\frac{dy}{dx}=\sqrt{y}\]

para encontrar sus soluciones se podría expresar la ecuación en la forma:

\[\frac{dy}{\sqrt{y}}=dx\]

y haciendo una doble integración se obtendría

\[\int\frac{dy}{\sqrt{y}}=\int dx\Longrightarrow 2\sqrt{y}=x+C\]

o equivalentemente

\[\sqrt{y}=\frac{x+C}{2}\]

donde \(C\) es una constante arbitraria. Esta solución está definida para \(x\in[-C,+\infty]\).

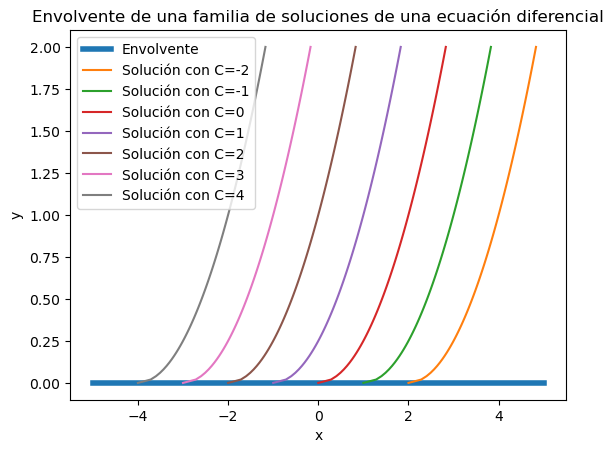
Sin embargo hay otra solución singular que no aparece incluida dentro de esa familia de soluciones, la solución \(y=0\). Realmente esta solución singular es la envolvente a la familia paramétrica. Se llama envolvente de una familia de curvas a una curva que es tangente a toda la familia y que en cada punto de la envolvente existe un único miembro de la familia tangente a ella.

En la siguiente figura generada con ayuda de Python puede verse como la recta \(y=0\) es la envolvente de la familia paramétrica de soluciones de la ecuación.

import matplotlib.pyplot as plt
import numpy as np
y = np.linspace(0,2,100)
x_valores = [2*np.sqrt(y)-C for C in [-2, -1, 0, 1, 2, 3, 4]]

# Representación gráfica de las soluciones
x = np.linspace(-5,5)
plt.plot(x, np.zeros_like(x), linewidth=4, label='Envolvente')
for C, x in enumerate(x_valores):
    plt.plot(x, y, label=f'Solución con C={-2 + C}')

plt.title('Envolvente de una familia de soluciones de una ecuación diferencial')
plt.xlabel('x'); plt.ylabel('y')
plt.legend()
plt.show()

Soluciones analíticas de ecuaciones diferenciales con Python

La resolución analítica de una ecuación diferencial puede intentarse con una funcionalidad del paquete especializado en computación simbólica SymPy. Además de las opciones de integración de este paquete que ya han sido analizadas, SymPy proporciona un solucionador genérico de ecuaciones diferenciales ordinarias (EDO), sympy.dsolve, el cual es capaz de encontrar soluciones analíticas a muchas ecuaciones diferenciales elementales. Sin embargo, debe advertirse que la mayoría de las ecuaciones no se pueden resolver analíticamente y deberán ser abordadas desde un punto de vista numérico.

Antes de analizar diferentes ejemplos, se necesia cargar el paquete y definir la variable independiente (\(x\)) como objeto Symbol y la función \(y(x)\) como un objeto de función simbólica Funtion.

import sympy as sp
x = sp.Symbol('x')
y = sp.Function('y')

A partir de ese momento ya pueden definirse ecuaciones simbólicas (objetos Eq) y resolverlas con la funcion dsolve(). Pero antes conviene aclarar que para derivar una función simbólica y(x) debe usarse la instrucción y(x).diff(x,n) siendo n el orden de derivación (por defecto es 1).

Otra advertencia importante es que cualquier referencia a la función tendría que hacerse señalando necesariamente su argumento entre paréntesis, es decir, siempre en la forma y(x).

y(x).diff(x)

\[\displaystyle \frac{d}{d x} y{\left(x \right)}\]

y(x).diff(x,2)

\[\displaystyle \frac{d^{2}}{d x^{2}} y{\left(x \right)}\]

Se incluyen a continuación las resoluciones con Python de las ecuaciones planteadas en los ejemplos anteriores:

• Ecuación \(y''-4y'+4y=0\)

sp.Eq(y(x).diff(x,2)-4*y(x).diff(x)+4*y(x), 0)

\[\displaystyle 4 y{\left(x \right)} - 4 \frac{d}{d x} y{\left(x \right)} + \frac{d^{2}}{d x^{2}} y{\left(x \right)} = 0\]

ecuacion = sp.Eq(y(x).diff(x,2)-4*y(x).diff(x)+4*y(x), 0)
sp.dsolve(ecuacion)

\[\displaystyle y{\left(x \right)} = \left(C_{1} + C_{2} x\right) e^{2 x}\]

• Ecuación \(y'=\frac{3x^2}{2y}\)

ecuacion = sp.Eq(y(x).diff(x), 3*x**2/(2*y(x)))
sp.dsolve(ecuacion)

[Eq(y(x), -sqrt(C1 + x**3)), Eq(y(x), sqrt(C1 + x**3))]

• Ecuación \(y''=e^x-x\)

ecuacion = sp.Eq(y(x).diff(x,2), sp.exp(x)-x)
sp.dsolve(ecuacion)

\[\displaystyle y{\left(x \right)} = C_{1} + C_{2} x - \frac{x^{3}}{6} + e^{x}\]

• Ecuación \((y')^2+2y^2=0\)

ecuacion = sp.Eq(y(x).diff(x)**2+2*y(x)**2, 0)
sp.dsolve(ecuacion)

[Eq(y(x), C1*exp(-sqrt(2)*I*x)), Eq(y(x), C1*exp(sqrt(2)*I*x))]

• Ecuación \(\frac{dy}{dx}=\sqrt{y}\)

ecuacion = sp.Eq(y(x).diff(x), sp.sqrt(y(x)))
sp.dsolve(ecuacion)

\[\displaystyle y{\left(x \right)} = \frac{C_{1}^{2}}{4} + \frac{C_{1} x}{2} + \frac{x^{2}}{4}\]

---

Ejemplo:

A la hora de resolver simbólicamente EDO puede definirse previamente el objeto ecuación (Eq) o introducir las expresiones simbólicas de la ecuación directamente en la función de resolución, siempre que a la derecha de la ecuación se tenga solo una función simbólica o valor constante.

Por ejemplo, la resolución de la ecuación \(y'=-3x^2y+6x^2\) con SymPy podría hacerse de las dos formas siguientes:

x = sp.Symbol('x')
y = sp.Function('y')
ecuacion = sp.Eq(y(x).diff(x), 6*x**2 - 3*x**2*(y(x)))
sp.dsolve(ecuacion)

\[\displaystyle y{\left(x \right)} = C_{1} e^{- x^{3}} + 2\]

x = sp.Symbol('x')
y = sp.Function('y')
sp.dsolve(y(x).diff(x) - 6*x**2 + 3*x**2*(y(x)), 0)

\[\displaystyle y{\left(x \right)} = C_{1} e^{- x^{3}} + 2\]

---

Ejemplo:

La resolución simbólica de la ecuación

\[3x\frac{dy}{dx}-(x^2-9)y=-\frac{1}{x}\]

es

x = sp.Symbol('x')
y = sp.Function('y')
edo = sp.Eq(3*x*y(x).diff(x) - (x**2-9)*y(x), -1/x)
sp.dsolve(edo)

\[\displaystyle y{\left(x \right)} = \frac{C_{1} e^{\frac{x^{2}}{6}} + 1}{x^{3}}\]

x = sp.Symbol('x')
y = sp.Function('y')
sp.dsolve(3*x*y(x).diff(x) - (x**2-9)*y(x) + 1/x)

\[\displaystyle y{\left(x \right)} = \frac{C_{1} e^{\frac{x^{2}}{6}} + 1}{x^{3}}\]

El problema de valor inicial

En general la solución de una ecuación diferencial depende de un conjunto de constantes arbitrarias. Para determinar una solución única se necesita por tanto especificar una serie de condiciones adicionales.

En el caso de ecuaciones de primer orden, se conoce como problema de valor inicial a un problema de la forma:

\[\begin{split} \left\{ \begin{array}{l} \frac{dy}{dx}=f(x,y)\\ y(x_0)=y_0 \end{array} \right.\end{split}\]

Una pregunta obvia que se puede plantear es si se tiene garantizada la existencia de solución del problema de valor inicial, y si dicha solución es única. Se puede asegurar la existencia y unicidad de solución del problema de valor inicial en un entorno del punto \(x_0\) si tanto \(f(x,y)\) como \(\frac{\partial f}{\partial y}\) son funciones continuas en un entorno del punto \((x_0,y_0)\).

En el caso de ecuaciones de orden \(n\), para determinar los valores de las constantes arbitrarias que aparecen en la familia paramétrica de soluciones se necesitarían \(n\) condiciones iniciales. Así, el problema de valor inicial para una ecuación de orden \(n\) es:

\[\begin{split} \left\{ \begin{array}{l} F(x,y,y',y'',\dots,y^{(n)})=0\\ y(x_0)=y_0,\;y'(x_0)=y_1,\;y''(x_0)=y_2,\dots,y^{(n)}(x_0)=y_n \end{array} \right. \end{split}\]

---

Ejemplo:

La solución general de la ecuación

\[y´+2y=x+2x^2\]

es

\[y = C e^{-2x} + x^{2} - \frac{x}{2} + \frac{1}{4}\]

Si se considera el problema de valor inicial

\[\begin{split}\left\{ \begin{array}{l} y´+2y=x+2x^2\\ y(0)=4 \end{array} \right.\end{split}\]

la constante tomaría el valor \(C=\frac{15}{4}\) ya que se tendria que cumplir \(y(0)=C+\frac{1}{4}=4\), por lo que la solución del problema de valor inicial sería:

\[y = \frac{15}{4}e^{-2x} + x^{2} - \frac{x}{2} + \frac{1}{4}\]

Este proceso de determinación de valores para las constantes arbitrarias puede realizarse también con la función de resolución simbólica de ecuaciones en Python.

La solución general de la ecuación puede obtenerse de la siguiente forma:

x = sp.Symbol('x')
y = sp.Function('y')
edo = sp.Eq(y(x).diff(x) + 2*y(x), x + 2*x**2)
sp.dsolve(edo)

\[\displaystyle y{\left(x \right)} = C_{1} e^{- 2 x} + x^{2} - \frac{x}{2} + \frac{1}{4}\]

Pero si lo que se quiere es resolver el problema de valor inicial, la condición puede indicarse dentro del parámetro opcional ics que acepta la función dsolve

x = sp.Symbol('x')
y = sp.Function('y')
edo = sp.Eq(y(x).diff(x) + 2*y(x), x + 2*x**2)
condicion = {y(0):4}
sp.dsolve(edo, ics=condicion)

\[\displaystyle y{\left(x \right)} = x^{2} - \frac{x}{2} + \frac{1}{4} + \frac{15 e^{- 2 x}}{4}\]

---

Ejemplo:

La solución general de la ecuación

\[y''+y=0\]

es

\[y=C_1\cos x + C_2\sin x\]

Si se considera el problema de valor inicial

\[\begin{split}\left\{ \begin{array}{l} y''+y=0\\ y(0)=-1,\;y'(0)=1 \end{array} \right. \end{split}\]

las constantes tomarían los valores \(C_1=-1\) y \(C_2=1\), por lo que la solución del problema de valor inicial sería:

\[y=-\cos x + \sin x\]

La resolución directa del problema de valor inicial con ayuda de Python se haría de la siguiente manera:

x = sp.Symbol('x')
y = sp.Function('y')
edo = sp.Eq(y(x).diff(x,2) + y(x), 0)
condicion = {y(0):-1, y(x).diff(x).subs(x,0):1}
sp.dsolve(edo, ics=condicion)

\[\displaystyle y{\left(x \right)} = \sin{\left(x \right)} - \cos{\left(x \right)}\]

Ejercicios propuestos

• Comprobar que las siguientes funciones \(\phi(x)\) son soluciones de las respectivas ecuaciones diferenciales:

  • \(\phi(x)=x^2-\frac{1}{x}\) para la ecuación \(y''-\frac{2}{x^2}y=0\)

  • \(\phi(x)=e^{-x}+3e^{2x}\) para la ecuación \(y''-y'-2y=0\)

  • \(\phi(x)=\frac{x^4}{16}\) para la ecuación \(y'-xy^{1/2}=0\)

• Calcular la solución general de las siguientes ecuaciones diferenciales:

\[y'=x^2\]

\[y''=\cos 2x\]

\[y'''=24x\]

• Comprobar que la función \(y=3e^{2x}+e^{-2x}-3x\) es solución del problema de valor inicial

\[\begin{split}\left\{ \begin{array}{l} y''-4y=12x\\ y(0)=4,\;y'(0)=1 \end{array} \right. \end{split}\]

• Comprobar que \(y=Ce^{-x^2}\) es la solución general de la ecuación \(\frac{dy}{dx}+2xy=0\) y posteriormente encontrar la solución que pasa por el punto \((x_0,y_0)=(2,2)\)

• Comprobar que las funciones \(y_1(x)=2\) e \(y_2(x)=2\cos x\) son ambas soluciones del siguiente problema de valor inicial para \(x\in[0,\pi]\) y que dicho problema no verifica las condiciones exigidas para la existencia y unicidad de solución.

\[\begin{split}\left\{ \begin{array}{l} y'+(4-y^2)^{1/2}=0\\ y(0)=2 \end{array} \right. \end{split}\]