Introducción a la integración múltiple

Gran parte de los problemas que surgen en la ingeniería vienen modelizados por funciones de más de una variable, por lo que se hace necesario generalizar el concepto de integral definida de funciones de una variable para abordar la integración de funciones de la forma \(f:D\subseteq R^n\rightarrow R\). En particular, en este primer tema se analizarán los casos de \(n=2\) y \(n=3\), introduciendo los conceptos de integrales dobles y triples, su interpretación, sus métodos de cálculo y presentando diferentes aplicaciones prácticas.

Pero antes convendría recordar el concepto de integral definida en funciones de una variable.

Integral definida de funciones de una variable

Dada una función de una variable \(f(x)\) definida en un intervalo cerrado \([a,b]\), la integral

\[\int_a^b f(x)dx\]

representa el área que queda comprendida debajo de la curva y entre \(x=a\) y \(x=b\), y puede ser calculado mediante las conocidas como sumas de Riemann de la siguiente manera:

\[\int_a^b f(x)dx= \lim_{\Delta x_i\rightarrow 0}\sum_{i=1}^n f(x_i^*)\Delta x_i\]

donde \(\{x_0,x_1,x_2,\dots,x_n\}\) es una partición de \([a,b]\) con \(a=x_0<x_1<x_2<\dots<x_n=b\) y \(\Delta x_i=x_{i-1}-x_i\). El punto \(x_i^*\) es simplemente un punto dentro del intervalo \([x_{i-1},x_i]\). Cuando el límite anterior existe se dice que la función \(f(x)\) es integrable.

Además, en el caso de que \(F(x)\) sea una primitiva de la función \(f(x)\), es decir, \(F'(x)=f(x)\), es bien conocido que la integral definida puede calcularse como:

\[\int_a^b f(x)dx = F(b)-F(a)\]

Este tipo de integrales pueden calcularse con ayuda Python. En concreto, el paquete de cálculo simbólico (SymPy) dispone de la función integrate que puede ser utilizada tanto para el cálculo de la integral indefinida (primitivas) como definida.

---

Ejemplo:

La integral \(\int_{\pi/2}^\pi\left(\frac{1}{x^2}-3x+2\cos(x)\right)dx\) se calcula de la siguiente manera:

En primer lugar, se necesitaría importar el correspondiente paquete

import sympy as sp

Despues se definiría una variable simbólica y a partir de ella la expresión simbólica de la función a integrar

x = sp.Symbol('x')
f = 1/x**2 - 3*x + 2*sp.cos(x)

Si se desea calcular la integral indefinida, bastaría con indicar en el comando integrate la expresión simbólica de la función y la variable de integración

sp.integrate(f, x)

\[\displaystyle - \frac{3 x^{2}}{2} + 2 \sin{\left(x \right)} - \frac{1}{x}\]

El resultado anterior es la expresión simbólica de una primitiva. Debe recordarse que la integral indefinida implicaría añadir una constante de integración arbitraria.

La integral definida puede calcularse de dos maneras, evaluando la primitiva anterior en los extremos del intervalo o usando directamente el comando integrate pero señalando los límites de la variable

sp.integrate(f, (x, sp.pi/2, sp.pi))

\[\displaystyle - \frac{9 \pi^{2}}{8} - 2 + \frac{1}{\pi}\]

Si se desea una aproximación numérica de esa expresión exacta, se podría utilizar el método evalf aplicado sobre el resultado anterior

sp.integrate(f, (x, sp.pi/2, sp.pi)).evalf()

\[\displaystyle -12.7849950650417\]

Se puede comprobar cómo efectivamente ese valor coincide con la diferencia del valor de la primitiva en los extremos del intervalo. En este caso se utiliza la función subs del paquete SymPy para sustituir valores en expresiones.

primitiva = sp.integrate(f, x)
primitiva.subs(x,sp.pi) - primitiva.subs(x,sp.pi/2)

\[\displaystyle - \frac{9 \pi^{2}}{8} - 2 + \frac{1}{\pi}\]

En el caso de funciones positivas ya se sabe que la integral definida se interpreta como el área que queda comprendida por debajo de la gráfica de la función y encima del eje de abcisas entre los dos extremos del intervalo.

Python dispone además de funcionalidades que permiten realizar representaciones gráficas de funciones. Precisamente usando el paquete Matplotlib se puede comprobar cómo efectivamente las sumas de Riemann van aproximado el valor de ese área.

---

Ejemplo:

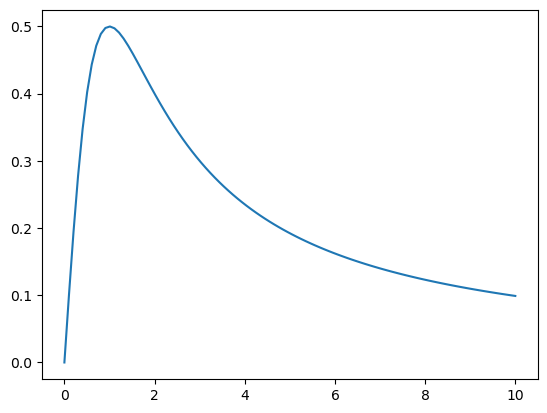
Se desea calcular

\[\int_0^{10}\frac{x}{x^2+1}dx\]

para ello se comienza por definir la función y hacer una representación gráfica de la misma en el intervalo \([0,10]\). Esta representación puede hacerse con el módulo pyplot del paquete Matplotlib. Además, para hacer la representación se necesita definir una partición de ese intervalo mediante la función linspace del paquete Numpy.

import numpy as np
import matplotlib.pyplot as plt
f = lambda x : x/(x**2+1)
x = np.linspace(0, 10, num=100)
plt.plot(x, f(x))
plt.show()

El área que queda comprendida por debajo de la curva puede calcularse con la integral definida

x = sp.Symbol('x')
sp.integrate(x/(x**2+1), (x,0,10))

\[\displaystyle \frac{\log{\left(101 \right)}}{2}\]

cuyo valor numérico es

integral = sp.integrate(x/(x**2+1), (x,0,10)).evalf()
integral

\[\displaystyle 2.30756025842063\]

Ese área puede aproximarse calculando las sumas de Riemann, tal como puede comprobarse con el siguiente código. El código comienza solicitando el número de subintervalos para la división del intervalo \([0,10]\). Para elegir un punto en cada intervalo se pueden usar diferentes estrategias, por ejemplo elegir uno de los extremos de cada subintervalo, pero también elegir el punto medio. Esta última será la estrategia utilizada para aproximar la integral mediante las sumas de Riemann.

n = int(input('Número de subintervalos:'))
a, b = 0, 10
x = np.linspace(a,b,num=100)
y = f(x)
particion = np.linspace(a,b,num=n+1)
puntosMedios = (particion[:-1] + particion[1:])/2 
y_med = f(puntosMedios)
plt.plot(x, y, 'b')
plt.plot(puntosMedios, y_med, 'b.', markersize=10)
plt.bar(puntosMedios, y_med, width=(b-a)/n, alpha=0.25, edgecolor='b')
plt.title('Sumas de Riemann con ' + str(n) + ' subintervalos')
iaprox = sum(y_med*(b-a)/n)
print('Valor aproximado de la integral:', iaprox)

Valor aproximado de la integral: 2.3597256258496997

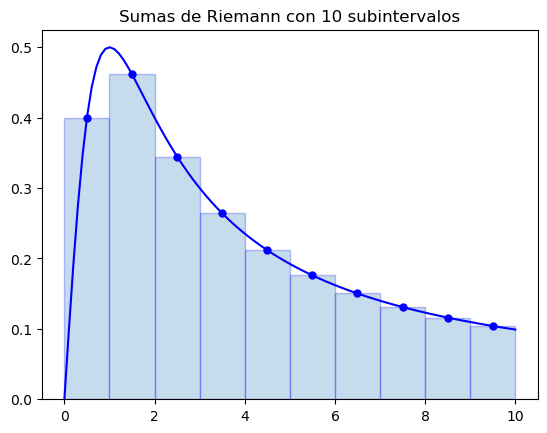
Se puede comprobar cómo a medida que aumenta el número de subintervalos la aproximación de la integral es de mejor calidad.

a, b = 0, 10
print('VALOR EXACTO:', integral)
for n in range(5,80,5):
    particion = np.linspace(a,b,num=n+1)
    puntosMedios = (particion[:-1] + particion[1:])/2 
    y_med = f(puntosMedios)
    iaprox = sum(y_med*(b-a)/n)
    print(f'Valor aproximado con {n} subintervalos: {iaprox:.4f}')

VALOR EXACTO: 2.30756025842063
Valor aproximado con 5 subintervalos: 2.4841
Valor aproximado con 10 subintervalos: 2.3597
Valor aproximado con 15 subintervalos: 2.3282
Valor aproximado con 20 subintervalos: 2.3186
Valor aproximado con 25 subintervalos: 2.3145
Valor aproximado con 30 subintervalos: 2.3123
Valor aproximado con 35 subintervalos: 2.3110
Valor aproximado con 40 subintervalos: 2.3102
Valor aproximado con 45 subintervalos: 2.3097
Valor aproximado con 50 subintervalos: 2.3093
Valor aproximado con 55 subintervalos: 2.3090
Valor aproximado con 60 subintervalos: 2.3087
Valor aproximado con 65 subintervalos: 2.3086
Valor aproximado con 70 subintervalos: 2.3084
Valor aproximado con 75 subintervalos: 2.3083

---

Determinadas funciones, o bien no aceptan primitivas o bien su cálculo es demasiado complejo. En tales casos se puede recurrir a métodos numéricos de aproximación de las correspondientes integrales.

En Python existe un paquete, el paquete SciPy, que entre otras muchas cosas implementa métodos numéricos de integración.

---

Ejemplo:

Considérese la integral

\[\int_\pi^{2\pi}cos(e^{1/x})dx\]

En primer lugar es fácil comprobar que la función integrate no es capaz de encontrar una expresión analítica de la integral:

x = sp.Symbol('x')
sp.integrate(sp.cos(sp.exp(1/x)), (x,0,10))

\[\displaystyle \int\limits_{0}^{10} \cos{\left(e^{\frac{1}{x}} \right)}\, dx\]

En casos como estos no queda más remedio que recurrir a algún método numérico de aproximación de la integral. Para ello el paquete SciPy dispone de una librería scipy.integrate en la que se implementan diferentes métodos numéricos de integración, tanto para integrales en una variable como para integrales dobles o triples. En el caso de funciones de una variable, la integración se realiza con la función quad. Otras funciones disponibles son:

• quad: integración simple

• dblquad: integración doble

• tplquad: integración triple

• nquad: integración múltiple

• trapz: integración con la regla del trapecio

• simps: regla de Simpson

• polyint: integración analítica de polinomios

Dependiendo de la plataforma que se esté utilizando, es posible que se requiera una instalación previa de este paquete. Esto puede realizarse directamente con la instrucción !pip install scipy.

Asumiendo que el paquete se encuentra instalado, lo siguiente que debe hacerse es importar el módulo de integración:

from scipy import integrate

La integración numérica no puede realizarse sobre expresiones simbólicas, por lo que es necesario definir las funciones a integrar como expresiones funcionales conocidas como “expresiones lambda”. También es posible utilizar la instrucción def() para definir las funciones, pero de necesitar funciones matemáticas básicas se tendrían que usar las del paquete Numpy y no las del paquete SymPy.

A continuación se define la función \(cos(e^{1/x})\) cuya integral no puede obtenerse con métodos analíticos exactos

f = lambda x: np.cos(np.exp(1/x))

Para el cálculo numérico de una integral simple se usa la función quad() que recibe tres argumentos: la función y los dos límites de integración.

integrate.quad(f, np.pi, 2*np.pi)

(0.9947169317864027, 1.1043576406537556e-14)

La función devuelve dos valores, el primero es el valor aproximado de la integral y el segundo una estimación del error absoluto cometido con la aproximación.

A la hora de calcular integrales es posible incluso definir límites de integración infinitos.

integrate.quad(lambda x : np.exp(-x**2), 0, np.inf)

(0.8862269254527579, 7.101318390472462e-09)

Concepto de integral doble

Consideremos una función real de dos variables reales \(f:D\subseteq R^2\rightarrow R\) donde \(D\) es un cierto dominio cerrado de \(R^2\), una primera pregunta que puede surgir es tratar de entender el significado de calcular la integral de la función \(f\) sobre el dominio \(D\), para posteriormente tratar de identificar posibles aplicaciones prácticas de este concepto.

Teniendo presente el caso de una variable, el objetivo es generalizar ese concepto para funciones \(f(x,y)\) de dos variables. En primer lugar, una función \(f(x,y)\) determina una superficie en el espacio tridimensional \(z=f(x,y)\), por lo que podría tener sentido tratar de calcular el volumen del sólido que dicha superficie encierra por encima de una cierta región \(D\) en el dominio de la función.

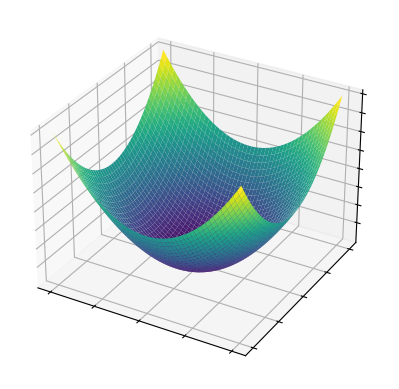
La representación gráfica de funciones de dos variables también puede hacerse con el paquete Matplotlib. Por ejemplo, a continuación se muestra la representación gráfica de la función \(f(x,y)=x^2+y^2+1\) sobre la región \(D=[-10,10]\times[-10,10]\) que se encuentra dentro de su dominio.

import matplotlib.pyplot as plt
x, y = np.meshgrid(np.linspace(-10, 10), np.linspace(-10, 10))
z = x**2 + y**2 + 1
fig, ax = plt.subplots(subplot_kw={"projection": "3d"})
ax.plot_surface(x, y, z, vmin=z.min()*2, cmap='viridis')
ax.set(xticklabels=[], yticklabels=[], zticklabels=[])
plt.show()

La integración doble de una función de dos variables consiste en calcular el volumen que queda comprendido por debajo de la superficie de la función y por encima de un determinado dominio de integración \(\Omega\) en el plano OXY.

En general dada una función \(f:D\subseteq R^2\rightarrow R\) y una región en el plano \(\Omega\subseteq D\), la integral

\[\iint\limits_\Omega f(x,y)dA\]

se define en la siguiente manera:

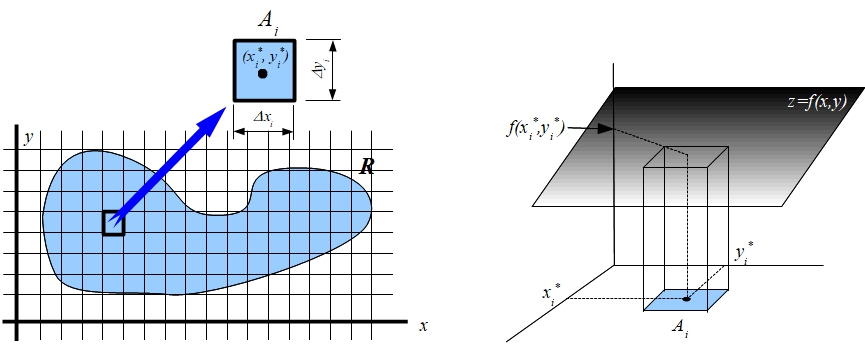
• Se divide la región \(\Omega\) de forma arbitraria en una serie de dominios parciales \(A_1,A_2,\dots,A_n\) de áreas respectivas \(\Delta A_1,\Delta A_2,\dots,\Delta A_n\).

• Se considera un punto arbitrario \((x_i^*,y_i^*)\in A_i\) para \(i=1,2,\dots,n\).

• Se calcula una aproximación del volumen mediante la fórmula

  \[ \sum_{i=1}^n f(x_i^*,y_i^*)\Delta A_i\]

• Se define la integral doble como el límite de la expresión anterior cuando las áreas de los subdominios tienden a cero, para ello se considera \(\Delta A=\max\{\Delta A_1,\Delta A_2,\dots,\Delta A_n\}\) y

\[\iint\limits_\Omega f(x,y)dA = \lim_{\Delta A\rightarrow 0}\sum_{i=1}^n f(x_i^*,y_i^*)\Delta A_i\]

En la notación utilizada anteriormente \(dA\) representa un diferencial de área, que habitualmente se expresa como \(dx\,dy\), al tomarse subdominios \(A_i\) rectangulares. Estos subdominios rectangulares pueden generarse a partir de sendas subdivisiones realizadas sobre los ejes \(OX\) y \(OY\). Cada uno de los subdominios determina un volumen de los que aparecen en el sumatorio de la expresión anterior.

Por supuesto, el límite anterior no siempre existe o converge hacia un valor finito, de manera que conviene definir el concepto de función integrable en la forma siguiente:

Función integrable:

Una función \(f(x,y)\) es integrable sobre una región \(\Omega\) cuando el siguiente límite existe y tiende a un valor finito

\[\lim_{\Delta A\rightarrow 0}\sum_{i=1}^n f(x_i^*,y_i^*)\Delta A_i\]

Una primera pregunta que puede surgir es si existe alguna condición sobre la función que garantice su integrabilidad. A continuación se presentan tres casos en los que se puede garantizar:

• Toda función continua sobre un dominio \(\Omega\) es integrable en dicho dominio.

• Si \(f(x,y)\) está acotada en \(\Omega\) y tiene en dicho dominio un número finito de puntos de discontinuidad la función es integrable en \(\Omega\).

• Si \(f(x,y)\) está acotada en \(\Omega\) y tiene en dicho dominio un número infinito de puntos de discontinuidad distribuidos sobre un número finito de arcos rectificables de curvas planas contenidas en \(\Omega\), la función es integrable en \(\Omega\).

Por ejemplo, las funciones

\[\begin{split}f(x,y)=\left\{ \begin{array}{ll} x+y & \mbox{si }(x,y)\neq (0,0) \\ 1 & \mbox{si }(x,y) = (0,0) \end{array} \right. \;\;\; g(x,y)=\left\{ \begin{array}{ll} x+y & \mbox{si }x<1 \\ 1 & \mbox{si }x\geq 1 \end{array} \right.\end{split}\]

son integrables a pesar de tener puntos de discontinuidad. La funcion \(f(x,y)\) presenta un único punto de discontinuidad en el \((0,0)\), lo que no impide que sea integrable sobre cualquier región de integración \(\Omega\subset R^2\). La función \(g(x,y)\) tiene infinitos puntos de discontinuidad, pero todos ellos están sobre la recta \(x=1\). A pesar de esos puntos de discontinuidad, la función sigue siendo integrable.

En Python sería fácilmente implementable un procedimiento que calcule la aproximación de la integral doble mediante la generalización del concepto de sumas de Riemann a una función de dos variables. Por ejemplo, asumiendo que el dominio de integración es rectangular del tipo \([x_{min},x_{max}]\times[y_{min},y_{max}]\), se podría hacer una subdivisión de los dos intervalos y calcular la suma de los volúmenes de las barras cuya base es cada uno de los subrectángulos y la altura el valor de la función en la esquina inferior izquierda de ese subrectángulo. Eso es precisamente lo que se realiza con el siguiente código para aproximar la integral de la función \(f(x,y)=5-x^2-y^2\) en el dominio \([-1,1]\times[-1,1]\)

# Función y dominio de integración
def f(x, y): return 5 - x**2 - y**2
xmin, xmax = -1, 1
ymin, ymax = -1, 1

Con ayuda del paquete SymPy se podría calcular el valor exacto de la integral, ya que la instrucción integrate() que se utilizó para integrales en una variable, también puede ser utiizada para calcular integrales múltiples. En este caso debe advertirse que para declarar en una sola instrucción dos variables simbólicas, debe usarse la función symbols() y no Symbol().

x,y = sp.symbols('x,y')
sp.integrate(5-x**2-y**2, (x,-1,1), (y,-1,1))

\[\displaystyle \frac{52}{3}\]

sp.integrate(5-x**2-y**2, (x,-1,1), (y,-1,1)).evalf()

\[\displaystyle 17.3333333333333\]

A continuación se define una función que calcula las sumas de Riemann haciendo una subdivisión de los intervalos de variación de la \(x\) y de la \(y\) en \(n\) subintervalos. Posteriormente se hace un bucle para comprobar cómo al aumentar el valor de \(n\) esas sumas de Riemann se van acercando al valor de la integral.

def sumasRiemann(f, xmin, xmax, ymin, ymax, n):
    delta_x, delta_y = (xmax-xmin)/n,  (ymax-ymin)/n
    suma = 0.0
    for i in range(n):
        for j in range(n):
            x_ij = xmin + i * delta_x
            y_ij = ymin + j * delta_y
            # acumula volumen barra
            suma += delta_x * delta_y * f(x_ij, y_ij)
    return suma

for n in range(2,41,2):
    v = sumasRiemann(f, xmin, xmax, ymin, ymax, n)
    print(f'Suma de Riemann para n={n}: {v:.4f}')

Suma de Riemann para n=2: 16.0000
Suma de Riemann para n=4: 17.0000
Suma de Riemann para n=6: 17.1852
Suma de Riemann para n=8: 17.2500
Suma de Riemann para n=10: 17.2800
Suma de Riemann para n=12: 17.2963
Suma de Riemann para n=14: 17.3061
Suma de Riemann para n=16: 17.3125
Suma de Riemann para n=18: 17.3169
Suma de Riemann para n=20: 17.3200
Suma de Riemann para n=22: 17.3223
Suma de Riemann para n=24: 17.3241
Suma de Riemann para n=26: 17.3254
Suma de Riemann para n=28: 17.3265
Suma de Riemann para n=30: 17.3274
Suma de Riemann para n=32: 17.3281
Suma de Riemann para n=34: 17.3287
Suma de Riemann para n=36: 17.3292
Suma de Riemann para n=38: 17.3296
Suma de Riemann para n=40: 17.3300

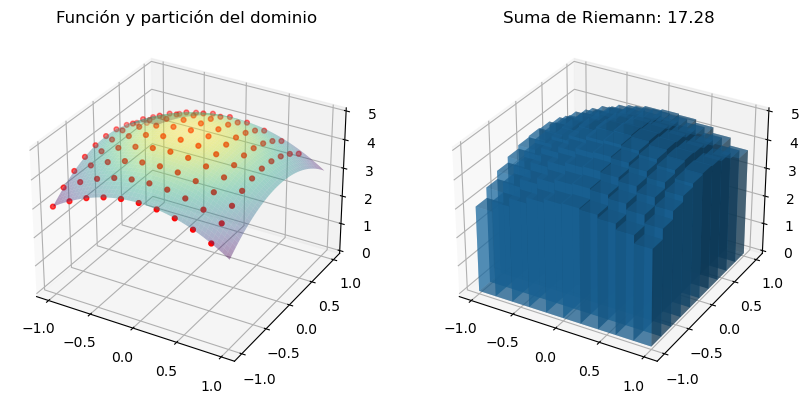
Incluso, gracias a las prestaciones gráficas del paquete Matplotlib, puede visualizarse el proceso de aproximación del volumen bajo la superficie con los volúmenes de una serie de barras verticales sobre los subrectángulos de la división del dominio.

import numpy as np
import matplotlib.pyplot as plt

# Número de subdivisiones en los intervalos de x e y
n = 10
dx, dy = (xmax-xmin)/n, (ymax-ymin)/n

# Aproximación del volumen con las sumas de Riemann
volumen = sumasRiemann(f, xmin, xmax, ymin, ymax, n)

# Partición para las sumas de Riemann
xp, yp = np.meshgrid(np.linspace(xmin, xmax-dx, n), np.linspace(ymin, ymax-dy, n))
zp = f(xp, yp)
# partición para representar la superficie
xs, ys = np.meshgrid(np.linspace(xmin, xmax), np.linspace(ymin, ymax))
zs = f(xs, ys)

fig, ax = plt.subplots(nrows=1, ncols=2, figsize=(10, 8), subplot_kw={"projection": "3d"})
# superficie de la función
ax[0].set_title('Función y partición del dominio')
ax[0].set_zlim(0, 5)
ax[0].plot_surface(xs, ys, zs, cmap='viridis', alpha=0.4)
ax[0].scatter(xp, yp, zp, color='red', s=12)

# Altura de las barras de la suma de Riemann
dz = zp.flatten()
# Coordenadas de inicio de las barras
x_bars = xp.flatten()
y_bars = yp.flatten()
z_bars = np.zeros_like(dz)

ax[1].set_title(f'Suma de Riemann: {volumen:.2f}')
ax[1].bar3d(x_bars, y_bars, z_bars, dx, dy, dz, alpha=0.5, shade=True)
plt.show()

Propiedades de las funciones integrables

Algunas propiedades básicas de las funciones integrables son:

• Dada una región \(\Omega\subseteq R^2\) el área de dicha región es \(Area=\iint\limits_\Omega dA\).

• Si \(f(x,y)\) y \(g(x,y)\) son dos funciones integrables sobre \(\Omega\) y \(a,b\in R\) entonces

\[\iint\limits_\Omega(a\,f(x,y)+b\,g(x,y))dA=a\iint\limits_\Omega f(x,y)dA+b\iint_{\Omega}g(x,y)dA\]

• Si \(f(x,y)\) es integrable sobre una región \(\Omega\) que puede descomponerse como unión de dos regiones \(D_1\) y \(D_2\) con ningún punto interior común, entonces

\[\iint\limits_\Omega f(x,y)dA=\iint\limits_{D_1}f(x,y)dA+\iint\limits_{D_2}f(x,y)dA\]

• Si \(f(x,y)\) es integrable sobre \(\Omega\), también lo es \(|f(x,y)|\), verificándose además

\[\left|\iint\limits_\Omega f(x,y)dA\right|\leq\iint\limits_{\Omega}|f(x,y)|dA\]

Al respecto de esta última propiedad conviene puntualizar que, al igual que ocurre en el caso de la integración de funciones de una variable, si la función toma valores negativos sobre un dominio, su integral también será negativa. Dicho de otra manera, los volúmenes que quedan determinados por debajo del plano \(OXY\) se consideran negativos. Esto tiene su efecto a la hora de calcular volúmenes de sólidos determinados por superficies de funciones que en unos puntos toman valores positivos y en otros negativos, ya que si se hace una integración directa unos volúmenes se cancelarían con otros, por lo que debe descomponerse la región de integración en subregiones dependiendo de los signos que toma la función en ellas.

Cálculo de integrales dobles

Una vez entendido el concepto de integral doble, se necesita disponer de métodos efectivos de cálculo. Como se analizará a continuación, el cálculo de una integral doble puede reducirse al cálculo de dos integrales simples de manera iterada.

Para entender el procedimiento de cálculo se tomará como ejemplo el cálculo de la integral

\[\iint\limits_R(x^2+y^2+1)dA\]

siendo \(R=[-1,1]\times[-1,1]\). La representación gráfica de esa función se generó anteriormente y lo que se trata ahora es de calcular el volumen del sólido que determina esa superficie por encima del dominio.

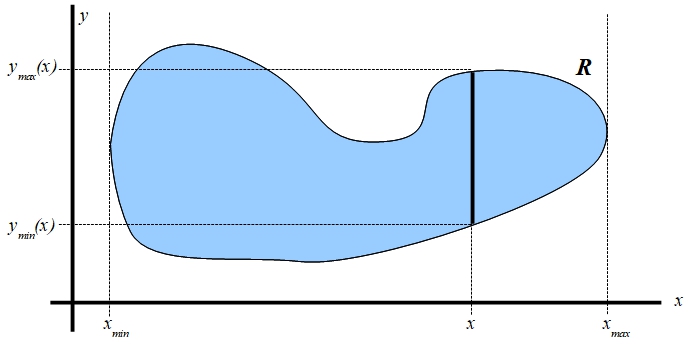
La región de integración es un conjunto acotado, en el que el valor de la variable \(x\) se mantiene dentro de unos límites \(x\in[x_{min},x_{max}]\); en este caso concreto \(x_{min}=-1\) y \(x_{max}=1\). Fijado un valor de \(x\), el valor de la variable \(y\) podría variar a su vez dentro de un intervalo que en principio puede depender del valor de \(x\): \(y\in[y_{min}(x),y_{max}(x)]\). En este primer ejemplo, realmente los valores de \(y_{min}\) e \(y_{max}\) no dependen de \(x\), siendo \(y_{min}=-1\) e \(y_{max}=1\), pero en general podría ocurrir que sí que dependieran del valor de \(x\), tal como se muestra en la siguiente figura, que viene a representar una posible región de integración más compleja.

Fijado el valor de \(x\), se podría calcular la integral

\[S(x)=\int_{y_{min}(x)}^{y_{max}(x)}f(x,y)dy\]

representando esta integral el área de la superficie que queda por debajo de la gráfica de la función y en el plano determinado por el valor de \(x\), tal como muestra la figura siguiente

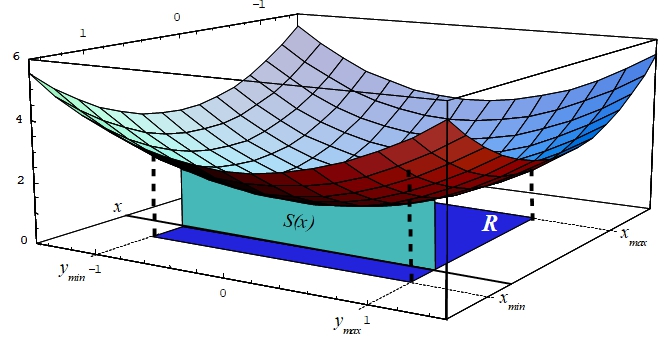
El área \(S(x)\) dentro del sólido tridimensional genera un volumen \(S(x)dx\), donde el diferencial de \(x\) viene a representar el “grosor” del corte que se genera por debajo de la superficie entre \(y_{min}\) e \(y_{max}\).

El volumen que define la integral doble podría verse entonces como la suma de los infinitos volúmenes de la forma \(S(x)dx\). En definitiva:

\[Volumen =\int_{x_{min}}^{x_{max}}S(x)dx\]

obteniéndose finalmente

\[\iint\limits_R f(x,y)dA =\int_{x_{min}}^{x_{max}}\left(\int_{y_{min}(x)}^{y_{max}(x)}f(x,y)dy\right)dx\]

Por supuesto, se podría haber empezado fijando el valor de \(y\) y calculando las áreas \(S(y)\) generadas por cortes transversales. En este caso el intervalo de variación de la \(x\) podría depender del valor de \(y\), y se obtendría una forma equivalente de calcular la integral:

\[\iint\limits_R f(x,y)dA =\int_{y_{min}}^{y_{max}}\left(\int_{x_{min}(y)}^{x_{max}(y)}f(x,y)dx\right)dy\]

Ambas expresiones de la integral doble son equivalentes a los efectos de calcular su valor, y se conocen como integrales iteradas.

Como primer ejemplo de cálculo de la integral doble, se calculan ambas integrales iteradas sobre el ejemplo que se ha venido considerando.

---

Ejemplo:

Dada la función \(f(x,y)=x^2+y^2+1\) y el dominio de integración \(R=[-1,1]\times[-1,1]\). Para calcular

\[\iint\limits_R (x^2+y^2+1)dA =\int_{-1}^{1}\left(\int_{-1}^{1}(x^2+y^2+1)dy\right)dx\]

se empieza realizando la integral interior:

\[\int_{-1}^{1}(x^2+y^2+1)dy = \left. x^2y+\frac{y^3}{3}+y\right|_{y=-1}^{y=1}= \left(x^2+\frac{1}{3}+1\right)-\left(-x^2-\frac{1}{3}-1\right)=2x^2+\frac{8}{3}\]

para posteriormente realizar la integral exterior:

\[\int_{-1}^{1}\left(2x^2+\frac{8}{3}\right)dx = \left. \frac{2x^3}{3}+\frac{8}{3}x\right|_{x=-1}^{x=1}= \left(\frac{2}{3}+\frac{8}{3}\right)-\left(-\frac{2}{3}-\frac{8}{3}\right)=\frac{20}{3}\]

Se comprueba a continuación que cambiando el orden de realización de las integrales iteradas el resultado sigue siendo el mismo.

Para calcular

\[\iint\limits_R (x^2+y^2+1)dA =\int_{-1}^{1}\left(\int_{-1}^{1}(x^2+y^2+1)dx\right)dy\]

se empieza realizando la integral interior:

\[\int_{-1}^{1}(x^2+y^2+1)dx = \left. \frac{x^3}{3}+xy^2+x\right|_{x=-1}^{x=1}= \left(\frac{1}{3}+y^2+1\right)-\left(-\frac{1}{3}-y^2-1\right)=2y^2+\frac{8}{3}\]

para posteriormente realizar la integral exterior:

\[\int_{-1}^{1}\left(2y^2+\frac{8}{3}\right)dy = \left. \frac{2y^3}{3}+\frac{8}{3}y\right|_{y=-1}^{y=1}= \left(\frac{2}{3}+\frac{8}{3}\right)-\left(-\frac{2}{3}-\frac{8}{3}\right)=\frac{20}{3}\]

Como puede apreciarse, de las dos formas se obtiene el mismo resultado.

Esta integral, por supuesto, también puede ser calculada mediante la función de integración simbólica de Python.

Para calcular integrales del tipo

\[\int_a^b\left(\int_c^df(x,y)dx\right)dy\]

de forma simbólica se tendría que utilizar la sintaxis integrate(f,(x,c,d),(y,a,b))

Por ejemplo, la integral

\[\iint\limits_R (x^2+y^2+1)dA =\int_{-1}^{1}\left(\int_{-1}^{1}(x^2+y^2+1)dx\right)dy\]

se calcularía de la siguiente manera:

import sympy as sp
x,y = sp.symbols('x,y')
F = x**2 + y**2 +1
sp.integrate(F, (x, -1, 1), (y, -1, 1))

\[\displaystyle \frac{20}{3}\]

Calculadas las integrales iteradas en el orden inverso, se obtiene, obviamente, el mismo resultado

sp.integrate(F, (y, -1, 1), (x, -1, 1))

\[\displaystyle \frac{20}{3}\]

---

Ejemplo:

Se presenta a continuación un nuevo ejemplo en el que la región de integración resulta un poco más compleja.

Se desea calcular la integral doble de la función \(f(x,y)=2x^3-xy^2+5xy\) sobre el recinto triangular \(T\) determinado por los puntos \((0,0)\), \((0,3)\) y \((2,2)\).

Con el paquete Matplotlib de Python también es posible obtener una representación de regiones poligonales como la que se plantea:

from matplotlib.patches import Polygon
import matplotlib.pyplot as plt
R = Polygon([(0,0), (0,3), (2,2)])
fig, ax = plt.subplots()
ax.add_patch(R)
plt.ylim(0,3); plt.xlim(0,3);

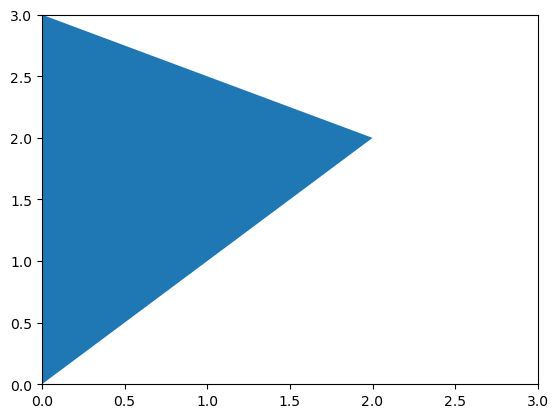
Para calcular esa integral lo primero que debe hacerse es parametrizar el recinto de integración. Tal como se ve a continuación:

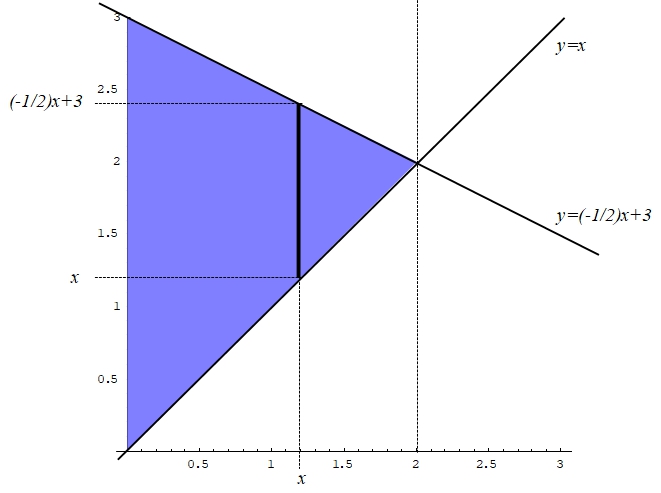
Tomando un valor de \(x\) entre 0 y 2, el valor de la \(y\) variaría entre \(x\) y \(-\frac{x}{2}+3\). Por tanto

\[\iint\limits_T (2x^3-xy^2+5xy)dA =\int_{0}^{2}\left(\int_{x}^{-\frac{x}{2}+3}(2x^3-xy^2+5xy)dy\right)dx\]

En primer lugar debe realizarse la integral interior:

\[\int_{x}^{-\frac{x}{2}+3}(2x^3-xy^2+5xy)dy= \left. 2x^3y-x\frac{y^3}{3}+5x\frac{y^2}{2} \right|_{y=x}^{y=-\frac{x}{2}+3}= -\frac{3}{8}(7x^4-9x^3+8x^2-36x)\]

Posteriormente se realiza la integral exterior:

\[\int_{0}^{2} -\frac{3}{8}(7x^4-9x^3+8x^2-36x) dx = \frac{157}{10}\]

De nuevo se puede comprobar la corrección del proceso realizado calculando la integral con ayuda de Python

x,y = sp.symbols('x,y')
F = 2*x**3 - x*y**2 + 5*x*y
sp.integrate(F, (y, x, -x/2+3), (x, 0, 2))

\[\displaystyle \frac{157}{10}\]

---

Ejemplo:

A efectos prácticos, evidentemente únicamente es necesario realizar una de las integrales iteradas, aunque conviene elegir cuidadosamente el orden de integración más apropiado en función de las características del recinto de integración. Por ejemplo, las siguientes dos integrales iteradas son equivalentes, sin embargo la integración de la segunda es mucho más simple. Se puede comprobar que su valor es \(e-2\).

\[\int_{0}^{1}\left(\int_{x}^{\sqrt{x}}\frac{e^y}{y}dy\right)dx=\int_{0}^{1}\left(\int_{y^2}^{y}\frac{e^y}{y}dx\right)dy= e-2\]

x,y = sp.symbols('x,y')
F = sp.exp(y)/y
sp.integrate(F, (x, y**2, y), (y, 0, 1))

\[\displaystyle -2 + e\]

---

Al igual que ocurría en la integración simple, existen integrales dobles que no pueden calcularse de manera analítica y se necesita recurrir a la integración numérica (aproximación del valor de la integral). La función de integración doble numérica del paquete SciPy es dblquad. A continuación se muestra un ejemplo

---

Ejemplo:

La integración simbólica de la siguiente integral no es posible

\[\iint_{[0,1]\times[0,1]}y^xe^{-x^2}dxdy\]

x,y = sp.symbols('x,y')
F = y**x*sp.exp(-x**2)
sp.integrate(F, (x, 0, 1), (y, 0, 1))

\[\displaystyle \int\limits_{0}^{1} \int\limits_{0}^{1} y^{x} e^{- x^{2}}\, dx\, dy\]

Para el cálculo de aproximaciones de integrales dobles puede usarse la función dblquad(F, a, b, g, h) que obtendría el valor de la siguiente integral:

\[\int_a^b\left(\int_{g(x)}^{h(x)}F(y,x)dy\right)dx\]

Debe observarse que el orden en el que se definen los argumentos de la función \(F(y,x)\) es diferente al habitual, por lo que se podría hacer un intercambio de los papeles de las variables \(x\) e \(y\) para obtener la siguiente integral equivalente

\[\int_{y=a}^{y=b}\left(\int_{x=g(y)}^{x=h(y)}f(x,y)dx\right)dy\]

En cualquiera de los casos, se debe tener especial cuidado, ya que los límites de integración de la primera variable son los que pueden depender de la segunda, mientras que los límites de integración de la segunda variable deben ser constantes. En el caso de que sea al revés, podría intercambiarse el papel de las variables en la definición de la función.

Las funciones \(g\) y \(h\) de la integral interior y la función a integrar \(f\) deben ser definidas mediante sendas expresiones lambda o la sentencia def.

En la integral \(\iint_{[0,1]\times[0,1]}y^xe^{-x^2}dxdy\), al ser los límites de integración constantes, solo se necesita definir como función el integrando.

g = lambda x,y : y**x*np.exp(-x**2)
integrate.dblquad(g, 0, 1, 0, 1)

(0.5442561925461458, 5.075310172131253e-10)

---

Obviamente, en recintos de integración que no sean de tipo rectangular, el cálculo de la integral doble requiere una correcta identificación de los límites de las variables, para lo cual puede ser interesante realizar representaciones gráficas de las funciones que delimitan el recinto de integración. Además la elección correcta del orden de las integrales iteradas puede simplificar el proceso de cálculo.

---

Ejemplo:

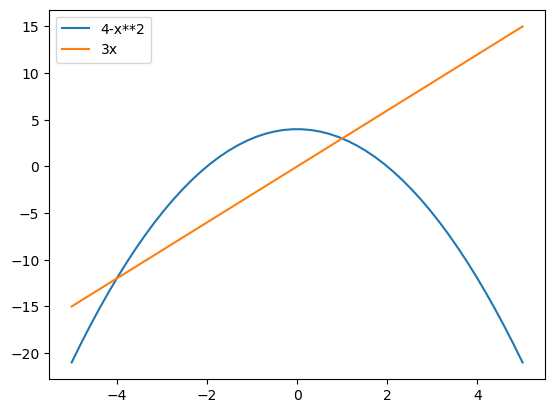
Calcular \(\iint\limits_D x^2dA\) donde \(D\) es el dominio delimitado por las curvas \(y=4-x^2\) e \(y=3x\).

Para el cálculo de dicha integral es preciso identificar bien los límites de integración. Una representación gráfica de las dos curvas que delimitan el recinto puede servir como primera aproximación:

x = np.linspace(-5,5,50)
plt.plot(x, 4-x**2, label='4-x**2')
plt.plot(x, 3*x, label='3x')
plt.legend()
plt.show()

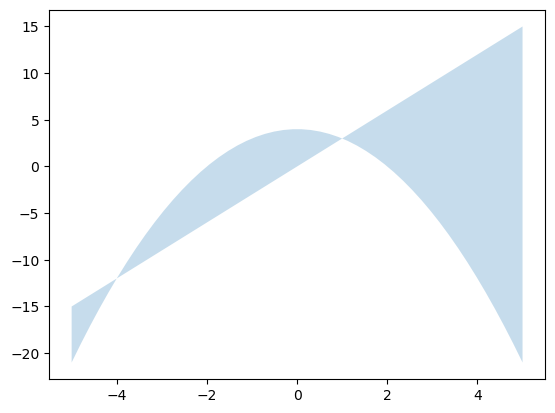
Matplotlib dispone también de una función que representa el área entre dos curvas.

x = np.linspace(-5,5,50)
fig, ax = plt.subplots()
ax.fill_between(x, y1 = 4-x**2, y2 = 3*x, alpha = 0.25)

<matplotlib.collections.PolyCollection at 0x271d2f13c10>

Los dos puntos de corte entre las dos curvas que delimitan el recinto pueden calcularse mediante la resolución de la ecuación algebraica \(4-x^2=3x\). SymPy incorpora la función solve() para obtener soluciones de ecuaciones (se asume que la ecuación está igualada a 0).

x = sp.Symbol('x')
sp.solve(4-x**2-3*x, x)

[-4, 1]

Una vez identificados los puntos, la integral se podría realizar mediante las siguientes integrales iteradas:

\[\int_{-4}^1\left(\int_{3x}^{4-x^2}x^2dy\right)dx\]

Esa integral doble puede calcularse tanto de forma simbólica como numérica:

x,y = sp.symbols('x,y')
sp.integrate(x**2, (y, 3*x, 4-x**2), (x, -4, 1))

\[\displaystyle \frac{875}{12}\]

sp.integrate(x**2, (y, 3*x, 4-x**2), (x, -4, 1)).evalf()

\[\displaystyle 72.9166666666667\]

Para calcular numéricamente la integral con el módulo de integración del paquete SciPy debe tenerse en cuenta que en la integral

\[\int_{-4}^1\left(\int_{3x}^{4-x^2}x^2dy\right)dx\]

la variable cuyos límites de integración dependen de la otra es la variable \(y\), por lo tanto, el papel de ambas debería cambiarse (\(x\rightarrow y, y\rightarrow x\)) y considerar la integral

\[\int_{-4}^1\left(\int_{3y}^{4-y^2}y^2dx\right)dy\]

y por tanto, el cálculo de la integral con la función dblquad() se realizaría de la siguiente manera:

integrate.dblquad(lambda x,y:y**2, -4, 1, lambda y:3*y, lambda y:4-y**2)

(72.91666666666666, 8.095376221225099e-13)

---

Como ya se comentado, el orden de la realización de las integrales iteradas puede influir en el esfuerzo de cálculo que se requiera para realizar las integrales iteradas, o incluso la necesidad de hacer subsivisiones en el recinto de integración. El siguiente ejemplo pone esto de manifiesto.

---

Ejemplo:

Considérese la integral

\[\iint_D(x+y)dxdy\]

donde \(D\) es el recinto que viene determinado por las rectas \(2x-y=1\) y \(x+3y=4\) y los ejes coordenados. El recinto puede visualizarse fácilmente, para lo que una opción es usar las posibilidades de representación de ecuaciones implícitas que incorpora el paquete SymPy

x,y = sp.symbols('x,y')
e1 = sp.Eq(2*x-y,1)
e2 = sp.Eq(x+3*y,4)
r1 = sp.plot_implicit(e1, (x, 0, 5), (y, 0, 2), line_color='red', show=False)
r2 = sp.plot_implicit(e2, (x, 0, 5), (y, 0, 2), line_color='blue', show=False)
r1.append(r2[0])
r1.show()

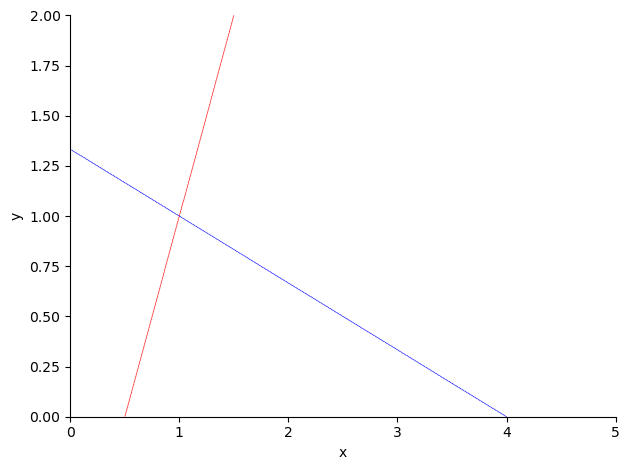
A la vista del recinto triangular delimitado, parece necesario identificar las coordenadas de los tres vértices. Python ofrece opciones de resolución de ecuaciones que pueden ser utilizadas

sp.solve([2*x-y-1, y], x, y)

{x: 1/2, y: 0}

sp.solve([2*x-y-1, x+3*y-4], x, y)

{x: 1, y: 1}

sp.solve([y, x+3*y-4], x, y)

{x: 4, y: 0}

Teniendo en cuenta esos vértices y la forma del recinto de integración, la integral doble tendría que desdoblarse en dos si se desea definir en primer lugar los límites de la variable \(x\)

\[\int_{1/2}^1\left(\int_{0}^{2x-1}(x+y)dy\right)dx + \int_{1}^{4}\left(\int_{0}^{(4-x)/3}(x+y)dy\right)dx\]

x,y = sp.symbols('x,y')
sp.integrate(x+y, (y, 0, 2*x-1), (x, 1/2, 1)) + sp.integrate(x+y, (y, 0, (4-x)/3), (x, 1, 4))

\[\displaystyle 3.79166666666667\]

En cambio, si se opta por empezar determinando los límites de la variable \(y\), se necesitaría calcular una única integral doble

\[\int_{0}^1\left(\int_{(y+1)/2}^{4-3y}(x+y)dx\right)dy\]

x,y = sp.symbols('x,y')
sp.integrate(x+y, (x, (y+1)/2, 4-3*y), (y, 0, 1)).evalf()

\[\displaystyle 3.79166666666667\]

Ejercicios propuestos

• Calcular \(\iint\limits_D (y^2-2xy)dA\) siendo \(D=[0,2]\times[0,1]\).

• Calcular \(\iint\limits_D x^2dA\) donde \(D\) es el dominio delimitado por las curvas \(y=4-x^2\) e \(y=3x\).

• Calcular \(\iint\limits_D (x^2-y)dA\) donde \(D\) es la región del primer cuadrante delimitada por los ejes y la recta \(2x+y=4\).

• Usar la integración doble para calcular el área de la región encerrada por las curvas \(x-y=2\) e \(y=-x^2\).

• Calcular el volumen del sólido que forma en el primer octante del espacio la superficie \(z=4-x^2-y\).