Métodos numéricos de resolución de ecuaciones diferenciales

No toda ecuación diferencial puede resolverse de manera analítica simbólica. Además en muchas ocasiones resulta imposible encontrar definiciones explícitas de las funciones solución.

En tales casos no queda más remedio que utilizar algún método numérico que al menos trate de aproximar las soluciones de los problemas de valor inicial en un cierto intervalo próximo al punto que determina la condición inicial.

Existe una gran variedad de métodos numéricos, algunos de los más conocidos corresponden a la familia de métodos de Runge-Kutta. Realmente hay diferentes versiones de ese método, pero el más habitual es el método de Runge-Kutta de cuarto orden, que permite aproximar soluciones con un pequeño margen de error y además es fácilmente implementable.

La versión más simple del método de Runge-Kutta, también conocido como método de Euler, se aplica a la resolución de problemas de valor inicial del tipo

\[\begin{split}\left\{ \begin{array}{l} \frac{dy}{dt}=f(t,y)\\ y(t_0)=y_0 \end{array} \right. \end{split}\]

y se basa en, partiendo de \(y_0=y(t_0)\), construir las aproximaciones \(y_{n+1}=y(t_{n+1})\) de la siguiente forma

\[y_{n+1}=y_n+h\,f(t_n,y_n)\]

donde \(h=t_{n+1}-t_n\) es el tamaño del paso en una partición del intervalo en el que se quiere aproximar la solución.

Debe tenerse en cuenta que \(f(t_n,y_n)\), de acuerdo a la ecuación diferencial, sería \(\frac{dy}{dt}(t_n)\), es decir, la pendiente de la recta tangente a la función solución en \(t=t_n\).

\[\frac{y_{n+1}-y_{n}}{h}\approx f(t_n,y_n)\]

Las distintas variantes del método de Runge-Kutta sustituyen el valor de esa pendiente por un promedio de otras pendientes. El orden del método determina el número de términos utilizados para calcular ese promedio. Uno de los métodos más usados es precisamente el de orden cuatro.

Método de Runge-Kutta de cuarto orden

Dado el problema de valor inicial

\[\begin{split}\left\{ \begin{array}{l} \frac{dy}{dt}=f(t,y)\\ y(t_0)=y_0 \end{array} \right. \end{split}\]

para empezar se debe elegir un tamaño de paso \(h\) y un número máximo de iteraciones \(N\), de forma que se van construyendo de forma iterativa los puntos:

\[y_{n+1}=y_n+\frac{h}{6}(k_1+2k_2+2k_3+k_4)\]

para \(n=1,2,\dots,N-1\). En cada iteración los valores de las constantes \(k_i\) se calculan de la siguiente manera:

\[\begin{split}\begin{array}{l} k_{1} = f(t_n,y_n)\\ k_{2} = f(t_n+\frac{h}{2},y_n+\frac{k_1}{2})\\ k_{3} = f(t_n+\frac{h}{2},y_n+\frac{k_2}{2})\\ k_{4} = f(t_n+h,y_n+k_3) \end{array}\end{split}\]

De esta forma la solución se construye a lo largo del intervalo \([t_0, t_0+hN]\). Los valores \(y_n\) corresponderían a las aproximaciones de la solución en los puntos \(t_n=t_0+nh\).

En el método el valor \(y_{n+1}\) se obtiene a partir del valor del punto previo \(y_n\) y el producto del tamaño del intervalo (\(h\)) por una estimación de la pendiente de la solución en el punto. Esa pendiente estimada se calcula como un promedio ponderado de varias pendientes:

• \(k_1\) es la pendiente al principio del intervalo.

• \(k_2\) es la pendiente en el punto medio del intervalo, usando \(k_1\) para determinar el valor de \(y\) en el punto \(t_n + h/2\).

• \(k_3\) es de nuevo la pendiente del punto medio, pero ahora usando \(k_2\) para determinar el valor de \(y\).

• \(k_4\) es la pendiente al final del intervalo, con el valor de \(y\) determinado por \(k_3\)

En el promedio ponderado se asigna mayor peso a las pendientes en el punto medio.

Como se ha comentado existe un amplio abanico de variantes de este método básico, pero el de Runge-Kutta de orden 4 es uno de los más utilizados.

Resolución numérica de ecuaciones con Python

Entre los paquetes disponibles en Python se encuentra el paquete de cálculo científico SciPy. Dicho paquete implementa diferentes “solvers” que se pueden aplicar a la resolución numérica de problemas de valor inicial. https://docs.scipy.org/doc/scipy/reference/integrate.html

Dentro del módulo de integración (integrate) del paquete SciPy existen una serie de rutinas que implementan diferentes métodos para la resolucion de problemas de valor inicial. La más general es solve_ivp() que permite señalar el método a utilizar a través de un parametro opcional method. https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.solve_ivp.html

La función solve_ivp() resuelve problemas de valor inicial del tipo

\[\begin{split}\left\{ \begin{array}{l} \frac{dy}{dt}=f(t,y)\\ y(t_0)=y_0 \end{array} \right. \end{split}\]

Los tres argumentos obligatorios que debe recibir solve_ivp() son:

• Función \(f(t,y)\), debe ser una función numérica ejecutable. Puede ser generada por una expresión lambda o a partir de una expresión simbólica usando la función lambdify de SymPy

• Intervalo de integración \((t_0,t_f)\) donde se quiere aproximar la solución del problema. Debe darse como una secuencia de dos valores entre corchetes: [t0,tf]

• Valor \(y_0\). Al permitir la resolución también de sistemas de ecuaciones, este tercer argumento debe ser un array con los valores iniciales de todas las funciones. En el caso de una única ecuación, el valor debe ser dado entre corchetes: [y0]

Entre los argumentos opcionales, hay tres especialmente importantes:

• El cuarto argumento, t_eval es un array con los valores de la variable \(t\) en los que se quiere conocer el valor de la función solución. En caso de no proporcionar ese array, el propio método usa los extremos del intervalo de integración y puntos intermedios elegidos en función del método utilizado.

• El parámetro opcional method determina el método a utilizar, estando disponibles diferentes versiones del método de Runge-Kutta. La opción por defecto (method='RK45') usa el método Runge-Kutta de orden 5 para determinar los pasos, controlando la precisión con el método de orden 4.

• El parámetro dense_output es una variable booleana que indica si lo que se quiere es calcular una función continua

La función solve_ivp() devuelve un objeto que contiene diferentes campos con información sobre el proceso de resolución y la solución obtenida. La información más importante sería:

• t: array con los valores de la variable \(t\).

• t: array con los valores estimados de la función solución \(y\) para los respectivos valores de \(t\).

• sol: función con la estimación de la solución en el caso de que el parámetro dense_output hubiese sido establecido como True.

• nfev: número de evaluaciones realizadas de la función \(f(t,y)\).

• success: variable boolean indicando si el proceso a finalizado con éxito

A continuación se muestran algunos ejemplos de la resolución numérica de problemas de valor inicial.

---

Ejemplo:

Como primer ejemplo se considera el problema de valor inicial:

\[\begin{split}\left\{ \begin{array}{l} \frac{dy}{dt}=t+y^2\\ y(0)=1 \end{array} \right. \end{split}\]

Aparentemente es un problema sencillo, pero la obtención de una expresión simbólica de la función resulta imposible con las funciones que ofrece el paquete SymPy.

import sympy as sp

try:
    t = sp.Symbol('t')
    y = sp.Function('y')
    edo = sp.Eq(y(t).diff(t), t + y(t)**2)
    condicion = {y(0):1}
    sp.dsolve(edo, ics=condicion)
except Exception:
    print('No puedo resolver la ecuación')

No puedo resolver la ecuación

La alternativa de resolución numérica pasa por recurrir a la función solve_ivp() que ofrece el paquete de cálculo científico SciPy. Esta función permitirá aproximar la solución del problema en puntos posteriores al estado inicial correspondiente a \(t_0=0\). Por ejemplo, podríamos desear conocer el valor de la función solución en el punto \(t_f=0.5\), es decir, aproximar \(y(0.5)\).

Para hacerlo es preciso definir una función numérica \(f(t,y)\). Eso puede hacerse directamente con la definición de expresiones lambda en Python

fn = lambda t,y: t+y**2

Una alternativa podría ser convertir en función numérica ejecutable una expresión simbólica con la instrucción lambdify de SymPy. Por ejemplo:

t = sp.Symbol('t')
y = sp.Function('y')
f = t + y(t)**2
fn2 = sp.lambdify((t, y(t)), f)

El siguiente paso es definir el intervalo determinado por el valor de la variable independiente en el estado inicial (\(t_0\)) y en el correspondiente al estado final que se desea aproximar (\(t_f\)).

En el ejemplo, como el punto inicial corresponde a \(t_0=0\), se puede considerar el siguiente intervalo:

t0, y0 = 0, 1
tf = 0.5
intervalo = [t0, tf]

Una vez que se tienen todos los elementos, lo único que se necesita es importar la función solve_ivp() del módulo de integración de SciPy y hacer la llamada correspondiente. En este caso se va a solicitar al algorimto que aproxime también la solución en una serie de puntos intermedios del intervalo de integración. Estos puntos se incluyen con el parámetro t_eval.

from scipy.integrate import solve_ivp
solve_ivp(fn, intervalo, [y0], t_eval=[0, 0.1, 0.2, 0.3, 0.4, 0.5])

  message: 'The solver successfully reached the end of the integration interval.'
     nfev: 14
     njev: 0
      nlu: 0
      sol: None
   status: 0
  success: True
        t: array([0. , 0.1, 0.2, 0.3, 0.4, 0.5])
 t_events: None
        y: array([[1.        , 1.11667844, 1.275828  , 1.48831434, 1.78733335,
        2.23475388]])
 y_events: None

Como puede observarse, solve_ivp() devuelve varios elementos de información, los más importantes son:

• success señala si el algoritmo pudo completarse con éxito

• t vector de valores de la variable independiente en el intervalo de integración

• y vector con los valores de la solución correspondientes a los respectivos valores de la variable independiente (t)

solucion = solve_ivp(fn, intervalo, [y0], t_eval=[0, 0.1, 0.2, 0.3, 0.4, 0.5])

solucion.success

True

solucion.t

array([0. , 0.1, 0.2, 0.3, 0.4, 0.5])

solucion.y

array([[1.        , 1.11667844, 1.275828  , 1.48831434, 1.78733335,
        2.23475388]])

Si lo que se desea es obtener una representación de la función solución en un determinado intervalo, puede usarse la opción de generar una salida densa a modo de función continua (dense_output=True)

solucion = solve_ivp(fn, intervalo, [y0], dense_output=True)

En este caso, además de obtener la información obtenida anteriormente, el algoritmo devuelve una función de nombre sol que puede ser utilizada para evaluar la función solución en cualquier punto

solucion.sol([0.25])

array([[1.37400135]])

import numpy as np
solucion.sol(np.linspace(0,1,10))

array([[ 1.        ,  1.13211608,  1.31771775,  1.57590733,  1.96314656,
         2.5795993 ,  3.56913155,  5.11931142,  7.46140919, 10.87039723]])

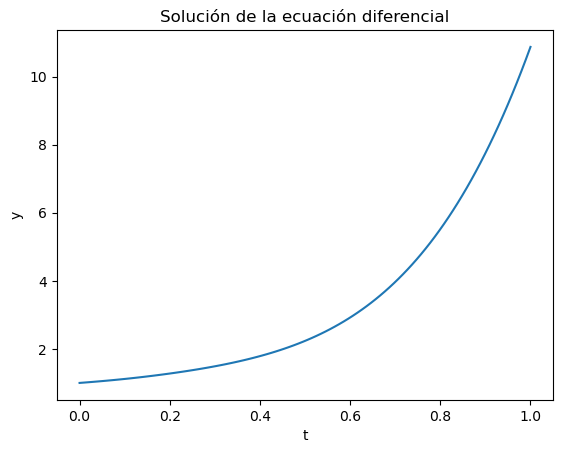
Gracias a la definición de una función solución, se podría realizar una representación gráfica de la misma.

import matplotlib.pyplot as plt
import numpy as np
t = np.linspace(0,1,100)
y = solucion.sol(t).T
plt.plot(t, y)
plt.xlabel('t'); plt.ylabel('y')
plt.title('Solución de la ecuación diferencial')
plt.show()

---

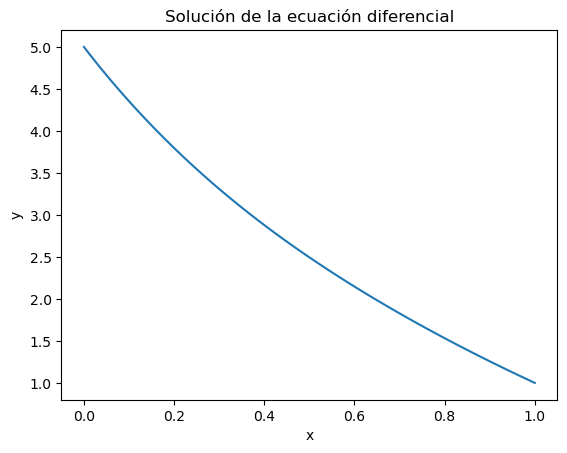
Ejemplo:

Al presentar las ecuaciones exactas se comprobó que la siguiente ecuación no puede ser resuelta por Python en modo simbólico.

\[(2xy+y^2)dx+(x^2+2xy-6)dy=0 \Rightarrow \frac{dy}{dx}=-\frac{2xy+y^2}{x^2+2xy-6}\]

Se muestra a continuación cómo obtener una aproximación de la solución que cumple la condición inicial \(y(1)=5\).

fn = lambda x,y: -(2*x*y+y**2)/(x**2+2*x*y-6)
t0, y0 = 1, 5
intervalo = [1,2]
solucion = solve_ivp(fn, intervalo, [y0], dense_output=True)

print(solucion.success)
print(solucion.t)
print(solucion.y)

True
[1.         1.0841449  1.85815192 2.        ]
[[5.         4.45017067 1.37571649 1.00616587]]

x = np.linspace(1,2,100)
y = solucion.sol(x).T
plt.plot(t, y)
plt.xlabel('x'); plt.ylabel('y')
plt.title('Solución de la ecuación diferencial')
plt.show()

---

Ejemplo:

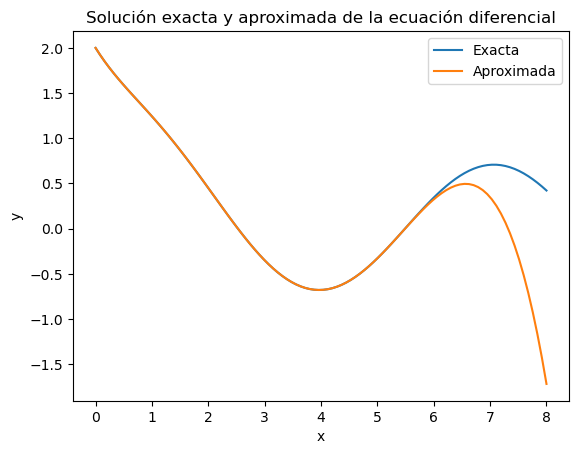
Para poder tener una visión sobre la calidad de la solución aproximada numéricamente puede ser interesante compararla con la solución exacta en el caso de problemas que pueden resolverse simbólicamente. Se considera en este ejemplo el problema de valor inicial:

\[\begin{split}\left\{ \begin{array}{l} \frac{dy}{dt}= -y +\cos t\\ y(0)=2 \end{array} \right. \end{split}\]

La solución exacta es:

t = sp.Symbol('t')
y = sp.Function('y')
edo = sp.Eq(y(t).diff(t), -y(t) + sp.cos(t))
condicion = {y(0):2}
sp.dsolve(edo, ics=condicion)

\[\displaystyle y{\left(t \right)} = \frac{\sin{\left(t \right)}}{2} + \frac{\cos{\left(t \right)}}{2} + \frac{3 e^{- t}}{2}\]

Se puede generar una versión numérica de la función extrayendo la parte de la derecha de la expresión que define la solución (rhs) y usar la instrucción lambdify()

sp.dsolve(edo, ics=condicion).rhs

\[\displaystyle \frac{\sin{\left(t \right)}}{2} + \frac{\cos{\left(t \right)}}{2} + \frac{3 e^{- t}}{2}\]

solexacta = sp.lambdify(t, sp.dsolve(edo, ics=condicion).rhs)

Se procede a continuación a la obtención de la aproximación numérica de la solución en el intervalo \([0,5]\)

fn = lambda t,y: -y + np.cos(t)
t0 = 0
y0 = 2
intervalo = [0,5]
solnumerica = solve_ivp(fn, intervalo, [y0], dense_output=True)

t = np.linspace(0,8,100)
ye = solexacta(t)
yn = solnumerica.sol(t).T
plt.plot(t, ye, label='Exacta')
plt.plot(t, yn, label='Aproximada')
plt.xlabel('x'); plt.ylabel('y')
plt.title('Solución exacta y aproximada de la ecuación diferencial')
plt.legend()
plt.show()