Integral de línea de campos vectoriales

Un campo de vectorial puede verse como un campo de fuerzas que indica la fuerza que se aplica sobre una partícula en función de su posición en el plano o en el espacio. Por otro lado, una curva determina la trayectoria de movimiento de esa partícula, de manera que podría tener sentido tratar de evaluar el trabajo total que realiza el campo sobre la partícula a lo largo de la trayectoria, o dicho de otra forma, la energía necesaria para desplazar la partícula en su trayectoria. Esta es precisamente la interpretación física del concepto de integral de línea de un campo vectorial.

---

Ejemplo:

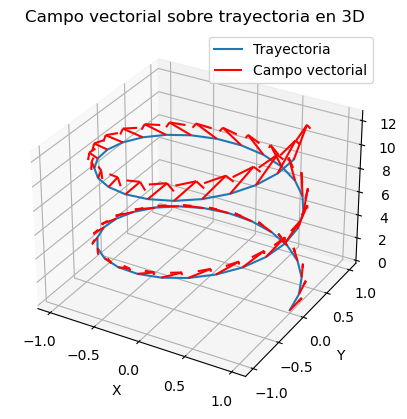
Con el siguiente código Python puede obtenerse una visualización del efecto del campo \(\vec{F}(x,y,z)=-0.2x\vec{i}+0.25y\vec{j}+0.15z\vec{k}\) sobre una partícula que se desplaza siguiendo una trayectoria helicoidal \(\vec{r}(t)=(\cos t, \sin t, t)\) con \(t\in[0,4\pi]\):

import numpy as np
import matplotlib.pyplot as plt

# Trayectoria
t = np.linspace(0, 4*np.pi, 50)
x, y, z = np.cos(t), np.sin(t), t

# Campo vectorial
cx, cy, cz = -0.2*y, 0.25*x, 0.15*z

# Grafica la trayectoria y los vectores del campo vectorial
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_xlabel('x'); ax.set_ylabel('y');

ax.plot(x, y, z, label='Trayectoria')
ax.quiver(x, y, z, cx, cy, cz, color='red', label='Campo vectorial')

ax.set_title('Campo vectorial sobre trayectoria en 3D')
ax.set_xlabel('X'); ax.set_ylabel('Y')
ax.legend()
plt.show()

---

Si la partícula \(P\) recorre una cierta trayectoria \(\vec{r}(t)\) y sobre cada punto de la trayectoria el campo aplica una fuerza \(\vec{F}(\vec{r}(t))\) el trabajo que en un punto concreto realiza el campo es:

\[Trabajo = Fuerza \circ Desplazamiento = \vec{F}\circ\Delta\vec{r}\]

El desplazamiento total entre dos posiciones a lo largo de una curva \(C\) puede considerarse como el resultado de sumar infinitos desplazamientos elementales y el trabajo total realizado por la fuerza en ese desplazamiento será la suma de todos esos trabajos elementales; es decir, en términos de integración, el trabajo total vendría dado por

\[Trabajo=\int_C \vec{F}\circ d\vec{r}= \lim_{\Delta\vec{r}_i\rightarrow 0} \sum_i \vec{F}_i\circ \Delta\vec{r}_i\]

Si se tiene en cuenta que \(\Delta\vec{r}_i\) puede ser expresado en términos del vector velocidad:

\[\Delta\vec{r}_i = \frac{\Delta\vec{r}_i}{\Delta t}\Delta t\]

entonces

\[\lim_{\Delta\vec{r}_i\rightarrow 0} \sum_i \vec{F}_i\circ \Delta\vec{r}_i = \lim_{\Delta\vec{r}_i\rightarrow 0} \sum_i \vec{F}_i\circ \frac{\Delta\vec{r}_i}{\Delta t}\Delta t\]

y por tanto el trabajo puede medirse con la integral

\[Trabajo=\int_{t_1}^{t_2} \vec{F}\circ \frac{d\vec{r}}{dt}\,dt\]

Este es precisamente el concepto de integral curvilínea del campo \(\vec{F}\) a lo largo de una curva, concepto que se define formalmente a continuación.

Integral de línea de un campo vectorial:

Dado un campo vectorial \(\vec{F}\) y una curva \(C\) de clase \(C^1\) parametrizada por \(\vec{r}(t)\) con \(t\in[a,b]\), se define la integral de línea de \(\vec{F}\) sobre \(C\), también conocida como circulación de \(\vec{F}\) a lo largo de \(C\), como

\[\int_C \vec{F}\circ d\vec{r} = \int_{a}^{b} \vec{F}(\vec{r}(t))\circ \vec{r}\,'(t)\,dt\]

donde el operador \(\circ\) representa el producto escalar de vectores.

La integral anterior depende de la trayectoria \(C\) pero no de la parametrización equivalente que se elija, pero el signo de la integral sí que cambia al cambiar el sentido de recorrido sobre la curva. Debe tenerse en cuenta que la integral representa la energía necesaria para desplazar la partícula a lo largo de la curva, y como tal, su signo cambia al cambiar el sentido de recorrido.

A continuación se indica una notación alternativa que suele utilizarse para las integrales curvilíneas sobre campos vectoriales, tanto en el caso de campos y curvas en el plano como en el espacio.

Suponiendo que el campo \(\vec{F}\) viene dado por \(\vec{F}(x,y)=M(x,y)\vec{i}+N(x,y)\vec{j}\):

\[\int_C \vec{F}\circ d\vec{r} = \int_a^b \left(M(r_1(t),r_2(t)),N(r_1(t),r_2(t))\right) \circ\left(r_1'(t),r_2'(t)\right)dt \]

\[=\int_a^b \left(M(r_1(t),r_2(t))r_1'(t)+N(r_1(t),r_2(t))r_2'(t)\right)dt\]

lo que sugiere utilizar la notación

\[\int_C \vec{F}\circ d\vec{r} = \int_C M(x,y)dx+N(x,y)dy\]

De la misma forma, en el caso de un campo en el espacio \(\vec{F}(x,y,z)=P(x,y,z)\vec{i}+Q(x,y,z)\vec{j}+R(x,y,z)\vec{k}\), se podría utilizar la siguiente notación alternativa para definir la integral de línea o circulación:

\[\int_C \vec{F}\circ d\vec{r} = \int_C P(x,y,z)dx+Q(x,y,z)dy+R(x,y,z)dz\]

---

Ejemplo:

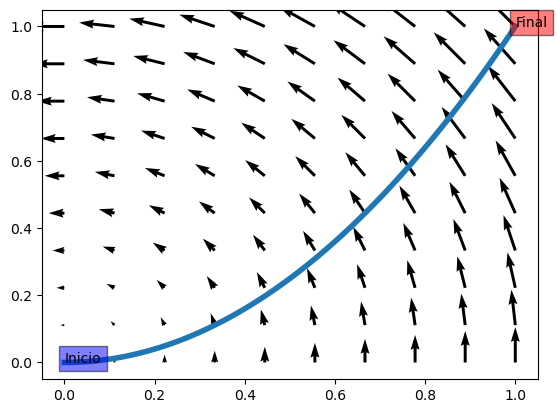
Considérese el campo vectorial \(\vec{F}(x,y)=-y\vec{i}+x\vec{j}\) y la curva \(C\) formada por la rama de la parábola \(y=x^2\) entre el punto \((0,0)\) y el punto \((1,1)\).

En primer lugar, se puede hacer una sencilla representación del campo y la trayectoria

x,y = np.meshgrid(np.linspace(0,1,10),np.linspace(0,1,10))
u, v = -y, x
plt.quiver(x,y,u,v)
t = np.linspace(0,1,100)
rx, ry = t, t**2
plt.plot(rx,ry, linewidth=4)
plt.text(rx[0], ry[0], 'Inicio', bbox=dict(facecolor='blue', alpha=0.5))
plt.text(rx[-1], ry[-1], 'Final', bbox=dict(facecolor='red', alpha=0.5))
plt.show()

Para calcular el trabajo total del campo sobre una partícula que se desplaza por esa trayectoria, se tendría que calcular la integral de línea o circulación del campo a lo largo de la curva.

Para poder calcular la integral de línea se necesita en primer lugar una parametrización de la curva. Una parametrización inmediata es:

\[\vec{r}(t)=(t,t^2)\;\mbox{ con }t\in[0,1]\]

de manera que \(\vec{r}\,'(t)=(1,2t)\), y por tanto

\[\int_C \vec{F}\circ d\vec{r} =\int_0^1(-t^2,t)\circ(1,2t)dt=\int_0^1 t^2dt = \frac{1}{3}\]

Utilizando la expresión alternativa de la integral de línea se obtiene, evidentemente, el mismo resultado:

\[\int_C -ydx+xdy = \int_0^1 -t^2dt+t2tdt=\int_0^1 t^2dt = \frac{1}{3}\]

Esa integral de línea podría calcularse con Python de varias maneras, tanto en modo simbólico como numérico. En el caso de la integración simbólica, se puede realizar con la función general de integración de SymPy o con la del módulo Vector.

import sympy as sp
import sympy.vector as vec
S = vec.CoordSys3D('')
t = sp.symbols('t')
x, y = t, t**2
Ft = -y*S.i + x*S.j
velocidad = sp.diff(x,t)*S.i + sp.diff(y,t)*S.j
sp.integrate(Ft.dot(velocidad), (t,0,1))

\[\displaystyle \frac{1}{3}\]

Con la función vector_integrate también podría calcularse la integral

from sympy.geometry import Curve
x,y,t = sp.symbols('x,y,t')
C = Curve((t,t**2), (t, 0, 1))
F = -S.y*S.i + S.x*S.j
vec.vector_integrate(F, C)

\[\displaystyle \frac{1}{3}\]

La integral de un campo vectorial depende de los valores del campo sobre los puntos de la curva, es decir, sobre la trayectoria, pero no de la parametrización que se elija de dicha curva. Así por ejemplo, la curva \(C\) podría haberse parametrizado de forma equivalente en la siguiente forma:

\[\vec{r}(t)=(\sin t,\sin^2 t)\;\mbox{ con }t\in[0,\pi/2]\]

En ese caso, la integral sería:

\[\int_C -ydx+xdy = \int_0^{\pi/2} -\sin^2 t\cos t\,dt + \sin t\,2\sin t\,\cos t\,dt\]

\[ = \int_0^{\pi/2} \sin^2 t\cos t\,dt =\left.\frac{\sin^3 t}{3} \right|_0^{\pi/2}=\frac{1}{3}\]

C = Curve((sp.sin(t), sp.sin(t)**2), (t, 0, sp.pi/2))
vec.vector_integrate(F, C)

\[\displaystyle \frac{1}{3}\]

---

Ejemplo:

Dado el campo vectorial \(\vec{F}(x,y)=xy\vec{i}+x^2\vec{j}\) y la curva \(C\) dada por

\[\vec{r}(t)=(3t-1,3t^2-2t)\;\mbox{ con }t\in[1,5/3]\]

la integral de línea sería:

\[\int_C xydx+x^2dy = \int_1^{5/3} (3t-1)(3t^2-2t)3dt + (3t-1)^2(6t-2)dt\]

\[ = \int_1^{5/3} (81t^3-81t^2+24t-2)dt=58\]

En Python podría calcularse de la siguiente manera:

F = S.x * S.y * S.i + S.x**2 * S.j
C = Curve((3*t-1, 3*t**2-2*t), (t, 1, 5/3))
vec.vector_integrate(F, C)

\[\displaystyle 58.0\]

---

Ejemplo:

Se desea calcular el trabajo ejercido por el campo \(\vec{F}(x,y,z)=(x^2+y^2+z^2)\vec{i}+z\vec{k}\) sobre una partícula que se desplaza por la hélice \(\vec{r}(t)=(\cos t, \sin t,t)\) con \(t\in[0,4\pi]\)

En este caso se trata de una curva en el espacio, pero el procedimiento para calcular el trabajo (integral de línea) es similar. En primer lugar, establecido el sistema de coordenadas, se debe definir la curva, su vector velocidad y el campo vectorial:

t = sp.symbols('t')
x, y, z = sp.cos(t), sp.sin(t), t
F = (x**2+y**2+z**2)*S.i + z*S.k
velocidad = sp.diff(x,t)*S.i + sp.diff(y,t)*S.j + sp.diff(z,t)*S.k
print('Vector velocidad:', velocidad)
print('Campo:',F)

Vector velocidad: (-sin(t))*.i + (cos(t))*.j + .k
Campo: (t**2 + sin(t)**2 + cos(t)**2)*.i + t*.k

La integral que debe realizarse es la correspondiente al producto escalar del campo por el vector velocidad

sp.integrate(F.dot(velocidad), (t,0,4*sp.pi))

\[\displaystyle 24 \pi^{2}\]

La otra alternativa para el cálculo de esta integral es de nuevo usar la función vector_integrate() del módulo Vector. En este caso la curva tridimensional debe definirse como un objeto de tipo ParametricRegion

c = vec.ParametricRegion((sp.cos(t),sp.sin(t),t), (t, 0, 4*sp.pi))
F = (S.x**2 + S.y**2 + S.z**2)*S.i + S.z*S.k
vec.vector_integrate(F, c)

\[\displaystyle 24 \pi^{2}\]

---

Ejemplo:

Se desea evaluar la integral \(\int_C(x^2+xy)dx+(x-2y)dy\) sobre el arco de la circunferencia \(x^2+y^2=4\) que va del punto \((2,0)\) al punto \((-2,0)\)

x,y = np.meshgrid(np.linspace(-2,2,10),np.linspace(-1,2,10))
u, v = x**2+x*y, x-2*y
plt.quiver(x,y,u,v)
plt.axis('equal')
t = np.linspace(0,np.pi)
rx, ry = 2*np.cos(t), 2*np.sin(t)
plt.plot(rx,ry, linewidth=4)
plt.text(rx[0], ry[0], 'Inicio', bbox=dict(facecolor='blue', alpha=0.5))
plt.text(rx[-1], ry[-1], 'Final', bbox=dict(facecolor='red', alpha=0.5))
plt.show()

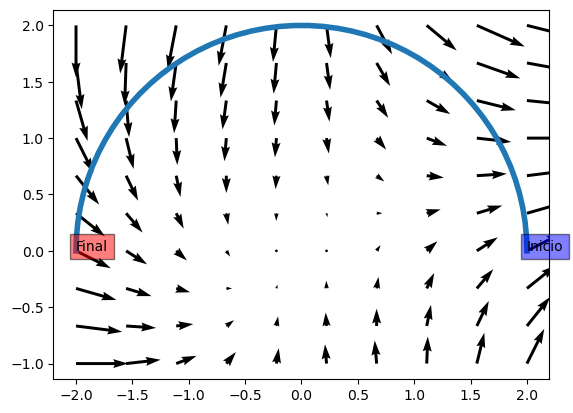
t = sp.symbols('t')
c = vec.ParametricRegion((2*sp.cos(t), 2*sp.sin(t)), (t, 0, sp.pi))
F = (S.x**2+S.x*S.y)*S.i + (S.x-2*S.y)*S.j
print('Trabajo:',vec.vector_integrate(F, c))

Trabajo: -16/3 + 2*pi

---

Por supuesto, el cálculo de integrales de línea también puede realizarse en el espacio tridimensional

---

Ejemplo:

Dado el campo vectorial \(\vec{F}(x,y) = xy\vec{i}+x^2\vec{j}+(x+y+z)\vec{k}\) y la curva C dada por \(\vec{r}(t)=(3t-1,3t^2-2t,t)\) con t \(\in [1,5]\).

# Campo vectorial
x,y,z = np.meshgrid(np.linspace(-1,1,6),np.linspace(-1,1,6),np.linspace(1,5,6))
u, v, w = x*y, x**2, x+y+z

# Trayectoria
t = np.linspace(1,5)
rx, ry, rz = np.cos(t), np.sin(t), t

# Grafica la trayectoria y los vectores del campo vectorial
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_xlabel('x'); ax.set_ylabel('y');

ax.plot(rx, ry, rz, label='Trayectoria')
ax.text(rx[0], ry[0], rz[0], 'Inicio', bbox=dict(facecolor='blue', alpha=0.5))
ax.text(rx[-1], ry[-1], rz[-1], 'Final', bbox=dict(facecolor='red', alpha=0.5))
ax.quiver(x, y, z, u, v, w, length=0.1, color='red', label='Campo vectorial')

ax.set_title('Campo vectorial sobre trayectoria en 3D')
ax.set_xlabel('X'); ax.set_ylabel('Y')
ax.legend()
plt.show()

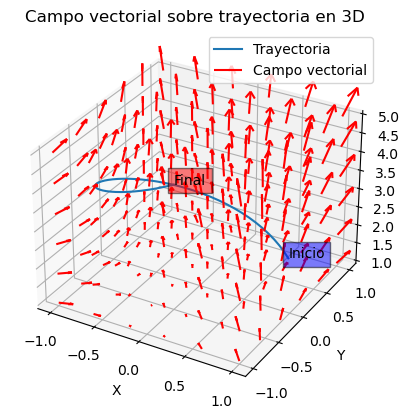
El trabajo que ejerce el campo, es decir, la integral de línea, se puede calcular de cualquiera de las dos formas siguientes:

t = sp.symbols('t')
x, y, z = 3*t-1, 3*t**2-2*t, t
F = x*y*S.i + x**2*S.j +(x+y+z)*S.k
velocidad = sp.diff(x,t)*S.i + sp.diff(y,t)*S.j + sp.diff(z,t)*S.k
sp.integrate(F.dot(velocidad), (t,1,5))

\[\displaystyle 9712\]

c = vec.ParametricRegion((3*t-1,3*t**2-2*t,t), (t, 1, 5))
F = S.x*S.y*S.i + S.x**2*S.j +(S.x+S.y+S.z)*S.k
vec.vector_integrate(F, c)

\[\displaystyle 9712\]

---

Ejemplo:

Se desea calcular el trabajo que ejerce el campo \(\vec{F}(x,y,z)=(x+y-z)\vec{i}+xyz\vec{j}+(x-z)\vec{k}\) sobre una partícula que se desplaza en línea recta entre el punto \((1,2,-1)\) y el punto \((2,0,5)\).

En primer lugar es necesario definir una parametrización del segmento que determina la trayectoria:

A = (1,2,-1)
B = (2,0,5)
c = vec.ParametricRegion((t*B[0] + (1-t)*A[0], t*B[1] + (1-t)*A[1], t*B[2] + (1-t)*A[2]), (t, 0, 1))
F = (S.x+S.y-S.z)*S.i + S.x*S.y*S.z*S.j +(S.x-S.z)*S.k
vec.vector_integrate(F, c)

\[\displaystyle - \frac{35}{6}\]

---

Aunque el valor absoluto de la integral de línea no depende de la parametrización de la curva, su signo sí que se ve influenciado por el recorrido de la curva.

Según cuál sea el sentido de recorrido, el campo puede oponerse o ayudar al movimiento.

• Si el campo se opone al momiviento, el valor de la integral será negativo, lo que indica que para desplazarse a lo largo de la trayectoria habrá que aplicar una energía igual al valor absoluto de la integral

• Si el campo ayuda al movimiento, el valor de la integral será positivo

En el siguiente sencillo ejemplo se puede comprobar con claridad.

---

Ejemplo:

Consideramos el campo uniforme \(\vec{F}=2\vec{i}+3\vec{j}\) y una partícula que se desplaza en línea recta entre el punto \(A=(1,1)\) y el punto \(B=(5,3)\). Si el desplazamiento es del punto \(A\) al \(B\), la trayectoria podría parametrizarse de la siguiente manera:

t = sp.symbols('t')
A = (1,1)
B = (5,3)
x = t*B[0] + (1-t)*A[0]
y = t*B[1] + (1-t)*A[1]
print(x)
print(y)

4*t + 1
2*t + 1

En este caso \(t\in[0,1]\), correspondiendo el valor \(t=0\) al punto \(A\) y \(t=1\) al punto \(B\).

Si se representa la trayectoria y el campo se observa que en este caso el campo favorece el desplazamiento, por lo que el signo de la integral será positivo

x,y = np.meshgrid(np.linspace(0,6,10),np.linspace(0,6,10))
u, v = 2, 3
plt.quiver(x,y,u,v)
t = np.linspace(0,1)
rx, ry = 4*t+1, 2*t+1
plt.plot(rx,ry, linewidth=4)
plt.text(rx[0], ry[0], 'Inicio', bbox=dict(facecolor='blue', alpha=0.5))
plt.text(rx[-1], ry[-1], 'Final', bbox=dict(facecolor='red', alpha=0.5))
plt.show()

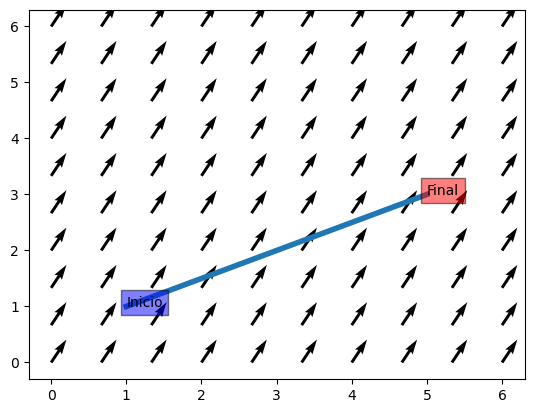
t = sp.symbols('t')
F = 2 * S.i + 3 * S.j
C = Curve((4*t+1, 2*t+1), (t, 0, 1))
vec.vector_integrate(F, C)

\[\displaystyle 14\]

A continuación, se analiza el caso en el que el recorrido de la trayectoria es en sentido contrario (de \(B\) hacia \(A\)). En este caso el campo se opone al movimiento, por lo que la integral será justamente la opuesta.

t = sp.symbols('t')
A = (1,1)
B = (5,3)
x = t*A[0] + (1-t)*B[0]
y = t*A[1] + (1-t)*B[1]
print(x)
print(y)

5 - 4*t
3 - 2*t

x,y = np.meshgrid(np.linspace(0,6,10),np.linspace(0,6,10))
u, v = 2, 3
plt.quiver(x,y,u,v)
t = np.linspace(0,1)
rx, ry = 5-4*t, 3-2*t
plt.plot(rx,ry, linewidth=4)
plt.text(rx[0], ry[0], 'Inicio', bbox=dict(facecolor='blue', alpha=0.5))
plt.text(rx[-1], ry[-1], 'Final', bbox=dict(facecolor='red', alpha=0.5))
plt.show()

t = sp.symbols('t')
F = 2 * S.i + 3 * S.j
C = Curve((5-4*t, 3-2*t), (t, 0, 1))
integral = vec.vector_integrate(F, C)
print('Valor de la integral de línea:', integral)

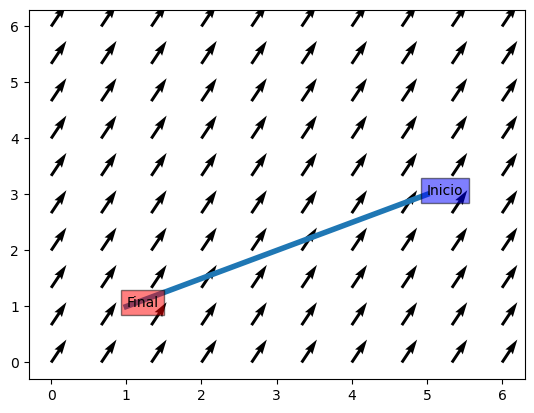
Valor de la integral de línea: -14

Otra opción más simple para definir trayectorias dadas por segmentos rectos es usar las funcionalidades de definición de segmentos y polígonos que tiene el paquete SymPy. En el caso de segmentos únicamente se tiene que señalar el punto de inicio y el de final

from sympy import Segment
A = (1,1)
B = (5,3)
F = 2 * S.i + 3 * S.j
segmento = Segment(A,B)
print('Integral de A a B:', vec.vector_integrate(F, segmento))
segmento2 = Segment(B,A)
print('Integral de B a A:', vec.vector_integrate(F, segmento2))

Integral de A a B: 14
Integral de B a A: -14

---

Ejemplo:

Se desea calcular el trabajo que ejerce el campo \(\vec{F}(x,y)=xy\vec{i}-2y\vec{j}\) sobre una partícula que parte del origen, para desplazarse siguiendo una poligonal a través de los puntos \((3,0)\), \((2,2)\) y \((1,5)\)

El trabajo se puede calcular sumando las integrales de línea correspondientes a cada uno de los tres segmentos de la trayectoria

F = S.x*S.y*S.i -2*S.y*S.j
F

\[\displaystyle (\mathbf{{x}_{}} \mathbf{{y}_{}})\mathbf{\hat{i}_{}} + (- 2 \mathbf{{y}_{}})\mathbf{\hat{j}_{}}\]

segmento1 = Segment((0,0), (3,0))
segmento2 = Segment((3,0), (2,2))
segmento3 = Segment((2,2), (1,5))
vec.vector_integrate(F, segmento1) + vec.vector_integrate(F, segmento2) + vec.vector_integrate(F, segmento3)

\[\displaystyle - \frac{97}{3}\]

---

Ejemplo:

En el caso de trayectorias poligonales cerradas, existe una alternativa más eficiente para calcular la integral de línea sobre la curva, se trata de considerar la definición del concepto de polígono. Por ejemplo, si en el caso del campo del ejemplo anterior, la trayectoria tuviese un segmento final que regresa al punto de partida \((0,0)\), el trabajo total se podría calcular de las siguientes dos formas alternativas:

F = S.x*S.y*S.i -2*S.y*S.j
tr1 = vec.vector_integrate(F, Segment((0,0),(3,0)))
tr2 = vec.vector_integrate(F, Segment((3,0),(2,2)))
tr3 = vec.vector_integrate(F, Segment((2,2),(1,5)))
tr4 = vec.vector_integrate(F, Segment((1,5),(0,0)))
tr1 + tr2 + tr3 + tr4

\[\displaystyle -9\]

from sympy.geometry import Polygon
F = S.x*S.y*S.i -2*S.y*S.j
trayectoria = Polygon((0,0), (3,0), (2,2), (1,5))
vec.vector_integrate(F, trayectoria)

\[\displaystyle -9\]

---

Otra característica importante de las integrales curvilíneas de campos vectoriales, y que puede ser comprobada con un simple análisis gráfico, es que su valor va a depender solo de la componente tangencial de \(\vec{F}\) sobre la curva, de manera que cuando las fuerzas del campo son perpendiculares a la curva en todos sus puntos, la integral resultará nula.

---

Ejemplo:

Dado el campo vectorial \(\vec{F}(x,y)=x\vec{i}+y\vec{j}\) y la curva \(C\) formada por la circunferencia de centro \((0,0)\) y radio 1, los vectores de campo en cada punto de la curva son ortogonales con la propia curva, tal como puede verse en la figura que se genera a continuación. Por tanto, la integral del campo sobre la curva será nula, por ser 0 el producto escalar entre \(\vec{F}(r_1(t),r_2(t))\) y \(\vec{r}\,'(t)\).

x,y = np.meshgrid(np.linspace(-1,1,10),np.linspace(-1,1,10))
u, v = x, y
plt.quiver(x,y,u,v)
t = np.linspace(0,2*np.pi)
rx, ry = np.cos(t), np.sin(t)
plt.plot(rx,ry, linewidth=4)
plt.axis('equal')
plt.show()

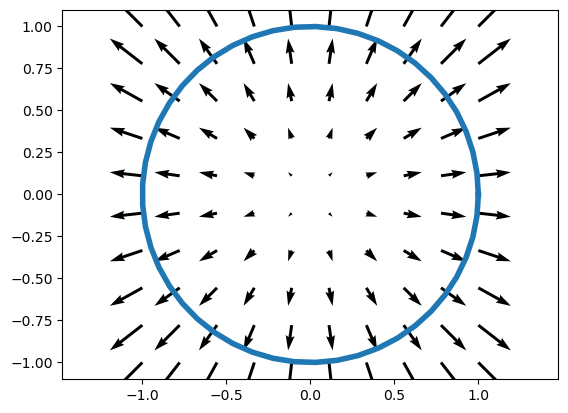
Para comprobar que la integral es nula se considerará la parametrización de \(C\):

\[\vec{r}(t)=(\cos t,\sin t)\;\mbox{ con }t\in[0,2\pi]\]

En un caso de curva cerrada como esta, se puede comprobar fácilmente que la integral de línea es independiente del punto a partir del cual se comienza a recorrer la curva. En este caso se está tomando como punto de partida para el recorrido el punto \((1,0)\).

El vector \(\vec{r}\,'(t)\) sería

\[\vec{r}\,'(t) = (-\sin t,\cos t)\]

y la integral resulta

\[\int_C xdx+ydy = \int_0^{2\pi} \cos t\,(-\sin t)dt +\sin t\,(\cos t)\,dt = \int_0^{2\pi} 0dt=0\]

Con Python pueden también verificarse los cálculos anteriores

t = sp.symbols('t')
F = S.x * S.i + S.y * S.j
C = Curve((sp.cos(t), sp.sin(t)), (t, 0, 2*sp.pi))
vec.vector_integrate(F, C)

\[\displaystyle 0\]

---

Ejemplo:

Comprobar el trabajo que ejercen los campos \(\vec{F}=\vec{i}+2\vec{j}\), \(\vec{G}=-2\vec{i}+\vec{j}\) y \(\vec{H}=-\vec{i}+\vec{j}\) sobre una partícula desplazándose en línea recta desde \((0,0)\) a \((1,1)\).

En primer lugar se va a hacer una representación gráfica de los tres escenarios que se proponen:

x,y = np.meshgrid(np.linspace(0,1,10),np.linspace(0,1,10))
t = np.linspace(0,1)
rx, ry = t, t
fig, ax = plt.subplots(nrows=1, ncols=3, sharey=True, figsize=(12, 3))
ax[0].set_title('Flujo del campo (1,2)')
ax[0].axis('equal')
ax[0].quiver(x,y,1,2)
ax[0].plot(rx,ry, linewidth=4)
ax[1].set_title('Flujo del campo (-2,1)')
ax[1].axis('equal')
ax[1].quiver(x,y,-2,1)
ax[1].plot(rx,ry, linewidth=4)
ax[2].set_title('Flujo del campo (-1,1)')
ax[2].axis('equal')
ax[2].quiver(x,y,-1,1)
ax[2].plot(rx,ry, linewidth=4)
plt.show()

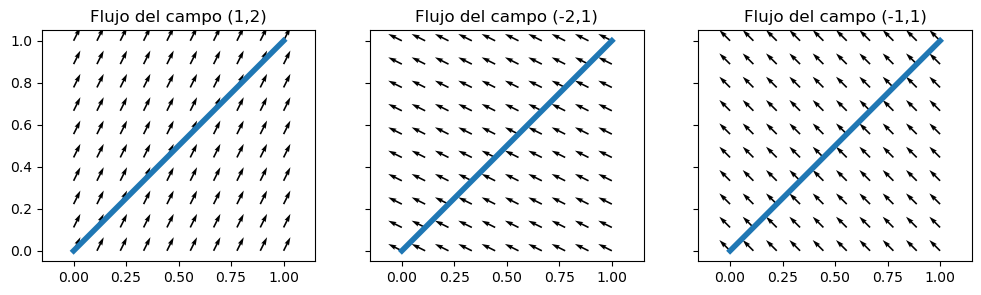
A la vista de los gráficos, se podría intuir que la integral de línea en el primer caso sería positiva (el campo favorece el movimiento), en el segundo ligeramente negativa (el campo se opone al movimiento) y en el tercero la integral sería nula, al ser el campo ortogonal a la trayectoria. A continuación se comprueban esas intuiciones.

t = sp.symbols('t')
c = vec.ParametricRegion((t,t), (t, 0, 1))
F = S.i + 2 * S.j
print('Trabajo:',vec.vector_integrate(F, c))

Trabajo: 3

F = -2*S.i + S.j
print('Trabajo:',vec.vector_integrate(F, c))

Trabajo: -1

F = -S.i + S.j
print('Trabajo:',vec.vector_integrate(F, c))

Trabajo: 0

Propiedades de las integrales de línea de campos vectoriales

Las integrales curvilíneas sobre campos vectoriales cumplen propiedades análogas a las presentadas para el caso de campos escalares, es decir:

• Si \(\vec{F}_1\) y \(\vec{F}_2\) son dos campos vectoriales y \(C\) una curva regular, entonces

\[\int_C (\lambda \vec{F}_1+\mu \vec{F}_2)\circ d\vec{r}=\lambda \int_C \vec{F}_1\circ d\vec{r} +\mu \int_C \vec{F}_2\circ d\vec{r}\;\;\;\forall \lambda,\mu\in R\]

• Si \(C_1\) y \(C_2\) son dos curvas que no se solapan (salvo en los extremos) y \(\vec{F}\) es un campo vectorial

\[\int_{C_1+C_2} \vec{F}\circ d\vec{r} = \int_{C_1} \vec{F}\circ d\vec{r}+\int_{C_2} \vec{F}\circ d\vec{r}\]

• Si \(C\) es una curva y \(-C\) la curva recorrida en sentido contrario, entonces

\[\int_{-C} \vec{F}\circ d\vec{r} = -\int_{C} \vec{F}\circ d\vec{r}\]

• Si el campo vectorial \(\vec{F}\) está acotado sobre los puntos de la curva \(C\), es decir, existe \(M\in R\) tal que \(\|\vec{F}(\vec{r}(t))\|\leq M\) para todo \(t\in[a,b]\), y \(L_C\) es la longitud de la curva, entonces

\[\left|\int_{C} \vec{F}\circ d\vec{r}\right|\leq M\,L_C\]

Ejercicios propuestos

• Calcular la integral de línea del campo vectorial \(\vec{F}(x,y)=(x^2-2xy)\vec{i}+(y^2-2xy)\vec{j}\) sobre la porción de la parábola \(y=x^2\) que va desde el punto \((-1,1)\) al punto \((1,1)\).

• Calcular la integral de línea a lo largo de la circunferencia \(x^2+y^2=a^2\) recorrida en sentido positivo, del campo vectorial

\[\vec{F}(x,y)=\frac{x+y}{x^2+y^2}\vec{i}+\frac{x+y}{x^2+y^2}\vec{j}\]

• Calcular el trabajo realizado por la fuerza \(\vec{F}(x,y)=(3y^2+2)\vec{i}+16x\vec{j}\) al desplazarse una partícula del punto \((-1,0)\) al punto \((1,0)\) siguiendo la mitad superior de la elipse \(b^2x^2+y^2=b^2\).

• Calcular la integral de línea del campo vectorial \(\vec{F}(x,y)=(2a-y)\vec{i}+x\vec{j}\) sobre el arco de cicloide dado por:

\[\begin{split}\left. \begin{array}{c} x= a(t-\sin t) \\ y= a(1-\cos t) \end{array}\right\}\;\;\; t\in[0,2\pi]\end{split}\]

• Dado el campo vectorial \(\vec{F}(x,y)=(x+y)\vec{i}+(y-x)\vec{j}\) calcular la integral de línea a lo largo de las siguientes curvas que conectan los puntos \((1,1)\) y \((4,2)\):

  • Parábola \(y^2=x\).

  • Segmento de recta que une ambos puntos.

  • Segmentos desde \((1,1)\) a \((1,2)\) y desde \((1,2)\) a \((4,2)\).

  • Curva dada por \(\vec{r}(t)=(2t^2+t+1,t^2+1)\).