Métodos numéricos de resolución de ecuaciones diferenciales de orden 2 o superior#
Al igual que ocurría con las ecuaciones de orden 1, en las de orden superior es habitual encontrarnos con ecuaciones que no admiten una resolución analítica que conduzca a una expresión explícita simbólica de la función solución.
Este problema se puede plantear tanto en ecuaciones lineales como, especialmente, en ecuaciones no lineales, que resultan mucho más complejas de resolver.
En estos casos la alternativa puede ser de nuevo la aproximación numérica de la solución que cumpla determinadas condiciones.
Dentro del módulo de integración (integrate) del paquete SciPy se dispone de la función solve_ivp() que resuelve problemas de valor inicial del tipo
\[\begin{split}\left\{
\begin{array}{l}
\frac{dy}{dt}=f(t,y)\\
y(t_0)=y_0
\end{array}
\right.
\end{split}\]
Esta función se aplica únicamente a problemas de orden 1, pero permite trabajar simultáneamente con varias funciones incógnitas, por lo que una opción puede ser la transformación de una ecuación de orden \(n\) en \(n\) ecuaciones de orden \(1\) y usar la función solve_ivp(). La mejor forma de verlo es a través de algunos sencillos ejemplos.
Ejemplo:
Como primer ejemplo se considera un problema no lineal de segundo orden. En este caso, para determinar una única solución se necesitaría dar dos condiciones iniciales. En concreto se plantea el siguiente problema de valor inicial:
\[\begin{split}\left\{
\begin{array}{l}
y''+ xy'+20 sin(y)=0\\
y(0)=0\\
y'(0)=1
\end{array}
\right.
\end{split}\]
Al ser una ecuación no lineal es dificil resolverlo de manera simbólica. Incluso con el paquete SymPy resulta imposible obtener la solución:
import sympy as sp
try:
x = sp.Symbol('x')
y = sp.Function('y')
edo = sp.Eq(y(x).diff(x,2) + x*y(x).diff(x) + 20*sp.sin(y(x)), 0)
condiciones = {y(0):0, y(x).diff(x).subs(x,0):1}
sp.dsolve(edo, ics=condiciones)
except Exception:
print('No puedo resolver la ecuación')
No puedo resolver la ecuación
La alternativa de resolución en este caso es recurrir a una aproximación numérica de la solución en un intervalo predefinido. Pero para ello es necesario convertir la ecuación de grado 2 en dos ecuaciones de primer grado con dos funciones incógnita \(y_1\), \(y_2\).
Eso se puede conseguir haciendo los siguientes cambios
\[y_1=y\]
\[y_2=y'\]
De esta manera, el problema se podría plantear como
\[\begin{split}\left\{
\begin{array}{l}
\frac{dy_1}{dx} = y_2\\
\frac{dy_2}{dx} = -xy_2-20\sin(y_1)\\
y_1(0)=0;\;y_2(0)=1
\end{array}
\right.
\end{split}\]
Ese problema puede ser resuelto numéricamente con solve_ivp(). Para ello se necesita previamente definir una función \(f(x,Y)\) que devuelva los valores de las dos derivadas de las dos componentes del vector \(Y=(y_1,y_2)\) de acuerdo a las ecuaciones diferenciales:
import numpy as np
def Fproblema(x, Y):
y1, y2 = Y
return [y2, -x*y2-20*np.sin(y1)]
El siguiente paso es definir el intervalo en el que se quiere realizar la aproximación, siendo el extremo inferior de ese intervalo el valor \(x_0\) (en este caso \(0)\), y además un vector con los valores de las dos funciones en ese punto inicial (\(y_1(x_0)\) y \(y_2(x_0)\)):
intervalo = [0, 6]
valoresIniciales = [0, 1]
Una vez que se tienen todos los elementos, lo único que se necesita es importar la función solve_ivp() del módulo de integración de SciPy y hacer la llamada correspondiente. En este caso se va a solicitar al algorimto que aproxime también la solución en una serie de puntos intermedios del intervalo de integración. Estos puntos se incluyen con el parámetro t_eval.
from scipy.integrate import solve_ivp
xs = np.linspace(0, 6, 100)
solucion = solve_ivp(Fproblema, intervalo, valoresIniciales, t_eval=xs)
print(solucion)
message: 'The solver successfully reached the end of the integration interval.'
nfev: 206
njev: 0
nlu: 0
sol: None
status: 0
success: True
t: array([0. , 0.06060606, 0.12121212, 0.18181818, 0.24242424,
0.3030303 , 0.36363636, 0.42424242, 0.48484848, 0.54545455,
0.60606061, 0.66666667, 0.72727273, 0.78787879, 0.84848485,
0.90909091, 0.96969697, 1.03030303, 1.09090909, 1.15151515,
1.21212121, 1.27272727, 1.33333333, 1.39393939, 1.45454545,
1.51515152, 1.57575758, 1.63636364, 1.6969697 , 1.75757576,
1.81818182, 1.87878788, 1.93939394, 2. , 2.06060606,
2.12121212, 2.18181818, 2.24242424, 2.3030303 , 2.36363636,
2.42424242, 2.48484848, 2.54545455, 2.60606061, 2.66666667,
2.72727273, 2.78787879, 2.84848485, 2.90909091, 2.96969697,
3.03030303, 3.09090909, 3.15151515, 3.21212121, 3.27272727,
3.33333333, 3.39393939, 3.45454545, 3.51515152, 3.57575758,
3.63636364, 3.6969697 , 3.75757576, 3.81818182, 3.87878788,
3.93939394, 4. , 4.06060606, 4.12121212, 4.18181818,
4.24242424, 4.3030303 , 4.36363636, 4.42424242, 4.48484848,
4.54545455, 4.60606061, 4.66666667, 4.72727273, 4.78787879,
4.84848485, 4.90909091, 4.96969697, 5.03030303, 5.09090909,
5.15151515, 5.21212121, 5.27272727, 5.33333333, 5.39393939,
5.45454545, 5.51515152, 5.57575758, 5.63636364, 5.6969697 ,
5.75757576, 5.81818182, 5.87878788, 5.93939394, 6. ])
t_events: None
y: array([[ 0.00000000e+00, 5.98315044e-02, 1.15089818e-01,
1.61632088e-01, 1.95940392e-01, 2.15628063e-01,
2.19556874e-01, 2.07656328e-01, 1.81099616e-01,
1.42385383e-01, 9.47827786e-02, 4.21257752e-02,
-1.14868580e-02, -6.19836096e-02, -1.05691452e-01,
-1.39641610e-01, -1.61910838e-01, -1.71531281e-01,
-1.68444153e-01, -1.53669365e-01, -1.29147660e-01,
-9.73123775e-02, -6.10079172e-02, -2.32377082e-02,
1.30889376e-02, 4.54099704e-02, 7.17529021e-02,
9.07115375e-02, 1.01559221e-01, 1.04330401e-01,
9.96226642e-02, 8.85172010e-02, 7.25021738e-02,
5.32741175e-02, 3.26024543e-02, 1.21313318e-02,
-6.72439712e-03, -2.27864439e-02, -3.52187487e-02,
-4.36380724e-02, -4.79845488e-02, -4.84776653e-02,
-4.56110855e-02, -4.00735515e-02, -3.26469560e-02,
-2.41343034e-02, -1.52866746e-02, -6.78778165e-03,
8.05773779e-04, 7.12300644e-03, 1.19295539e-02,
1.51293637e-02, 1.67743044e-02, 1.70193275e-02,
1.60959830e-02, 1.42743417e-02, 1.18400800e-02,
9.07538405e-03, 6.24273949e-03, 3.54470758e-03,
1.13447790e-03, -8.72226418e-04, -2.41645824e-03,
-3.49005777e-03, -4.11490173e-03, -4.34193085e-03,
-4.23867292e-03, -3.88153119e-03, -3.35269961e-03,
-2.72613814e-03, -2.06273123e-03, -1.41640989e-03,
-8.28471262e-04, -3.24024774e-04, 8.29462896e-05,
3.87862148e-04, 5.94488493e-04, 7.12752094e-04,
7.56478542e-04, 7.42034429e-04, 6.84420293e-04,
5.97659067e-04, 4.95587240e-04, 3.89184866e-04,
2.86123059e-04, 1.92339395e-04, 1.11675924e-04,
4.59004435e-05, -4.66086170e-06, -4.09813529e-05,
-6.47982393e-05, -7.79503769e-05, -8.23994276e-05,
-8.04389150e-05, -7.41940645e-05, -6.52639645e-05,
-5.48509014e-05, -4.41491543e-05, -3.39598596e-05,
-2.47742247e-05],
[ 1.00000000e+00, 9.61716948e-01, 8.50178507e-01,
6.75024405e-01, 4.50920398e-01, 1.96246513e-01,
-6.84040958e-02, -3.22062078e-01, -5.45302680e-01,
-7.21635512e-01, -8.38564186e-01, -8.88143743e-01,
-8.68957154e-01, -7.85801416e-01, -6.47895194e-01,
-4.68484395e-01, -2.64113274e-01, -5.20235398e-02,
1.50837027e-01, 3.29658736e-01, 4.72446626e-01,
5.70428854e-01, 6.19108982e-01, 6.18668683e-01,
5.72871607e-01, 4.88838843e-01, 3.76455873e-01,
2.46910778e-01, 1.11705971e-01, -1.84771490e-02,
-1.34215340e-01, -2.27979727e-01, -2.95203481e-01,
-3.33829295e-01, -3.43955517e-01, -3.28036168e-01,
-2.90507030e-01, -2.36808938e-01, -1.73021852e-01,
-1.05156303e-01, -3.87972776e-02, 2.11709919e-02,
7.12121603e-02, 1.09123626e-01, 1.33761394e-01,
1.45221536e-01, 1.44705618e-01, 1.34084648e-01,
1.15728941e-01, 9.21983026e-02, 6.60645330e-02,
3.97346257e-02, 1.51275730e-02, -6.29353740e-03,
-2.34694056e-02, -3.58899323e-02, -4.35699063e-02,
-4.68114963e-02, -4.62134394e-02, -4.25390582e-02,
-3.66425100e-02, -2.94039834e-02, -2.16128979e-02,
-1.39142538e-02, -6.85099234e-03, -8.12766838e-04,
3.99727195e-03, 7.50550852e-03, 9.74122444e-03,
1.08222167e-02, 1.09280480e-02, 1.02710803e-02,
9.07768036e-03, 7.55006214e-03, 5.87044414e-03,
4.19939817e-03, 2.65237030e-03, 1.30242094e-03,
1.97709826e-04, -6.44817111e-04, -1.23184424e-03,
-1.58768389e-03, -1.74731183e-03, -1.75120892e-03,
-1.63785690e-03, -1.44597491e-03, -1.21118979e-03,
-9.60748046e-04, -7.15202307e-04, -4.90640933e-04,
-2.96976534e-04, -1.38694600e-04, -1.60879442e-05,
7.23528632e-05, 1.30944418e-04, 1.64148342e-04,
1.76651663e-04, 1.73995740e-04, 1.61121722e-04,
1.41819054e-04]])
y_events: None
Entre la información que devuelve solve_ivp() está el vector y con los valores de las soluciones \(y_1\) e \(y_2\) correspondientes a los diferentes valores de la variable independiente \(x\). Realmente, en este caso la solución incógnita inicial corresponde solo a la primera componente de ese vector, ya que \(y=y_1\).
solucion.y[0]
array([ 0.00000000e+00, 5.98315044e-02, 1.15089818e-01, 1.61632088e-01,
1.95940392e-01, 2.15628063e-01, 2.19556874e-01, 2.07656328e-01,
1.81099616e-01, 1.42385383e-01, 9.47827786e-02, 4.21257752e-02,
-1.14868580e-02, -6.19836096e-02, -1.05691452e-01, -1.39641610e-01,
-1.61910838e-01, -1.71531281e-01, -1.68444153e-01, -1.53669365e-01,
-1.29147660e-01, -9.73123775e-02, -6.10079172e-02, -2.32377082e-02,
1.30889376e-02, 4.54099704e-02, 7.17529021e-02, 9.07115375e-02,
1.01559221e-01, 1.04330401e-01, 9.96226642e-02, 8.85172010e-02,
7.25021738e-02, 5.32741175e-02, 3.26024543e-02, 1.21313318e-02,
-6.72439712e-03, -2.27864439e-02, -3.52187487e-02, -4.36380724e-02,
-4.79845488e-02, -4.84776653e-02, -4.56110855e-02, -4.00735515e-02,
-3.26469560e-02, -2.41343034e-02, -1.52866746e-02, -6.78778165e-03,
8.05773779e-04, 7.12300644e-03, 1.19295539e-02, 1.51293637e-02,
1.67743044e-02, 1.70193275e-02, 1.60959830e-02, 1.42743417e-02,
1.18400800e-02, 9.07538405e-03, 6.24273949e-03, 3.54470758e-03,
1.13447790e-03, -8.72226418e-04, -2.41645824e-03, -3.49005777e-03,
-4.11490173e-03, -4.34193085e-03, -4.23867292e-03, -3.88153119e-03,
-3.35269961e-03, -2.72613814e-03, -2.06273123e-03, -1.41640989e-03,
-8.28471262e-04, -3.24024774e-04, 8.29462896e-05, 3.87862148e-04,
5.94488493e-04, 7.12752094e-04, 7.56478542e-04, 7.42034429e-04,
6.84420293e-04, 5.97659067e-04, 4.95587240e-04, 3.89184866e-04,
2.86123059e-04, 1.92339395e-04, 1.11675924e-04, 4.59004435e-05,
-4.66086170e-06, -4.09813529e-05, -6.47982393e-05, -7.79503769e-05,
-8.23994276e-05, -8.04389150e-05, -7.41940645e-05, -6.52639645e-05,
-5.48509014e-05, -4.41491543e-05, -3.39598596e-05, -2.47742247e-05])
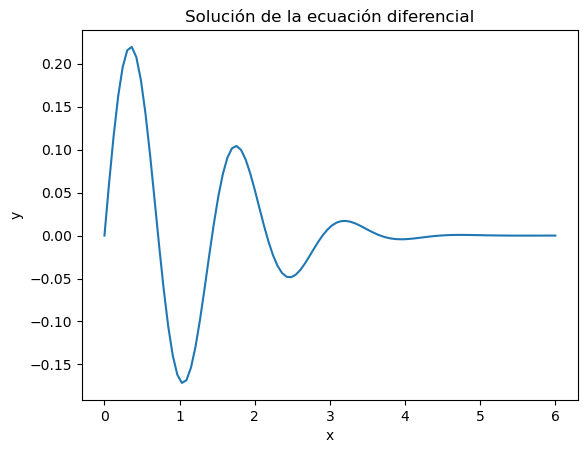
Los valores de \(x\) junto con los de \(y\) pueden representarse gráficamente:
import matplotlib.pyplot as plt
import numpy as np
plt.plot(xs, solucion.y[0])
plt.xlabel('x'); plt.ylabel('y')
plt.title('Solución de la ecuación diferencial')
plt.show()
Ejemplo:
En este segundo ejemplo se considera un problema de valor inicial que sí que puede resolverse simbólicamente. En este caso es una ecuación lineal de segundo orden con coeficientes constantes:
\[\begin{split}\left\{
\begin{array}{l}
y''' + y'' + y' + y = x\\
y(\pi)=1\\
y'(\pi)=1\\
y''(\pi)=0
\end{array}
\right.\end{split}\]
La solución exacta del problema es:
x = sp.Symbol('x')
y = sp.Function('y')
edo = sp.Eq(y(x).diff(x,3) + y(x).diff(x,2) + y(x).diff(x) + y(x), x)
condiciones = {y(sp.pi):1,
y(x).diff(x).subs(x,sp.pi):1,
y(x).diff(x,2).subs(x,sp.pi):0}
sp.dsolve(edo, ics=condiciones)
\[\displaystyle y{\left(x \right)} = x + \left(-1 + \frac{\pi}{2}\right) \sin{\left(x \right)} + \left(-1 + \frac{\pi}{2}\right) \cos{\left(x \right)} - 1 + \left(- \frac{\pi e^{\pi}}{2} + e^{\pi}\right) e^{- x}\]
A partir de la expresión simbólica de la solución se puede definir una función numérica que permita evaluar la solución en cualquier punto.
solexacta = sp.lambdify(x, sp.dsolve(edo, ics=condiciones).rhs)
Con los cambios \(y_1=y\), \(y_2=y'\), \(y_3=y''\) el problema equivalente sería:
\[\begin{split}\left\{
\begin{array}{l}
y_1'=y_2\\
y_2'=y_3\\
y_3'=x-y_1-y_2-y_3\\
y_1(\pi)=1,\;y_2(\pi)=1,\;y_3(\pi)=0
\end{array}
\right.\end{split}\]
La resolución numérica del problema es la siguiente:
def Fproblema(x, Y):
y1, y2, y3 = Y
return [y2, y3, x-y1-y2-y3]
intervalo = [np.pi, 8*np.pi]
valoresIniciales = [1, 1, 0]
xs = np.linspace(np.pi, 8*np.pi, 100)
solucion = solve_ivp(Fproblema, intervalo, valoresIniciales, t_eval=xs)
print(solucion)
message: 'The solver successfully reached the end of the integration interval.'
nfev: 176
njev: 0
nlu: 0
sol: None
status: 0
success: True
t: array([ 3.14159265, 3.36372547, 3.58585828, 3.8079911 , 4.03012391,
4.25225672, 4.47438954, 4.69652235, 4.91865516, 5.14078798,
5.36292079, 5.58505361, 5.80718642, 6.02931923, 6.25145205,
6.47358486, 6.69571768, 6.91785049, 7.1399833 , 7.36211612,
7.58424893, 7.80638175, 8.02851456, 8.25064737, 8.47278019,
8.694913 , 8.91704581, 9.13917863, 9.36131144, 9.58344426,
9.80557707, 10.02770988, 10.2498427 , 10.47197551, 10.69410833,
10.91624114, 11.13837395, 11.36050677, 11.58263958, 11.8047724 ,
12.02690521, 12.24903802, 12.47117084, 12.69330365, 12.91543646,
13.13756928, 13.35970209, 13.58183491, 13.80396772, 14.02610053,
14.24823335, 14.47036616, 14.69249898, 14.91463179, 15.1367646 ,
15.35889742, 15.58103023, 15.80316305, 16.02529586, 16.24742867,
16.46956149, 16.6916943 , 16.91382711, 17.13595993, 17.35809274,
17.58022556, 17.80235837, 18.02449118, 18.246624 , 18.46875681,
18.69088963, 18.91302244, 19.13515525, 19.35728807, 19.57942088,
19.8015537 , 20.02368651, 20.24581932, 20.46795214, 20.69008495,
20.91221776, 21.13435058, 21.35648339, 21.57861621, 21.80074902,
22.02288183, 22.24501465, 22.46714746, 22.68928028, 22.91141309,
23.1335459 , 23.35567872, 23.57781153, 23.79994435, 24.02207716,
24.24420997, 24.46634279, 24.6884756 , 24.91060841, 25.13274123])
t_events: None
y: array([[ 1.00000000e+00, 1.22410323e+00, 1.45909553e+00,
1.71332615e+00, 1.99243314e+00, 2.29934147e+00,
2.63452180e+00, 2.99620619e+00, 3.38042174e+00,
3.78155348e+00, 4.19263555e+00, 4.60603605e+00,
5.01363506e+00, 5.40717260e+00, 5.77916545e+00,
6.12247579e+00, 6.43165245e+00, 6.70302003e+00,
6.93473669e+00, 7.12655321e+00, 7.27973733e+00,
7.39770413e+00, 7.48604318e+00, 7.55178989e+00,
7.60242658e+00, 7.64637421e+00, 7.69243588e+00,
7.74935412e+00, 7.82532605e+00, 7.92762932e+00,
8.06206138e+00, 8.23272861e+00, 8.44237613e+00,
8.69194800e+00, 8.98005855e+00, 9.30304245e+00,
9.65590627e+00, 1.00324839e+01, 1.04254295e+01,
1.08263099e+01, 1.12258844e+01, 1.16157078e+01,
1.19873692e+01, 1.23335785e+01, 1.26483423e+01,
1.29272341e+01, 1.31674106e+01, 1.33676185e+01,
1.35289272e+01, 1.36547223e+01, 1.37498447e+01,
1.38203148e+01, 1.38734263e+01, 1.39175682e+01,
1.39616611e+01, 1.40143795e+01, 1.40841189e+01,
1.41782609e+01, 1.43030326e+01, 1.44631489e+01,
1.46620122e+01, 1.49008059e+01, 1.51784195e+01,
1.54918863e+01, 1.58369825e+01, 1.62079408e+01,
1.65974666e+01, 1.69968623e+01, 1.73975787e+01,
1.77907861e+01, 1.81681522e+01, 1.85221259e+01,
1.88461860e+01, 1.91354424e+01, 1.93862299e+01,
1.95971069e+01, 1.97689238e+01, 1.99044206e+01,
2.00075868e+01, 2.00839864e+01, 2.01407462e+01,
2.01864607e+01, 2.02296792e+01, 2.02792132e+01,
2.03434717e+01, 2.04301494e+01, 2.05459164e+01,
2.06959783e+01, 2.08841580e+01, 2.11120688e+01,
2.13791091e+01, 2.16829827e+01, 2.20200043e+01,
2.23847622e+01, 2.27701004e+01, 2.31675382e+01,
2.35687204e+01, 2.39648103e+01, 2.43473891e+01,
2.47085258e+01],
[ 1.00000000e+00, 1.02607187e+00, 1.09594721e+00,
1.19730694e+00, 1.31789774e+00, 1.44600394e+00,
1.57073920e+00, 1.68233278e+00, 1.77227683e+00,
1.83394226e+00, 1.86218222e+00, 1.85394783e+00,
1.80853446e+00, 1.72751331e+00, 1.61406877e+00,
1.47283172e+00, 1.31000723e+00, 1.13337336e+00,
9.51797503e-01, 7.73622324e-01, 6.07514663e-01,
4.61359805e-01, 3.42173163e-01, 2.55719036e-01,
2.06201185e-01, 1.96141666e-01, 2.25839275e-01,
2.93585158e-01, 3.96179217e-01, 5.28704294e-01,
6.84534139e-01, 8.55852835e-01, 1.03427288e+00,
1.21107028e+00, 1.37765557e+00, 1.52566871e+00,
1.64805962e+00, 1.73847872e+00, 1.79234929e+00,
1.80718431e+00, 1.78257196e+00, 1.71972757e+00,
1.62136697e+00, 1.49213447e+00, 1.33862558e+00,
1.16876763e+00, 9.90655531e-01, 8.13008750e-01,
6.44428263e-01, 4.93355892e-01, 3.67122347e-01,
2.72090624e-01, 2.13017581e-01, 1.92638792e-01,
2.11725295e-01, 2.69512627e-01, 3.63409491e-01,
4.88764775e-01, 6.39058249e-01, 8.07017903e-01,
9.84467296e-01, 1.16282471e+00, 1.33317812e+00,
1.48723481e+00, 1.61729552e+00, 1.71681253e+00,
1.78101771e+00, 1.80695121e+00, 1.79349471e+00,
1.74091830e+00, 1.65157636e+00, 1.53003489e+00,
1.38276126e+00, 1.21676582e+00, 1.04009054e+00,
8.61268790e-01, 6.89263890e-01, 5.32502507e-01,
3.98749386e-01, 2.94747216e-01, 2.25490587e-01,
1.94205014e-01, 2.02285665e-01, 2.49681086e-01,
3.34258213e-01, 4.51668889e-01, 5.95748783e-01,
7.59637244e-01, 9.35393604e-01, 1.11447491e+00,
1.28787274e+00, 1.44723302e+00, 1.58447813e+00,
1.69285291e+00, 1.76717065e+00, 1.80394063e+00,
1.80137260e+00, 1.75918679e+00, 1.67935794e+00,
1.56615154e+00],
[ 0.00000000e+00, 2.25448015e-01, 3.94759361e-01,
5.08404496e-01, 5.68175644e-01, 5.77074739e-01,
5.38910426e-01, 4.59153176e-01, 3.45050056e-01,
2.04660445e-01, 4.65619573e-02, -1.20152237e-01,
-2.86003650e-01, -4.41548436e-01, -5.78652988e-01,
-6.89668169e-01, -7.68646259e-01, -8.11436669e-01,
-8.15787186e-01, -7.81263781e-01, -7.08961847e-01,
-6.02129085e-01, -4.66198060e-01, -3.08083188e-01,
-1.35203052e-01, 4.40870704e-02, 2.21042718e-01,
3.86968707e-01, 5.33699024e-01, 6.53983177e-01,
7.42047901e-01, 7.93806564e-01, 8.06526554e-01,
7.79274413e-01, 7.13445668e-01, 6.12714633e-01,
4.82080459e-01, 3.27712996e-01, 1.56961607e-01,
-2.17369503e-02, -1.99138913e-01, -3.66797597e-01,
-5.16300650e-01, -6.40356914e-01, -7.32971685e-01,
-7.89717476e-01, -8.07750650e-01, -7.85817401e-01,
-7.24986609e-01, -6.28643428e-01, -5.01628709e-01,
-3.49962565e-01, -1.80938466e-01, -2.94531944e-03,
1.75096357e-01, 3.44512198e-01, 4.96906793e-01,
6.24898503e-01, 7.22260285e-01, 7.84277391e-01,
8.07547384e-01, 7.90886931e-01, 7.35406414e-01,
6.44072695e-01, 5.21109453e-01, 3.72284108e-01,
2.04891253e-01, 2.76285223e-02, -1.50954985e-01,
-3.22029537e-01, -4.77262794e-01, -6.09103661e-01,
-7.11030902e-01, -7.78154486e-01, -8.06809117e-01,
-7.95553292e-01, -7.45237325e-01, -6.58601286e-01,
-5.39634684e-01, -3.93901481e-01, -2.28528433e-01,
-5.21101715e-02, 1.26804173e-01, 2.99402976e-01,
4.57277324e-01, 5.92732461e-01, 6.99098268e-01,
7.71169119e-01, 8.05122228e-01, 7.99344300e-01,
7.54436802e-01, 6.72696011e-01, 5.57807203e-01,
4.15182158e-01, 2.51976732e-01, 7.66717356e-02,
-1.02377663e-01, -2.76334673e-01, -4.36780716e-01,
-5.75784559e-01]])
y_events: None
for i in range(len(solucion.t)):
print(f"y({solucion.t[i]}) = {solucion.y[0][i]}")
y(3.141592653589793) = 1.0
y(3.3637254674799806) = 1.2241032328540977
y(3.585858281370168) = 1.4590955306518925
y(3.8079910952603555) = 1.713326145949794
y(4.030123909150543) = 1.9924331428584683
y(4.25225672304073) = 2.299341469548255
y(4.474389536930918) = 2.6345217960898064
y(4.6965223508211045) = 2.9962061939334204
y(4.918655164711292) = 3.380421744287321
y(5.140787978601479) = 3.781553482077331
y(5.362920792491667) = 4.192635550384261
y(5.585053606381854) = 4.606036047270521
y(5.807186420272042) = 5.013635057125018
y(6.029319234162229) = 5.40717260269864
y(6.251452048052416) = 5.779165449201557
y(6.473584861942603) = 6.122475789708801
y(6.695717675832791) = 6.431652445286988
y(6.917850489722978) = 6.703020028027806
y(7.139983303613166) = 6.93473668874987
y(7.362116117503353) = 7.126553214645845
y(7.584248931393541) = 7.279737334060936
y(7.806381745283728) = 7.397704129913234
y(8.028514559173916) = 7.486043176390513
y(8.250647373064103) = 7.551789894382541
y(8.47278018695429) = 7.60242657615371
y(8.694913000844478) = 7.64637421478525
y(8.917045814734665) = 7.692435883206827
y(9.139178628624851) = 7.749354115909389
y(9.361311442515039) = 7.8253260462097005
y(9.583444256405226) = 7.927629322228162
y(9.805577070295413) = 8.062061384258902
y(10.027709884185601) = 8.232728609127696
y(10.249842698075788) = 8.44237613030021
y(10.471975511965976) = 8.691947998666958
y(10.694108325856163) = 8.980058545524562
y(10.91624113974635) = 9.303042450366716
y(11.138373953636538) = 9.655906265479405
y(11.360506767526726) = 10.032483871047265
y(11.582639581416913) = 10.425429537806522
y(11.8047723953071) = 10.82630994302675
y(12.026905209197288) = 11.225884396991546
y(12.249038023087476) = 11.615707834721375
y(12.471170836977663) = 11.98736918202354
y(12.69330365086785) = 12.333578528638974
y(12.915436464758038) = 12.648342338239974
y(13.137569278648225) = 12.927234075207052
y(13.359702092538413) = 13.16741059211412
y(13.5818349064286) = 13.367618545931798
y(13.803967720318788) = 13.528927247956835
y(14.026100534208975) = 13.654722253646629
y(14.248233348099163) = 13.749844682544373
y(14.47036616198935) = 13.820314817111143
y(14.692498975879538) = 13.873426295217413
y(14.914631789769725) = 13.917568173312109
y(15.13676460365991) = 13.961661093738812
y(15.358897417550098) = 14.014379493529013
y(15.581030231440286) = 14.084118851294962
y(15.803163045330473) = 14.17826086520326
y(16.025295859220662) = 14.303032628925546
y(16.247428673110846) = 14.46314892608728
y(16.469561487001037) = 14.66201221621722
y(16.69169430089122) = 14.900805856846391
y(16.913827114781412) = 15.178419488371016
y(17.135959928671596) = 15.491886262848706
y(17.358092742561787) = 15.836982512905784
y(17.58022555645197) = 16.207940825711997
y(17.802358370342162) = 16.597466618467504
y(18.024491184232346) = 16.99686226188103
y(18.246623998122537) = 17.39757866297735
y(18.46875681201272) = 17.79078609280627
y(18.690889625902912) = 18.168152214101084
y(18.913022439793096) = 18.522125936267198
y(19.135155253683287) = 18.84618602323198
y(19.35728806757347) = 19.135442448178075
y(19.57942088146366) = 19.38622991350252
y(19.801553695353846) = 19.597106919649914
y(20.023686509244033) = 19.768923780304203
y(20.24581932313422) = 19.904420565585067
y(20.467952137024408) = 20.00758678577628
y(20.690084950914596) = 20.083986404382017
y(20.912217764804783) = 20.140746175374723
y(21.13435057869497) = 20.186460732302372
y(21.356483392585158) = 20.22967920546605
y(21.578616206475346) = 20.27921321887577
y(21.800749020365533) = 20.343471687520655
y(22.02288183425572) = 20.43014936604904
y(22.245014648145908) = 20.545916374323024
y(22.467147462036095) = 20.695978338005926
y(22.689280275926283) = 20.884158044325588
y(22.91141308981647) = 21.11206878724874
y(23.133545903706658) = 21.3791090990204
y(23.355678717596845) = 21.682982705020358
y(23.577811531487033) = 22.020004327002994
y(23.79994434537722) = 22.384762185823455
y(24.022077159267408) = 22.77010042667093
y(24.244209973157595) = 23.16753823677657
y(24.466342787047783) = 23.568720449449227
y(24.68847560093797) = 23.964810273578188
y(24.910608414828157) = 24.347389130574633
y(25.132741228718345) = 24.708525786919708
solucion.y[0] - solexacta(solucion.t)
array([ 0.00000000e+00, 7.82573090e-07, -1.38189011e-06, -1.06301484e-05,
-6.74613439e-06, -2.75398540e-05, -4.99186487e-05, 1.91552175e-05,
1.01734329e-04, 1.73809459e-04, 1.64307390e-04, 2.07098401e-04,
3.62116822e-04, 5.01052873e-04, 7.76275286e-04, 7.75630528e-04,
5.02174673e-04, 1.70514533e-04, 5.35405151e-05, 1.21701929e-04,
-5.62179058e-05, -6.09399956e-04, -1.17185328e-03, -1.36091079e-03,
-1.45452300e-03, -1.52228115e-03, -1.56816613e-03, -1.54307410e-03,
-1.40463435e-03, -1.09228973e-03, -7.34749718e-04, -5.70738706e-04,
-4.06541622e-04, 6.88252473e-05, 7.85518338e-04, 1.27781946e-03,
1.47806626e-03, 1.62976040e-03, 1.96542501e-03, 2.42603508e-03,
2.52957749e-03, 2.54351771e-03, 2.29493226e-03, 1.85277870e-03,
1.34142610e-03, 9.10595982e-04, 5.26831100e-04, -1.58189411e-04,
-1.11929861e-03, -1.91296249e-03, -2.39340416e-03, -2.75828684e-03,
-3.14897932e-03, -3.46314173e-03, -3.51135213e-03, -3.36584716e-03,
-2.96346417e-03, -2.43101314e-03, -1.85713215e-03, -1.33963741e-03,
-5.49045872e-04, 5.15652872e-04, 1.51048132e-03, 2.14604163e-03,
2.65561277e-03, 3.28920764e-03, 4.03444925e-03, 4.38284313e-03,
4.47894227e-03, 4.26396510e-03, 3.82281487e-03, 3.25430771e-03,
2.54386069e-03, 1.84510671e-03, 8.25566817e-04, -4.98057144e-04,
-1.76352405e-03, -2.64112624e-03, -3.35555958e-03, -4.15382255e-03,
-5.03132586e-03, -5.47681716e-03, -5.58854306e-03, -5.34131645e-03,
-4.81994990e-03, -4.11332167e-03, -3.24235909e-03, -2.27109706e-03,
-9.66068939e-04, 5.53419381e-04, 1.89516170e-03, 2.90372317e-03,
3.86104173e-03, 4.95398019e-03, 5.98163176e-03, 6.43266866e-03,
6.54432228e-03, 6.27287857e-03, 5.76141942e-03, 4.98823157e-03])
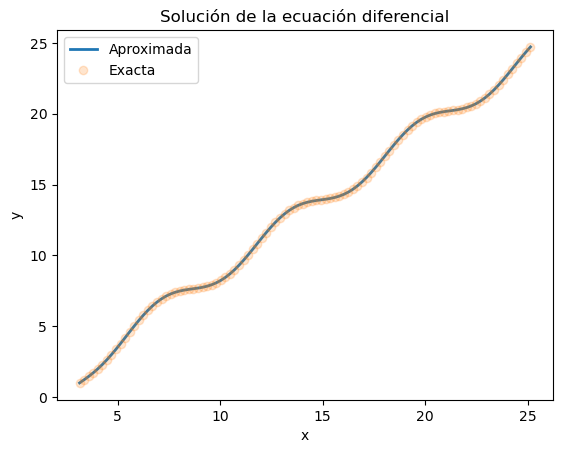
La representación gráfica de la solución obtenida permite una comparación visual con la solución exacta
import matplotlib.pyplot as plt
import numpy as np
plt.plot(solucion.t, solucion.y[0], linewidth=2, label='Aproximada')
plt.plot(solucion.t, solexacta(solucion.t), 'o', label='Exacta', alpha=0.2)
plt.xlabel('x'); plt.ylabel('y')
plt.title('Solución de la ecuación diferencial')
plt.legend()
plt.show()
