Integral de línea de campos escalares

Una vez definidos los conceptos de curva y de campos, escalares y vectoriales, a continuación se pasará a presentar el concepto de integral de campo sobre una curva, también conocido como integral de línea. Para empezar, en esta sección se presentan las integrales de línea sobre campos escalares, dejándose la integración de los campos vectoriales para la próxima sección.

Integral de línea de un campo escalar:

Dado un campo escalar continuo \(F\) y una curva \(C\) regular, contenida en el dominio de \(F\) y parametrizada por \(\vec{r}(t)\) con \(t\in[a,b]\), se define la integral del campo a lo largo de la curva \(C\) como:

\[\int_C F(\vec{r}(t))dr = \int_a^bF(\vec{r}(t))\|\vec{r}\,'(t)\|dt\]

siempre que dicha integral exista.

En el caso de campos escalares y curvas en el plano, la integral de línea sería

\[\int_C F(x,y)dr=\int_a^bF(r_1(t),r_2(t))\|\vec{r}\,'(t)\|dt\]

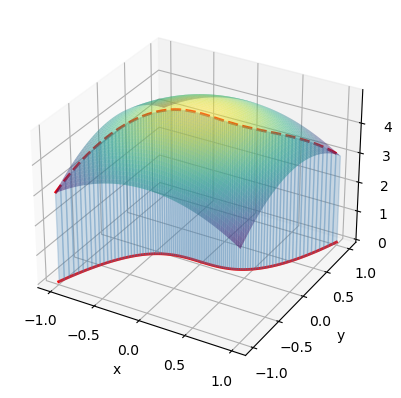
Si además \(F(x,y)\geq 0\) sobre los puntos de la curva, la integral del campo a lo largo de la curva puede interpretarse como el área lateral de la superficie que se genera entre la curva en el plano y la superficie \(z=F(x,y)\).

Por ejemplo, en el caso de considerar \(F(x,y)=5-x^2-y^2\) y la curva \(\vec{r}(t)=(t,t^3)\) con \(t\in[-1,1]\), ese área lateral es el que se visualiza con el siguiente código Python

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d.art3d import Poly3DCollection

F = lambda x,y: 5 - x**2 - y**2
x, y = np.meshgrid(np.linspace(-1, 1, 100), np.linspace(-1, 1, 100))
z = F(x,y)
t = np.linspace(-1, 1, 100)
xc, yc, zc = t, t**3, 0
xs, ys, zs = t, t**3, F(xc,yc)

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_xlabel('x'); ax.set_ylabel('y');

# Gráfico de la superficie
ax.plot_surface(x, y, z, cmap='viridis', alpha=0.5)

# Gráfico de la curva y su imagen sobre la superficie
ax.plot(xc, yc, zc, color='red', linewidth=2)
ax.plot(xs, ys, zs, '--', color='red', linewidth=2)

# Área entre la curva y la superficie
for i in range(len(xc)-1):
    vertices = [(xc[i],yc[i],0), (xc[i+1],yc[i+1],0), (xs[i+1],ys[i+1],zs[i+1]), (xs[i],ys[i],zs[i])]
    ax.add_collection3d(Poly3DCollection([vertices],
                        alpha=0.25, linewidths=1, color='steelblue'))
plt.show()

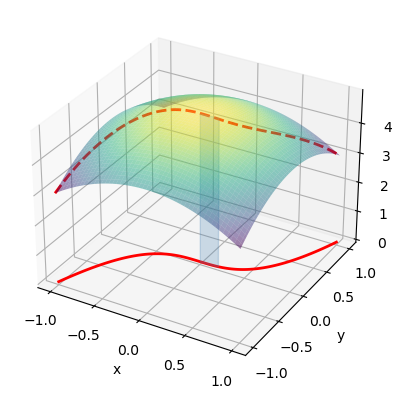
Tal como se ve en la figura que se muestra a continuación, el elemento de área \(\Delta A\) que se forma sobre el tramo de la curva entre los puntos \(\vec{r}(t)\) y \(\vec{r}(t+\Delta t)\) y debajo de la superficie \(z=F(x,y)\) definida por el campo escalar, tiene una superficie de

\[F(r_1(t),r_2(t))\|\vec{r}(t+\Delta t)-\vec{r}(t)\|\]

que puede ser expresado de forma equivalente como

\[F(r_1(t),r_2(t))\left\|\frac{\vec{r}(t+\Delta t)-\vec{r}(t)}{\Delta t}\right\|\Delta t\]

Cuando \(\Delta t\) tiende a cero, la suma de todos los elementos de área de la forma \(\Delta A\) se convierte en la integral

\[\int_a^b F(r_1(t),r_2(t))\left\|\frac{d \vec{r}(t)}{dt}\right\|dt= \int_a^b F(r_1(t),r_2(t))\left\|\vec{r}\,'(t)\right\|dt\]

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_xlabel('x'); ax.set_ylabel('y');
ax.plot_surface(x, y, z, cmap='viridis', alpha=0.5)
ax.plot(xc, yc, zc, color='red', linewidth=2)
ax.plot(xs, ys, zs, '--', color='red', linewidth=2)
t, delta = 0, 0.2
x0, y0 = t, t**3
x1, y1 = t+delta, (t+delta)**3
vertices = [(x0,y0,0), (x1,y1,0), (x1,y1,F(x0,y0)), (x0,y0,F(x0,y0))]
ax.add_collection3d(Poly3DCollection([vertices],
                        alpha=0.25, linewidths=1, color='steelblue'))
plt.show()

---

Ejemplo:

Se calcula a continuación la integral

\[\int_C (5-x^2-y^2)dr\]

siendo \(C\) la curva parametrizada \(\vec{r}(t)=(t,t^3)\) con \(t\in[-1,1]\). De acuerdo a la definición de la integral de línea esa integral sería

\[\int_{-1}^{1}(5-t^2-(t^3)^2)\|(1,3t^2)\|dt = \int_{-1}^{1}(5-t^2-t^6)\sqrt{1+9t^4}dt\]

Esa integral podría calcularse con ayuda de Python

import sympy as sp
t = sp.symbols('t')
sp.integrate((5-t**2-t**6)*sp.sqrt(1+9*t**4), (t,-1,1))

\[\begin{split}\displaystyle \frac{5 \Gamma\left(\frac{1}{4}\right) {{}_{2}F_{1}\left(\begin{matrix} - \frac{1}{2}, \frac{1}{4} \\ \frac{5}{4} \end{matrix}\middle| {9 e^{i \pi}} \right)}}{2 \Gamma\left(\frac{5}{4}\right)} - \frac{\Gamma\left(\frac{3}{4}\right) {{}_{2}F_{1}\left(\begin{matrix} - \frac{1}{2}, \frac{3}{4} \\ \frac{7}{4} \end{matrix}\middle| {9 e^{i \pi}} \right)}}{2 \Gamma\left(\frac{7}{4}\right)} - \frac{\Gamma\left(\frac{7}{4}\right) {{}_{2}F_{1}\left(\begin{matrix} - \frac{1}{2}, \frac{7}{4} \\ \frac{11}{4} \end{matrix}\middle| {9 e^{i \pi}} \right)}}{2 \Gamma\left(\frac{11}{4}\right)}\end{split}\]

sp.integrate((5-t**2-t**6)*sp.sqrt(1+9*t**4), (t,-1,1)).evalf()

\[\displaystyle 13.3440057227365\]

El vector velocidad (\(\vec{r}'(t)\)) y su módulo pueden ser también calculados de una forma más rápida definiendo la velocidad como un campo vectorial y usando la función magnitude. Para ello debe importarse previamente el módulo Vector del paquete Sympy y definir un sistema de coordenadas:

import sympy.vector as vec
S = vec.CoordSys3D('')
t = sp.symbols('t')
x,y = t, t**3
velocidad = sp.diff(x,t)*S.i + sp.diff(y,t)*S.j
F = 5 - x**2 - y**2
sp.integrate(F*velocidad.magnitude(), (t,-1,1)).evalf()

\[\displaystyle 13.3440057227365\]

Otra alternativa para el cálculo de esta integral de linea es usar las funcionalidades de integración vectorial del módulo Vector del paquete Sympy (esta opción puede exigir la actualización del paquete SymPy ejecutando la instrucción !pip install sympy -u). Dentro del módulo se encuentra implementada la función vector_integrate() para realizar integrales de campos escalares o vectoriales sobre regiones que pueden definirse mediante ecuaciones paramétricas o implícitas. La propia función identifica, en función del tipo de región definida, si se debe aplicar una integración de línea o de superficie.

El campo debe definirse también en formato vectorial y la parametrización de la curva puede hacerse directamente con la función ParametricRegion()

c = vec.ParametricRegion((t,t**3), (t, -1, 1))
F = 5 - S.x**2 - S.y**2
integral = vec.vector_integrate(F, c)
print(integral)
integral.evalf()

5*gamma(1/4)*hyper((-1/2, 1/4), (5/4,), 9*exp_polar(I*pi))/(2*gamma(5/4)) - gamma(3/4)*hyper((-1/2, 3/4), (7/4,), 9*exp_polar(I*pi))/(2*gamma(7/4)) - gamma(7/4)*hyper((-1/2, 7/4), (11/4,), 9*exp_polar(I*pi))/(2*gamma(11/4))

\[\displaystyle 13.3440057227365\]

---

Es importante señalar que no toda integral va a poder calcularse de manera simbólica. En tales casos se debería recurrir a los métodos de integración numérica del paquete SciPy para obtener aproximaciones de la integral.

Por supuesto, dependiendo del campo y de la parametrización de la curva, las integrales resultantes pueden llegar a ser extremadamente complejas para ser realizadas “a mano”. No obstante, en casos sencillos sí que se podría realizar.

---

Ejemplo:

Considérese el campo escalar \(F(x,y)=\frac{x^3}{y}\) y la curva \(C\) definida por la parábola \(y=\frac{x^2}{2}\) entre los puntos \((0,0)\) y \((2,2)\). Para calcula la integral del campo sobre la curva, se necesita en primer lugar una parametrización de \(C\):

\[\begin{split}\begin{array}{rl} C:[0,2] &\longrightarrow R^2\\ t &\longrightarrow \vec{r}(t)=(t,t^2/2) \end{array}\end{split}\]

De esta forma, la integral sería:

\[\int_C F(x,y)dr=\int_0^2 F(t,t^2/2)\sqrt{1+t^2}dt=\int_0^2 2t\sqrt{1+t^2}dt\]

que con el cambio de variable \(u=1+t^2\) se transformaría en la integral:

\[=\int_1^5 u^{1/2}du=\left. \frac{u^{(3/2)}}{3/2}\right|^5_1 =\frac{2}{3}(5\sqrt{5}-1)\]

El cálculo de esa integral de linea con el módulo Vector de SymPy se haría de la siguiente manera:

S = vec.CoordSys3D('')
t = sp.symbols('t')
c = vec.ParametricRegion((t, t**2/2), (t, 0, 2))
F = S.x**3 / S.y
integral = vec.vector_integrate(F, c)
print(integral)
integral.evalf()

-2/3 + 10*sqrt(5)/3

\[\displaystyle 6.78689325833263\]

---

Ejemplo:

Calcular la integral de linea del campo escalar \(F(x,y)=10+xy^2\) a lo largo de la circunferencia de centro (0,0) y radio 1.

La primera operación necesaria es la obtención de una parametrización de la curva y el cálculo del módulo de su vector velocidad. En este caso:

\[\vec{r}(t)=(\cos t, \sin t) \mbox{ con }t\in[0,2\pi]\]

\[\vec{r}'(t)=(-\sin t, \cos t)\Rightarrow \|\vec{r}'(t)\|=\sqrt{\sin^2 t + \cos^2 t} = 1\]

Por tanto, la integral a calcular sería:

\[\int_C F(x,y)dr=\int_0^{2\pi} (10+\cos t\sin^2t)dt=\left. 10t+\sin^3t \right|^{2\pi}_0 = 20\pi\]

Con Python puede comprobarse fácilmente con la integración simbólica:

x, y = sp.cos(t), sp.sin(t)
F = 10+x*y**2
velocidad = sp.diff(x,t)*S.i + sp.diff(y,t)*S.j
sp.integrate(F*velocidad.magnitude(), (t,0,2*sp.pi))

\[\displaystyle 20 \pi\]

Otra alternativa es el uso del módulo Vector, que también permite definir curvas a partir de ecuaciones implícitas del tipo \(g(x,y)=0\). En este caso no es necesario definir las ecuaciones paramétricas sino que el propio módulo trata de deducirlas.

x,y = sp.symbols('x,y')
circunferencia = vec.ImplicitRegion((x, y), x**2+y**2-1)
F = 10 + S.x*S.y**2
vec.vector_integrate(F, circunferencia)

\[\displaystyle 20 \pi\]

---

Ejemplo:

Dado el campo escalar \(F(x,y)=2xy^2\) calcular su integral a lo largo del cuadrante de la elipse \((x^2/9)+(y^2/4)=1\), que va desde el punto (3,0) al punto (0,2).

Se pueden realizar dos parametrizaciones equivalentes:

• \(\vec{r}(t)=(t,2\sqrt{1-t^2/9})\) con \(t\in[0,3]\)

• \(\vec{r}(t)=(3\cos t,2\sin t)\) con \(t\in[0,\pi/2]\)

y la integral se podría hacer de varias maneras equivalentes

x, y = t, 2*sp.sqrt(1-t**2/9)
F = 2*x*y**2
velocidad = sp.diff(x,t)*S.i + sp.diff(y,t)*S.j
sp.integrate(F*velocidad.magnitude(), (t,0,3)).evalf()

\[\displaystyle 21.0680741667456\]

Se puede obtener una aproximación de la integral recurriendo a los métodos numéricos de integración implementados en el paquete SciPy. Para ello previamente hay que definir una función numérica con el integrando de la integral.

integrando = F*velocidad.magnitude()
print(integrando)

2*t*(4 - 4*t**2/9)*sqrt(4*t**2/(81*(1 - t**2/9)) + 1)

from scipy import integrate
f = lambda t: 2*t*(4 - 4*t**2/9)*np.sqrt(4*t**2/(81*(1 - t**2/9)) + 1)
integrate.quad(f, 0, 3)

(21.06807416674556, 4.0945025148175773e-10)

Se puede comprobar que con la otra parametrización equivalente de la curva se obtendría el mismo resultado

x, y = 3*sp.cos(t), 2*sp.sin(t)
F = 2*x*y**2
velocidad = sp.diff(x,t)*S.i + sp.diff(y,t)*S.j
sp.simplify(F*velocidad.magnitude())

\[\displaystyle 24 \sqrt{5 \sin^{2}{\left(t \right)} + 4} \sin^{2}{\left(t \right)} \cos{\left(t \right)}\]

f = lambda t: 24*np.sqrt(5*np.sin(t)**2+4)*np.sin(t)**2*np.cos(t)
integrate.quad(f, 0, np.pi/2)

(21.06807416674556, 2.5638562039780468e-11)

---

Aunque todos los casos anteriores corresponden a curvas en el plano y campos bidimensionales, por supuesto la integral de linea también podría realizarse en el caso de campos y curvas en el espacio. En este caso la definición de línea sería

\[\int_C F(x,y,z)dr=\int_a^bF(r_1(t),r_2(t),r_3(t))\|\vec{r}\,'(t)\|dt\]

Tanto el en caso del plano como el espacio la integral curvilínea sobre campos escalares cumple una serie de propiedades básicas:

• La integral curvilínea de un campo escalar solo depende del valor del campo sobre los puntos de la curva y es independiente de la parametrización escogida y del sentido de recorrido de dicha curva.

• Si \(F_1\) y \(F_2\) son dos campos escalares continuos y \(C\) una curva regular, entonces

\[\int_C (\lambda F_1+\mu F_2)dr=\lambda \int_C F_1dr +\mu \int_C F_2dr\;\;\;\forall \lambda,\mu\in R\]

• Si \(C_1\) y \(C_2\) son dos curvas que no se solapan (salvo en los extremos), entendiendo por \(C_1+C_2\) la curva resultante de unir ambas curvas, y \(F\) es un campo escalar continuo

\[\int_{C_1+ C_2} Fdr = \int_{C_1} Fdr+\int_{C_2} Fdr\]

• Si el campo escalar \(F\) está acotado sobre los puntos de la curva \(C\), es decir, existe \(M\in R\) tal que \(|F(\vec{r}(t))|\leq M\) para todo \(t\in[a,b]\), y \(L_C\) es la longitud de la curva, entonces

\[\left|\int_{C} Fdr\right|\leq M\,L_C\]

De hecho, teniendo en cuenta la interpretación del concepto de integral de línea de un campo escalar sobre una curva, la longitud de la curva puede calcularse precisamente considerando el campo escalar uniforme \(F=1\). Es decir,

\[L_C = \int_C dr=\int_a^b\|\vec{r}\,'(t)\|dt\]

En el caso de curvas planas parametrizadas por \(\vec{r}(t)=(r_1(t),r_2(t))\) con \(t\in[a,b]\), la longitud sería

\[L_C = \int_a^b\sqrt{r_1'(t)^2+r_2'(t)^2}dt\]

mientras que para curvas en el espacio la longitud sería

\[L_C = \int_a^b\sqrt{r_1'(t)^2+r_2'(t)^2+r_3'(t)^2}dt\]

Aplicaciones de las integrales curvilíneas de campos escalares

Ya se han comentado algunas de las aplicaciones de las integrales de linea de campos escalares:

• Cálculo de longitudes de curvas

• Cálculo de áreas entre curvas y superficies

Otra de las aplicaciones es el cálculo de masas a partir de densidades lineales. Si la curva \(C\) representa un alambre con densidad lineal \(\rho\), la densidad puede verse como un campo escalar, entonces la masa del alambre es

\[masa(C)=\int_{C} \rho dr\]

Por otro lado, dado un campo escalar \(F\) el valor promedio del campo sobre la curva \(C\) se define como

\[\frac{\int_{C} F\,dr}{L_C}\]

siendo \(L_C\) la longitud de la curva.

En particular, las coordenadas del centro de gravedad de un alambre de densidad lineal \(\rho\) vienen definidas por las expresiones:

\[ x_0=\frac{\int_{C} x\rho dr}{masa(C)};\;\;\;\; y_0=\frac{\int_{C} y\rho dr}{masa(C)};\;\;\;\; z_0=\frac{\int_{C} z\rho dr}{masa(C)} \]

En el caso de un alambre en el plano, se utilizarían las expresiones anteriores pero sin considerar la tercera coordenada \(z_0\).

---

Ejemplo:

Un alambre tiene forma de semicircunferencia de radio \(a\) y la densidad lineal en cada punto del alambre es directamente proporcional a la distancia a la recta que pasa por los extremos del alambre.

Para calcular la masa del alambre se debe establecer una parametrización de la curva. Asumiendo que el origen de coordenadas se sitúa en el centro de la circunferencia, la curva se parametrizaría de la siguiente manera:

\[\begin{split}\begin{array}{rl} C:[0,\pi] &\longrightarrow R^2\\ t &\longrightarrow \vec{r}(t)=(a\cos t,a\sin t) \end{array}\end{split}\]

Además, la distancia a la recta que pasa por los extremos es el valor de la coordenada \(y\), por tanto, la densidad lineal será de la forma

\[\rho(x,y)=ky\]

La masa del alambre se podría calcular de la siguiente manera:

\[masa(C)=\int_{C} \rho dr =\int_0^\pi ka\sin t\sqrt{a^2\sin^2t+a^2\cos^2t}\,dt=ka^2\int_0^\pi \sin t\,dt = 2ka^2\]

---

Ejemplo:

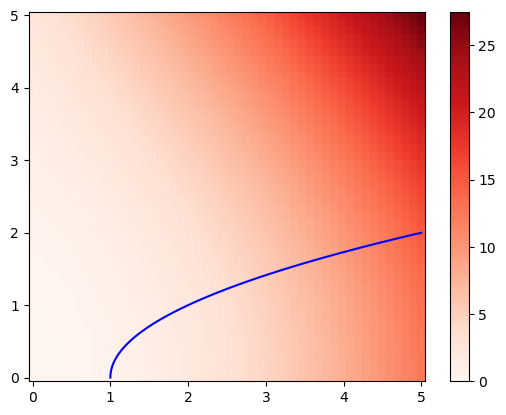
En el plano la temperatura viene dada por la función

\[T(x,y)=\frac{5x^2+y^2(x+1)}{10}\]

y una partícula se mueve entre el origen y el punto \((5,2)\) a través de la curva parabólica \(x=y^2+1\). Para calcular la temperatura media a lo largo de la trayectoria habría que calcular

\[T_{media}=\frac{\int_{C} T(x,y)\,dr}{L_C}\]

siendo \(L_C\) la longitud de la curva.

En primer lugar se necesitaría una parametrización de la curva. Teniendo en cuenta que la variable \(x\) está dada como función de \(y\), la parametrización podría ser:

\[\vec{r}(t)=(t^2+1,t)\mbox{ con }t\in[0,2]\]

Fácilmente puede generarse un mapa de calor y una representación de la curva para observar cómo varía la temperatura a lo largo de la trayectoria.

import matplotlib.pyplot as plt
x, y = np.meshgrid(np.linspace(0, 5), np.linspace(0, 5))
z = (5*x**2+y**2*(x+1))/10
temp = plt.pcolormesh(x, y, z, cmap = 'Reds') 
plt.colorbar(temp)
t = np.linspace(0,2)
plt.plot(t**2+1,t,color='blue')
plt.show()

Para calcular la temperatura media a lo largo de la trayectoria se necesita calcular la longitud de la curva y la integral de linea.

from sympy.geometry import Curve
t = sp.symbols('t')
C = Curve((t**2+1,t), (t, 0, 2))
longitud = C.length
longitud

\[\displaystyle \frac{\operatorname{asinh}{\left(4 \right)}}{4} + \sqrt{17}\]

T = (5*S.x**2+S.y**2*(S.x+1))/10
T

\[\displaystyle \frac{\mathbf{{x}_{}}^{2}}{2} + \frac{\mathbf{{y}_{}}^{2} \left(\mathbf{{x}_{}} + 1\right)}{10}\]

integral = vec.vector_integrate(T, C)
integral

\[\displaystyle \frac{55 \operatorname{asinh}{\left(4 \right)}}{512} + \frac{3981 \sqrt{17}}{640}\]

Tmedia = integral/longitud
Tmedia.evalf()

\[\displaystyle 5.56772699870948\]

Ejercicios propuestos

• Calcular la integral de línea del campo escalar \(F(x,y)=xy^2\) a lo largo de la circunferencia de centro \((0,0)\) y radio 1.

• Calcular la integral \(\int_C \frac{1}{x^2+y^2+4}\,dr\) sobre el segmento \(C\) que une los puntos \((0,0)\) y \((1,2)\).

• Calcular la siguiente integral de línea \(\int_C xy\,dr\) siendo \(C\) el contorno del cuadrado que viene determinado por la condición \(|x|+|y|=1\).

• Dado el campo escalar \(F(x,y)=2xy\), calcular su integral a lo largo del cuadrante de la elipse \(\frac{x^2}{9}+\frac{y^2}{4}=1\) que va desde el punto \((3,0)\) al punto \((0,2)\).

• Calcular la carga total de un alambre cuya forma sigue la curva \(y=x^2\) desde el punto \((0,0)\) hasta el punto \((2,4)\), si la densidad de carga en cada punto viene dada por \(\delta(x,y)=x\).