Curvas parametrizadas

El concepto de curva es algo bastante intuitivo, se puede ver una curva como un subconjunto de puntos del plano o del espacio que tiene una longitud pero no un área o superficie. Pero para poder tratar adecuadamente las curvas se debe definir con más rigor dicho concepto y establecer algunas propiedades deseables. Se comienza por definir el concepto de curva parametrizada en el plano, para posteriormente generalizarlo al caso de curvas en el espacio.

Curva plana parametrizada:

Una curva parametrizada en el plano es una aplicación continua definida en la forma

\[\begin{split}\begin{array}{rl} C:[a,b] &\longrightarrow R^2\\ t &\longrightarrow \vec{r}(t)=(r_1(t),r_2(t)) \end{array} \end{split}\]

A \(t\) se le denomina parámetro, y en ocasiones puede verse como una medida del tiempo. La imagen de la aplicación anterior es un subconjunto de \(R^2\) cuya representación gráfica puede verse como el rastro que deja un móvil que se desplaza por el plano a lo largo del tiempo \(t\), por lo que se denomina trayectoria. A medida que aumenta el valor de \(t\), la posición \(\vec{r}(t)\) se va desplazando según un cierto sentido sobre la curva \(C\). Este sentido de recorrido se llama orientación de la curva \(C\)

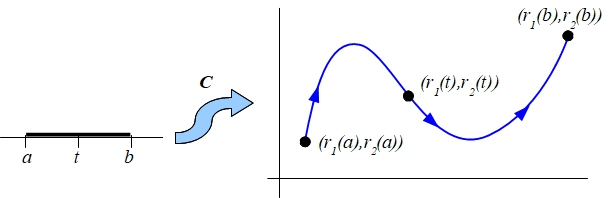
Se llama ecuaciones paramétricas de la curva a las ecuaciones

\[\begin{split}\begin{array}{l} x=r_1(t)\\ y=r_2(t) \end{array}\end{split}\]

Con ayuda del paquete Matplotlib de Python resulta muy sencilla la visualización de estas curvas parametrizadas.

---

Ejemplo:

A continuación se muestran algunos ejemplos de curvas en el plano.

import numpy as np
import matplotlib.pyplot as plt
t = np.linspace(0,1,100)
x, y = t**3/10, 2*t-t**2
plt.plot(x,y)
plt.show()

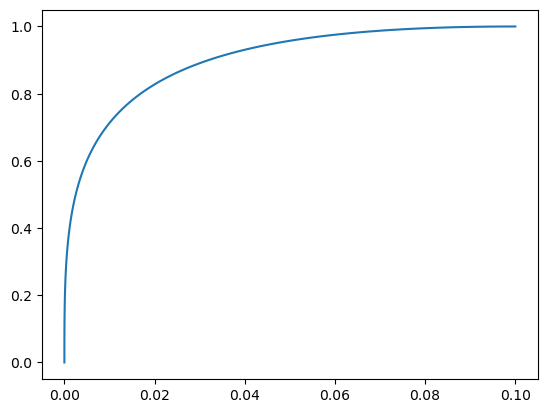
t = np.linspace(0,10,100)
x, y = t**(1/2)*np.sin(t), t*np.cos(t)
plt.plot(x,y)
plt.show()

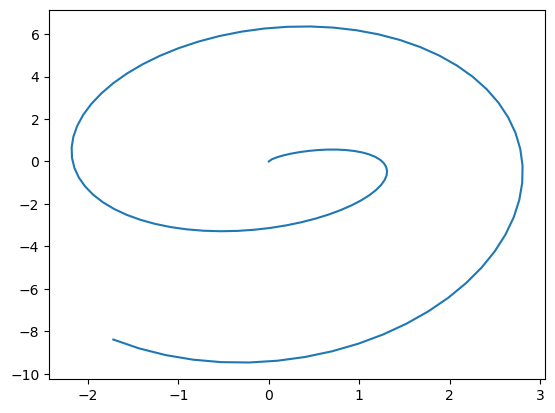
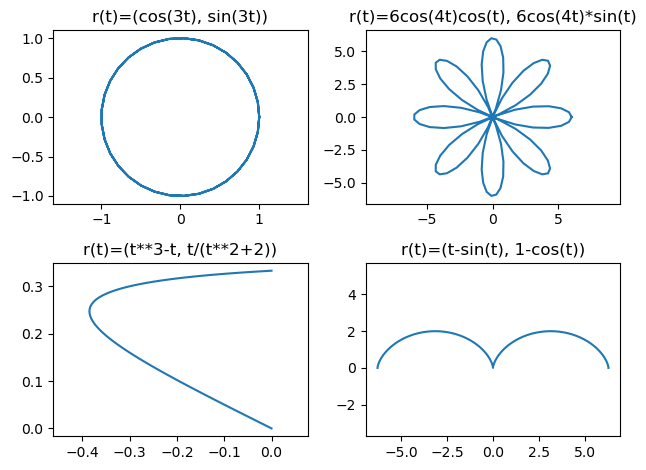
Las curvas siguientes también pueden representarse fácilmente:

\[\begin{split}\begin{array}{ll} \begin{array}{rl} C1:&[0,2\pi] \longrightarrow R^2\\ &t \longrightarrow \vec{r}(t)=(\cos^3t,\sin^3t) \end{array} & \begin{array}{rl} C2:&[0,2\pi] \longrightarrow R^2\\ &t\longrightarrow \vec{r}(t)=(6\cos 4t\,\cos t, 6\cos 4t\,\sin t) \end{array} \\ \begin{array}{rl} C3:&[0,1] \longrightarrow R^2\\ &t\longrightarrow \vec{r}(t)=(t^3-t, t/(t^2+2)) \end{array} & \begin{array}{rl} C4:&[-2\pi,2\pi] \longrightarrow R^2\\ &t\longrightarrow \vec{r}(t)=(t-\sin t, 1-\cos t) \end{array} \end{array} \end{split}\]

fig, ax = plt.subplots(nrows=2, ncols=2)
t = np.linspace(0, 2*np.pi,100)
ax[0,0].axis('equal')
ax[0,0].plot(np.cos(3*t), np.sin(3*t))
ax[0,1].axis('equal')
ax[0,1].plot(6*np.cos(4*t)*np.cos(t), 6*np.cos(4*t)*np.sin(t))
t = np.linspace(0, 1,100)
ax[1,0].axis('equal')
ax[1,0].plot(t**3-t, t/(t**2+2))
t = np.linspace(-2*np.pi, 2*np.pi,100)
ax[1,1].axis('equal')
ax[1,1].plot(t-np.sin(t), 1-np.cos(t))
ax[0,0].set_title("r(t)=(cos(3t), sin(3t))")
ax[0,1].set_title("r(t)=6cos(4t)cos(t), 6cos(4t)*sin(t)")
ax[1,0].set_title("r(t)=(t**3-t, t/(t**2+2))")
ax[1,1].set_title("r(t)=(t-sin(t), 1-cos(t))")
fig.tight_layout()
plt.show()

---

El concepto de curva en el plano es fácilmente generalizable al espacio.

Curva parametrizada en el espacio:

Una curva puede verse con la trayectoria que sigue un móvil que se desplaza por el espacio, de manera que toda curva en el espacio vendrá definida a partir de una parametrización de la forma

\[\begin{split}\begin{array}{rl} \vec{r}:[a,b] &\longrightarrow R^3\\ t &\longrightarrow \vec{r}(t)=(r_1(t),r_2(t),r_3(t)) \end{array} \end{split}\]

Las ecuaciones paramétricas de la curva serán, por tanto

\[\begin{split}\begin{array}{l} x=r_1(t)\\ y=r_2(t)\\ z=r_3(t) \end{array} \end{split}\]

En Python también resulta sencillo obtener representaciones tridimensionales de curvas en el espacio.

---

Ejemplo:

La trayectoria asociada a la curva dada por las siguientes ecuaciones paramétricas:

\[\begin{split} \begin{array}{l} x=7\cos(t)\\ y=9\sin(t)\\ z=t \end{array}\;\;\;\;\mbox{ con }t\in[0,20] \end{split}\]

se podría representar con el siguiente código:

t = np.linspace(0,20,100)
x, y, z = 7*np.cos(t), 9*np.sin(t), t
ax = plt.axes(projection='3d')
ax.plot(x,y,z)
plt.show()

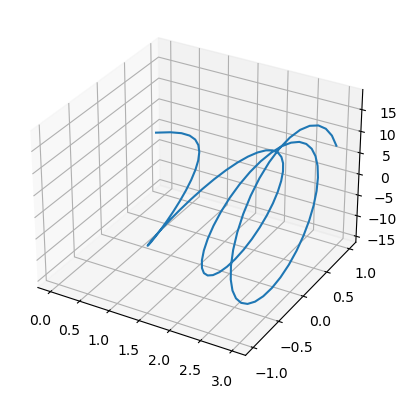
Otro ejemplo podría ser la trayectoria parametrizada por \(\vec{r}(t)=(\log t, \sin t, t\cos t)\) con \(t\in[1,20]\):

t = np.linspace(1,20,100)
x, y, z = np.log(t), np.sin(t), t*np.cos(t)
ax = plt.axes(projection='3d')
ax.plot(x,y,z)
plt.show()

Otra alternativa para representar curvas con Python es utilizar el paquete de computación sibólica SymPy, que tiene un módulo específico para definir curvas paramétricas y realizar con ellas diferentes operaciones. En concreto se trata del módulo sympy.geometry, que puede complementarse con funciones específicas de representación gráfica del módulo sympy.plotting. La utilización de todas estas funcionalidades requiere la importación previa:

import sympy as sp
from sympy.geometry import Curve
from sympy.plotting import plot_parametric, plot3d_parametric_line

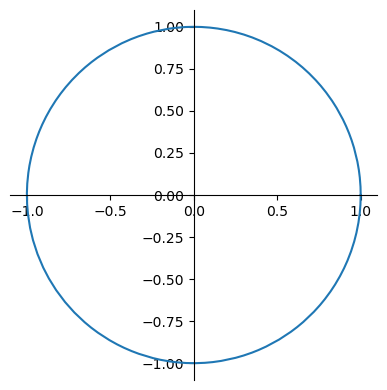
Una vez importados los módulos, la primera operación sería la definición de la curva a partir de sus ecuaciones paramétricas, por ejemplo, a continuación se genera la circunferencia unidad:

t = sp.symbols('t')
C = Curve((sp.cos(t), sp.sin(t)), (t, 0, 2*sp.pi))

Construido el objeto que define la curva, a través de diferentes propiedades se puede acceder a sus ecuaciones paramétricas, el nombre del parámetro, su intervalo de variación o a calcular la longitud de la curva

C.functions

\[\displaystyle \left( \cos{\left(t \right)}, \ \sin{\left(t \right)}\right)\]

C.parameter

\[\displaystyle t\]

C.limits

\[\displaystyle \left( t, \ 0, \ 2 \pi\right)\]

C.length

\[\displaystyle 2 \pi\]

La representación gráfica de la curva con plot_parametric() unicamente requiere señalar las funciones de parametrización y el intervalo de variación del parámetro. Opcionalmente se puede señalar un tamaño para la imagen.

plot_parametric(C.functions, C.limits, size=(4,4));

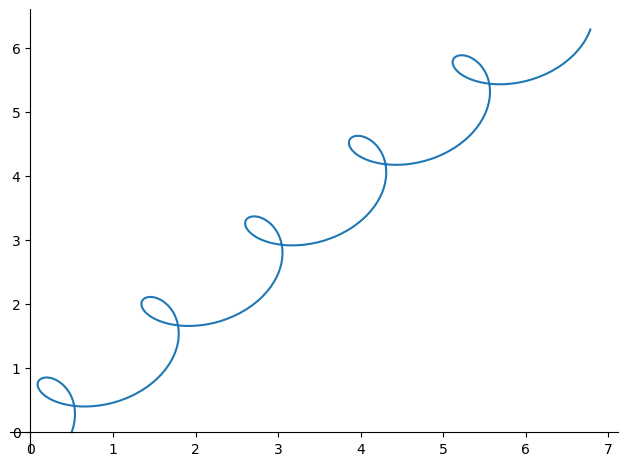
También es posible representar la función sin definir previamente la curva, simplemente señalando las ecuaciones paramétricas. Se puede hacer tanto para curvas en el plano (con la función plot_parametric()) como para curvas en el espacio (con la función plot3d_parametric_line())

x = t + 0.5 * sp.cos(5*t)
y = t + 0.5 * sp.sin(5*t)
plot_parametric(x, y, (t, 0, 2*sp.pi));

x = sp.cos(t)
y = sp.sin(t)
z = t
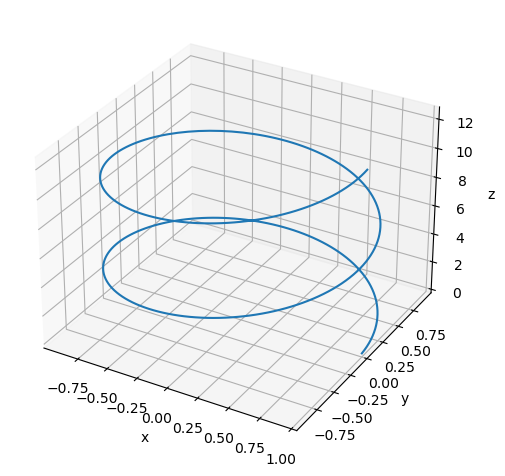
plot3d_parametric_line(x, y, z, (t, 0, 4*sp.pi));

Representación implícita de curvas

Además de la representación paramétrica de una curva, las curvas pueden también expresarse en forma implícita.

En el caso de curvas planas la representación implícita viene dada por expresiones de la forma

\[g(x,y)=0\]

siendo \(g(x,y)\) una función de dos variables. Las curvas planas también pueden aceptar representaciones explícitas de la forma

\[y=f(x)\]

siendo en este caso \(f(x)\) una función de una variable. Evidentemente, es fácil obtener una representación implícita a partir de una explícita, ya que

\[y=f(x)\Leftrightarrow y-f(x)=0\]

Sin embargo, no siempre es posible deducir una representación explícita a partir de una implícita.

El paquete SymPy dispone de la función plot_implicit para representar curvas planas dadas mediante ecuaciones implícitas.

---

Ejemplo:

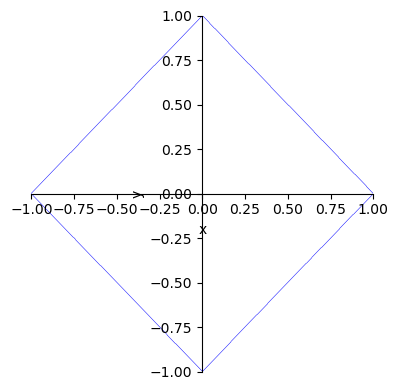
A continuación se muestra la representación de la curva definida por la ecuación

\[|x|+|y|=1\]

Para obtener su representación con SymPy debe definirse previamente un objeto de tipo ecuación:

x,y = sp.symbols('x y')
ecuacion = sp.Eq(abs(x)+abs(y), 1)
sp.plot_implicit(ecuacion, (x,-1,1), (y,-1,1), size=(4,4));

---

En el caso de curvas en el espacio, también pueden venir expresadas mediante ecuaciones implícitas. A diferencia de lo que ocurre con las curvas en el plano, una curva en el espacio necesita para su caracterización dos ecuaciones implícitas:

\[\begin{split} \begin{array}{l} g(x,y,z)=0\\ h(x,y,z)=0 \end{array} \end{split}\]

En este caso puede verse la curva como la intersección de dos superficies. La representación explícita de una curva en el espacio con una única función tampoco es posible, ya que si se consideran representaciones de la forma \(z=f(x,y)\) lo que se obtiene realmente es toda una superficie.

A continuación se incluye un ejemplo en el que se deduce la parametrización de una curva en el espacio dada por dos ecuaciones implícitas.

---

Ejemplo:

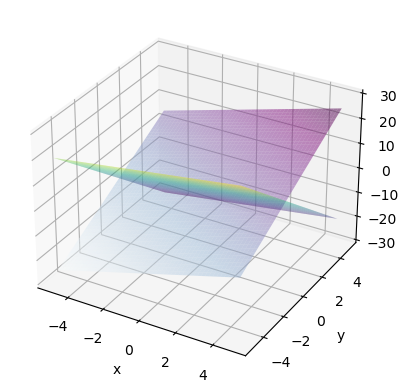
Una recta en el espacio es la intersección de dos planos. Por ejemplo, si se considera la recta resultante de realizar la intersección de los planos:

\[\begin{split} \begin{array}{l} 2x+3y-z=0\\ -x+5y+z=0 \end{array} \end{split}\]

Para obtener unas ecuaciones paramétricas de esta recta, se podría tratar de despejar dos de las variables en función de la tercera en el sistema que definen las dos coordenadas implícitas.

Así de la primera ecuación podría obtenerse \(z=2x+3y\), que llevado a la segunda conduce a

\[-x+5y+2x+3y=0\Rightarrow x=-8y\]

y entonces \(z=2x+3y=-13y\). En definitiva, una parametrización de la recta resultante sería:

\[\vec{r}(t)=(-8t,t,-13t)\]

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_xlabel('x'); ax.set_ylabel('y');
x, y = np.meshgrid(np.linspace(-5, 5), np.linspace(-5, 5))
ax.plot_surface(x, y, 2*x+3*y, alpha=0.5, cmap='BuPu')
ax.plot_surface(x, y, x-5*y, alpha=0.5, cmap='viridis')
plt.show()

Parametrización de algunas curvas básicas

De todas las posibles formas de representar una curva, la expresión paramétrica es la que aporta más información, por lo que suele ser interesante obtener representaciones paramétricas de las curvas. Las ecuaciones paramétricas aportan más información que las ecuaciones cartesianas, ya que estas últimas solo informan sobre los puntos por los que ha pasado el móvil que sigue esa trayectoria, mientras que las ecuaciones paramétricas informan también del punto en el que se encuentra en cada instante de tiempo. Además las ecuaciones paramétricas permiten deducir una orientación o sentido de recorrido de la curva.

Resulta por tanto interesante tratar de representar las curvas en forma paramétrica, sin embargo esa tarea no es en general sencilla. En el caso de curvas planas expresadas de forma explícita \(y=f(x)\) bastaría considerar una parametrización de la forma:

\[\begin{split}\begin{array}{l} x=t\\ y=f(t) \end{array}\end{split}\]

Sin embargo, para la parametrización de una curva expresada de forma implícita no existe un método general, dependerá del tipo de curva. A continuación se ven algunos casos sencillos de parametrizaciones de curvas en el plano:

• Parametrización del segmento entre los extremos \((a_1,a_2)\) y \((b_1,b_2)\):

\[(x,y)=t(a_1,a_2)+(1-t)(b_1,b_2)\;\mbox{ con }t\in[0,1]\]

• Parametrización de la circunferencia de centro \((x_0,y_0)\) y radio \(r\), cuya ecuación implícita es \((x-x_0)^2+(y-y_0)^2=r^2\):

\[(x,y)=(x_0+r\cos t, y_0+r\sin t) \mbox{ con }t\in[0,2\pi]\]

• Parametrización de la elipse de centro \((x_0,y_0)\) y semiejes \(a\) y \(b\), cuya ecuación implícita es \(\frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}=1\):

\[(x,y)=(x_0+a\cos t, y_0+b\sin t) \mbox{ con }t\in[0,2\pi]\]

Propiedades de las curvas parametrizadas

En primer lugar debe advertirse que una misma curva en el plano o en el espacio puede venir parametrizada por diferentes parametrizaciones equivalentes. Dos parametrizaciones se consideran equivalentes cuando se puede transformar una en otra mediante una aplicación biyectiva de clase \(C^1\).

Hay determinados conceptos o propiedades que son intrínsecas a las curvas, y por tanto no dependen de la parametrización elegida, sin embargo otros sí que dependen. Por ejemplo la orientación o sentido de la curva puede variar al cambiar de parametrización.

Por ejemplo, dados dos puntos \(A,B\in R^2\) el segmento que une ambos puntos puede ser parametrizado de dos formas equivalentes:

\[(x,y)=tA+(1-t)B\mbox{ con }t\in[0,1]\;\;\;\mbox{ o }\;\;\;(x,y)=tB+(1-t)A\mbox{ con }t\in[0,1]\]

En el primer caso la orientación de la curva es de \(B\) hacia \(A\), mientras que en el segundo es de \(A\) hacia \(B\).

A continuación se definen algunos conceptos importantes sobre curvas parametrizadas

Extremos de una curva:

Dada la curva \(C\) definida por una parametrización \(\vec{r}(t)\) con \(t\in[a,b]\), se llaman extremos de la curva a los puntos \(\vec{r}(a)\) y \(\vec{r}(b)\). La curva se dice cerrada cuando \(\vec{r}(a)=\vec{r}(b)\)

Curva cerrada simple o curva de Jordan:

Una curva cerrada inyectiva salvo en los extremos se dice que es una curva cerrada simple o curva de Jordan. De manera intuitiva, una curva cerrada simple es aquella que no pasa dos veces por el mismo punto salvo en los dos extremos.

En el caso de curvas cerradas simples, se suele considerar que tienen orientación positiva cuando al recorrerlas se deja el interior de la curva a la izquierda. Sería un sentido equivalente al contrario de las agujas del reloj. La siguiente figura muestra los dos tipos de orientación.

---

Ejemplo:

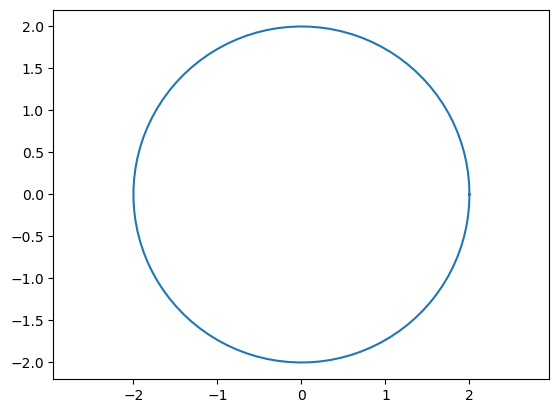
Las ecuaciones paramétricas

\[\begin{split}\begin{array}{l} x=r\cos t\\ y=r\sin t \end{array}\;\;\;\mbox{ con }t\in[0,2\pi]\end{split}\]

corresponden a una circunferencia de centro \((0,0)\) y radio \(r\) recorrida en sentido contrario a las agujas del reloj a partir del punto \((r,0)\) (que corresponde a \(t=0\)). El parámetro \(t\) equivale al ángulo con el eje OX del correspondiente punto, a medida que ese ángulo aumenta se va recorriendo la circunferencia hasta llegar de nuevo al punto de partida. La curva, por tanto, tiene una orientación positiva.

Además, se trata de una curva cerrada simple o curva de Jordan, ya que los únicos puntos en los que \(\vec{r}(t_1)=\vec{r}(t_2)\) son en los dos extremos, \(t_1=0\) y \(t_2=2\pi\).

La ecuación cartesiana correspondiente a esta curva es

\[x^2+y^2=r^2\]

La gráfica de una curva no aporta toda la información sobre cómo se recorre, pues no dice cuantas veces se pasa por cada punto y tampoco caracteriza la orientación o sentido de recorrido. Sin embargo, la parametrización \(\vec{r}(t)\) sí que contiene toda esa información.

t = np.linspace(0,2*np.pi,100)
r = 2
plt.plot(r*np.cos(t), r*np.sin(t))
plt.axis('equal')
plt.show()

Las ecuaciones paramétricas

\[\begin{split}\begin{array}{l} x=r\cos 2t\\ y=r\sin 2t \end{array}\;\;\;\mbox{ con }t\in[0,2\pi]\end{split}\]

definen una curva cerrada cuya representación gráfica sigue siendo la misma que la anterior,pero en este caso la circunferencia es recorrida dos veces.

---

Curvas regulares y vectores tangente a una curva

Una curva se dice de clase \(C^1\) cuando las funciones \(r_i(t)\) que determinan su parametrización \(\vec{r}(t)\) son funciones derivables y con derivada continua en \([a,b]\).

Evidentemente, una curva puede admitir diferentes parametrizaciones equivalentes, pero la condición de ser de clase \(C^1\) es una propiedad intrínseca a la curva, es decir, no depende de la parametrización elegida.

Si las funciones que determinan la parametrización de la curva son diferenciables, se podría calcular el vector

\[\frac{d\vec{r}}{dt}=\vec{r}\,'(t)\]

siendo \(\vec{r}\,'(t)=(r_1'(t),r_2'(t))\) en el caso de curvas en el plano y \(\vec{r}\,'(t)=(r_1'(t),r_2'(t),r_3'(t))\) para las curvas en el espacio.

Este vector tiene una doble interpretación:

• Desde el punto de vista geométrico, el vector \(\vec{r}\,'(t)\) es el vector tangente a la curva \(C\) en el punto \(\vec{r}(t)\).

• Desde el punto de vista físico, el vector \(\vec{r}\,'(t)\) representa el vector velocidad, que es tangente a la trayectoria y está orientado en la dirección del movimiento sobre la curva.

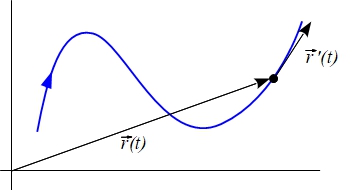
En función de si el vector velocidad en un punto es nulo o no, los puntos de una curva se pueden clasificar en:

• Puntos regulares: cuando \(\vec{r}\,'(t_0)\neq\vec{0}\)

• Puntos singulares: cuando \(\vec{r}\,'(t_0)=\vec{0}\)

Curva regular:

Una curva regular es aquella en la que todos sus puntos son regulares, es decir

\[\vec{r}\,'(t)\neq\vec{0}\;\forall t\in[a,b]\]

Cuando una curva se puede expresar como unión finita de curvas regulares, se dice que es una curva regular a trozos.

La regularidad y la dirección del vector tangente son propiedades intrínsecas de las curvas, que no se ven afectadas por la utilización de otras parametrizaciones equivalentes. Lo que sí podría verse afectado es el sentido del vector tangente.

---

Ejemplo:

Un ejemplo de curva con alguna singularidad es la conocida como cardiode, cuyas ecuaciones paramétricas son:

\[\begin{split}\begin{array}{l} x=\cos t(1+\cos t)\\ y=\sin t(1+\cos t) \end{array}\;\;\;\mbox{ con }t\in[0,2\pi]\end{split}\]

A la vista de su representación gráfica se puede intuir que el \((0,0)\) correspondería a un punto singular.

t = np.linspace(0,2*np.pi,100)
plt.plot(np.cos(t)*(1+np.cos(t)), np.sin(t)*(1+np.cos(t)))
plt.axis('equal')
plt.show()

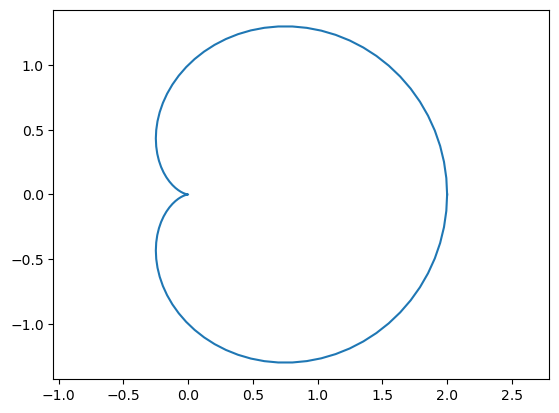
El vector velocidad de la curva podría calcularse con las opciones de derivación simbólica:

x,y,t = sp.symbols('x,y,t')
x = sp.cos(t)*(1+sp.cos(t))
y = sp.sin(t)*(1+sp.cos(t))
velocidad = (sp.diff(x,t), sp.diff(y,t))
velocidad

(-(cos(t) + 1)*sin(t) - sin(t)*cos(t), (cos(t) + 1)*cos(t) - sin(t)**2)

El punto \((0,0)\) corresponde al valor del parámetro \(t=\pi\), y puede comprobarse como en ese punto el vector velocidad es nulo:

print(x.subs({t:np.pi}), y.subs({t:np.pi}))

0 0

---

Dado un punto regular \(\vec{r}(t_0)\) de una curva \(C\), se puede construir su vector tangente unitario

\[\frac{\vec{r}\,'(t_0)}{\|\vec{r}\,'(t_0)\|}\]

y la recta tangente a la curva en ese punto estaría formada por todos los puntos de la forma

\[\vec{r}(t_0)+\lambda \vec{r}\,'(t_0)\;\;\;\forall\lambda\in R\]

En el caso de curvas en el plano, cuando \(r_1'(t_0)\) y \(r_2'(t_0)\) son no nulos, la recta tangente a la curva en el punto \(\vec{r}(t_0)\) podría ser expresada en la forma

\[\frac{x-r_1(t_0)}{r_1'(t_0)}=\frac{y-r_2(t_0)}{r_2'(t_0)}\]

En el caso de curvas en el espacio la recta tangente en el punto \(\vec{r}(t_0)\) vendrá dada por la intersección de dos planos:

\[\begin{split}\begin{array}{l} r_2'(t_0)(x-r_1(t_0))=r_1'(t_0)(y-r_2(t_0))\\ r_3'(t_0)(x-r_1(t_0))=r_1'(t_0)(z-r_3(t_0)) \end{array} \end{split}\]

o lo que es lo mismo, si \(r_1'(t_0)\), \(r_2'(t_0)\), \(r_3'(t_0)\) son no nulos:

\[\frac{x-r_1(t_0)}{r_1'(t_0)}=\frac{y-r_2(t_0)}{r_2'(t_0)}=\frac{z-r_3(t_0)}{r_3'(t_0)}\]

---

Ejemplo:

Dada la curva

\[\begin{split}\begin{array}{l} x=t\\ y=t\sin(t)\\ z=t\cos(t) \end{array}\end{split}\]

con \(t\in[-2\pi,2\pi]\), y el punto \(\vec{r}(\pi)=(\pi,0,-\pi)\), el vector tangente a la curva en dicho punto es

\[\vec{r}'(\pi)=(1,-\pi,-1)\]

y por tanto la recta tangente es

\[\frac{x-\pi}{1}=\frac{y-0}{-\pi}=\frac{z+\pi}{-1}\]

Esa recta tangente puede expresarse en forma paramétrica como:

\[\vec{T}(t)= (\pi,0,-\pi) + \lambda (1,-\pi,-1) = (\pi+\lambda,-\lambda\pi,-\pi-\lambda)\]

A continuación se genera la representación gráfica de la curva junto con la recta tangente el el punto \(\vec{r}(\pi)\).

t = np.linspace(-2*np.pi,2*np.pi,100)
x, y, z = t, t*np.sin(t), t*np.cos(t)
ax = plt.axes(projection='3d')
ax.plot(x,y,z)
L = np.linspace(-1.5,1.5)
ax.plot(np.pi+L, -L*np.pi, -np.pi-L)
ax.scatter(np.pi, 0, -np.pi, c='red')
plt.show()

---

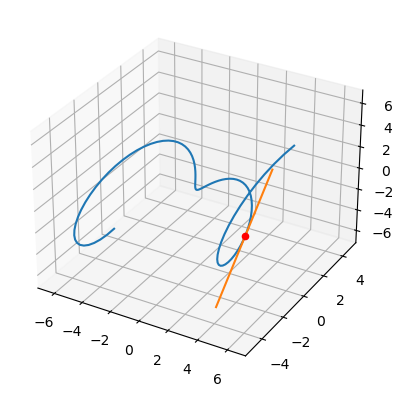
En el caso de curvas definidas mediante intersección de dos superficies

\[\begin{split}\begin{array}{l} g(x,y,z)=0\\ h(x,y,z)=0 \end{array}\end{split}\]

dado un punto \((x_0,y_0,z_0)\) de la curva, los vectores \(\nabla g(x_0,y_0,z_0)\) y \(\nabla h(x_0,y_0,z_0)\) son perpendiculares a las superficies \(g(x,y,z)=0\) y \(h(x,y,z)=0\), respectivamente. En caso de que ambos vectores sean no nulos, el vector

\[\vec{T}= \nabla g(x_0,y_0,z_0) \times \nabla h(x_0,y_0,z_0)\]

sería un vector tangente a la curva en el punto \((x_0,y_0,z_0)\)

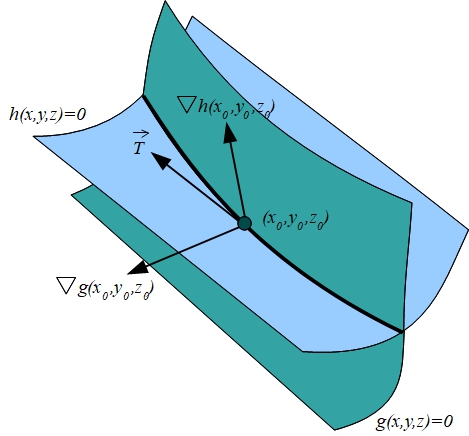
Vector normal a una curva plana

Dado un punto regular \(\vec{r}(t_0)\) de una curva plana, además de la recta tangente puede determinarse la recta normal, es decir, la que corta perpendicularmente a la tangente. Para determinar esa recta se necesita un vector normal. Dada la parametrización \(\vec{r}(t)\) el vector normal unitario en el punto \(\vec{r}(t_0)\) es

\[\vec{n}(t_0)=\frac{(r_2'(t_0),-r_1'(t_0))}{\|\vec{r}\,'(t_0)\|}\]

En el caso de curvas de Jordan, es decir, curvas cerradas simples, con orientación positiva el vector normal es un vector saliente a la curva, tal como puede verse en la siguiente figura

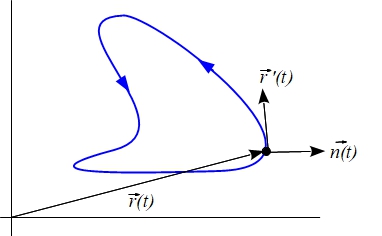
Cuando la curva está definida implícitamente en coordenadas cartesianas \(g(x,y)=0\), el vector gradiente \(\nabla g(x_0,y_0)\) es un vector normal a la curva en el punto \((x_0,y_0)\).

Longitud de una curva regular

Dada una curva regular, su longitud no es más que la suma de los infinitos módulos de los vectores \(\vec{\Delta r}(t)\) cuando el incremento en el parámetro, \(\Delta t\) tiende a 0. En la siguiente figura puede verse la interpretación sobre la curva del vector \(\vec{\Delta r}(t)\).

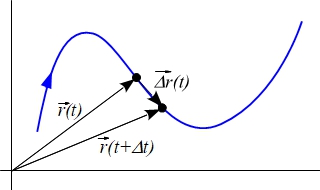
Teniendo en cuenta que

\[\vec{\Delta r}(t)=\frac{\vec{\Delta r}(t)}{\Delta t}\Delta t\]

la suma podría expresarse en la forma

\[\sum_t \frac{\vec{\Delta r}(t)}{\Delta t}\Delta t\]

y cuando \(\Delta t\) tiende a 0 se convierte en la integral que permite calcular la longitud de una curva \(C\) que viene determinada por una parametrización \(\vec{r}(t)\) con \(t\in[a,b]\):

\[L_C= \int_a^b \|\frac{d\vec{r}(t)}{dt}\|dt= \int_a^b \|\vec{r}\,'(t)\|dt \]

Es decir, la longitud puede verse como la integral del módulo de la velocidad.

La longitud de una curva es una propiedad intrínseca, por tanto no se ve afectada por el uso de parametrizaciones equivalentes.

Como caso particular de curvas planas que vienen dadas por coordenadas cartesianas explícitas \(y=f(x)\), la longitud de la curva con \(x\in[a,b]\) está dada por

\[L_C=\int_a^b\sqrt{1+f'(x)^2}dx\]

---

Ejemplo:

La curva definida por

\[\begin{split}\begin{array}{rl} C:[0,4\pi] &\longrightarrow R^2\\ t &\longrightarrow \vec{r}(t)=(e^{-t/5}\cos t,e^{-t/5}\sin t) \end{array}\end{split}\]

es un caso particular de una curva regular conocida como espiral logarítmica. La representación gráfica asociada puede generarse fácilmente con Python:

t = np.linspace(0,4*np.pi,100)
plt.plot(np.exp(-t/5)*np.cos(t), np.exp(-t/5)*np.sin(t))
plt.show()

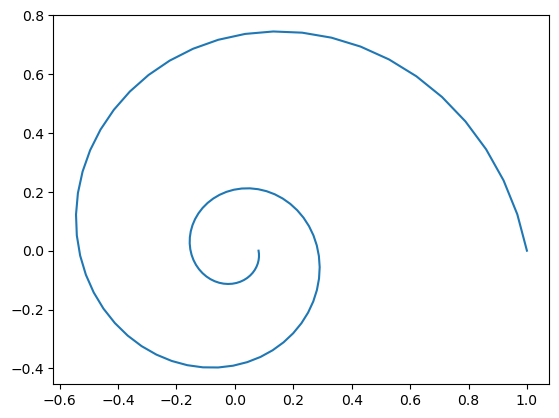
El vector velocidad de esta curva, o equivalentemente, el vector tangente sería

\[ \vec{r}\,'(t)=\left( -\frac{1}{5}e^{-t/5}\cos t - e^{-t/5}\sin t , -\frac{1}{5}e^{-t/5}\sin t + e^{-t/5}\cos t \right) \]

y su módulo

\[\|\vec{r}\,'(t)\| = \sqrt{\left(-\frac{1}{5}e^{-t/5}\cos t - e^{-t/5}\sin t\right)^2+\left(-\frac{1}{5}e^{-t/5}\sin t + e^{-t/5}\cos t\right)^2}\]

\[ = \frac{\sqrt{26}}{5}e^{-t/5}\]

La longitud de la curva se calcularía mediante la integral

\[ L_C=\int_0^{4\pi} \frac{\sqrt{26}}{5}e^{-t/5} dt = \left. -\sqrt{26}e^{-t/5} \right|_0^{4\pi}= -\sqrt{26}e^{-4\pi/5}+\sqrt{26}=4.686 \]

El cálculo de longitudes de curvas en Python podría hacerse de dos maneras, la primera es mediante la definición de un objeto de tipo curva y el uso de la propiedad length que ofrece el paquete SymPy

import sympy as sp
from sympy.geometry import Curve
t = sp.symbols('t')
espiral = Curve((sp.exp(-t/5)*sp.cos(t), sp.exp(-t/5)*sp.sin(t)), (t, 0, 4*sp.pi))
espiral.length

\[\displaystyle - \frac{\sqrt{26}}{e^{\frac{4 \pi}{5}}} + \sqrt{26}\]

espiral.length.evalf()

\[\displaystyle 4.68598571552783\]

La otra opción sería el cálculo directamente de la integral

x,y,t = sp.symbols('x,y,t')
x,y = sp.exp(-t/5)*sp.cos(t), sp.exp(-t/5)*sp.sin(t)
mv = sp.sqrt(sp.diff(x,t)**2+sp.diff(y,t)**2)
sp.integrate(mv, (t,0,4*sp.pi))

\[\displaystyle - \frac{\sqrt{26}}{e^{\frac{4 \pi}{5}}} + \sqrt{26}\]

---

No siempre es posible realizar los procesos de integración de manera simbólica y en tales casos debe recurrirse a un proceso de aproximación numérica de la integral que calcula la longitud. A continuación se muestra un ejemplo que pone esto de manifiesto.

---

Ejemplo:

La longitud de la curva en el espacio parametrizada por \(\vec{r}(t)=(\log t, \sin t, t\cos t)\) con \(t\in[1,20]\) resulta imposible de calcular con las funciones que ofrece el paquete Sympy. De entrada, al ser tridimensional no es posible definir un objeto Curve pero además la integración simbólica del módulo del vector velocidad no es posible

x,y,z,t = sp.symbols('x,y,z,t')
x,y,z = sp.log(t), sp.sin(t), t*sp.cos(t)
mv = sp.sqrt(sp.diff(x,t)**2+sp.diff(y,t)**2+sp.diff(z,t)**2)
sp.integrate(mv, (t,1,20))

\[\displaystyle \int\limits_{1}^{20} \frac{\sqrt{t^{4} \sin^{2}{\left(t \right)} - 2 t^{3} \sin{\left(t \right)} \cos{\left(t \right)} + 2 t^{2} \cos^{2}{\left(t \right)} + 1}}{t}\, dt\]

En este caso no queda más remedio que recurrir a la integración numérica con el paquete SciPy. Al ser la integral definida a aproximar una integral simple (una sola variable) la función que se tiene que utilizar es quad

mv.simplify()

\[\displaystyle \sqrt{\left(t \sin{\left(t \right)} - \cos{\left(t \right)}\right)^{2} + \cos^{2}{\left(t \right)} + \frac{1}{t^{2}}}\]

import numpy as np
from scipy import integrate
f = lambda t: np.sqrt( (t*np.sin(t)-np.cos(t))**2 + np.cos(t)**2 + 1/t**2 )
integrate.quad(f, np.pi, 2*np.pi)

(10.294663180778054, 1.3918403905549982e-07)

Ejercicios propuestos

• Calcular los vectores tangente y normal a la curva parametrizada por \(\vec{r}(t)=(t^2,-t)\) en el punto correspondiente a \(\vec{r}(1)\).

• Determinar los valores de \(t\) para los cuales la siguiente curva tiene tangente horizontal, tiene tangente vertical o no es regular.

\[\vec{r}(t)=(2t^3-3t^2,t-2\arctan t)\]

• Obtener una parametrización de las siguientes curvas y calcular en cada caso el vector tangente unitario y el vector normal.

\[\begin{split} \begin{array}{l} C_1:\; y=x^2+3x \\ C_2:\; x^2+y^2+2y=0 \end{array} \end{split}\]

• Calcular la longitud de la curva \(C\) definida por

\[\begin{split} \begin{array}{rl} C:[1,3] &\longrightarrow R^2\\ t &\longrightarrow \vec{r}(t)=\left(2t-t^2,\frac{8}{3}t^{3/2}\right) \end{array} \end{split}\]

• Calcular la longitud de la curva \(C\) definida por

\[\begin{split}\begin{array}{rl} C:[0,4] &\longrightarrow R^2\\ t &\longrightarrow \vec{r}(t)=(t^3,t^2) \end{array} \end{split}\]

• Dada la curva definida por \(\vec{r}(t)=(e^t\cos t,e^t\sin t,e^t)\), comprobar que se encuentra contenida en el cono \(x^2+y^2=z^2\) y calcular la ecuación de la recta tangente a la curva en un punto \(\vec{r}(t_0)\).