Ecuaciones diferenciales separables y reducibles a separables#

Ecuaciones separables:

Una ecuación diferencial se dice separable cuando puede expresarse en la forma

\[\frac{dy}{dx}=f(x)g(y)\]

El proceso de resolución de una ecuación separable consiste en separar las dos variables en lados opuestos de la ecuación y realizar una doble integración, a un lado en la variable independiente \(x\) y al otro en la dependiente \(y\), incluyendo además una constante de integración. Es decir

\[\int \frac{dy}{g(y)}=\int f(x)dx + C\]

Ejemplo:

Dada la ecuación

\[\frac{dy}{dx}+(\sin x)y=0\]

se podría expresar en la forma

\[\frac{dy}{y}=-(\sin x)dx\]

y por tanto

\[\int\frac{dy}{y}=\int-(\sin x)dx + C\]

de donde se obtiene la solución general:

\[\log y=\cos x + C\Rightarrow y=e^{\cos x+C}=Ke^{\cos x}\]

Esa misma ecuación puede resolverse simbólicamente con Python.

import sympy as sp
x = sp.Symbol('x')
y = sp.Function('y')
ecuacion = sp.Eq(y(x).diff(x)+sp.sin(x)*y(x), 0)
sp.dsolve(ecuacion)
\[\displaystyle y{\left(x \right)} = C_{1} e^{\cos{\left(x \right)}}\]

En el proceso de resolución se pueden perder soluciones con las manipulaciones algebraicas de la ecuación. Por ello, debe comprobarse si existe alguna otra solución singular y añadirla para la obtención de la solución general.

En el ejemplo anterior, al separar las variables se está haciendo la suposición de que \(y\neq 0\), pero la función constante \(y=0\) también verifica la ecuación. En este caso, esa solución ya está incluida en la familia paramétrica de soluciones obtenida, en concreto corresponde a la solución con \(K=0\). Hay otros casos en los que estas soluciones singulares no quedan incluidas en la familia paramétrica, y por tanto hay que también considerarlas.

Ejemplo:

La ecuación

\[\frac{dy}{dx}+3x^2y^2=0\]

puede expresarse como

\[-\frac{dy}{y^2}=3x^2dx\]

Pero de nuevo se está asumiendo que \(y\neq 0\). Haciendo una doble integración se obtiene la familia paramétrica de soluciones:

\[\int-\frac{dy}{y^2}=\int 3x^2dx \Rightarrow \frac{1}{y}=x^3+C\]

o equivalentemente:

\[y=\frac{1}{x^3+C}\]

Ahora bien, la solución \(y=0\) también verifica la ecuación y no está incluida en esa familia, es decir, no corresponde a ningún valor de la constante \(C\), por tanto la solución general de la ecuación es

\[y=\frac{1}{x^3+C},\;\;\;\;\;\;y=0\]

Esas soluciones especiales no siempre son correctamente identificadas por Python, por ejemplo al resolver esta ecuación con dsolve() no se obtiene la solución \(y=0\).

ecuacion = sp.Eq(y(x).diff(x) + 3*x**2*y(x)**2, 0)
sp.dsolve(ecuacion)
\[\displaystyle y{\left(x \right)} = \frac{1}{C_{1} + x^{3}}\]

Ejemplo: seguidores de una red social

Supóngase que el número de seguidores de una cuenta en una red social crece de manera proporcional al número de seguidores que posee. Esto significa que, si \(S(t)\) es una función que determina el número de seguidores de dicha cuenta en el instante de tiempo \(t\) (donde \(t\) se mide en días), entonces la tasa de crecimiento de seguidores (\(dS/dt\)) es un cierto múltiplo \(k\) del número de seguidores, es decir, se tiene la siguiente ecuación diferencial:

\[\frac{dS}{dt}=kS(t)\]

Se trata de una ecuación separable que puede ser resuelta fácilmente con una doble integración. La solución general es

\[S(t)=C e^{kt}\]

donde \(C\) es una constante arbitraria y \(k\) la constante de proporcionalidad en la ecuación.

t, k = sp.symbols('t,k')
S = sp.Function('S')
ecuacion = sp.Eq(S(t).diff(t), k*(S(t)))
sp.dsolve(ecuacion)
\[\displaystyle S{\left(t \right)} = C_{1} e^{k t}\]

Si se desean determinar los valores de esas dos constantes se necesitaría alguna información adicional. Por ejemplo, si se sabe que el número de seguidores en el instante inicial (\(t=0\)) es de 200, y al cabo de una semana (instante \(t=7\)) se tienen ya 350 seguidores, se podría determinar fácilmente el valor de ambas constantes planteando el sistema de ecuaciones:

\[\begin{split}\left\{\begin{array}{l} S(0)=C=200 \\ S(7)=c e^{7k}=350 \end{array}\right.\end{split}\]

Tanto la generación de esas ecuaciones como su resolución puede hacerse con funciones del paquete SymPy. La resolución de ecuaciones (no diferenciales) se realiza con la función solve().

sp.dsolve(ecuacion).subs(t,0).subs(S(0),200)
\[\displaystyle 200 = C_{1}\]
sp.dsolve(ecuacion).subs(t,7).subs(S(7),350)
\[\displaystyle 350 = C_{1} e^{7 k}\]
C1, k = sp.symbols('C1,k')
sol = sp.solve((sp.dsolve(ecuacion).subs(t,0).subs(S(0),200),
                sp.dsolve(ecuacion).subs(t,7).subs(S(7),350)),(C1,k))
sol

[(200, -2*log(2)/7 + log(7)/7),
 (200, -log(2) + log(224)/7 - 2*I*pi/7),
 (200, -log(2) + log(224)/7 + 2*I*pi/7),
 (200, -log(2) + log(224)/7 + log(-sin(pi/14) - I*cos(pi/14))),
 (200, -log(2) + log(224)/7 + log(-sin(pi/14) + I*cos(pi/14))),
 (200, -log(2) + log(224)/7 + log(-exp(-I*pi/7))),
 (200, -log(2) + log(224)/7 + log(-exp(I*pi/7)))]

sol[0][1].evalf()
\[\displaystyle 0.0799451125622032\]

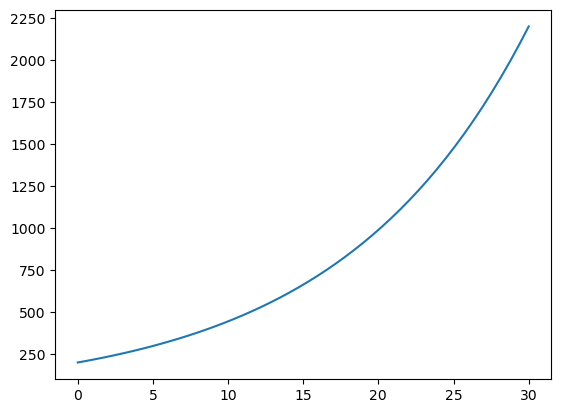
De todas las soluciones de ese sistema de ecuaciones, solo interesa la que corresponde a valores reales. Teniendo en cuenta esto, la función que permitiría predecir la evolución del número de seguidores es:

\[S(t)=200 e^{0.077945t}\]

cuya gráfica mostraría un crecimiento exponencial en el número de seguidores:

import matplotlib.pyplot as plt
import numpy as np
tiempo = np.linspace(0,30)
s = 200*np.exp(0.079945*tiempo)
plt.plot(tiempo, s)
plt.show()
_images/fe5a6fc23950dd2801a006498eef59afe01ce8025f41b21f1f73ece1b7fe1bcf.png

Ecuaciones reducibles a separables#

Existen ecuaciones que no son directamente separables pero que sí que se pueden convertir en separables con un pequeño cambio de variable. El primer caso es el de las ecuaciones del tipo

\[ \frac{dy}{dx}=f(ax+by)\]

Estas ecuaciones se reducen a separables con el cambio \(z=ax+by\).

Ejemplo:

La ecuación

\[y'-e^xe^y=-1\]

se puede expresar en la forma:

\[\frac{dy}{dx}=e^{x+y}-1\]

Si se aplica el cambio \(z=x+y\) se obtiene

\[\frac{d}{dx}(z-x)=e^z-1\Rightarrow \frac{dz}{dx}-1=e^z-1\Rightarrow \frac{dz}{dx}=e^z\]

Esta última ecuación ya es separable, y su solución es:

\[e^{-z}dz=dx\Rightarrow -e^{-z}=x+C\]

Deshaciendo el cambio se obtiene la solución de la ecuación inicial:

\[e^{-x-y}=-x-C \Rightarrow y=-x-\log(C-x)\]

siendo \(C\) una constante arbitraria.

ecuacion = sp.Eq(y(x).diff(x) - sp.exp(x)*sp.exp(y(x)), -1)
sp.dsolve(ecuacion)
\[\displaystyle y{\left(x \right)} = \log{\left(\frac{e^{- x}}{C_{1} - x} \right)}\]

Ecuaciones homogéneas#

También son reducibles a separables las ecuaciones denominadas homogéneas, que son las que se pueden expresar en la forma

\[\frac{dy}{dx}=f\left(\frac{y}{x}\right)\]

Si se considera \(F(x,y)=f(y/x)\), se cumpliría que dicha función es homogénea de grado 0. En general, una función \(F(x,y)\) es homogénea de grado \(n\) cuando verifica

\[F(\lambda x,\lambda y)=\lambda^nF(x,y)\]

Cuando se tiene una ecuación de la forma

\[\frac{dy}{dx}=F(x,y)\]

siendo \(F(x,y)\) una función homogénea de grado \(0\), con el cambio de variable \(z=y/x\), o equivalentemente \(y=zx\), la ecuación se convierte en una ecuación de variables separables.

Ejemplo:

La ecuación

\[\frac{dy}{dx}=\frac{x^2+y^2}{xy}\]

viene definida por una función homogénea de grado 0. Si se realiza el cambio \(z=y/x\), entonces

\[y=zx\Rightarrow \frac{dy}{dx}=\frac{d}{dx}(zx)=\frac{dz}{dx}x+z\]

Esto llevado a la ecuación diferencial conduce a

\[\frac{dz}{dx}x+z = \frac{x^2+z^2x^2}{zx^2}=\frac{1+z^2}{z}\]

Por tanto

\[\frac{dz}{dx}x=\frac{1+z^2}{z}-z=\frac{1}{z}\]

que ya es una ecuación separable. Separando las variables se obtiene

\[z\,dz=\frac{dx}{x}\Rightarrow \int z\,dz=\int\frac{dx}{x}\Rightarrow \frac{z^2}{2}=\log x + c\]

Deshaciendo el cambio se obtiene la solución de la ecuación inicial definida implícitamente:

\[\frac{y^2}{2x^2}=\log x + c\]
ecuacion = sp.Eq(y(x).diff(x), (x**2+y(x)**2)/(x*y(x)))
sp.dsolve(ecuacion)

[Eq(y(x), -x*sqrt(C1 + 2*log(x))), Eq(y(x), x*sqrt(C1 + 2*log(x)))]

Finalmente son reducibles a homogéneas las ecuaciones que se pueden expresar en la forma

\[\frac{dy}{dx}=f\left(\frac{a_1x+b_1y+c_1}{a_2x+b_2y+c_2}\right)\]

En este caso, para convertirlas en homogéneas hay que distinguir dos casos:

  • Si las rectas \(a_1x+b_1y+c_1=0\) y \(a_2x+b_2y+c_2=0\) se cortan en un punto \((x_0,y_0)\), con los cambios \(u=x-x_0\) y \(v=y-y_0\), la ecuación se reduce a homogénea.

  • Si las rectas \(a_1x+b_1y+c_1=0\) y \(a_2x+b_2y+c_2=0\) son paralelas, con el cambio \(z=a_1x+b_1y\) la ecuación se reduce a homogénea.

Ejemplo:

Dada la ecuación

\[\frac{dy}{dx}=\frac{3x+y-2}{x-1}\]

las rectas \(3x+y-2=0\) y \(x-1=0\) se cortan en el punto \((1,-1)\). Entonces, el cambio que reduce la ecuación a homogénea es:

\[u=x-1,\;\;\;\;v=y+1\]

y el cambio inverso sería \(x=u+1\) e \(y=v-1\). Aplicando la regla de la cadena, en este caso se cumpliría

\[\frac{dy}{dx}=\frac{dy}{dv}\frac{dv}{du}\frac{du}{dx}=1\frac{dv}{du}1=\frac{dv}{du}\]

Entonces la ecuación original quedaría expresada como

\[\frac{dv}{du}=\frac{3(u+1)+(v-1)-2}{(u+1)-1}=\frac{3u+v}{u}=\frac{v}{u}+3\]

que ya es una ecuación homogénea. Esta última ecuación necesita un cambio adicional para convertirse en separable, el cambio a aplicar es \(z=v/u\), y la ecuación resultante:

\[\frac{dz}{du}u+z=z+3\Rightarrow dz=3\frac{du}{u}\]

Integrando a ambos lados y deshaciendo los cambios se obtiene:

\[z=3\log|u|+C\Rightarrow v=u(3\log|u|+C)\]
\[y=(x-1)(3\log|x-1|+C)-1\]
ecuacion = sp.Eq(y(x).diff(x), (3*x+y(x)-2)/(x-1))
sp.dsolve(ecuacion)
\[\displaystyle y{\left(x \right)} = C_{1} x - C_{1} + 3 x \log{\left(x - 1 \right)} - 3 \log{\left(x - 1 \right)} - 1\]

Ejercicios propuestos#

  • Resolver las siguientes ecuaciones separables:

\[\frac{dy}{dx}=\frac{x+2}{y^4}\]
\[y^2\frac{dy}{dx}=e^x\]
\[\frac{dy}{dx}=\frac{y+3}{2x+1}\]

  • Resolver el siguiente problema de valor inicial

\[\begin{split}\left\{ \begin{array}{l} \frac{dy}{dx}=\frac{y(2x^2+1)}{x}\\ y(1)=1 \end{array} \right. \end{split}\]

  • Resolver la siguiente ecuación homogénea

\[\frac{dy}{dx}=\frac{y\sin(y/x)+x}{x\sin(y/x)}\]

  • Aplicar un cambio de variable \(z=x-y\) para convertir en separable y resolver la siguiente ecuación diferencial

\[\frac{dy}{dx}=\frac{x-y}{x-y+2}\]

  • Calcular la solución general de las siguientes ecuaciones reducibles a homogéneas

\[\frac{dy}{dx}=\frac{2x+3y-1}{4x+6y}\]
\[\frac{dy}{dx}=\frac{x+y-1}{x+4y+2}\]