Campos conservativos: independencia del camino#
En general, la integral curvilínea de un campo vectorial sobre una curva que conecta dos puntos depende de la trayectoria de dicha curva, es decir, del camino seguido para ir de un punto a otro. Una primera pregunta que puede surgir a raíz de este hecho es saber si en algunas circunstancias la circulación de un campo vectorial, es decir, la integral curvilínea, es independiente del camino seguido para moverse entre los dos puntos. Los campos vectoriales que cumplen esta propiedad recibirán un nombre especial: campos conservativos.
De entrada, por supuesto, no todos los campos van a ser conservativos. De hecho lo más probable es que en un campo la integral de línea dependa de la trayectoria seguida. Sin embargo, sí que existen campos en los que la trayectoria no importa, lo que importa son los puntos de inicio y finalización. A continuación se muestra un ejemplo particular de campo vectorial que cumple esta característica.
Ejemplo:
Dado el campo \(\vec{F}(x,y)=(2x+y^2)\vec{i}+2xy\vec{j}\) sobre el que se plantea seguir una trayectoria entre los puntos \((1,0)\) y \((0,1)\). Evidentemente, son infinitas las posibles trayectorias a seguir, pero se considerarán dos alternativas:
Curva \(C_1\): arco de la circunferencia de centro \((0,0)\) y radio \(1\), partiendo del punto \((1,0)\) y llegando al punto \((0,1)\).
Curva \(C_2\): formada por dos segmentos consecutivos, el primero desde el punto \((1,0)\) al punto \((0,0)\), y el segundo desde \((0,0)\) a \((0,1)\)
En primer lugar se necesitaría parametrizar ambas trayectorias.
Una parametrización de la curva \(C_1\) podría ser:
Para parametrizar la trayectoria \(C_2\) conviene dividirla en dos, por un lado el segmento \(S_1\) que va desde el punto \((1,0)\) al punto \((0,0)\), y posteriormente el segundo segmento \(S_2\), desde \((0,0)\) a \((0,1)\). Las parametrizaciones de ambos segmentos serían
A continuación puede realizarse la representación del campo junto con las dos posibles trayectorias.
import numpy as np
import matplotlib.pyplot as plt
x,y = np.meshgrid(np.linspace(0,1,10),np.linspace(0,1,10))
u, v = 2*x+y**2, 2*x*y
plt.quiver(x,y,u,v)
t = np.linspace(0,np.pi/2)
rx, ry = np.cos(t), np.sin(t)
plt.plot(rx,ry, linewidth=4)
plt.text(rx[0], ry[0], 'Inicio', bbox=dict(facecolor='blue', alpha=0.5))
plt.text(rx[-1], ry[-1], 'Final', bbox=dict(facecolor='red', alpha=0.5))
t = np.linspace(0,1)
rx, ry = 1-t, np.zeros_like(t)
plt.plot(rx,ry, linewidth=4, c='red')
rx, ry = np.zeros_like(t), t
plt.plot(rx,ry, linewidth=4, c='red')
plt.show()
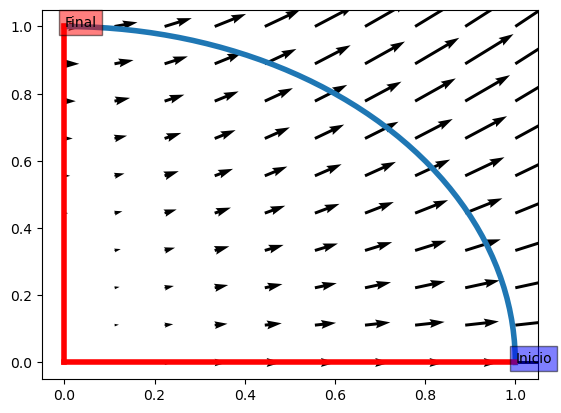
Una vez obtenidas las parametrizaciones, la integral de línea del campo sobre la curva \(C_1\) sería:
Con un cambio de variable \(u=\cos t\), la integral anterior es:
En el caso de la trayectoria \(C_2\), la integral curvilínea podría dividirse en dos:
Calculando ambas integrales por separado, se obtiene:
El cálculo de esta segunda integral podría haberse evitado si se tiene en cuenta que el campo vectorial es ortogonal al segmento \(S_2\), por lo que la integral del campo sobre ese segmento debe ser nula.
Todas estas integrales de línea podrían ser calculadas fácilmente con las funciones de integración vectorial simbólica del módulo Vector de Python.
import sympy as sp
import sympy.vector as vec
from sympy.geometry import Curve
# establecimiento del sistema de coordenadas
S = vec.CoordSys3D('')
# definición del campo
F = (2*S.x + S.y**2)*S.i + 2*S.x*S.y*S.j
# definición de las curvas
t = sp.symbols('t')
C1 = Curve((sp.cos(t), sp.sin(t)), (t, 0, sp.pi/2))
S1 = Curve((1-t, 0), (t, 0, 1))
S2 = Curve((0, t), (t, 0, 1))
# cálculo de las integrales de línea
I1 = vec.vector_integrate(F, C1)
I2 = vec.vector_integrate(F, S1)
I3 = vec.vector_integrate(F, S2)
print('Integral a lo largo de la trayectoria C1:', I1)
print('Integral a lo largo de la trayectoria C2:', I2+I3)
Integral a lo largo de la trayectoria C1: -1
Integral a lo largo de la trayectoria C2: -1
En definitiva, se obtiene
En este caso concreto la integral de línea no depende de la trayectoria elegida para ir del punto \((1,0)\) al \((0,1)\), además el campo se opone al movimiento (integral negativa).
Se podría comprobar que el valor de la integral seguiría siendo el mismo para cualquier otra trayectoria que una esos puntos- Incluso, para cualquier otra pareja de puntos del campo que se considere, la integral de línea no dependería del camino seguido para unir dichos puntos.
A la vista de este ejemplo, se puede deducir también que si se considera un camino cerrado \(C_0\) que se inicia en el punto \((1,0)\), se desplaza al punto \((0,1)\) por la curva \(C_2\), y regresa al punto \((1,0)\) por la curva \(-C_1\) (misma trayectoria que \(C_1\) pero recorrida en sentido contrario), la integral a lo largo de ese camino cerrado sería nula, ya que
Esa sería igualmente una característica de este campo, la integral sobre cualquier curva cerrada es siempre nula.
Las características que se cumplen en el campo del ejemplo anterior no son cumplidas por cualquier tipo de campo vectorial, de hecho hay campos en los que la integral sí que depende del camino y en los que existen integrales no nulas sobre curvas cerradas. A continuación se muestra un ejemplo.
Ejemplo:
En el campo vectorial \(\vec{F}(x,y)=-y\vec{i}+x\vec{j}\) si se considera la curva cerrada \(C\) formada por la circunferencia de centro el origen y radio 1, se puede comprobar que:
F = -S.y*S.i + S.x*S.j
t = sp.symbols('t')
C = Curve((sp.cos(t), sp.sin(t)), (t, 0, 2*sp.pi))
vec.vector_integrate(F, C)
En ese mismo campo, si se consideran dos trayectorias distintas para ir del \((0,0)\) al \((1,1)\), la primera a través de la parábola \((t,t^2)\) con \(t\in[0,1]\), y la segunda a través de la parábola \((t^2,t)\) con \(t\in[0,1]\), las integrales correspondientes serían:
con lo que se comprueba que la integral también depende del camino elegido.
vec.vector_integrate(F, Curve((t, t**2), (t, 0, 1)))
vec.vector_integrate(F, Curve((t**2, t), (t, 0, 1)))
En definitiva, no todos los campos cumplen la característica de independencia del camino, de manera que a los que lo cumplan se les llamará campos conservativos.
Campo conservativo:
Dado un conjunto abierto conexo \(\Omega\subset R^n\) un campo vectorial continuo \(\vec{F}:\Omega\longrightarrow R^n\) se dice conservativo cuando la circulación (integral curvilínea) entre dos puntos cualesquiera de \(\Omega\) es independiente del camino (de clase \(C^1\) a trozos) que los una.
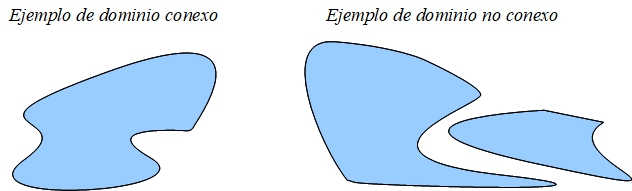
En esta definición se exige que el dominio del campo vectorial sea un conjunto conexo para que dos puntos cualesquiera de \(\Omega\) siempre puedan ser unidos por un camino contenido en \(\Omega\). En la siguiente figura se muestra un ejemplo de conjunto conexo y otro de conjunto no conexo en \(R^2\), en el segundo es posible encontrar puntos que no pueden unirse por caminos continuos contenidos dentro del conjunto.
Puede comprobarse que la característica de independencia de camino es totalmente equivalente a la de que la circulación sobre cualquier camino cerrado sea nula.
Campos gradiente y funciones potenciales#
Cuando se presentó el concepto de campo vectorial se mostraron algunos campos especiales que surgen al aplicar determinados operadores diferenciales. Entre ellos destaca por su importancia el campo gradiente. Dado un campo escalar diferenciable su campo gradiente \(\nabla f\) es el campo que se construye a partir de las derivadas parciales de la función del campo.
Funciones potenciales:
Dado un campo gradiente \(\nabla f\), a la función \(f\) se la denomina función potencial del campo o potencial escalar.
Con esta definición, se dice que un campo vectorial \(\vec{F}\) es un campo gradiente cuando tiene una función potencial escalar \(f\), es decir, \(\vec{F}=\nabla f\). Así por ejemplo, los campos gravitacionales o eléctricos son campos gradientes de determinadas funciones potenciales.
Teniendo en cuenta que dos funciones que se diferencian en una constante tienen las mismas derivadas, un campo gradiente tiene infinitas funciones potenciales posibles, todas ellas diferenciándose en una constante.
Debe advertirse que en Física se suele adoptar como definición de potencial escalar de un campo \(\vec{F}\) la función \(U\) tal que \(\vec{F}=-\nabla U\).
Los campos gradiente satisfacen una propiedad muy interesante, que en cierta forma generaliza el teorema fundamental del cálculo integral, y que viene establecida por el siguiente teorema.
Teorema fundamental del cálculo para integrales de línea:
Dado un campo gradiente \(\nabla f\) y una curva \(C\) con extremos en los puntos \(P_0\) y \(P_1\), entonces
Por ejemplo, en el caso de curvas en el plano, si la curva \(C\) viene parametrizada por \(\vec{r}(t)=(x(t),y(t))\) con \(t\in[t_0,t_1]\), siendo \(\vec{r}(t_0)=P_0\) y \(\vec{r}(t_1)=P_1\), entonces
Ejemplo:
El campo \(\vec{F}(x,y)=(2x+y^2)\vec{i}+2xy\vec{j}\) analizado anteriormente, es realmente un campo gradiente, siendo una función potencial
por tanto, el cálculo de la integrales curvilíneas vistas en el ejemplo puede simplificarse notablemente:
El módulo Vector del paquete SymPy ofrece la posibilidad de encontrar funciones potenciales para aquellos campos que las acepten. Además dispone de una función para evaluar directamente la diferencia de potenciales entre los dos puntos. Esa función es scalar_potential_difference() y recibe como argumentos el campo, el sistema de coordenadas y los puntos de inicio y finalización.
F = (2*S.x + S.y**2)*S.i + 2*S.x*S.y*S.j
vec.scalar_potential(F, S)
Los puntos se deben definir a partir del origen de coordenadas del sistema de referencia usando la función locate_new():
inicio = S.origin.locate_new('', S.i) # definición del punto (1,0)
final = S.origin.locate_new('', S.j) # definición del punto (0,1)
vec.scalar_potential_difference(F, S, inicio, final)
Como consecuencia del Teorema Fundamental del Cálculo de Integrales de Línea se podría decir que los campos gradientes \(\vec{F}=\nabla f\) cumplen las siguientes características:
Dadas dos curvas \(C_1\) y \(C_2\) con extremos en \(P_0\) y \(P_1\)
Si \(C\) es una curva cerrada
En definitiva, todo campo gradiente es conservativo.
Desde un punto de vista físico, en los campos conservativos el trabajo realizado por el campo de fuerzas es el cambio en los valores de la función potencial. Por ejemplo, en un campo eléctrico, el trabajo representa el cambio en los potenciales eléctricos (voltajes). El hecho de que el campo sea conservativo significa que no se puede extraer libremente energía del campo en el movimiento a lo largo de una trayectoria cerrada, es decir, campo conservativo implica conservación de la energía. Si un campo de fuerzas es conservativo, la suma de las energías cinética y potencial de una partícula que se desplaza es constante.
Los campos conservativos tienen, por tanto, interesantes propiedades desde el punto de vista físico, por lo que interesa identificar rasgos que permitan decidir si un campo es o no conservativo. A continuación se enuncian 4 propiedades equivalentes para saber cuando un campo \(\vec{F}(x,y)=M(x,y)\vec{i}+N(x,y)\vec{j}\) es conservativo:
La integral de línea sobre cualquier curva cerrada es nula
La integral de línea es independiente del camino seguido entre los extremos de la curva.
El campo \(\vec{F}\) es un campo gradiente para alguna función potencial, es decir, \(\vec{F}=\nabla f\).
\(M(x,y)dx+N(x,y)dy\) es una diferencial exacta, es decir, \(M(x,y)dx+N(x,y)dy=df\) para una función \(f(x,y)\).
Las propiedades anteriores siguen siendo válidas para campos conservativos tridimensionales.
Ejemplo:
Se comprueba a continuación, usando las posibilidades del paquete SymPy, que el campo
es conservativo
campoConservativo = 4*S.x*S.y*S.i + 2*S.x**2*S.j + 4*S.k
print(campoConservativo)
vec.is_conservative(campoConservativo)
4*.x*.y*.i + 2*.x**2*.j + 4*.k
True
Una función potencial sería:
vec.scalar_potential(campoConservativo, S)
Al ser conservativo, el trabajo ejercido por el campo no depende de la trayectoria seguida en el movimiento, únicamente depende del punto de inicio y de finalización del desplazamiento. Ese trabajo, correspondiente a la integral de línea, puede calcularse directamente evaluando la diferencia de potenciales entre los dos puntos. Por ejemplo, si se desea calcular el trabajo em un desplazamiento del punto \((1,1,1)\) al punto \((2,0,6)\), se podría realizar obteniendo la diferencia de potenciales
inicio = S.origin.locate_new('', S.i + S.j + S.k)
final = S.origin.locate_new('', 2*S.i + 6*S.k)
vec.scalar_potential_difference(campoConservativo, S, inicio, final)
Identificación de campos conservativos y obtención de funciones potenciales#
En la sección anterior se ha visto que campos conservativos y campos gradiente son conceptos equivalentes. Además de las propiedades enunciadas en la sección anterior, interesa disponer de algún test de fácil aplicación que permita:
Reconocer si un campo es conservativo.
Encontrar una función potencial en caso de que lo sea.
A continuación se enuncia una condición necesaria para que un campo plano sea conservativo:
Condición necesaria para ser campo conservativo:
Dado un campo vectorial \(\vec{F}(x,y)=M(x,y)\vec{i}+N(x,y)\vec{j}\) diferenciable, si \(\vec{F}\) es un campo conservativo, entonces necesariamente:
Esta característica es fácil de comprobar, ya que si \(\vec{F}\) es un campo conservativo, será el campo gradiente de una determinada función potencial \(f(x,y)\), entonces
y por tanto
Ejemplo:
En el campo \(\vec{F}(x,y)=(2x+y^2)\vec{i}+2xy\vec{j}\) analizado anteriormente, la condición necesaria para ser conservativo evidentemente se cumple:
Sin embargo, esa condición necesaria no es una condición suficiente para asegurar que el campo sea conservativo; se requeriría exigir algo más al campo vectorial. En el siguiente ejemplo se muestra un campo vectorial que aún cumpliendo \(\frac{\partial M}{\partial y}=\frac{\partial N}{\partial x}\) no es conservativo.
Ejemplo:
El campo
cumple la condición
sin embargo no es un campo conservativo, ya que, por ejemplo, la integral a lo largo de la curva cerrada \(C\) formada por la circunferencia de centro \((0,0)\) y radio 1, no es nula.
La parametrización de dicha curva cerrada es \(\vec{r}(t)=(\cos t,\sin t)\) con \(t\in[0,2\pi]\), y la integral valdría:
En definitiva, este campo no puede ser conservativo. Si se observa, el campo \(\vec{F}\) tiene una característica especial, en su dominio de definición no se encuentra el punto \((0,0)\).
Se ha visto que la igualdad de derivadas cruzadas no es suficiente para que un campo en el plano sea conservativo. Sin embargo, si al dominio del campo se el ponen condiciones adicionales, entonces la igualdad de derivadas cruzadas es también una condición suficiente para que el campo sea conservativo. Básicamente, si el dominio del campo es una región “simplemente conectada” entonces la condición de iguadad de las derivadas cruzadas es suficiente para garantizar que el campo sea conservativo.
Una región \(\Omega\) se considera simplemente conectada, o simplemente conexa, cuando el interior de cualquier curva cerrada incluida en \(\Omega\) está completamente contenido en \(\Omega\). De una manera intuitiva, una región simplemente conectada es una región sin “agujeros”.
En particular, si un campo vectorial es diferenciable y está definido en todos los puntos de \(R^2\), entonces si
el campo será conservativo.
Teniendo en cuenta el concepto de rotacional de un campo vectorial en el plano que se introdujo al presentar los campos basados en operadores diferenciales, la condición para que el campo sea conservativo es
En el caso de un campo de velocidades, el rotacional permite medir la componente de rotación del movimiento; en el caso de campos de fuerzas el rotacional está relacionado con la componente de torsión.
Aunque en las afirmaciones anteriores se han planteado para el caso de campos en el plano, podrían generalizarse también para campos en el espacio.
Condición necesaria y suficiente para ser campo conservativo:
Dado un campo vectorial \(\vec{F}\) definido sobre una región simplemente conectada \(\Omega\), una condición necesaria y suficiente para que sea conservativo es que
En el caso de campos tridimensionales, y de acuerdo a la definición de rotacional, para que el campo sea conservativo se debería cumplir:
El hecho de ser conservativo implica también la existencia de una función potencial, de manera que el campo se convierte en el campo gradiente de dicha función potencial y podría aplicarse el teorema fundamental del cálculo integral de línea. Así la circulación entre dos puntos sería la diferencia de los valores de la función potencial en esos dos puntos.
Ejemplo:
Dado el campo \(\vec{F}=yz\vec{i}+xz\vec{j}+xy\vec{k}\), y la curva \(C\) definida por la parametrización \(\vec{r}(t)=(t^3,t^2,t)\) con \(t\in[0,1]\). La integral de línea del campo sobre la curva es:
La integral podría haberse resuelto también observando que el campo es conservativo, ya que \(rot\,\vec{F}=\vec{0}\), y que una función potencial del campo es
y entonces
Todos estos cálculos pueden comprobarse fácilmente con ayuda de Python
F = S.y*S.z*S.i + S.x*S.z*S.j + S.x*S.y*S.k
vec.is_conservative(F)
True
vec.scalar_potential(F, S)
inicio = S.origin.locate_new('', 0*S.i)
final = S.origin.locate_new('', S.i + S.j + S.k)
vec.scalar_potential_difference(F, S, inicio, final)
La integral también podría ser calculada directamente, comprobando que coincide con la diferencia de potenciales. En este caso, al ser una curva tridimensional no puede definirse un objeto Curve
from sympy.vector import ParametricRegion
C = ParametricRegion((t**3, t**2, t), (t, 0, 1))
vec.vector_integrate(F, C)
Una vez entendida la importancia de disponer de funciones potenciales en los campos conservativos y de disponer de un test rápido para comprobar si un campo es conservativo o no, el siguiente paso es saber encontrar esas funciones potenciales.
Con la ayuda de Python el proceso es sencillo, pero también es interesante saber cómo es el proceso de obtención de esas funciones. En el siguiente ejemplo se muestra un sencillo método para encontrar las funciones potenciales \(f(x,y)\) de un campo \(\vec{F}\), basado en exigir que \(\nabla f=\vec{F}\) y resolver el sistema de ecuaciones en derivadas parciales resultante.
Ejemplo:
El campo \(\vec{F}(x,y)=(2xy+3y^2+2)\vec{i}+(x^2+6xy+3)\vec{j}\) está definido y es diferenciable en todo \(R^2\), además cumple la condición
por tanto es un campo conservativo. Si \(f(x,y)\) es una función potencial de dicho campo, entonces se debería cumplir \(\vec{F}=\nabla f\), es decir:
Integrando la primera de la ecuaciones anteriores con respecto a la variable \(x\), se obtendría:
donde \(c(y)\) sería una función dependiente solo de la variable \(y\). Llevando esta expresión a la segunda ecuación se obtendría una nueva ecuación que permite obtener la estructura de la función \(c(y)\):
de donde \(c(y)=3y+c\) siendo \(c\) una constante arbitraria. En definitiva, las funciones potenciales del campo \(\vec{F}\) serían de la forma
Se comprueban estos cálculos con ayuda de Python:
F = (2*S.x*S.y + 3*S.y**2 + 2)*S.i + (S.x**2 + 6*S.x*S.y +3)*S.j
vec.is_conservative(F)
True
vec.scalar_potential(F, S)
Ejercicios propuestos#
Comprobar que el campo vectorial \(\vec{F}(x,y)=2xy\vec{i}+(x^2+3y^2)\vec{j}\) es conservativo y calcular una función potencial correspondiente.
Determinar una función \(h(y)\) con \(h(0)=0\) que haga que el siguiente campo vectorial sea conservativo. Hallar además la circulación de \(\vec{F}\) sobre una curva arbitraria que una el punto \((0,0)\) con el \((1,2)\).
Demostrar que la integral \(\int_{(1,0)}^{(2,1)} (2xy-y^4+3)dx+(x^2-4xy^3)dy\) es independiente del camino seguido para ir del punto \((1,0)\) al punto \((2,1)\). Calcular además su valor
Dado el campo \(\vec{F}(x,y)=(10x^4-2xy^3)\vec{i}+(-3x^2y^2)\vec{j}\), calcular la integral del campo para ir del punto \((0,0)\) al punto \((2,1)\) a lo largo de la curva \(x^4-6xy^3=4y^2\). Comprobar previamente si es conservativo.
De un campo de fuerzas se sabe que en cada punto del plano la fuerza está dirigida hacia el origen de coordenadas y su magnitud es proporcional a la distancia al origen.
¿Es un campo conservativo? En caso afirmativo calcular su función potencial.
Calcular el trabajo que realiza el campo al desplazar una partícula sobre la elipse \(\frac{x^2}{a^2}+\frac{y^2}{b^2}=1\) en el primer cuadrante y en sentido antihorario.
Calcular la integral \(\int_C x^2\,dx+2x\,dy+z^2\,dz\) donde \(C\) es la curva, recorrida en sentido positivo, definida por
Comprobar que el siguiente campo vectorial tridimensional es conservativo y calcular una función potencial