Ecuaciones lineales de primer orden#

Un tipo especial de ecuación que aparece en muchos modelos prácticos es el correspondiente a las ecuaciones lineales de primer orden.

Ecuaciones lineales de primer orden:

Se dice que una ecuación diferencial de primer orden es lineal cuando puede expresarse en la forma

\[\frac{dy}{dx}+p(x)y=q(x)\]

Cuando \(q(x)=0\) se dice que la ecuación es homogénea.

Realmente las ecuaciones lineales homogéneas son separables, y se puede comprobar que la solución general sería

\[y=Ce^{-\int p(x)dx}\]

En el caso de la ecuación general no homogénea, se puede transformar en una expresión directamente integrable si se multiplican ambos miembros de la ecuación por

\[e^{\int p(x)dx}\]

Obteniéndose como solución general de la ecuación lineal la expresión

\[y=e^{-\int p(x)dx}\left( \int q(x)e^{\int p(x)dx}dx+C \right) \]

siendo \(C\) una constante arbitraria.

Ejemplo:

La ecuación

\[\frac{dy}{dx}-y=3e^{2x}\]

es una ecuación lineal con \(p(x)=-1\) y \(q(x)=3e^{2x}\). Su solución general puede ser obtenida directamente aplicando la fórmula anterior, para ello se debe calcular en primer lugar

\[\int p(x)dx=\int -dx=-x\]

En este paso puede prescindirse de las constantes de integración ya que estarán todas incluidas en la constante final \(C\) que aparecerá en la solución general.

Una vez calculada esta primera integral, la solución general de la ecuación será:

\[y=e^{-\int p(x)dx}\left( \int q(x)e^{\int p(x)dx}dx+C \right) =e^x\left( \int 3e^{2x}e^{-x}dx+C \right) =e^x(3e^x+C) \]

Es decir, la solución general de la ecuación lineal considerada es \(y=3e^{2x}+C e^x\) con \(C\) constante arbitraria.

La comprobación con Python es la siguiente:

import sympy as sp
x = sp.Symbol('x')
y = sp.Function('y')
ecuacion = sp.Eq(y(x).diff(x)-y(x), 3*sp.exp(2*x))
sp.dsolve(ecuacion)
\[\displaystyle y{\left(x \right)} = \left(C_{1} + 3 e^{x}\right) e^{x}\]

Ejemplo (enfriamiento de un cuerpo):

Un cuerpo que tiene una temperatura de 90ºC es depositado (en el tiempo \(t=0\)) en un lugar donde la temperatura se mantiene a 20ºC. Después de 3 minutos, la temperatura ha disminuido a 60ºC. Nos podríamos plantear algunas preguntas importantes:

  • ¿Cual es la temperatura del cuerpo después de 5 minutos?

  • ¿Cuánto tiempo debe pasar para que el cuerpo tenga 40ºC?

El enfriamiento de un cuerpo se rige por la ley de enfriamiento de Newton, que establece que la velocidad de enfriamiento de un cuerpo es proporcional a la diferencia de temperaturas entre él y el medio que lo rodea.

La velocidad de enfriamiento es el ritmo con el que cambia la temperatura con respecto al tiempo, es decir, \(\frac{dT}{dt}\), asumiendo que \(T(t)\) es la función que mide la temperatura en el instante de tiempo \(t\). Teniendo en cuenta esto, la ecuación diferencial que rige el proceso de enfriamiento es

\[\frac{dT}{dt}=k(T-T_a)\]

donde \(T_a\) es la temperatura del medio que rodea al cuerpo, y que se supone constante. Se trata de una ecuación lineal que podría resolverse aplicando la fórmula de la solución general vista anteriormente.

Teniendo en cuanta la temperatura inicial del cuerpo, el problema de valor inicial que debe resolverse en primera instancia es:

\[\begin{split} \left\{ \begin{array}{l} \frac{dT}{dt}=k(T-20)\\ T(0)=90 \end{array} \right. \end{split}\]

La resolución del problema con Python sería la siguiente:

t, k = sp.symbols('t,k')
T = sp.Function('T')
ecuacion = sp.Eq(T(t).diff(t), k*(T(t) - 20))
condicion = {T(0):90}
solucion = sp.dsolve(ecuacion, ics=condicion)
solucion
\[\displaystyle T{\left(t \right)} = 70 e^{k t} + 20\]

Para determinar el valor de la constante de proporcionalidad (\(k\)) puede usarse la otra condición que se conoce

\[T(3)=60\]
solucion.subs(t,3).subs({T(3):60})
\[\displaystyle 60 = 70 e^{3 k} + 20\]
sp.solve(solucion.subs(t,3).subs({T(3):60}), k)

[log(14**(2/3)/7) - 2*I*pi/3, log(14**(2/3)/7) + 2*I*pi/3, log(14**(2/3)/7)]

Como puede observarse, la ecuación algebraica tiene tres soluciones, siendo las dos primeras números complejos, por lo que se debe utilizar únicamente la tercera solución

sp.solve(solucion.subs(t,3).subs({T(3):60}), k)[2].evalf()
\[\displaystyle -0.186538595978474\]

Ahora que ya se dispone de todos los datos para definir una función numérica que determine la temperatura del cuerpo en cada instante \(t\):

import numpy as np
def Temperatura(tiempo): return(70*np.exp(-0.1865*tiempo)+20)

En el instante \(t=5\) la temperatura sería

Temperatura(5)

47.549799063442265

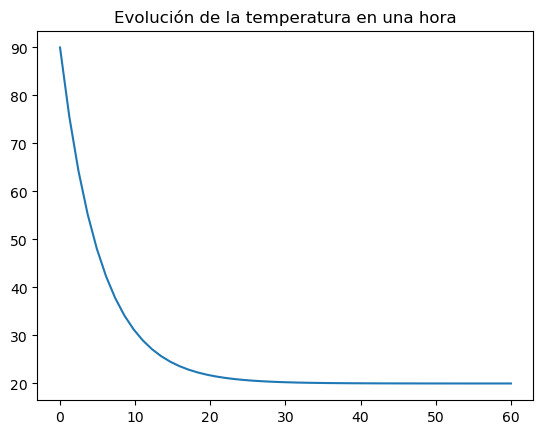
import matplotlib.pyplot as plt
tiempo = np.linspace(0,60)
plt.title('Evolución de la temperatura en una hora')
plt.plot(tiempo, Temperatura(tiempo))
plt.show()
_images/0801f5b844538861f2cf33f54a0ceb97cc7f3819e1ab88d10591e56b7a7a686b.png

Para determinar el tiempo necesario para que la temperatura del cuerpe llegue a 40ºC se debería resolver la ecuación \(Temperatura(t)=40\), pero al estar la función Temperatura definida como numérica, la ecuación algebraica no puede resolverse con las funciones del paquete SymPy. Una opción es utilizar la función fsolve() que ofrece el paquete de cálculo científico SciPy y que permite aproximar raíces de ecuaciones.

from scipy.optimize import fsolve
def ecuacion(t): return Temperatura(t) - 40
fsolve(ecuacion, 0)

array([6.71722771])

Temperatura(6.71722771)

40.000000011607355

Algunas ecuaciones diferenciales no son lineales pero sí que resultan fácilmente transformables en lineales con algún cambio de variable. A continuación se analizan dos de estos tipos de ecuaciones que se pueden convertir en lineales.

Ecuación de Bernoulli#

Ecuación de Bernoulli:

Se llama ecuación de Bernoulli a la que se puede expresar en la forma

\[\frac{dy}{dx}=P(x)y+Q(x)y^n\]

siendo \(n\) un número real. Si \(n=0\) o \(n=1\) la ecuación de Bernoulli es directamente lineal, por lo que se puede asumir que \(n\neq 0\) y \(n\neq 1\). La ecuación de Bernoulli se transforma directamente en lineal con el cambio de variable:

\[u=y^{-n+1}\]

Antes de aplicar el cambio debe dividirse a ambos lados de la ecuación por \(y^n\).

Ejemplo:

La ecuación

\[y'=y^2-y\]

es una ecuación de Bernoulli con \(n=2\). Dividiendo por \(y^2\) a ambos lados de la ecuación se obtiene

\[y'y^{-2}=1-y^{-1}\]

A continuación se aplicaría el cambio \(u=y^{-n+1}=y^{-1}\), con lo que \(u'=-y^{-2}y'\). Se obtendría de esta manera una ecuación lineal de primer orden:

\[-u'=1-u \Leftrightarrow u'-u=-1\]

Esta ecuación podría resolverse directamente con la fórmula de resolución de las ecuaciones lineales

\[u=e^{-\int p(x)dx}\left(\int q(x)e^{\int p(x)dx}dx+C\right)\]

siendo en este caso \(p(x)=-1\) y \(q(x)=-1\). En definitiva:

\[=e^{-\int -dx}\left(\int -e^{\int -dx}dx+C\right)= e^x\left(-\int e^{-x}dx+C\right)=e^x\left(e^{-x}+C\right)=1+Ce^{x}\]

Deshaciendo el cambio se obtiene la solución de la ecuación original:

\[y^{-1}=1+Ce^{x} \Rightarrow y=\frac{1}{1+Ce^{x}}\]

En Python la resolución simbólica de este tipo de ecuaciones también es posible:

x = sp.Symbol('x')
y = sp.Function('y')
ecuacion = sp.Eq(y(x).diff(x), y(x)**2-y(x))
sp.dsolve(ecuacion)
\[\displaystyle y{\left(x \right)} = \frac{C_{1}}{C_{1} - e^{x}}\]

Ecuación de Riccati#

Otro tipo de ecuaciones que puede ser reducida a lineal es la conocida como ecuación de Riccati. Esta ecuación es de la forma

\[y'=P(x)y^2+Q(x)y+R(x)\]

Esta ecuación puede reducirse a una ecuación lineal si se conoce una solución particular \(y_p\) y se hace el cambio

\[y=y_p+\frac{1}{u}\]

Ejemplo:

Para resolver la ecuación

\[y'=y^2-(2x+1)y+x^2+x+1\]

se necesita conocer una solución particular. Puede comprobarse que \(y_p=x\) es una solución de la ecuación, entonces se realiza el cambio

\[y=x+\frac{1}{u}\]

y se obtiene la ecuación

\[1-\frac{u'}{u^2}=(x+\frac{1}{u})^2-(2x+1)(x+\frac{1}{u})+x^2+x+1\]

Simplificando la ecuación anterior se llega a una ecuación lineal

\[u'-u=-1\]

cuya solución general es \(u=1+Ce^x\). Deshaciendo el cambio se obtiene la solución general de la ecuación inicial:

\[y=x+\frac{1}{1+Ce^x}\]

De nuevo, se comprueba con Python el resultado obtenido:

ecuacion = sp.Eq(y(x).diff(x), y(x)**2-(2*x+1)*y(x)+x**2+x+1)
sp.dsolve(ecuacion)
\[\displaystyle y{\left(x \right)} = \frac{C_{1} x + C_{1} - x e^{x}}{C_{1} - e^{x}}\]

Ejercicios propuestos#

  • Resolver las siguientes ecuaciones lineales

\[\frac{dy}{dx}+\frac{2y}{x}=2\cos x\]
\[y=x(y'-x\cos x)\]
\[y(x^2+x)+x^2y'=0\]

  • Resolver el siguiente problema de valor inicial

\[\begin{split}\left\{ \begin{array}{l} \frac{dy}{dx}-\frac{4}{x}y=x^5 e^x\\ y(1)=2 \end{array} \right.\end{split}\]

  • Comprobar que la ecuación \(y'+P(x)y=Q(x)y\log y\) con \(P(x)\) y \(Q(x)\) funciones reales, se transforma en una ecuación lineal haciendo el cambio \(u=\log y\).

  • Resolver las siguientes ecuaciones de Bernoulli:

\[y'+\frac{y}{x}=\frac{\log x}{x}y^2\]
\[3xy'-2y=\frac{x^3}{y^2}\]
\[y'=y^4\cos x+y\tan x\]

  • Resolver las siguientes ecuaciones de Riccati

\[y'+2ye^x-y^2=e^{2x}+e^x\]
\[y'-2xy+y^2=5-x^2\]
\[3y'+y^2+\frac{2}{x^2}=0\]