Teorema de Green y sus aplicaciones#

En esta sección se estudiará un importante resultado que relaciona cierto tipo de integrales de línea de campos vectoriales con las integrales dobles. Se trata de un resultado de gran aplicabilidad práctica y que permite simplificar el cálculo de algunas integrales de campos.

Antes de introducir ese resultado, se presenta una nueva notación que se utilizará para hacer referencia a integrales de campo sobre curvas cerradas. Dado un campo vectorial \(\vec{F}\) y una curva cerrada \(C\), la integral del campo a lo largo de la curva \(C\) se denotará como

\[\oint\limits_C \vec{F}\circ d\vec{r}\]

Es importante destacar que esta notación solo se utiliza para hacer referencia a integrales sobre curvas cerradas.

Introducida esta notación, el teorema de Green establece una relación entre la integral de campo sobre una curva cerrada y la integral doble de su rotacional.

Teorema de Green:

Dada una curva \(C\) cerrada simple, de clase \(C^1\) a trozos y de orientación positiva (recorrida en sentido contrario a las agujas del reloj), sea \(D\) la región del plano que queda encerrada por \(C\), y \(\vec{F}=M\vec{i}+N\vec{j}\) un campo vectorial definido y diferenciable en todo \(R\), entonces

\[\oint\limits_C \vec{F}\circ d\vec{r} = \iint\limits_D rot\,\vec{F}\;dA\]

es decir

\[\oint\limits_C Mdx+Ndy =\iint\limits_D \left( \frac{\partial N}{\partial x}-\frac{\partial M}{\partial y} \right)dA \]

De nuevo, conviene puntualizar que este resultado solo es válido para curvas cerradas, recorridas en sentido positivo y de clase \(C^1\) a trozos, y siempre que el campo esté definido y sea diferenciable en toda la región que delimita la curva.

\[\;\]

Como caso particular, en los campos conservativos el rotacional es nulo, y por tanto

\[\oint\limits_C \vec{F}\circ d\vec{r}=0\;\;\mbox{ si }\vec{F}\mbox{ es conservativo}\]

El teorema de Green también permite establecer que si el campo \(\vec{F}\) está definido y es diferenciable en todo \(R^2\) y su rotacional es nulo en todos los puntos, entonces el campo es necesariamente conservativo.

El teorema de Green permite además simplificar el calculo de determinadas integrales, tal como se pone de manifiesto en el siguiente ejemplo.

Ejemplo:

Considérese la integral de línea

\[\oint\limits_C (3y+\sqrt{x^2+1})dx+(5x-e^{y^2})dy\]

donde \(C\) es la circunferencia \(x^2+y^2=4\) recorrida en sentido positivo. Evidentemente, la circunferencia es una curva regular cerrada, y el campo integral está definido y es diferenciable en todo \(R^2\), y en particular lo será dentro del círculo \(D\) limitado por \(C\).

Las funciones que determinan el campo son

\[M(x,y)=3y+\sqrt{x^2+1};\;\;\;N(x,y)=5x-e^{y^2}\]

y su rotacional

\[rot\,\vec{F}=\frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}=5-3=2\]

Por tanto, haciendo uso de la igualdad que establece el teorema de Green, la integral buscada será:

\[\oint\limits_C (3y+\sqrt{x^2+1})dx+(5x-e^{y^2})dy=\iint\limits_D 2\,dA=2\iint\limits_R \,dA=2\,area(R)=8\pi\]

A continuación se comprueba con Python cómo la integral de línea toma ese mismo valor. Sin embargo, la integral resultante es bastante compleja y no puede realizarse de forma simbólica, debe recurrirse a una aproximación numérica de la integral.

import sympy as sp
import sympy.vector as vec
from sympy.geometry import Curve

# establecimiento del sistema de coordenadas
S = vec.CoordSys3D('')
# definición del campo
F = (3*S.y + sp.sqrt(S.x**2+1))*S.i + (5*S.x - sp.exp(S.y**2))*S.j
# definición de las curva
x,y = sp.symbols('x,y')
circunferencia = vec.ImplicitRegion((x, y), x**2+y**2-4)
# cálculo de la integral de línea
vec.vector_integrate(F, circunferencia)
\[\displaystyle - 2 \int\limits_{0}^{2 \pi} 6\, dt - 2 \int\limits_{0}^{2 \pi} \left(- \sqrt{4 \sin^{2}{\left(t \right)} + 1} \cos{\left(t \right)}\right)\, dt - 2 \int\limits_{0}^{2 \pi} e^{4} e^{- 4 \sin^{2}{\left(t \right)}} \sin{\left(t \right)}\, dt - 2 \int\limits_{0}^{2 \pi} \left(- 16 \sin^{2}{\left(t \right)}\right)\, dt\]

Al no poder realizarse la integración simbólica, lo que sí que se puede realizar simbólicamente es el cálculo de la función a integrar \(\vec{F}(\vec{r}(t))\circ \vec{r}\,'(t)\)

t = sp.symbols('t')
x, y = 2*sp.cos(t), 2*sp.sin(t)
Ft = (3*y + sp.sqrt(x**2+1))*S.i + (5*x - sp.exp(y**2))*S.j
velocidad = sp.diff(x,t)*S.i + sp.diff(y,t)*S.j
integrando = Ft.dot(velocidad)
integrando
\[\displaystyle - 2 \left(\sqrt{4 \cos^{2}{\left(t \right)} + 1} + 6 \sin{\left(t \right)}\right) \sin{\left(t \right)} + 2 \left(- e^{4 \sin^{2}{\left(t \right)}} + 10 \cos{\left(t \right)}\right) \cos{\left(t \right)}\]

Utilizando la función print() sobre ese resultado se puede obtener una expresión más apropiada para su uso en la definición numérica de la función

print(integrando)

-2*(sqrt(4*cos(t)**2 + 1) + 6*sin(t))*sin(t) + 2*(-exp(4*sin(t)**2) + 10*cos(t))*cos(t)

import numpy as np
fn = lambda t: -2*(np.sqrt(4*np.cos(t)**2 + 1) + 6*np.sin(t))*np.sin(t) + 2*(-np.exp(4*np.sin(t)**2) + 10*np.cos(t))*np.cos(t)

El último paso es la integración numérica con la función quad() del módulo de integración del paquete SciPy

from scipy import integrate
integrate.quad(fn, 0, 2*np.pi)

(25.13274122871834, 2.3394578542966504e-07)

El resultado es una muy buena aproximación del valor \(8\pi\) que se obtuvo con la integral doble

8*np.pi

25.132741228718345

El teorema de Green admite una generalización, para el caso de recintos de integración un poco más complejos.

Teorema de Green generalizado:

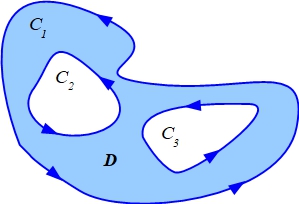
Si \(C_1,C_2,\dots,C_n\) son curvas cerradas simples, de clase \(C^1\) a trozos y de orientación positiva, de manera que \(C_2,\dots,C_n\) están contenidas en el interior de \(C_1\) y tienen intersección vacía dos a dos, se define \(D\) como la región interior de \(C_1\) una vez eliminados los interiores de \(C_2,\dots,C_n\). Entonces si \(\vec{F}=M\vec{i}+N\vec{j}\) es un campo vectorial definido y diferenciable en todo \(R\), se cumple

\[\oint\limits_{C_1}\vec{F}\circ d\vec{r} -\sum_{k=2}^n \oint\limits_{C_k}\vec{F}\circ d\vec{r} = \iint\limits_D rot\,\vec{F}\;dA\]

El tipo de curvas y regiones que se consideran en esta generalización del teorema de Green es el que se muestra en la siguiente figura.

Aplicaciones del teorema de Green#

Cálculo de áreas de recintos limitados por curvas#

El teorema de Green, además de permitir simplificar el cálculo de determinadas integrales curvilíneas, puede ser utilizado para calcular áreas de recintos delimitados por curvas cerradas.

Dada una región \(D\) delimitada por una curva \(C\) cerrada simple, de clase \(C^1\) a trozos y de orientación positiva, entonces se puede calcular el área de \(D\) por cualquiera de las siguientes expresiones:

\[ area(D) = \oint\limits_C xdy \]
\[ area(D) = -\oint\limits_C ydx \]
\[ area(D) = \frac{1}{2}\oint\limits_C xdy-ydx \]

Por ejemplo, en el caso de la primera expresión, si se considera un campo con \(M(x,y)=0\) y \(N(x,y)=x\), su rotacional es

\[rot\,\vec{F} = \frac{\partial N}{\partial x}-\frac{\partial M}{\partial y}=1\]

y de acuerdo al teorema de Green:

\[\oint\limits_C xdy = \iint\limits_R dA=area(R)\]

Ejemplo:

Para calcular el área de una elipse de centro \((0,0)\) y semiejes \(a\) y \(b\), se podría proceder de la siguiente manera.

En primer lugar se necesita una parametrización de la curva

\[\vec{r}(t)=(a\cos t, b\sin t)\mbox{ con }t\in[0,2\pi]\]

Para a continuación calcular la integral

\[\oint\limits_C xdy =\int_0^{2\pi} a\cos t\,b\cos t\,dt =ab\int_0^{2\pi}\cos^2t\,dt\]

Teniendo en cuenta la relación \(\cos^2t=\frac{1}{2}(1+\cos 2t)\), el área de la elipse resulta

\[area=\frac{ab}{2}\int_0^{2\pi}(1+\cos 2t)dt=ab\pi\]

De manera equivalente, el área podría haberse calculado con la integral

\[area=\frac{1}{2}\oint\limits_C xdy-ydx=\frac{1}{2}\int_0^{2\pi}ab\cos^2t\,dt+ab\sin^2t\,dt=ab\pi\]

Se comprueba que las tres integrales de linea anteriores calculan todas ellas el área de la elipse

t,a,b = sp.symbols('t,a,b')
x,y = a*sp.cos(t), b*sp.sin(t)
sp.integrate(x*sp.diff(y,t), (t,0,2*sp.pi))
\[\displaystyle \pi a b\]
sp.integrate(-y*sp.diff(x,t), (t,0,2*sp.pi))
\[\displaystyle \pi a b\]
(1/2)*sp.integrate(x*sp.diff(y,t)-y*sp.diff(x,t), (t,0,2*sp.pi))
\[\displaystyle 1.0 \pi a b\]

Flujo de un campo a través de una curva cerrada#

Otra de las aplicaciones del teorema de Green es el cálculo de flujos de campos vectoriales a través de curvas cerradas. El flujo de un campo vectorial \(\vec{F}\) a través de una curva \(C\) se define como

\[\int_C \vec{F}\circ\hat{n}\,ds\]

donde \(\hat{n}\) es el vector unitario normal a la curva. El producto escalar \(\vec{F}\circ\hat{n}\) representa entonces la componente de la fuerza perpendicular a la curva.

Dado un campo representando, por ejemplo, las velocidades de un fluido, el flujo es una medida de la cantidad de fluido que atraviesa la curva por unidad de tiempo, entendiéndose como flujo positivo el que atraviesa a la curva de izquierda a derecha según el sentido de recorrido, y negativo el que lo atraviesa de derecha a izquierda.

Teniendo en cuenta que \(d\vec{r}=(dx,dy)=\hat{T}\,ds\), siendo \(\hat{T}\) el vector unitario tangente a la curva, y siendo \(\hat{n}\) perpendicular a \(\hat{T}\), se tendría que \(\hat{n}\,ds=(dy,-dx)\). En definitiva, dado un campo vectorial \(\vec{F}=P\vec{i}+Q\vec{j}\), el flujo se calcularía mediante la integral

\[\int_C \vec{F}\circ\hat{n}\,ds = \int_C -Qdx+Pdy\]

Aplicando el teorema de Green con \(M=-Q\) y \(N=P\), se obtendría, que en el caso de una curva cerrada, recorrida en sentido positivo, el flujo del campo sobre la curva vendría dado por

\[Flujo=\oint\limits_C \vec{F}\circ\hat{n}\,ds =\iint\limits_D div\vec{F}\,dA\]

siendo \(D\) la región delimitada por la curva \(C\), y \(div\vec{F}\) la divergencia del campo vectorial, es decir

\[div\vec{F}=\frac{\partial P}{\partial x}+\frac{\partial Q}{\partial y}\]

De nuevo, esto solamente sería válido para el caso de curvas cerradas.

Ejemplo:

Dado el campo \(\vec{F}(x,y)=x\vec{i}+y\vec{j}\) y \(C\) la curva cerrada formada por la circunferencia de centro el origen y radio \(a\). La divergencia del campo sería:

\[div\vec{F}=\frac{\partial}{\partial x}(x)+\frac{\partial}{\partial y}(y)=2\]

y por tanto el flujo del campo a través de la circunferencia

\[Flujo_{\vec{F}}= \iint\limits_R 2 dA = 2\,area(R)=2\pi a^2\]

Si en lugar de considerar el campo \(\vec{F}\) se considera un nuevo campo \(\vec{G}(x,y)=-y\vec{i}+x\vec{j}\), la divergencia en este caso sería

\[div\vec{G}=\frac{\partial}{\partial x}(-y)+\frac{\partial}{\partial y}(x)=0\]

y por tanto el flujo sería nulo:

\[Flujo_{\vec{G}}= \iint\limits_R 0\,dA = 0\]

A continuación va a realizarse una representación gráfica de ambos campos vectoriales en el caso \(a=1\), con la que podrá apreciarse con claridad la diferencia entre ambos casos a la hora de computar el flujo del campo a través de la circunferencia. En el segundo caso ese flujo es nulo, debido a la tangencia entre el campo y la curva.

import matplotlib.pyplot as plt

x,y = np.meshgrid(np.linspace(-1,1,10),np.linspace(-1,1,10))
t = np.linspace(0,2*np.pi)
rx, ry = np.cos(t), np.sin(t)
fig, ax = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(10, 4))
ax[0].set_title('Flujo del campo (x,y)')
ax[0].axis('equal')
ax[0].quiver(x,y,x,y)
ax[0].plot(rx,ry, linewidth=4)
ax[1].set_title('Flujo del campo (-y,x)')
ax[1].axis('equal')
ax[1].quiver(x,y,-y,x)
ax[1].plot(rx,ry, linewidth=4)
plt.show()
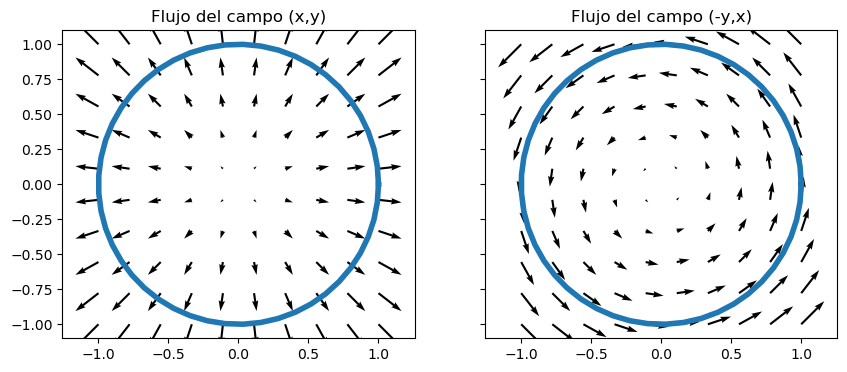
_images/da9568d36ef33f20c522f72f49f8a3e0a6b09b98fa020432aed9025c6762c6f0.png

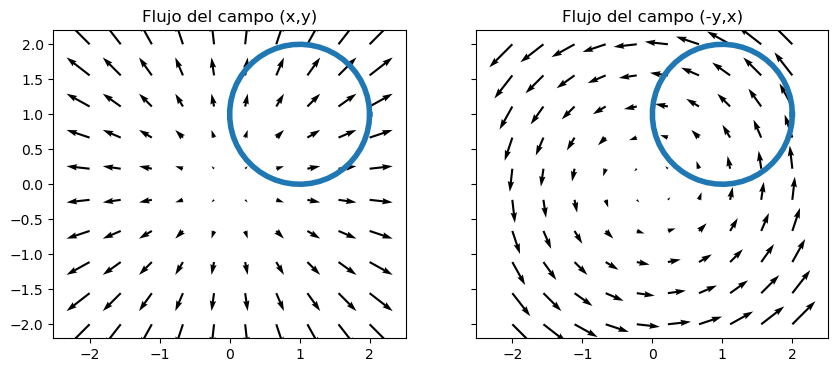
Como puede comprobarse, en el cálculo de las integrales anteriores, el centro de la circunferencia que define la curva \(C\) no influye en el valor del flujo. Por ejemplo, a continuación se realiza una representación gráfica del flujo situando el centro de la circunferencia en el punto \((1,1)\).

Aparentemente los flujos parecen diferentes, pero sin embargo debe tenerse en cuenta que en esta nueva situación unos flujos son de salida de la curva (positivos) y otros de entrada (negativos), por lo que se compensan unos con otros y el flujo global seguirá siendo el mismo que en el caso de la circunferencia centrada en el origen.

x,y = np.meshgrid(np.linspace(-2,2,10),np.linspace(-2,2,10))
t = np.linspace(0,2*np.pi)
rx, ry = 1+np.cos(t), 1+np.sin(t)
fig, ax = plt.subplots(nrows=1, ncols=2, sharey=True, figsize=(10, 4))
ax[0].set_title('Flujo del campo (x,y)')
ax[0].axis('equal')
ax[0].quiver(x,y,x,y)
ax[0].plot(rx,ry, linewidth=4)
ax[1].set_title('Flujo del campo (-y,x)')
ax[1].axis('equal')
ax[1].quiver(x,y,-y,x)
ax[1].plot(rx,ry, linewidth=4)
plt.show()
_images/5a3378d699f7b7097a51aca0b3a1f6f62b65e327ea8afe59e314ea5bea061f8a.png

Ejercicios propuestos#

  • Comprobar el Teorema de Green sobre el cuadrado de vértices \((0, 0)\), \((2, 0)\), \((2, 2)\) y \((0, 2)\) con el campo vectorial \(\vec{F}(x,y)=(x^2-xy^3)\vec{i}+(y^2-2xy)\vec{j}\).

  • Utilizando el teorema de Green, calcular el trabajo realizado por el campo de fuerzas \(\vec{F}(x,y)=(y+3x)\vec{i}+(2y-x)\vec{j}\) al mover una partícula a lo largo de la frontera de la elipse \(4x^2+y^2=4\).

  • Calcular la siguiente integral de línea sobre la frontera \(C\) del conjunto \(R=[0,1]\times[0,1]\)

\[\oint\limits_C (5-xy-y^2)dx+(x^2-2xy)dy\]

  • Utilizar el teorema de Green para calcular el área del cuadrilátero determinado por los puntos \((0,0)\), \((5,1)\), \((4,5)\) y \((0,3)\).

  • Determinar todas las circunferencias \(C\) del plano para las cuales se cumple

\[\oint\limits_C y^2dx+x^2dy=0\]