Superficies en el espacio

Además de curvas, en el espacio se pueden considerar superficies. De una forma intuitiva se puede ver una superficie como un subconjunto de \(R^3\) que tiene dos dimensiones, pero la definición rigurosa de este concepto exige la consideración de representaciones paramétricas. A diferencia de lo que ocurre con las curvas, en las superficies se necesitan dos parámetros para su definición.

Superficie parametrizada:

Dado un conjunto conexo \(\Omega\subseteq R^2\) una superficie parametrizada es una aplicación continua

\[\begin{split}\begin{array}{rl} \vec{s}:\Omega &\longrightarrow R^3\\ (u,v) &\longrightarrow \vec{s}(u,v)=(s_1(u,v),s_2(u,v),s_3(u,v)) \end{array}\end{split}\]

Las ecuaciones paramétricas de la superficie serán, por tanto

\[\begin{split}\begin{array}{l} x=s_1(u,v)\\ y=s_2(u,v)\\ z=s_3(u,v) \end{array}\end{split}\]

Al igual que ocurría en el caso de las curvas, una misma superficie puede tener diferentes parametrizaciones equivalentes. Existen determinadas propiedades de la superficie que son invariantes por la parametrización.

Los puntos de una superficie parametrizada también verifican una ecuación del tipo

\[g(x,y,z)=0\]

Esta ecuación se denomina ecuación cartesiana implícita de la superficie, aunque no siempre es fácil de deducirla a partir de la parametrización de la superficie.

---

Ejemplo:

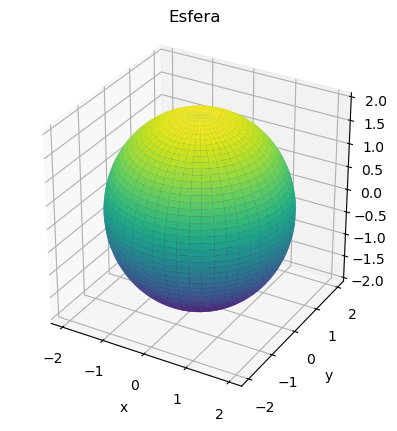
Las ecuaciones

\[\begin{split}\begin{array}{l} x=R\cos\theta\sin\phi\\ y=R\sin\theta\sin\phi\\ z=R\cos\phi \end{array}\end{split}\]

con \((\theta,\phi)\in[0,2\pi]\times[0,\pi]\) corresponden a una esfera centrada en el origen y de radio \(R\).

La ecuación cartesiana implícita de esta esfera es

\[x^2+y^2+z^2=R^2\]

Con ayuda del paquete Matplotlib de Python resulta sencillo representar superficies parametrizadas. Por ejemplo, la esfera podría representarse usando el siguiente código:

import matplotlib.pyplot as plt 
import numpy as np
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Esfera')
ax.set_xlabel('x'); ax.set_ylabel('y')
theta, phi = np.meshgrid(np.linspace(0,2*np.pi), np.linspace(0,np.pi))
R = 2
x = R * np.cos(theta) * np.sin(phi)
y = R * np.sin(theta) * np.sin(phi)
z = R * np.cos(phi)
ax.plot_surface(x, y, z, cmap='viridis')
ax.set_box_aspect([1, 1, 1])
plt.show()

---

Ejemplo:

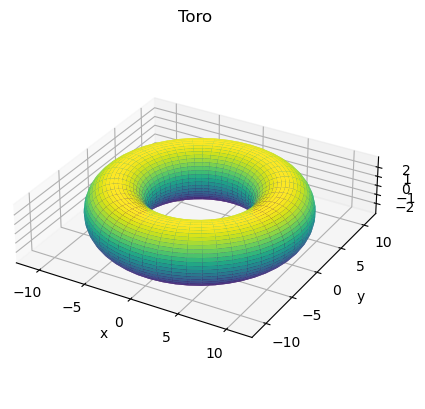
En este nuevo ejemplo se muestra la superficie toriodal, también conocida como toro.

Esta superficie puede parametrizarse de la siguiente manera:

\[x = (R+r\cos\theta)\cos\phi\]

\[y = (R+r\cos\theta)\sin\phi\]

\[z = r\sin\theta\]

con \(\theta\) y \(\phi\) variando en el intervalo \([0,2\pi]\). \(R\) y \(r\) son los dos radios que determinan el toro.

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Toro')
ax.set_xlabel('x'); ax.set_ylabel('y');
phi, theta = np.meshgrid(np.linspace(0,2*np.pi), np.linspace(0,2*np.pi))
r, R = 3, 8
x = (R + r * np.cos(theta)) * np.cos(phi)
y = (R + r * np.cos(theta)) * np.sin(phi)
z = r * np.sin(theta)
ax.plot_surface(x, y, z, cmap='viridis')
ax.set_box_aspect([1, 1, 0.25])
plt.show()

---

Ejemplo:

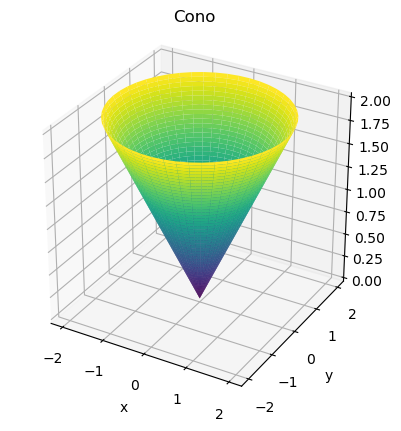
Un cono tiene como ecuación implícita

\[x^2+y^2=z^2\]

Si se producen cortes del cono con planos de la forma \(z=t\) se obtendrían circunferencias centradas en el origen y de radio \(t\), por lo que una parametrización del cono podría ser:

\[\vec{s}(\alpha, t) = (t\cos\alpha, t\sin\alpha, t)\]

es decir

\[x = t\cos\alpha\]

\[y = t\sin\alpha\]

\[z = t\]

donde \(\alpha\in[0,2\pi]\), \(t\in[0,H]\) siendo \(H\) la altura del cono

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Cono')
ax.set_xlabel('x'); ax.set_ylabel('y');
H = 2
alpha, t = np.meshgrid(np.linspace(0,2*np.pi), np.linspace(0,H))
x = t * np.cos(alpha)
y = t * np.sin(alpha)
z = t
ax.plot_surface(x, y, z, cmap='viridis')
ax.set_box_aspect([1, 1, 1])
plt.show()

---

A continuación se analizan presentan las parametrizaciones de algunas superficies especiales:

• Plano: un plano en el espacio viene determinado por un punto \((x_0,y_0,z_0)\) y dos vectores \(\vec{v}=(v_1,v_2,v_3)\) y \(\vec{w}=(w_1,w_2,w_3)\). Unas ecuaciones paramétricas de dicho plano serían:

\[\begin{split}\begin{array}{l} x=x_0+\lambda v_1+\mu w_1\\ y=y_0+\lambda v_2+\mu w_2\\ z=z_0+\lambda v_3+\mu w_3 \end{array}\;\;\;\;\mbox{ con }\lambda,\mu\in R\end{split}\]

y la ecuación cartesiana implícita

\[(x-x_0,y-y_0,z-z_0)\cdot(\vec{v}\times\vec{w})=0\]

o equivalentemente

\[\begin{split}\left| \begin{array}{ccc} x-x_0 & y-y_0 & z-z_0 \\ v_1 & v_2 & v_3 \\ w_1 & w_2 & w_3 \\ \end{array} \right|=0\end{split}\]

• Superficie definida en forma cartesiana explícita: dada la superficie de ecuación \(z=f(x,y)\), se puede parametrizar en la forma

\[\begin{split}\begin{array}{l} x=u\\ y=v\\ z=f(u,v) \end{array}\;\;\;\;\mbox{ con }(u,v)\in D_f\end{split}\]

• Elipsoide: la ecuación general de un elipsoide de centro \((x_0,y_0,z_0)\) y ejes paralelos a los ejes coordenados es

\[\frac{(x-x_0)^2}{a^2}+\frac{(y-y_0)^2}{b^2}+\frac{(z-z_0)^2}{c^2}=1\]

y su parametrización

\[\begin{split}\begin{array}{l} x=x_0 + a\cos u\sin v\\ y=y_0 + b\sin u\sin v\\ z=z_0 + c\cos v \end{array}\;\;\;\;\mbox{ con }(u,v)\in [0,2\pi]\times[0,\pi]\end{split}\]

• Superficie cilíndrica: si se considera una curva en el plano con parametrización \((x,y)=(\alpha(t),\beta(t))\) con \(t\in[a,b]\), la superficie cilíndrica con generatriz paralela al eje \(OZ\) viene dada por la parametrización

\[\begin{split}\begin{array}{l} x=\alpha(t)\\ y=\beta(t)\\ z=v \end{array}\;\;\;\;\mbox{ con }t\in [a,b], v\in R\end{split}\]

---

Ejemplo:

El plano que pasa por los puntos \((2,1,0)\), \((1,3,1)\) y \((3,2,5)\) podría parametrizarse de la siguiente manera.

En primer lugar, se podrían construir dos vectores directores:

\[\vec{v}=(1,3,1)-(2,1,0)=(-1,2,1)\]

\[\vec{w}=(3,2,5)-(2,1,0)=(1,1,5)\]

Con esos dos vectores y el primero de los puntos se construye la parametrización

\[(x,y,z)=(2,1,0)+\lambda(-1,2,1)+\mu(1,1,5)=(2-\lambda+\mu, 1+2\lambda+\mu, \lambda+5\mu)\]

donde \(\lambda\) y \(\mu\) tomarían valores libremente.

Si, por ejemplo se considera \(\lambda,\mu\in[0,1]\) se estaría considerando la parte del plano que se muestra a continuación:

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Superficie en un plano')
ax.set_xlabel('x'); ax.set_ylabel('y');
l, m = np.meshgrid(np.linspace(0,1), np.linspace(0,1))
x, y, z = 2-l+m, 1+2*l+m, l+5*m
ax.plot_surface(x, y, z, cmap='viridis')
ax.set_box_aspect([1, 1, 1])
plt.show()

---

Ejemplo:

Un caso particular de superficie es aquella que puede expresarse de manera explícita \(z=f(x,y)\), en ese caso la superficie corresponde con la representación gráfica de la funcion \(f(x,y)\). Por ejemplo, a continuación se representa la superficie definida por

\[z=\sin(\sqrt{x^2+y^2})\]

con \((x,y)\in[-5,5]\times[-5,5]\)

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Superficie explícita')
ax.set_xlabel('x'); ax.set_ylabel('y');
x, y = np.meshgrid(np.linspace(-5,5), np.linspace(-5,5))
z = np.sin(np.sqrt(x**2+y**2))
ax.plot_surface(x, y, z, cmap='viridis')
ax.set_box_aspect([1, 1, 1])
plt.show()

---

Ejemplo:

Suponiendo que en el plano se considera la curva \(x^2+y^2=1\) (circunferencia centrada en el origen y de radio 1) y que se permite que la variable \(z\) tome valores libremente en el intervalo \([0,5]\), el cilindro que se genera vendría parametrizado por:

\[\begin{split}\begin{array}{l} x=\cos t\\ y=\sin\ t\\ z= v \end{array}\;\;\;\;\mbox{ con }t\in [0,2\pi], v\in[0,5]\end{split}\]

y su representación gráfica sería la siguiente:

fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Cilindro')
ax.set_xlabel('x'); ax.set_ylabel('y');
t, v = np.meshgrid(np.linspace(0,2*np.pi), np.linspace(0,5))
x = np.cos(t)
y = np.sin(t)
z = v
ax.plot_surface(x, y, z, cmap='viridis')
ax.set_box_aspect([1, 1, 1])
plt.show()

Superficies regulares y vectores normales

Superficie regular:

Dada una superficie definida por una parametrización \(\vec{s}(u,v)=(s_1(u,v),s_2(u,v),s_3(u,v))\) y un punto \((x_0,y_0,z_0)=\vec{s}(u_0,v_0)\) de la superficie, se dice que el punto es regular cuando los vectores \(\frac{\partial \vec{s}}{\partial u}(u_0,v_0)\) y \(\frac{\partial \vec{s}}{\partial v}(u_0,v_0)\) son linealmente independientes, es decir cuando

\[\frac{\partial \vec{s}}{\partial u}(u_0,v_0)\times \frac{\partial \vec{s}}{\partial v}(u_0,v_0)\neq \vec{0}\]

Se dice que la superficie es regular cuando todos su puntos son regulares.

Un caso particular de superficie regular es las definidas explícitamente \(z=f(x,y)\). En tales superficies \(\vec{s}(u,v)=(u,v,f(u,v))\) y por tanto:

\[\frac{\partial \vec{s}}{\partial u}\times \frac{\partial \vec{s}}{\partial v}= (1,0,\frac{\partial f}{\partial u})\times (0,1,\frac{\partial f}{\partial v}) =(-\frac{\partial f}{\partial u},-\frac{\partial f}{\partial v},1)\neq\vec{0}\]

El módulo de cálculo vectorial simbólico de SymPy dispone de un método cross que aplicado sobre un vector permite calcular el producto vectorial con otro. Por ejemplo, a continuación se hace uso del paquete \(SymPy\) para comprobar que una esfera tiene algún punto que no es regular.

---

Ejemplo: Las ecuaciones

\[\begin{split}\begin{array}{l} x=\cos\theta\sin\phi\\ y=\sin\theta\sin\phi\\ z=\cos\phi \end{array}\end{split}\]

con \((\theta,\phi)\in[0,2\pi]\times[0,\pi]\) corresponden a una esfera centrada en el origen y de radio 1. Se comprueba que se trata de una superficie regular:

import sympy as sp
import sympy.vector as vec
# establecimiento del sistema de coordenadas
S = vec.CoordSys3D('')
# parametrización de la esfera
theta, phi = sp.symbols('theta,phi')
x = sp.cos(theta) * sp.sin(phi)
y = sp.sin(theta) * sp.sin(phi)
z = sp.cos(phi)

v1 = sp.diff(x,theta)*S.i + sp.diff(y,theta)*S.j + sp.diff(z,theta)*S.k
v2 = sp.diff(x,phi)*S.i + sp.diff(y,phi)*S.j + sp.diff(z,phi)*S.k
v1.cross(v2)

\[\displaystyle (- \sin^{2}{\left(\phi \right)} \cos{\left(\theta \right)})\mathbf{\hat{i}_{}} + (- \sin^{2}{\left(\phi \right)} \sin{\left(\theta \right)})\mathbf{\hat{j}_{}} + (- \sin{\left(\phi \right)} \sin^{2}{\left(\theta \right)} \cos{\left(\phi \right)} - \sin{\left(\phi \right)} \cos{\left(\phi \right)} \cos^{2}{\left(\theta \right)})\mathbf{\hat{k}_{}}\]

v1.cross(v2).simplify()

\[\displaystyle (- \sin^{2}{\left(\phi \right)} \cos{\left(\theta \right)})\mathbf{\hat{i}_{}} + (- \sin^{2}{\left(\phi \right)} \sin{\left(\theta \right)})\mathbf{\hat{j}_{}} + (- \frac{\sin{\left(2 \phi \right)}}{2})\mathbf{\hat{k}_{}}\]

Este vector sería nulo en aquellos puntos correspondientes a ángulos con \(\sin\phi=0\), es decir \(\phi=0\) o \(\phi=\pi\). Estos puntos corresponderían a los dos polos de la esfera.

---

Si el punto \((x_0,y_0,z_0)\) es un punto regular de la superficie, entonces los vectores \(\frac{\partial \vec{s}}{\partial u}(u_0,v_0)\) y \(\frac{\partial \vec{s}}{\partial v}(u_0,v_0)\) junto con el punto determinan el plano tangente a la superficie en dicho punto. Por tanto, las ecuaciones paramétricas del plano tangente son:

\[(x,y,z)=(x_0,y_0,z_0)+\lambda\frac{\partial \vec{s}}{\partial u}(u_0,v_0)+\mu \frac{\partial \vec{s}}{\partial v}(u_0,v_0)\]

y la ecuación cartesiana

\[(x-x_0,y-y_0,z-z_0)\cdot\left(\frac{\partial \vec{s}}{\partial u}(u_0,v_0)\times \frac{\partial \vec{s}}{\partial v}(u_0,v_0)\right)=0\]

En el caso de que la superficie esté definida mediante una ecuación cartesiana \(g(x,y,z)=0\), siendo \(g(x,y,z)\) una función de clase \(C^1\), el vector \(\nabla g(x_0,y_0,z_0)\) es perpendicular a la superficie, es decir, a su plano tangente, en el punto \((x_0,y_0,z_0)\) y por tanto la ecuación del plano tangente a la superficie sería, en este caso

\[ \frac{\partial g}{\partial x}(x_0,y_0,z_0)(x-x_0)+ \frac{\partial g}{\partial y}(x_0,y_0,z_0)(y-y_0)+ \frac{\partial g}{\partial z}(x_0,y_0,z_0)(z-z_0)=0 \]

Si el punto \((x_0,y_0,z_0)\) es un punto regular de la superficie, entonces, como se ha comentado los vectores \(\frac{\partial \vec{s}}{\partial u}(u_0,v_0)\) y \(\frac{\partial \vec{s}}{\partial v}(u_0,v_0)\) serían linealmente independientes, y además junto con el punto \((x_0,y_0,z_0)\) determinan el plano tangente a la superficie en dicho punto. Teniendo en cuenta eso, los dos productos vectoriales

\[ \frac{\partial \vec{s}}{\partial u}(u_0,v_0)\times \frac{\partial \vec{s}}{\partial v}(u_0,v_0) \]

y

\[ \frac{\partial \vec{s}}{\partial v}(u_0,v_0)\times \frac{\partial \vec{s}}{\partial u}(u_0,v_0) \]

son vectores normales a la superficie. Además ambos vectores son iguales en módulo y dirección pero de sentidos opuestos. La elección de uno u otro vector como vector normal induce una orientación en la superficie.

---

Ejemplo:

Se analizan a continuación las dos posibles orientaciones de un cilindro \(x^2+y^2=1\).

En primer lugar, la parametrización es:

\[\vec{s}(u,v)=(\cos u, \sin u, v)\]

Los dos vectores normales son

\[\begin{split} \frac{\partial \vec{s}}{\partial u}\times\frac{\partial \vec{s}}{\partial v} =\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ -\sin u & \cos u & 0 \\ 0 & 0 & 1 \\ \end{array}\right|=\cos u\vec{i} + \sin u\vec{j} \end{split}\]

y

\[\begin{split} \frac{\partial \vec{s}}{\partial v}\times\frac{\partial \vec{s}}{\partial u} =\left|\begin{array}{ccc} \vec{i} & \vec{j} & \vec{k} \\ 0 & 0 & 1 \\ -\sin u & \cos u & 0 \\ \end{array}\right|=-\cos u\vec{i} - \sin u\vec{j} \end{split}\]

Las orientaciones que determinan esos vectores normales son las que se muestran en las siguientes imágenes.

# Superficie
u, v = np.meshgrid(np.linspace(0,2*np.pi), np.linspace(0,5))
x, y, z = np.cos(u), np.sin(u), v

# Vectores normales
uu, vv = np.meshgrid(np.linspace(0,2*np.pi,12), np.linspace(0,5,12))
xx, yy, zz = np.cos(uu), np.sin(uu), vv
cx, cy, cz = np.cos(uu), np.sin(uu), 0

# Gráfica la superficie y los vectores normales
fig, ax = plt.subplots(nrows=1, ncols=2, subplot_kw={"projection":"3d"})
ax[0].set_title('Orientación (cos u, sin u, 0)')
ax[0].plot_surface(x, y, z, cmap='viridis', alpha=0.8)
ax[0].quiver(xx, yy, zz, cx, cy, cz, color='blue', alpha=0.2, length=0.3)
ax[0].set_box_aspect([1, 1, 1])
ax[1].set_title('Orientación (-cos u, -sin u, 0)')
ax[1].plot_surface(x, y, z, cmap='viridis', alpha=0.8)
ax[1].quiver(xx, yy, zz, -cx, -cy, -cz, color='blue', length=0.3)
ax[1].set_box_aspect([1, 1, 1])
plt.show()

---

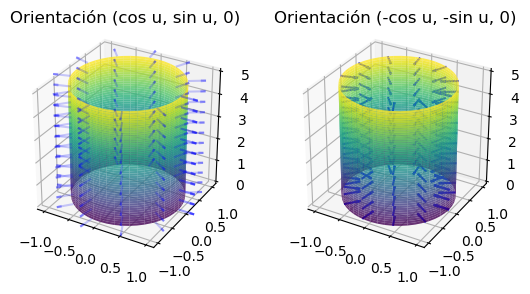
Dado un punto de la superficie, existen dos vectores normales unitarios, con la misma dirección pero sentidos opuestos. Como ya se ha comentado, elegir uno de esos sentidos implica dar una orientación a la superficie. Orientar una superficie puede verse como elegir una de las “caras” de la superficie, ahora bien, no todas las superficies tienen dos caras, es decir, no toda superficie es orientable. Un ejemplo clásico de superficie no orientable es la conocida como banda de Moebius, que viene definida por la parametrización

\[ x(s,t) = (R+s\cos(t/2))\cos(t) \]

\[ y(s,t) = (R+s\cos(t/2))\sin(t) \]

\[ z(s,t) = s\sin(t/2) \]

con \(s\in[-w,w]\) y \(t\in[0,2\pi]\), siendo \(R\) el radio y \(2w\) la anchura de la banda. A continuación se representa esta superficie para comprobar que realmente no tiene dos caras.

w, R = 1, 5
s, t = np.meshgrid(np.linspace(-w,w), np.linspace(0,2*np.pi))
x = (R + s*np.cos(t/2))*np.cos(t)
y = (R + s*np.cos(t/2))*np.sin(t)
z = s*np.sin(t/2)
fig, ax = plt.subplots(subplot_kw={"projection":"3d"})
ax.set_title('Banda de Moebius')
ax.plot_surface(x, y, z, cmap='viridis')
ax.set_box_aspect([1, 1, 0.5])
plt.show()

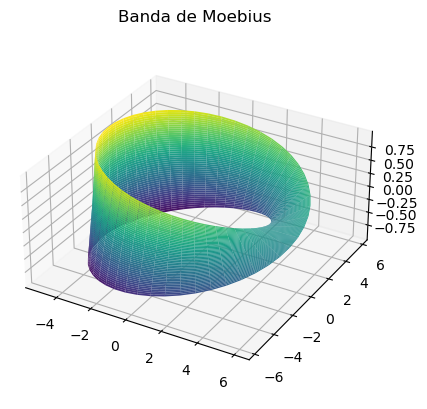
La superficie es orientable cuando el vector normal es continuo sobre la superficie. Esto significa que al moverse a lo largo de una curva cerrada dentro de la superficie, al llegar al punto de partida el sentido del vector normal es el mismo que el que tenía en el inicio. Eso no ocurre en la banda de Moebius, por lo que no es una superficie orientable.

Ejercicios propuestos

• Dada la superficie cilíndrica \(x^2+y^2=r^2\), obtener una parametrización e identificar cuáles son sus puntos regulares.

• Dada la superficie definida por \(z=x^2+2xy^3-y\), obtener una parametrización y comprobar si el punto \((1,1,2)\) de la superficie es regular. En caso de que lo sea calcular la ecuación cartesiana del plano tangente a la superficie en dicho punto y la recta normal.

• Encontrar una parametrización del plano que pasa por los puntos \((0,1,-2)\), \((1,3,-1)\) y \((0,2,0)\) e identificar los vectores normales a la superficie.

• Comprobar que en una superficie definida por una ecuación en forma explícita \(z=f(x,y)\) con \((x,y)\in\Omega\) todos sus puntos son regulares. Calcular además la ecuación del plano tangente a la superficie en un punto \((x_0,y_0,f(x_0,y_0))\).

• Calcular la ecuación del plano tangente y de la recta normal a la superficie \(\vec{s}(u,v)=(u-v,u+v,uv)\) en el punto \(P=(1,3,2)\).

• Calcular el plano tangente a la esfera de radio 2 y centro \(c=(1, 2, 3)\) en el punto \(P=(3, 2, 3)\).

• Calcular el plano tangente en el punto \(P=(1,0,1)\) de la superficie que viene parametrizada por \(\vec{s}(u,v)=(u\cos v,u\sin v, u)\) con \(u\in R\) y \(v\in[0,2\pi)\).